🕤 🤳🏽 👨🏿‍✈️ Desarrollo de un convertidor de video 264 a avi para dashcam QCM-08DL 🕴️ 🏷️ 🔍

De hecho, el artículo está dedicado al desarrollo de un programa para reempaquetar video DVR de un contenedor a otro, si se le puede llamar conversión. Aunque, toda mi vida pensé que el convertidor se dedica a convertir (transcodificar) el formato de video. Este artículo es la segunda parte de mi última publicación, donde hablé en detalle sobre el acceso a todas las grabaciones de video del DVR. Pero al comienzo de la publicación, establecí otra tarea: estudiar el algoritmo por el cual funciona el programa estándar 264-avi repacker y crear el mismo programa que realizaría las mismas operaciones, pero no en una, sino en un grupo completo de archivos, además "Un clic".

Explicaré una vez más la esencia de todas las cosas en un lenguaje simple.

El usuario tiene una grabadora de video, por ejemplo, el popular modelo QCM-08DL. Necesita un video para una fecha y hora específicas. Puede eliminarlo en una unidad flash USB o a través de una interfaz web de un DVR a una computadora. El archivo de video extraído (extensión .264) solo se abrirá en el programa del reproductor que viene con el DVR. El jugador está muy incómodo. Todavía puede abrirlo en el reproductor VLC configurando el modo RAW H264 en la configuración de demultiplexación (configuración para usuarios avanzados). Pero al mismo tiempo, aparentemente, los bloques de secuencias de audio, que se interpretan como video y no hay sonido, interfieren con la reproducción normal. Y para abrir el video en cualquier reproductor, el archivo .264 primero debe convertirse a algún formato popular, por ejemplo, avi. También se incluye un programa de conversión con el DVR. Pero ella también está muy incómoda. Cuando se trata de uno o más archivos, no hay problemas. Sin embargo, cuando la tarea es obtener acceso a todos los videos en el disco duro, y aún más para convertirlos a todos en el formato popular, las herramientas estándar prácticamente no son adecuadas.

El problema de acceso a todos los archivos ha sido resuelto. Este fue el tema de la última publicación. Procedemos a resolver el segundo problema. Ya me han dado "consejos prácticos": es suficiente cambiar el nombre de la extensión de "264" a "avi" en el nombre del archivo, y todo saldrá mal, dicen, no hay nada que molestar. Pero este es el error más común de cualquier usuario común, que, por regla general, no comprende los problemas relevantes.

En una publicación anterior, ya escribí brevemente sobre la estructura del archivo fuente .264. Déjame recordarte.

La información principal con transmisiones de audio y video se origina en un desplazamiento de 65.536 bytes. Los bloques de transmisión de video comienzan con un encabezado de 8 bytes "01dcH264" (también encontrado "00dcH264"). Los siguientes 4 bytes describen el tamaño del bloque actual de la transmisión de video en bytes. Después de 4 bytes de ceros (00 00 00 00), comienza el bloque de transmisión de video. Los bloques de transmisión de audio tienen el título "03wb" (aunque, según mis observaciones, el primer carácter del encabezado en algunos casos no era necesariamente "0"). Después: 12 bytes de información que aún no he descubierto. Y comenzando con el byte 17, una secuencia de audio de una longitud fija de 160 bytes. No hay etiquetas al final del archivo.

Voy a comentar sobre lo anterior. Todo lo que es hasta un desplazamiento de 65.536 bytes resultó sin resolver e innecesario. Desde un desplazamiento de 65.536 bytes hasta el primer encabezado de la secuencia, hay un pequeño espacio, cuyo contenido tampoco se resuelve y, además, como lo comprobé, no aparece en el archivo avi de salida después de la conversión por un programa regular.

Cada bloque de la transmisión de video representa un cuadro. El primer carácter en el encabezado de los bloques de la secuencia de video es opcionalmente "0". No entendí su propósito, porque, como descubrí, no es la clave para resolver la tarea. El segundo carácter del encabezado de la transmisión de video puede ser "1" o "0". En el segundo caso, el contenido del bloque de transmisión de video es el llamado marco de referencia. Y en el primer caso, el contenido del bloque de transmisión de video es un cuadro comprimido codificado, que depende del cuadro de referencia. El tamaño del contenido del marco de referencia es significativamente mayor que el tamaño del contenido del subcuadro comprimido. El período de repetición del cuadro de referencia probablemente depende de la configuración de la relación de compresión en el DVR. Pero en mi caso, el período de repetición fue de 1 fotograma / segundo.

El programa regular para reempaquetar video del contenedor "264" al contenedor "avi" dio resultados diferentes con respecto a la velocidad de cuadros. En el caso de los videos que se grabaron en modo de alta resolución (704 * 576), la velocidad de cuadros fue de 20 cuadros / segundo. Y en el caso de baja resolución (352 * 288) - 25 cuadros / seg. Esta información es proporcionada por la utilidad MediaInfo. También indica que el tamaño del video es el mismo en cualquier caso: 720 * 576, y el tamaño de la transmisión de video (esta utilidad informa) es 704 * 576 o 352 * 288. La mayoría de los jugadores se implementan específicamente para el tamaño de la transmisión de video. Sin embargo, conocí a un jugador que mostraba incorrectamente el modo de media pantalla cuando reproducía un archivo 352 * 288. Quería corregir esta falla menor en el repacker regular mirando los bytes de la transmisión de video y sacando información sobre el tamaño del cuadro desde allí. Pero a toda prisa, no pude hacer esto. Lo anterior se muestra en la figura a continuación.

Ahora sobre la velocidad de fotogramas. Como descubrí, el repacker regular no accede a ningún campo de encabezado del contenedor "264". Juzga la velocidad de cuadros calculando la relación del número de bloques de video y secuencias de audio. Y este valor en el cálculo ni siquiera se redondea al valor entero más cercano, como se puede ver en la figura anterior (encerrada en un círculo en verde). Como descubrí, el número de bloques de transmisión de audio por unidad de tiempo es siempre y en todas partes (en cualquier archivo) fijo, es decir, 25 bloques por segundo. Si examina el archivo de video con una frecuencia de 20 cuadros / segundo, entonces el cuadro de referencia (bloque) ocurre cada 19 cuadros comprimidos, y en el caso de 25 cuadros / segundo. - Cada 24 cuadros comprimidos.

Continuamos estudiando la estructura del encabezado de la transmisión de video. Descubrimos los primeros ocho bytes: esta es la etiqueta de la referencia o el cuadro comprimido más la palabra clave "H264". Los siguientes cuatro bytes describen, como descubrí, no el tamaño exacto, sino el tamaño aproximado de los contenidos de la transmisión de video. Un repacker normal arroja todos los bytes de este contenido por completo y luego escribe el tamaño resultante en los campos correspondientes del contenedor avi. Y este valor es diferente del valor especificado en el campo correspondiente del archivo fuente .264.

En parte, adiviné doce bytes de información después del encabezado del bloque de secuencia de audio. En cualquier caso, los elementos clave son los últimos 4 bytes, después de lo cual comienza la secuencia de audio. Estos son dos números de 16 bits que describen los parámetros iniciales del esquema de decodificación iterativa de ADPCM a PCM. La decodificación aumenta el tamaño de la transmisión de audio en 4 veces. Cuando examiné los archivos de antemano, descubrí que el repacker de tiempo completo decodifica el audio, pero deja el contenido del video sin cambios.

Sin un conocimiento profundo, intenté durante mucho tiempo averiguar qué algoritmo de decodificación se usaba en mi caso. Intuitivamente ya adivinó que se aplicó el método de compresión ADPCM. Más precisamente, no intuitivamente, pero con un enfoque competente, basado en el hecho de que el flujo de audio se comprime exactamente 4 veces. Y cuando abro un fragmento en Adobe Audition como RAW en varios formatos (y comparo el mismo fragmento después de reempaquetarlo con un programa normal), ADPCM me dio un resultado de sonido muy similar (pero no preciso). Para analizar el algoritmo de compresión, la información en el sitio wiki.multimedia.cx/index.php/IMA_ADPCM me ayudó. Aquí aprendí sobre los dos parámetros iniciales de decodificación, y luego, usando el "método de empuje", me di cuenta de que estos parámetros iniciales se registraron en 4 bytes antes del inicio de la transmisión de audio. Describiré el funcionamiento del algoritmo y daré una interpretación matemática aproximada (bajo el spoiler).

Detalles del algoritmo de decodificación de ADPCM

Hay una secuencia de muestras

$x_0, x_1, x_2, \ puntos. $$ Además, como ya se mencionó, hay dos parámetros iniciales

$y_0$ y

$s_0$ . Necesita obtener una nueva secuencia de muestra

$y_0, y_1, y_2 \ puntos.$ . Como ya puede adivinar, la primera muestra de salida ya se conoce: coincide con uno de los parámetros iniciales

$y_0$ . Esto es algo más que un "desplazamiento inicial". Vale la pena señalar que las muestras de entrada (fuente) están codificadas en cuatro bits. Para los tipos con signo, los enteros de -8 a 7, inclusive, se incluyen en la codificación. El bit más significativo, de hecho, es responsable del signo del número. Las muestras PCM de salida, que se obtienen después de la decodificación, tienen un formato estándar de 16 bits con signo.

Analizando el código del algoritmo en C, puede ver dos tablas. Se enumeran a continuación.

int ima_index_table[] = { -1, -1, -1, -1, 2, 4, 6, 8 };

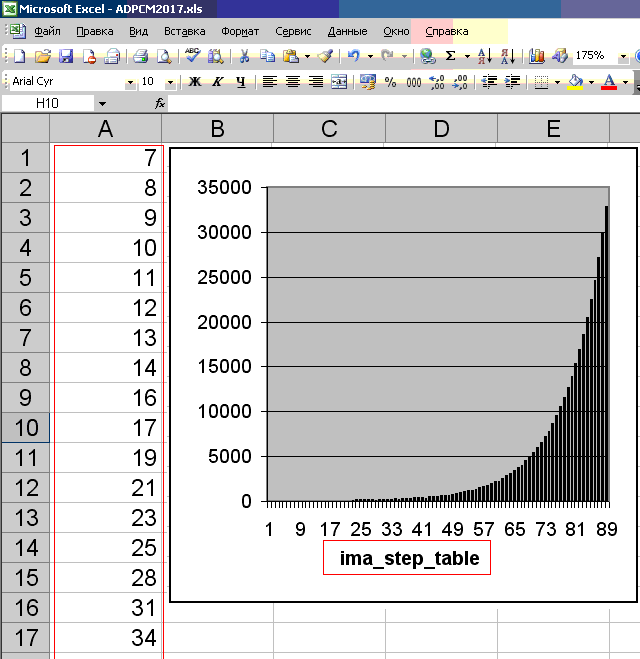
 int ima_step_table[] = { 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 19, 21, 23, 25, 28, 31, 34, 37, 41, 45, 50, 55, 60, 66, 73, 80, 88, 97, 107, 118, 130, 143, 157, 173, 190, 209, 230, 253, 279, 307, 337, 371, 408, 449, 494, 544, 598, 658, 724, 796, 876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066, 2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358, 5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899, 15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767 };

Se puede decir que estos dos conjuntos "mágicos" son funciones tabulares, en cuyos argumentos se sustituyen los mismos dos parámetros iniciales. Durante la iteración, con cada paso, los parámetros se recalculan y sustituyen en estas tablas nuevamente. Primero, veamos cómo se implementa esto en el código.

Declaramos lo necesario, incluidas las variables auxiliares.

 int current1; int step; int stepindex1; int diff; int current; int stepindex; int value; //  ;

Antes de comenzar la iteración, debe asignar el parámetro inicial a la variable actual

$y_0$ , y la variable stepindex es

$s_0$ . Esto se hace fuera del algoritmo en cuestión, por lo que no lo reflejo con el código. Las siguientes son las transformaciones que se realizan en un círculo (en un bucle).

  value = read(input_sample); //   ; current1 = current; stepindex1 = stepindex; step = ima_step_table[stepindex1]; diff = step>>3; if(value & 1){ diff += step >> 2; } if(value & 2){ diff += step >> 1; } if(value & 4){ diff += step; } if(value & 8){ current1 -= diff; if(current1 < -32768){ //,  ""; current1 = -32768; } }else{ current1 += diff; if(current1 > 32767){ //,  ""; current1 = 32767; } } //      :   current1; stepindex1 += ima_index_table[value & 7]; if(stepindex1 < 0){ // ""; stepindex1 = 0; } if(stepindex1 > 88){ // ""; stepindex1 = 88; } output_sample = curent1; //   ; current = current1; stepindex = stepindex1;

En el paso de la variable auxiliar de la matriz ima_step_table, se escribe el valor en el índice stepindex1. Para la primera iteración, este es el parámetro inicial

$s_0$ , para futuras iteraciones, este es un parámetro recalculado

$s_i$ . Luego, el valor de esta matriz se divide por 8 (aparentemente, completamente) por la operación del desplazamiento de bits a la derecha, y la variable diff se inicializa como resultado de esta división. Luego, se analizan los tres bits menos significativos del valor de la muestra de entrada y, según sus estados, la variable diff se puede ajustar en tres términos. Los términos son una división entera similar del valor diff por 4 (>> 2), 2 (>> 1) o diff sin cambios (dejemos que sea una división por 1 para generalización). Luego, se analiza el bit más significativo (con signo) del valor de la muestra de entrada. Dependiendo de su estado, la variable diff que se generó antes de esto se agrega o resta a la variable current1. Este será el valor de la muestra de salida. Para la corrección, los valores están limitados a la parte superior e inferior. Luego, stepindex1 se ajusta agregando el valor de la matriz ima_index_table por el índice del valor de la muestra de entrada con el bit de signo restablecido a cero. Los valores de Stepindex1 también están sujetos a un límite. Al final, antes de repetir este algoritmo, a los valores actuales y stepindex se les asignan los valores recuentos de current1 y stepindex1, y el algoritmo se repite nuevamente.

Puede intentar resolverlo para comprender aproximadamente cómo se forma la variable diff. Dejar

$f_i = f (s_i)$ . Estos son los valores de la variable de paso en cada i-ésimo paso de la iteración, como los valores de la función (matriz) del argumento

$s_i$ donde

$i = 0, 1, 2, \ puntos$ . Por conveniencia, denotamos la variable diff como

$d$ . Siguiendo la lógica del razonamiento descrito anteriormente, tenemos:

$d_i = \ frac {f_i} {8} + x ^ {(0)} _ i \ frac {f_i} {4} + x ^ {(1)} _ i \ frac {f_i} {2} + x ^ {( 2)} _ if_i,$

donde

$x_i ^ {(0)}, x_i ^ {(1)}, x_i ^ {(2)}$ - bajo 3 bits de un número

$x_i$ . Llevando a un denominador común, transformamos esta expresión a una forma más conveniente:

$d_i = \ frac {f_i} 8 \ Bigg (1 + 2x_i ^ {(0)} + 4x_i ^ {(1)} + 8x_i ^ {(2)} \ Bigg) =$

$= \ frac {f_i} 8 \ Bigg (1 + 2 \ Big (x_i ^ {(0)} + 2x_i ^ {(1)} + 4x_i ^ {(2)} \ Big) \ Bigg) = \ frac { f_i} {8} (2x_i + 1).$

La última conversión se basa en el hecho de que, en cierto sentido, los menos tres bits (0 o 1) de un número

$x_i$ con los coeficientes presentados hay algo más que escribir el valor absoluto de este número, y el bit más significativo del número

$x_i$ coincidirá con el signo de toda la expresión. Además de acuerdo con la fórmula

$y_ {i + 1} = y_i + d_i$

Se calcula un nuevo valor de muestra basado en el anterior. Además, se calcula un nuevo valor variable.

$s$ :

$s_ {i + 1} = s_i + t (| x_i |).$

El módulo en la fórmula indica que la variable

$x_i$ entra en funcionamiento

$t$ excluyendo el bit de signo más significativo, que se refleja en el código. Una función

$t$ Es el valor de la matriz ima_index_table con el índice correspondiente al argumento.

En la descripción de las fórmulas, descuidé las operaciones de restricción arriba y abajo. El esquema iterativo total se parece a esto:

$y_0; \ s_0; \ \ x_0, x_1, x_2, \ dots \;$

$d_i = \ frac {f (s_i)} {8} \ big (2x_i + 1 \ big) \;$

$y_ {i + 1} = y_i + d_i \;$

$s_ {i + 1} = s_i + t (| x_i |) \;$

$i = 0, 1, 2, \ puntos.$

Muy profundamente en la teoría de codificación / decodificación de ADPCM en la que no profundicé. Sin embargo, los valores de la tabla de la matriz ima_step_table (de 89 piezas), a juzgar por su reflejo en el gráfico (ver la figura a continuación), describen la distribución probabilística de las muestras en relación con la línea cero. En la práctica, este suele ser el caso: cuanto más cerca está la muestra de la línea cero, más ocurre. Por lo tanto, ADPCM se basa en un modelo probabilístico y de ninguna manera cualquier conjunto fuente de muestras PCM de 16 bits se puede convertir correctamente en muestras ADPCM de 4 bits. En términos generales, ADPCM es PCM con un paso de cuantificación variable. Simplemente, aparentemente, este gráfico refleja este paso muy variable. Es elegido correctamente, en base a la ley de distribución de datos de audio en la práctica.

Ahora pasemos a describir la estructura del contenedor avi. De hecho, es una estructura jerárquica compleja.

Pero, habiendo simplificado la tarea para un caso especial, presenté la estructura avi en forma lineal. El resultado es este: el archivo avi consta de un encabezado grande, bytes de salto cero (JUNK), un área de secuencias de audio y video (con sus encabezados y tamaños de contenido) y una lista de índices. Este último sirve, en particular, para desplazarse por el video en el reproductor. Sin esta lista, el desplazamiento no funcionará (marcado). Es solo una tabla de contenido, que enumera los nombres clave de los bloques de flujo (que coinciden con los nombres en los encabezados de bloque), los tamaños correspondientes de los contenidos y los valores de los desplazamientos (direcciones) relativos al comienzo del área de flujo.

Ahora puede continuar con el desarrollo del programa. Una descripción específica del problema es la siguiente.

En la raíz de la sección X: hay un directorio "DVR". Este directorio contiene muchos subdirectorios no vacíos (y solo subdirectorios) con nombres que corresponden a ciertas fechas. En cada uno de estos subdirectorios hay muchos archivos con diferentes nombres y la extensión "264". Requerido en la sección Y: cree el directorio "DVR", y en él los mismos subdirectorios que en la sección X:. Rellene cada uno de estos subdirectorios con archivos con los mismos nombres correspondientes, pero con extensiones no "264", sino "avi". Estos archivos avi deben obtenerse de los archivos 264 originales procesándolos, lo que, de una forma u otra, repite el algoritmo de un programa existente. El procesamiento consiste en reempaquetar directamente secuencias de video, reempaquetar con decodificar secuencias de audio y formatear el archivo avi. El programa debe iniciarse desde la línea de comandos de la siguiente manera: "264toavi.exe X: Y:", donde "264toavi.exe" es el nombre del programa, "X:" es la sección de origen, "Y:" es la sección de destino.

De hecho, para simplificar la tarea, fue posible escribir un programa que solo se ocuparía de la conversión (reempaquetado) de un archivo, por lo que son dos días: el nombre del archivo de entrada y el nombre del archivo de salida. Y luego, para implementar solo el reempaquetado grupal, puede escribir un archivo por lotes de comandos (bat) usando otras herramientas, por ejemplo, Excel. Pero implementé un programa completo, muy engorroso. Es poco probable que el código fuente merezca la atención de los lectores. Describiré la estructura del código del programa.

El programa está escrito en C en el entorno de desarrollo Dev-C ++ con elementos WinAPI. El programa implementa tres funciones auxiliares grandes: la función de generar el encabezado avi inicial, la función de decodificar una muestra de audio y la función de escanear el archivo fuente "264" por palabras. En palabras, llamo una porción de 4 bytes. Se ha observado que los tamaños de los encabezados y el contenido de todas las secuencias son múltiplos de cuatro bytes. La función de escaneo puede devolver cinco valores: 0 - si son los 4 bytes habituales del flujo de video para el reempaquetado, 1 - si es el encabezado del bloque del flujo de video del marco de referencia, 2 - si es el título del bloque del flujo del video del marco comprimido, 3 - si es el encabezado del bloque de flujo de audio, 4 - si es Bloque "dañado" para ser ignorado durante el reempaque. Muy, muy raro, pero sucedió. El bloque dañado (como lo llamé) es un encabezado como "\ 0 \ 0 \ 0 \ 0H264", donde "\ 0" es el byte cero. El repacker regular ignora los bloques de este tipo. Por supuesto, el contenido de dicho bloque puede resultar bastante funcional, pero ignoro dichos bloques para acercar mi programa al estándar.

En la función principal, además de organizar directorios, la función de escaneo lee el archivo de entrada. Dependiendo de lo que devolvió esta función, se producen más acciones. Si estos son los encabezados de las transmisiones de video, los encabezados correspondientes se forman en el archivo avi de salida. Allí se les llama de manera diferente: "00db" es el título del bloque del flujo de video del cuadro de referencia, y "00dc" es para el cuadro comprimido. Después de la operación de reempaquetado (reescritura de palabras) antes del nuevo encabezado recién encontrado, se calcula el tamaño del contenido reempaquetado y este valor se escribe en el campo que sigue inmediatamente al encabezado de la secuencia que se acaba de procesar. Si se encuentra un encabezado de flujo de audio durante la exploración, el nombre del encabezado "03wb" se genera en el archivo avi de salida y el flujo de audio se decodifica de ADPCM a PCM en el bucle al mismo tiempo que los contenidos decodificados se escriben en el archivo avi. Junto con todo lo anterior, se registra una breve información (tabla de contenido) en un archivo de índice temporal "index". No podría hacer una función de escaneo, pero escriba todo en la función principal. Pero entonces el programa sería muy engorroso y casi difícil de leer.

Al final de toda la operación, cuando finaliza el archivo de entrada "264", antes de pasar a un nuevo archivo, el programa completa de manera competente todas las operaciones. Primero, se ajustan ciertos campos en el encabezado del archivo avi, cuyos valores dependen del tamaño y la cantidad de secuencias de lectura, y luego el contenido del archivo "índice" temporal se adjunta al archivo avi casi terminado, que luego se elimina. Después de estas operaciones, el archivo avi de salida está listo para reproducir.

Mientras se ejecuta el programa, se realiza una visualización de texto en la línea de comando, que muestra el directorio actual, el archivo, así como el número de bloque de la transmisión de video por marco de referencia y el punto de tiempo correspondiente del video en minutos y segundos. Y si el archivo de entrada no tiene un nombre arbitrario, sino el original (que contiene el número de canal, la fecha y la hora en que comenzó la grabación), se produce una visualización más interactiva basada en la aritmética de fecha y hora.

Al probar y depurar el programa, los principales problemas que tuve al trabajar con la decodificación de sonido. La aritmética simple no funcionaba correctamente si, al declarar variables en la función de decodificación, no escribiera correctamente los tipos. Debido a esto, algunos bloques de transmisiones de audio se rompieron y hubo clics de oído. Algunos campos de encabezado incomprensibles del archivo 264 original que no pude entender resultaron insensibles al resultado. A diferencia de un programa normal, mi programa no arroja el último bloque de flujo incompleto de la operación de reempaque. Aunque, su ausencia no jugará ningún papel práctico. Otro programa regular, a diferencia del mío, deja una pequeña cantidad de "basura" (este es el contenido de la última secuencia) al final del archivo avi después de los índices. Por todo esto, el video se reproduce casi igual. Y el programa realiza el reempaquetado durante el mismo período de tiempo que el programa regular.

En conclusión, daré ilustraciones que demuestran la estructura de la organización de los flujos en el archivo .264 (en el editor hexadecimal WinHex) utilizando uno de los archivos como ejemplo y la apariencia del programa RiffPad con el archivo avi reempaquetado abierto en él. Este programa ha simplificado enormemente el proceso de estudiar la estructura de un archivo avi. Demuestra claramente la estructura jerárquica, muestra el contenido de bytes de cada miembro de la estructura e incluso interpreta inteligentemente el contenido de los encabezados en forma de una lista de parámetros. La imagen, en particular, demuestra el hecho de que el contenido de la transmisión de video se sobrescribe sin cambios.

Desarrollo de un convertidor de video 264 a avi para dashcam QCM-08DL

More articles: