¿Cuánto son los datos para el entrenamiento modelo (no) similar a una muestra de prueba?

Considere un escenario en el que su modelo de aprendizaje automático podría no tener valor.

Hay un dicho: "No compares manzanas con naranjas" . Pero, ¿qué sucede si necesita comparar un conjunto de manzanas con naranjas con otro, pero la distribución de frutas en los dos conjuntos es diferente? ¿Se puede trabajar con datos? ¿Y cómo lo harás?


En casos reales, esta situación es común. Al desarrollar modelos de aprendizaje automático, nos enfrentamos a una situación en la que nuestro modelo funciona bien con un conjunto de entrenamiento, pero la calidad del modelo cae bruscamente en los datos de prueba.

Y esto no se trata de reentrenamiento. Digamos que hemos construido un modelo que da un resultado excelente en la validación cruzada, pero muestra un resultado pobre en la prueba. Entonces, en la muestra de prueba hay información que no tenemos en cuenta.

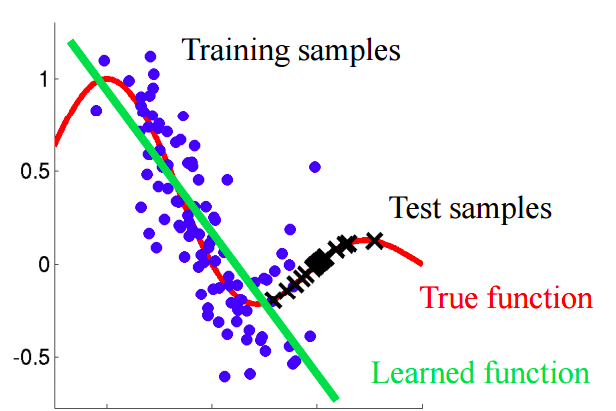
Imagine una situación en la que predecimos el comportamiento del cliente en una tienda. Si las muestras de entrenamiento y prueba se parecen a la imagen a continuación, este es un problema claro:


En este ejemplo, el modelo está entrenado en datos con un valor promedio del atributo "edad del cliente" menor que el valor promedio de un atributo similar en la prueba. En el proceso de aprendizaje, el modelo nunca ha "visto" los valores más grandes del atributo "edad". Si la edad es una característica importante para el modelo, entonces uno no debería esperar buenos resultados en la muestra de prueba.

En este texto, hablaremos sobre enfoques "ingenuos" que nos permiten identificar tales fenómenos y tratar de eliminarlos.

Cambio covariante

Demos una definición más precisa de este concepto. La covarianza se refiere a los valores de las características, y el cambio covariante se refiere a una situación en la que la distribución de los valores de las características en las muestras de entrenamiento y prueba tienen diferentes características (parámetros).

En problemas del mundo real con una gran cantidad de variables, el cambio covariante es difícil de detectar. El artículo discute el método para identificar, así como explicar el cambio covariante en los datos.

Idea principal

Si hay un cambio en los datos, al mezclar las dos muestras, podemos construir un clasificador que pueda determinar si el objeto pertenece a una muestra de entrenamiento o prueba.


Vamos a entender por qué esto es así. Volvamos al ejemplo con los clientes, donde la edad era un signo "desplazado" de las muestras de entrenamiento y prueba. Si tomamos un clasificador (por ejemplo, basado en un bosque aleatorio) y tratamos de dividir la muestra mixta en entrenamiento y prueba, entonces la edad será un signo muy importante para dicha clasificación.

Implementación

Intentemos aplicar la idea descrita a un conjunto de datos real. Use el conjunto de datos de la competencia de Kaggle.

Paso 1: preparación de datos

Primero, seguiremos una serie de pasos estándar: limpiar, completar los espacios en blanco, realizar la codificación de etiquetas para signos categóricos. No se requirió ningún paso para el conjunto de datos en cuestión, por lo tanto, omita su descripción.

import pandas as pd #  train  test train = pd.read_csv('train.csv',low_memory=True) test = pd.read_csv('test.csv',low_memory=True) 

Paso 2: agregar un indicador de fuente de datos

Es necesario agregar un nuevo indicador indicador a ambas partes del conjunto de datos: capacitación y prueba. Para la muestra de entrenamiento con el valor "1", para la prueba, respectivamente, "0".

 #    ,   test,   train test['is_train'] = 0 train['is_train'] = 1 

Paso 3: combinación de las muestras de aprendizaje y prueba

Ahora necesita combinar los dos conjuntos de datos. Dado que el conjunto de datos de entrenamiento contiene una columna de valores objetivo 'objetivo', que no está en el conjunto de datos de prueba, esta columna debe eliminarse.

 #  train, test df_combine = pd.concat([train, test], axis=0, ignore_index=True) #  target df_combine = df_combine.drop('target', axis =1) y = df_combine['is_train'].values #  x = df_combine.drop('is_train', axis=1).values #  tst, trn = test.values, train.values 

Paso 4: compilar y probar el clasificador

Para fines de clasificación, utilizaremos el Clasificador de bosque aleatorio, que configuraremos para predecir las etiquetas de la fuente de datos en el conjunto de datos combinado. Puedes usar cualquier otro clasificador.

 from sklearn.ensemble import RandomForestClassifier import numpy as np rfc = RandomForestClassifier(n_jobs=-1, max_depth=5, min_samples_leaf = 5) predictions = np.zeros(y.shape) #     

Utilizamos una división aleatoria estratificada de 4 pliegues. De esta manera, mantendremos la proporción de las etiquetas 'is_train' en cada pliegue como en la muestra combinada original. Para cada partición, entrenamos al clasificador en la mayoría de la partición y predecimos la etiqueta de clase para la parte diferida más pequeña.

 from sklearn.model_selection import StratifiedKFold, cross_val_score skf = StratifiedKFold(n_splits=4, shuffle=True, random_state=100) for fold, (train_idx, test_idx) in enumerate(skf.split(x, y)): X_train, X_test = x[train_idx], x[test_idx] y_train, y_test = y[train_idx], y[test_idx] rfc.fit(X_train, y_train) probs = rfc.predict_proba(X_test)[:, 1] #   predictions[test_idx] = probs 

Paso 5: interpreta los resultados

Calculamos el valor de la métrica ROC AUC para nuestro clasificador. Con base en este valor, concluimos cuán bien nuestro clasificador revela un cambio covariante en los datos.

Si el clasificador c separa bien los objetos en los conjuntos de datos de entrenamiento y prueba, entonces el valor de la métrica ROC AUC debería ser significativamente mayor que 0.5, idealmente cercano a 1. Esta imagen indica un fuerte cambio covariante en los datos.

Encuentre el valor de ROC AUC:

 from sklearn.metrics import roc_auc_score print('ROC-AUC:', roc_auc_score(y_true=y, y_score=predictions)) # ROC-AUC: 0.49974692698385287 

El valor resultante es cercano a 0.5. Y esto significa que nuestro clasificador de calidad es el mismo que un predictor de etiqueta aleatorio. No hay evidencia de un cambio covariante en los datos.

Dado que el conjunto de datos se toma de Kaggle, el resultado es bastante predecible. Como en otras competencias de aprendizaje automático, los datos se verifican cuidadosamente para garantizar que no haya cambios.

Pero este enfoque se puede aplicar en otros problemas de la ciencia de datos para verificar la presencia de un cambio covariante justo antes del inicio de la solución.

Pasos adicionales

Entonces, o observamos un cambio covariante o no. ¿Qué hacer para mejorar la calidad del modelo en la prueba?

1. Eliminar características sesgadas
2. Usar pesos de importancia de objeto basados ​​en estimaciones de coeficientes de densidad

Eliminar características sesgadas:

Nota: el método es aplicable si hay un cambio covariante en los datos.

• Extraiga la importancia de los atributos del Clasificador de bosque aleatorio, que creamos y capacitamos anteriormente.
• Los signos más importantes son precisamente aquellos que están sesgados y causan un cambio en los datos.
• Comenzando por lo más importante, elimine sobre una base, cree el modelo de destino y observe su calidad. Recoge todos los signos para los que la calidad del modelo no disminuye.
• Descarte las características recopiladas de los datos y cree el modelo final.

Este algoritmo le permite eliminar signos de la canasta roja en el diagrama.

Uso de pesos de importancia de objeto basados ​​en estimaciones de coeficientes de densidad

Nota: el método es aplicable independientemente de si hay un cambio covariante en los datos.

Veamos las predicciones que recibimos en la sección anterior. Para cada objeto, la predicción contiene la probabilidad de que este objeto pertenezca al conjunto de entrenamiento para nuestro clasificador.

 predictions[:10] #array([0.39743827 ... 

Por ejemplo, para el primer objeto, nuestro Clasificador de bosque aleatorio cree que pertenece al conjunto de entrenamiento con una probabilidad de 0.397. Llamar a este valor $$$P (tren)$. O podemos decir que la probabilidad de pertenecer a los datos de prueba es 0.603. Del mismo modo, llamamos probabilidad $$$P (prueba)$.

Ahora un pequeño truco: para cada objeto del conjunto de datos de entrenamiento, calculamos el coeficiente $$$w = \ frac {P (prueba)} {P (tren)}$.

Coeficiente $$$w$nos dice qué tan cerca está un objeto del conjunto de entrenamiento para probar datos. La idea principal:

Podemos usar $$$w$como pesos en cualquiera de los modelos para aumentar el peso de esas observaciones que se parecen a la muestra de prueba. Intuitivamente, esto tiene sentido, ya que nuestro modelo estará más orientado a los datos como en un conjunto de pruebas.

Estos pesos se pueden calcular usando el código:

 import seaborn as sns import matplotlib.pyplot as plt plt.figure(figsize=(20,10)) predictions_train = predictions[:len(trn)] weights = (1./predictions_train) - 1. weights /= np.mean(weights) #  plt.xlabel('  w') plt.ylabel(' ') sns.distplot(weights, kde=False) 

Los coeficientes obtenidos se pueden transferir al modelo, por ejemplo, de la siguiente manera:

 rfc = RandomForestClassifier(n_jobs=-1,max_depth=5) m.fit(X_train, y_train, sample_weight=weights) 

Algunas palabras sobre el histograma resultante:

• Los valores de peso mayores corresponden a observaciones más similares a la muestra de prueba.
• Casi el 70% de los objetos del conjunto de entrenamiento tienen un peso cercano a 1 y, por lo tanto, se encuentran en un subespacio que es similar al conjunto de entrenamiento y al conjunto de prueba. Esto corresponde al valor de AUC que calculamos anteriormente.

Conclusión

Esperamos que esta publicación lo ayude a identificar el "cambio covariante" en los datos y a combatirlo.

Referencias

[1] Shimodaira, H. (2000). Mejora de la inferencia predictiva bajo desplazamiento covariable al ponderar la función de log-verosimilitud. Revista de planificación estadística e inferencia, 90, 227-244.
[2] Bickel, S. y col. (2009) Aprendizaje discriminativo bajo cambio covariable. Journal of Machine Learning Research, 10, 2137–2155
[3] github.com/erlendd/covariate-shift-adaption
[4] Enlace al conjunto de datos utilizado

PD: La computadora portátil con el código del artículo se puede ver aquí .