Richard Hamming: Capítulo 13. Teoría de la información

Lo hicimos!

"El objetivo de este curso es prepararte para tu futuro técnico".

Hola Habr ¿Recuerdas el increíble artículo "Tú y tu trabajo" (+219, 2588 marcado, 429k lecturas)?

Entonces, Hamming (sí, sí, los códigos de Hamming que se autoverifican y corrigen a sí mismos) tiene un libro completo escrito basado en sus conferencias. Lo estamos traduciendo, porque el hombre está hablando de negocios.

Este libro no es solo sobre TI, es un libro sobre el estilo de pensamiento de personas increíblemente geniales. “Esto no es solo una carga de pensamiento positivo; describe condiciones que aumentan las posibilidades de hacer un gran trabajo ".

Gracias por la traducción a Andrei Pakhomov.

La teoría de la información fue desarrollada por C.E. Shannon a fines de la década de 1940. La gerencia de Bell Labs insistió en que lo llamara "teoría de la comunicación", porque Este es un nombre mucho más preciso. Por razones obvias, el nombre "Teoría de la información" tiene un impacto significativamente mayor en el público, por lo que Shannon lo eligió, y es lo que sabemos hasta el día de hoy. El nombre en sí sugiere que la teoría se ocupa de la información, lo que la hace importante, ya que estamos penetrando más profundamente en la era de la información. En este capítulo, abordaré algunas conclusiones básicas de esta teoría, daré evidencia no estricta, sino intuitiva de algunas de las disposiciones separadas de esta teoría, para que comprenda cuál es la "Teoría de la información", dónde puede aplicarla y dónde no .

En primer lugar, ¿qué es "información"? Shannon identifica la información con incertidumbre. Eligió el logaritmo negativo de la probabilidad de un evento como una medida cuantitativa de la información que recibe cuando un evento ocurre con probabilidad p. Por ejemplo, si te digo que el clima en Los Ángeles es brumoso, entonces p está cerca de 1, que en general no nos da mucha información. Pero si digo que llueve en Monterrey en junio, entonces habrá incertidumbre en este mensaje y contendrá más información. Un evento confiable no contiene ninguna información, ya que log 1 = 0.

Detengámonos en esto con más detalle. Shannon creía que una medida cuantitativa de información debería ser una función continua de la probabilidad de un evento p, y para eventos independientes debería ser aditiva: la cantidad de información obtenida como resultado de dos eventos independientes debería ser igual a la cantidad de información obtenida como resultado de un evento conjunto. Por ejemplo, el resultado de una tirada de dados y monedas generalmente se considera como eventos independientes. Traduzcamos lo anterior al lenguaje de las matemáticas. Si I (p) es la cantidad de información contenida en el evento con probabilidad p, entonces para un evento conjunto que consta de dos eventos independientes x con probabilidad p ₁ e y con probabilidad p ₂ obtenemos


(eventos independientes x e y)

Esta es la ecuación funcional de Cauchy, verdadera para todos los p ₁ y p2. Para resolver esta ecuación funcional, suponga que

p ₁ = p ₂ = p,

da



Si p ₁ = p ² y p ₂ = p, entonces



etc. Extendiendo este proceso usando el método estándar para exponenciales para todos los números racionales m / n, lo siguiente es cierto



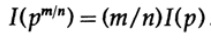
De la supuesta continuidad de la medida de información, se deduce que la función logarítmica es la única solución continua a la ecuación funcional de Cauchy.

En la teoría de la información, es habitual tomar la base del logaritmo de 2, por lo que la elección binaria contiene exactamente 1 bit de información. Por lo tanto, la información se mide por la fórmula



Hagamos una pausa y veamos qué sucedió arriba. En primer lugar, no le dimos una definición al concepto de "información", simplemente definimos una fórmula para su medida cuantitativa.

En segundo lugar, esta medida depende de la incertidumbre y, aunque es lo suficientemente adecuada para máquinas, por ejemplo, sistemas telefónicos, radio, televisión, computadoras, etc., no refleja una actitud humana normal hacia la información.

En tercer lugar, esta es una medida relativa, depende del estado actual de su conocimiento. Si observa el flujo de "números aleatorios" del generador de números aleatorios, asume que cada número siguiente es indefinido, pero si conoce la fórmula para calcular "números aleatorios", se conocerá el siguiente número y, en consecuencia, no contendrá información

Por lo tanto, la definición dada por Shannon para información es en muchos casos adecuada para máquinas, pero no parece corresponder a la comprensión humana de la palabra. Por esta razón, la "Teoría de la información" debe llamarse la "Teoría de la comunicación". Sin embargo, es demasiado tarde para cambiar las definiciones (gracias a las cuales la teoría ha ganado su popularidad inicial, y que todavía hacen que la gente piense que esta teoría trata con la "información"), entonces tenemos que soportarlas, pero hay que Comprenda claramente hasta qué punto la definición de información dada por Shannon está lejos de su sentido común. La información de Shannon trata con algo completamente diferente, a saber, la incertidumbre.

Esto es lo que necesita pensar cuando ofrece alguna terminología. ¿Qué tan consistente es la definición propuesta, por ejemplo, la definición dada por Shannon, con su idea original, y qué tan diferente es? Casi no existe un término que refleje con precisión su visión anterior del concepto, pero al final, es la terminología utilizada la que refleja el significado del concepto, por lo que formalizar algo a través de definiciones claras siempre hace ruido.

Considere un sistema cuyo alfabeto consiste en símbolos q con probabilidades pi. En este caso, la cantidad promedio de información en el sistema (su valor esperado) es:



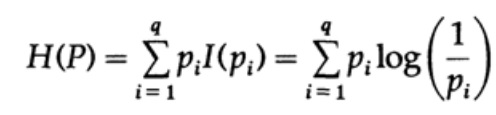
Esto se llama entropía del sistema de distribución de probabilidad {pi}. Usamos el término "entropía" porque la misma forma matemática surge en termodinámica y mecánica estadística. Es por eso que el término "entropía" crea a su alrededor un aura de importancia que, en última instancia, no está justificada. ¡La misma forma matemática de notación no implica la misma interpretación de los caracteres!

La entropía de la distribución de probabilidad juega un papel importante en la teoría de la codificación. La desigualdad de Gibbs para dos distribuciones de probabilidad diferentes pi y qi es una de las consecuencias importantes de esta teoría. Entonces tenemos que demostrar que



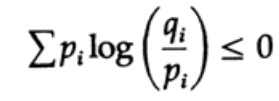
La prueba se basa en un gráfico obvio, la fig. 13.I, que muestra que



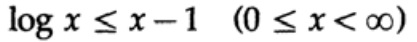
y la igualdad se logra solo para x = 1. Aplicamos la desigualdad a cada sumando de la suma del lado izquierdo:



Si el alfabeto del sistema de comunicación consta de q caracteres, entonces tomando la probabilidad de transmisión de cada carácter qi = 1 / q y sustituyendo q, obtenemos de la desigualdad de Gibbs





Figura 13.I

Esto sugiere que si la probabilidad de transmitir todos los caracteres q es igual e igual a - 1 / q, entonces la entropía máxima es ln q, de lo contrario, la desigualdad se mantiene.

En el caso de un código decodificado de forma única, tenemos la desigualdad de Kraft



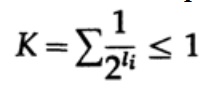
Ahora si definimos pseudo-probabilidades



donde por supuesto = 1, que se deduce de la desigualdad de Gibbs,



y aplicar un poco de álgebra (recuerde que K ≤ 1, por lo que podemos omitir el término logarítmico y posiblemente fortalecer la desigualdad más adelante), obtenemos



donde L es la longitud promedio del código.

Por lo tanto, la entropía es el límite mínimo para cualquier código de caracteres con una palabra de código promedio L. Este es el teorema de Shannon para un canal sin interferencia.

Ahora consideramos el teorema principal sobre las limitaciones de los sistemas de comunicación en los que la información se transmite en forma de un flujo de bits independientes y está presente el ruido. Se supone que la probabilidad de la transmisión correcta de un bit es P> 1/2, y la probabilidad de que el valor del bit se invierta durante la transmisión (se produce un error) es Q = 1 - P. Por conveniencia, suponemos que los errores son independientes y la probabilidad de error es la misma para cada envío bits, es decir, hay "ruido blanco" en el canal de comunicación.

La forma en que tenemos una larga secuencia de n bits codificados en un solo mensaje es una extensión n-dimensional de un código de un bit. Determinaremos el valor de n más tarde. Considere un mensaje que consiste en n-bits como un punto en el espacio n-dimensional. Dado que tenemos un espacio n-dimensional, y por simplicidad asumimos que cada mensaje tiene la misma probabilidad de ocurrencia, hay M mensajes posibles (M también se determinará más adelante), por lo tanto, la probabilidad de cualquier mensaje enviado es igual




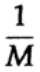
(remitente)
Gráfico 13.II

A continuación, considere la idea del ancho de banda del canal. Sin entrar en detalles, la capacidad del canal se define como la cantidad máxima de información que se puede transmitir de manera confiable a través del canal de comunicación, teniendo en cuenta el uso de la codificación más eficiente. No hay argumento de que se pueda transmitir más información a través del canal de comunicación que su capacidad. Esto se puede probar para un canal simétrico binario (que usamos en nuestro caso). La capacidad del canal para el envío a nivel de bits se establece como



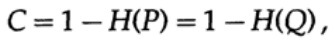
donde, como antes, P es la probabilidad de que no haya ningún error en ningún bit enviado. Al enviar n bits independientes, la capacidad del canal se determina como



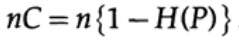
Si estamos cerca del ancho de banda del canal, deberíamos enviar casi tal volumen de información para cada uno de los caracteres ai, i = 1, ..., M. Dado que la probabilidad de aparición de cada carácter ai es 1 / M, obtenemos



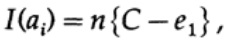
cuando enviamos cualquiera de los mensajes M equiprobables ai, tenemos



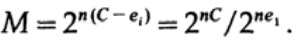
Al enviar n bits, esperamos que ocurran errores nQ. En la práctica, para un mensaje que consiste en n bits, tendremos aproximadamente nQ errores en el mensaje recibido. Para n grande, variación relativa (variación = ancho de distribución,)
la distribución del número de errores será más estrecha al aumentar n.

Entonces, desde el lado del transmisor, tomo el mensaje ai para enviar y dibujo una esfera a su alrededor con un radio



que es ligeramente mayor en una cantidad igual a e2 que el número esperado de errores Q, (Figura 13.II). Si n es lo suficientemente grande, entonces hay una probabilidad arbitrariamente pequeña de la aparición del punto de mensaje bj en el lado del receptor, que va más allá de esta esfera. Dibujaremos la situación, tal como la veo desde el punto de vista del transmisor: tenemos cualquier radio desde el mensaje transmitido ai hasta el mensaje recibido bj con una probabilidad de error igual (o casi igual) a la distribución normal, alcanzando un máximo en nQ. Para cualquier e2 dado, hay n tan grande que la probabilidad de que el punto resultante bj, que va más allá de mi esfera, sea tan pequeña como desee.

Ahora considere la misma situación de su parte (Fig. 13.III). En el lado del receptor hay una esfera S (r) del mismo radio r alrededor del punto recibido bj en el espacio n-dimensional, de modo que si el mensaje recibido bj está dentro de mi esfera, entonces el mensaje ai que envié está dentro de su esfera.

¿Cómo puede ocurrir un error? Se puede producir un error en los casos descritos en la tabla a continuación:



Figura 13.III



Aquí vemos que si en la esfera construida alrededor del punto recibido hay al menos un punto más correspondiente a un posible mensaje no codificado enviado, entonces se produjo un error durante la transmisión, ya que no puede determinar cuál de estos mensajes se transmitió. El mensaje enviado no contiene errores solo si el punto correspondiente está en la esfera, y no hay otros puntos posibles en este código que estén en la misma esfera.

Tenemos una ecuación matemática para la probabilidad de un error Re si se envió ai



Podemos descartar el primer factor en el segundo término, tomándolo como 1. Por lo tanto, obtenemos la desigualdad



Obviamente



por lo tanto



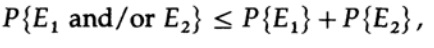
volver a aplicar al último miembro a la derecha



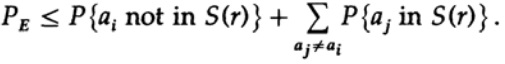
Si n se toma lo suficientemente grande, el primer término se puede tomar arbitrariamente pequeño, digamos, menos de cierto número d. Por lo tanto tenemos



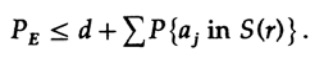
Ahora veamos cómo puede crear un código de reemplazo simple para codificar mensajes M que consisten en n bits. Al no tener idea de cómo construir el código (los códigos de corrección de errores aún no se han inventado), Shannon eligió la codificación aleatoria. Lanza una moneda por cada uno de los n bits en el mensaje y repite el proceso para M mensajes. Todo lo que necesita hacer es lanzar monedas nM, por lo que es posible



diccionarios de código que tienen la misma probabilidad de ½nM. Por supuesto, el proceso aleatorio de crear un libro de códigos significa que hay una probabilidad de duplicados, así como puntos de código, que estarán cerca uno del otro y, por lo tanto, serán una fuente de posibles errores. Es necesario demostrar que si esto no sucede con una probabilidad mayor que cualquier nivel de error pequeño seleccionado, entonces el n dado es lo suficientemente grande.
¡El punto decisivo es que Shannon promedió todos los libros de códigos posibles para encontrar el error promedio! Usaremos el símbolo Av [.] Para denotar el promedio sobre el conjunto de todos los posibles diccionarios de código aleatorio. Promediar sobre la constante d, por supuesto, da una constante, ya que para promediar cada término coincide con cualquier otro término en la suma



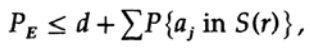
que se puede aumentar (M - 1 va a M)



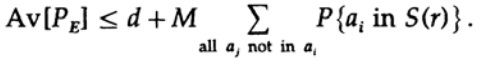
Para cualquier mensaje en particular, al promediar todos los libros de códigos, la codificación recorre todos los valores posibles, por lo que la probabilidad promedio de que un punto esté en una esfera es la relación del volumen de la esfera con el volumen total del espacio. El alcance de la esfera.



donde s = Q + e2 <1/2 y ns debe ser un número entero.

El último término a la derecha es el más grande en esta suma. Primero, estimamos su valor mediante la fórmula de Stirling para factoriales. Luego observamos el coeficiente de reducción del término frente a él, tenga en cuenta que este coeficiente aumenta cuando se mueve hacia la izquierda y, por lo tanto, podemos: (1) limitar el valor de la suma a la suma de la progresión geométrica con este coeficiente inicial, (2) expandir la progresión geométrica de ns miembros a número infinito de términos, (3) calcule la suma de la progresión geométrica infinita (álgebra estándar, nada significativo) y finalmente obtenga el valor límite (para un n suficientemente grande):



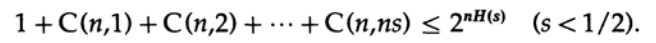
Observe cómo apareció la entropía H (s) en la identidad binomial. Tenga en cuenta que la expansión en la serie de Taylor H (s) = H (Q + e2) proporciona una estimación obtenida teniendo en cuenta solo la primera derivada e ignorando todas las demás. Ahora recojamos la expresión final:



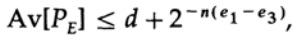
donde



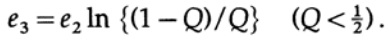
Todo lo que tenemos que hacer es elegir e2 para que e3 <e1, y luego el último término será arbitrariamente pequeño, para n suficientemente grande. Por lo tanto, el error de PE promedio se puede obtener arbitrariamente pequeño con una capacidad de canal arbitrariamente cercana a C.
Si el promedio de todos los códigos tiene un error suficientemente pequeño, entonces al menos un código debe ser adecuado, por lo tanto, existe al menos un sistema de codificación adecuado. Este es un resultado importante obtenido por Shannon: "Teorema de Shannon para un canal con interferencia", aunque debe tenerse en cuenta que lo demostró para un caso mucho más general que para un simple canal simétrico binario que utilicé. Para el caso general, los cálculos matemáticos son mucho más complicados, pero las ideas no son tan diferentes, tan a menudo, usando el ejemplo de un caso especial, uno puede revelar el verdadero significado del teorema.

Critiquemos el resultado. Repetimos repetidamente: "Para n suficientemente grande". ¿Pero qué tan grande es n? Muy, muy grande, si realmente desea estar simultáneamente cerca del ancho de banda del canal y estar seguro de la transferencia de datos correcta. Tan grande que, de hecho, tendrá que esperar mucho tiempo para acumular un mensaje de tantos bits para codificarlo más tarde. Al mismo tiempo, el tamaño del diccionario de código aleatorio será enorme (después de todo, dicho diccionario no puede representarse en una forma más corta que la lista completa de todos los Mn bits, mientras que n y M son muy grandes).

Los códigos de corrección de errores evitan esperar un mensaje muy largo, con su posterior codificación y decodificación a través de libros de códigos muy grandes, porque evitan los libros de códigos per se y utilizan en su lugar cálculos convencionales. En una teoría simple, tales códigos, como regla, pierden su capacidad de acercarse a la capacidad del canal y al mismo tiempo mantienen una tasa de error bastante baja, pero cuando el código corrige una gran cantidad de errores, muestran buenos resultados. En otras palabras, si está colocando algún tipo de capacidad de canal para la corrección de errores, entonces debe usar la opción de corrección de errores la mayor parte del tiempo, es decir, se debe corregir una gran cantidad de errores en cada mensaje enviado, de lo contrario perderá esta capacidad por nada.

¡Además, el teorema demostrado anteriormente todavía no tiene sentido! Muestra que los sistemas de transmisión eficientes deberían utilizar esquemas de codificación sofisticados para cadenas de bits muy largas. Un ejemplo son los satélites que han volado fuera del planeta exterior; A medida que se alejan de la Tierra y del Sol, se ven obligados a corregir cada vez más errores en el bloque de datos: algunos satélites usan paneles solares, que dan alrededor de 5 vatios, otros usan fuentes de energía atómica que dan aproximadamente la misma potencia.La débil potencia de la fuente de alimentación, el pequeño tamaño de las placas transmisoras y el tamaño limitado de las placas receptoras en la Tierra, la gran distancia que debe recorrer la señal; todo esto requiere el uso de códigos con un alto nivel de corrección de errores para construir un sistema de comunicación efectivo.

Regresamos al espacio n-dimensional que usamos en la prueba anterior. Al discutirlo, demostramos que casi todo el volumen de la esfera se concentra cerca de la superficie externa, por lo tanto, casi con certeza la señal enviada se ubicará en la superficie de la esfera construida alrededor de la señal recibida, incluso con un radio relativamente pequeño de dicha esfera. Por lo tanto, no es sorprendente que la señal recibida después de la corrección de un número arbitrariamente grande de errores, nQ, se encuentre arbitrariamente cerca de la señal sin errores. La capacidad del canal de comunicación, que examinamos anteriormente, es la clave para comprender este fenómeno. Tenga en cuenta que las esferas construidas para los códigos de corrección de errores de Hamming no se superponen. Un gran número de mediciones prácticamente ortogonales en el espacio n-dimensional muestran¿Por qué podemos colocar esferas M en un espacio con una ligera superposición? Si permite una superposición pequeña, arbitrariamente pequeña, que puede conducir a un pequeño número de errores durante la decodificación, puede obtener una disposición densa de esferas en el espacio. Hamming garantizó un cierto nivel de corrección de errores, Shannon, una baja probabilidad de error, pero al mismo tiempo mantiene el ancho de banda real arbitrariamente cerca de la capacidad del canal de comunicación, lo que los códigos de Hamming no pueden hacer.pero al mismo tiempo, la preservación del rendimiento real es arbitrariamente cercana a la capacidad del canal de comunicación, lo que los códigos de Hamming no pueden hacer.pero al mismo tiempo, la preservación del rendimiento real es arbitrariamente cercana a la capacidad del canal de comunicación, lo que los códigos de Hamming no pueden hacer.

La teoría de la información no habla sobre cómo diseñar un sistema efectivo, pero indica la dirección del movimiento hacia sistemas de comunicación efectivos. Esta es una herramienta valiosa para construir sistemas de comunicación entre máquinas, pero, como se señaló anteriormente, no tiene mucho que ver con la forma en que las personas intercambian información entre sí. El grado en que la herencia biológica es similar a los sistemas de comunicación técnica es simplemente desconocido, por lo que actualmente no está claro cómo se aplica la teoría de la información a los genes. No tenemos más remedio que intentarlo, y si el éxito nos muestra la naturaleza maquinal de este fenómeno, el fracaso señalará otros aspectos significativos de la naturaleza de la información.

No nos distraigamos mucho. Hemos visto que todas las definiciones iniciales, en mayor o menor medida, deben expresar la esencia de nuestras creencias iniciales, pero se caracterizan por un cierto grado de distorsión y, por lo tanto, no son aplicables. Se acepta tradicionalmente que, en última instancia, la definición que usamos realmente define la esencia; pero, solo nos dice cómo procesar las cosas y de ninguna manera tiene sentido. El enfoque postulativo, tan aclamado en los círculos matemáticos, deja mucho que desear en la práctica.

Ahora veremos un ejemplo de pruebas de coeficiente intelectual, donde la definición es tan cíclica como desee y, como resultado, lo engaña. Se crea una prueba que se supone que mide la inteligencia. Después de eso, se revisa para que sea lo más consistente posible, y luego se publica y calibra de una manera simple para que la "inteligencia" medida se distribuya normalmente (por supuesto, a lo largo de la curva de calibración). Todas las definiciones deben verificarse de manera cruzada, no solo cuando se proponen por primera vez, sino mucho más tarde, cuando se usan en las conclusiones formuladas. ¿En qué medida los límites de definición son adecuados para la tarea en cuestión? ¿Con qué frecuencia las definiciones dadas en las mismas condiciones comienzan a aplicarse en condiciones bastante diferentes? ¡Esto es bastante común!En las humanidades que inevitablemente encontrarás en tu vida, esto sucede con más frecuencia.

Por lo tanto, uno de los objetivos de esta presentación de la teoría de la información, además de demostrar su utilidad, era advertirle sobre este peligro o demostrar cómo usarlo para obtener el resultado deseado. Se ha notado durante mucho tiempo que las definiciones iniciales determinan lo que se encuentra al final, en mucho mayor medida de lo que parece. Las definiciones iniciales requieren que prestes mucha atención no solo en cualquier situación nueva, sino también en áreas con las que has estado trabajando durante mucho tiempo. Esto le permitirá comprender hasta qué punto los resultados obtenidos son una tautología y no algo útil.

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )