Luego, el primero de septiembre, el próximo año académico, sucedieron flores, dulces, lágrimas de felicidad, y eso es todo, y en el proceso de preparación para la conferencia en el instituto me encontré con algunos datos muy interesantes. Vi que esto se podía dibujar rápida y bellamente en GePhi , y me encontré con la historia de Johannes Delitsch. Delich trabajó en Leipzig como maestro de escuela primaria y recopiló datos sobre quién es amigo de quién en su clase en el año escolar 1880. Y esto, en el camino, es uno de los primeros gráficos sociales documentados.

Las clases eran grandes entonces (ya había 53 estudiantes en esta clase en particular), y el viejo Johannes, según tengo entendido, trabajó como tutor hasta 1880. Entonces, al comienzo del nuevo año escolar, después de ver mi extensa cuarta "A" (para ser sincero, no sé cuál era la carta, no es tan importante), Johannes se sintió un poco triste. Aparentemente, él era activo y decidió comprender mejor las relaciones sociales de la mafia que se le había confiado.
Datos
Johannes no era un sociólogo moderno. Era un maestro de escuela, por lo que su metodología de recopilación de datos era bonita, ejem, ecléctica. Habló con los estudiantes, leyó su tarea y "observó cómo se comunican en un grupo". El resultado fue un conjunto de datos bastante frondoso basado en el que Delic escribió un artículo en Zeitschrift für.
Kinderforschung (cualquier palabra en alemán suena y está escrita muy aterradora, lo siento de antemano, pero la traducción literal de "Journal for the Study of Children" suena aún más espeluznante en ruso). Johannes, tal como lo entendí, estaba interesado principalmente en cómo el rendimiento del niño y su popularidad están relacionados entre los compañeros de clase, por lo tanto, además del gráfico direccional que describe con quién es amigo, Delic también le da al estudiante una calificación (desde el más exitoso hasta el más fracasado) y algunos Opciones interesantes. Por ejemplo, había cuatro estudiantes de segundo año en la clase, se destacan en el conjunto de datos. También en la clase había un tipo llamado Lasch, cuya abuela era pastelera. Delic notó que Lash trata a otros niños con dulces y lo notó en sus datos. También identificó por separado a los niños que tenían problemas de salud, como anemia, cojera o retraso en el desarrollo.
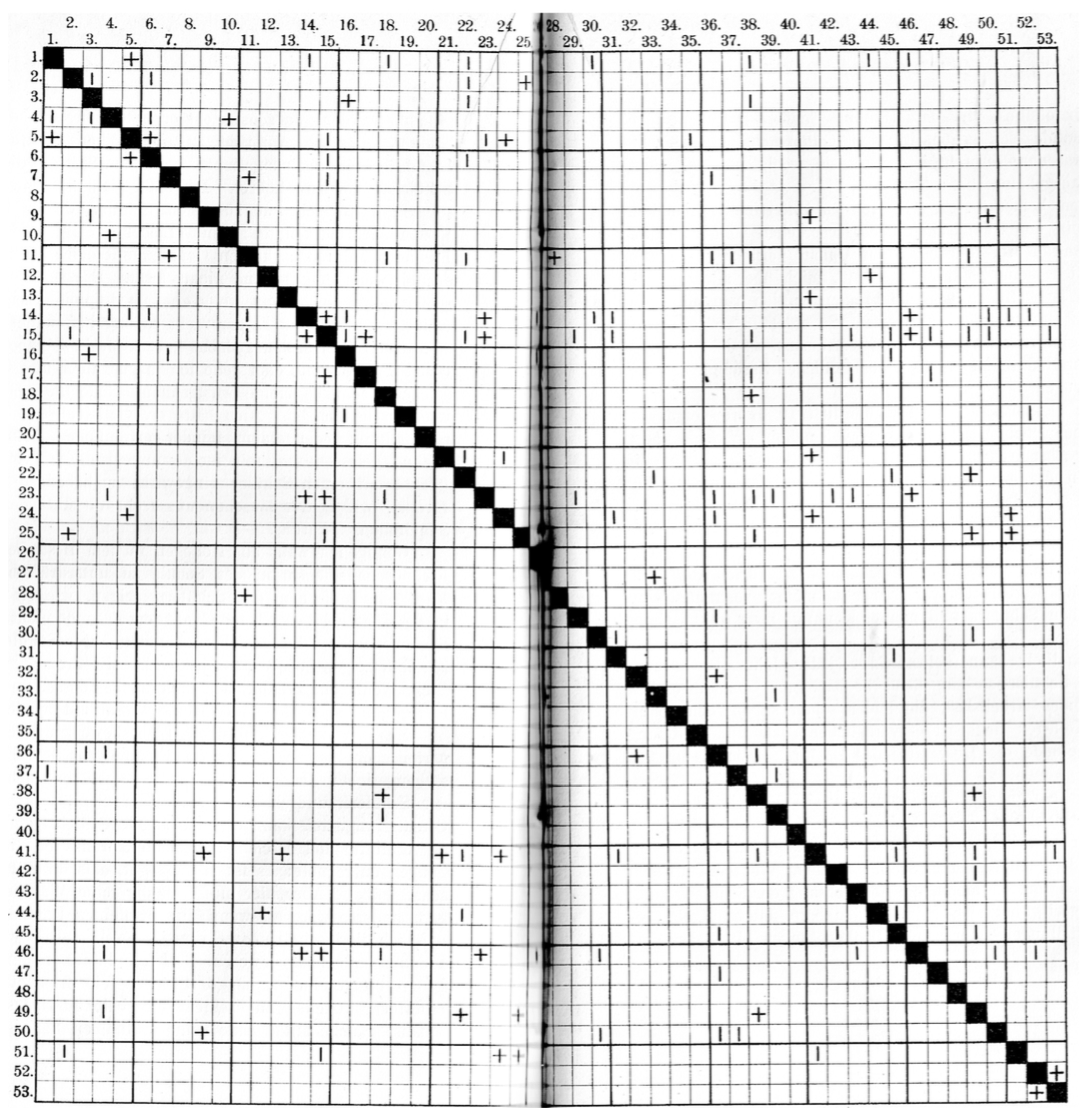
La "Matriz de la amistad" describe quién es amigo y con quién. El conteo está dirigido, porque Hans puede considerar a Frederick como un amigo, y Frederick, tal vez quería estornudar a Hans.
Las mejores personas de nuestra clase.
Pongamos este gráfico social en GePhi, calculemos, por ejemplo, PageRank y coloreemos los vértices.

Los estudiantes más "influyentes" están pintados en un color más saturado.
"Destaquemos" a los siete estudiantes con el PageRank más alto (explicaré por qué exactamente siete más tarde, por ahora, tomemos siete como una constante fundamental). Esto es lo que sucede si selecciona siete vértices del gráfico que tienen el PageRank más alto.

Los líderes de opinión de la cuarta "A" en 1880.
Ya hablamos de estos chicos! En primer lugar, los cuatro niños de segundo año están "en la cima". Decidí destacar a siete personas, porque uno de los niños de cuatro años llamado Schnabel no es muy bueno. Tiene el séptimo valor de PageRank. Mientras que los estudiantes de segundo año Pheil y Vetter con confianza (y con un amplio margen) toman la primera y segunda línea en la lista de "autoridad", y los estudiantes de segundo año Schubert - el cuarto, segundo solo a "autoridad" Lasha (poco puede competir con la distribución de dulces). Schnabel todo séptimo. Mayor autoridad es el mejor estudiante de la clase Schlegel y el quinto estudiante más exitoso en Meinhold. No sabemos nada sobre este Maynhold, Delich no nos dejó ninguna información especial sobre él, por lo tanto, lo designaremos como un "tipo extraño" en la imagen.
Ritmos de pandereta y cálculo de clase de modularidad
GePhi tiene una herramienta para encontrar grupos de interés en nuestro cuarto grupo "A". El algoritmo se describe aquí , y la implementación utilizada por GePhi está aquí . La idea general es que el algoritmo intenta evaluar qué comunidades dentro de la red son más densas. En unos pocos pasos, el algoritmo puede dar un desglose diferente en las comunidades, por lo que todo lo que viene a continuación es tirar y soplar una pandereta en función de un solo resultado, lo que no hace que el proceso sea menos divertido. Entonces, nuestro cuarto algoritmo de búsqueda de la comunidad "A" pintó esos colores.

Dime con quién eres amigo y te diré que eres en vano.
Veamos que pasó. Todos nuestros siete tipos más influyentes cayeron en cuatro comunidades principales. Tres rondas "geniales" de año, Pfail, Fetter y Schubert cayeron en la comunidad, pintadas de verde en la imagen. El repetitivo "Nekrutoy" Schnabel y el mejor alumno de la clase Schlegel cayeron en una comunidad pintada de púrpura. Finalmente, Lash, el distribuidor de dulces, cayó en la comunidad indicada en la imagen en azul claro. Meinhold sigue siendo un hombre misterioso. Terminó en un pequeño grupo de "favoritos", en el que solo hay tres estudiantes (incluido él mismo), ella está pintada en gris oscuro. De los cuatro niños que tenían problemas de salud, dos no eran amigos de nadie y los otros dos cayeron en la comunidad azul.
Pues bien. Mucho está empezando a aclararse. Schnabel, al parecer, no es una repetición tan "genial", porque en lugar de pasar el rato con tipos duros, se comunica con algunos nerds que son amigos del chico compartido Schlegel (es interesante que Schnabel y Schlegel no sean amigos, pero caen de manera estable en una comunidad al calcular la modularidad de la red). Lash y sus dulces formaron una comunidad de tipos que no son ni nerds ni malos, y Meinhold ... Hmmm ... ¿Quién es Meinhold? Veamos quién más está con él "en una fiesta". Dos estudiantes más que cayeron en la misma comunidad con él son Mayer (Meier, cuarto en la calificación de estudiantes) y Flash (Flasch, trigésimo quinto en la calificación de estudiantes). Hmmm ... Tres tipos que ya no se comunican realmente con nadie, pero dos de ellos están aprendiendo bastante bien ...

Fotograma de la película Superbad.
En resumen, me gusta pensar en estos tres tipos como una trinidad de geeks de la Alemania del siglo XIX. Dos de ellos estudian bien, y el tercero no se comunica con nadie especialmente, simplemente hace un robot humanoide gigante o kriegsmarine después de la escuela, o algo peor. No es el punto.
Vamos a traducir la calificación de los escolares alemanes a una calificación promedio. Generaremos algo similar a la distribución normal en el rango de 2 a 5 (los alemanes tienen una escala de calificación inversa, pero a nuestro entender haremos todo de acuerdo con nuestra escala habitual, cuando 2 no pasó y 5 es atractivo). Asociamos a cada estudiante con su puntaje promedio para que cuando se clasifique por este puntaje promedio, se obtenga la misma calificación que en los datos de Delich. Ahora veamos cuál es el puntaje promedio para los estudiantes en cada uno de estos cuatro grupos. Y al mismo tiempo, cuántas personas son en promedio un miembro de cada grupo, y cuántas personas son en promedio amigables con él. El resultado es este:
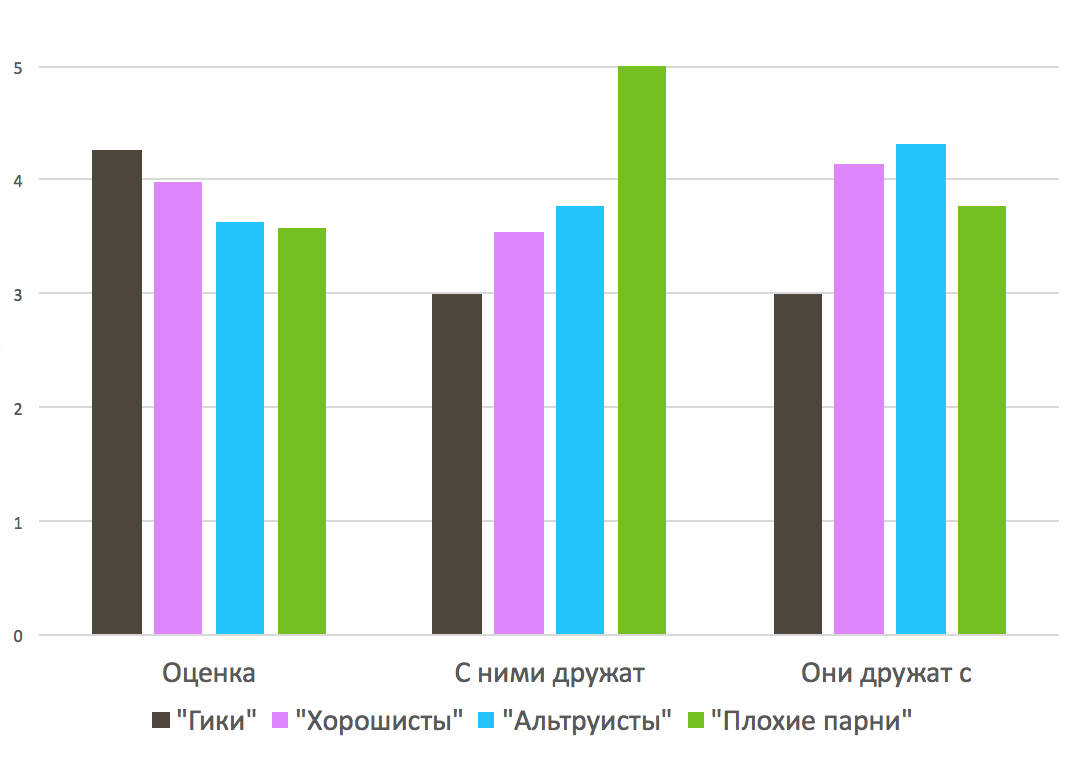
El puntaje promedio y el promedio de entrada y salida de cuatro grupos. Los colores corresponden al color del gráfico.
Los geeks, en general, estudian bien, pero ellos mismos no están ansiosos por hacer amigos, y nadie será amigo de ellos tampoco. Los buenos académicos del grupo de Schlegel y Schnabel estudian en promedio peor que los geeks, pero en términos sociales les está yendo mejor. Los altruistas (como llamé al grupo en el que Lash estaba distribuyendo dulces) estudian mal pero son amigos de otros niños de manera más activa (aunque no mutuamente). Finalmente, los malos aprenden lo peor, pero son muy populares (quieren ser amigos de ellos), aunque ellos mismos no están lejos de ser geeks en términos de la cantidad de personas con las que son amigos.
Dibujemos con quienes los representantes de diferentes comunidades son amigos
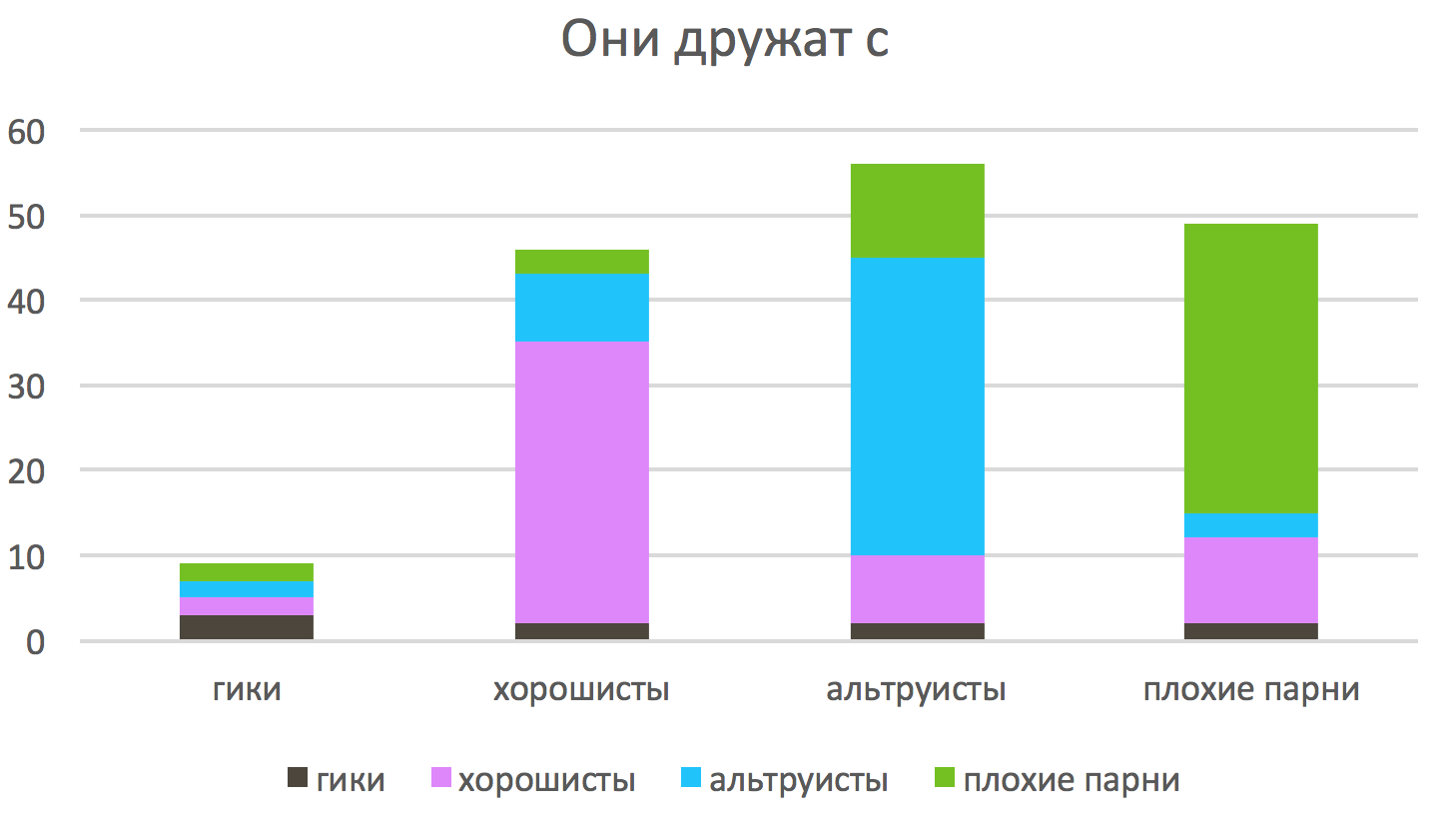
Cada comunidad es la mayoría de los amigos en sí misma, pero interactúa con otras comunidades de diferentes maneras.
¡Mira qué gracioso! Los altruistas consideran a sus amigos muchos buenos y muchos malos. Los malos de los altruistas no son particularmente favorables, pero aquí consideran que algunos buenos son sus amigos. Las personas buenas, a juzgar por todo, no están contentas con la amistad con los malos, pero los altruistas con sus rostros sonrientes y dulces gratis despiertan su moderado interés.
Si por alguna razón estás más interesado en mirar desde otro lado, aquí hay otra foto de premio.

Cada comunidad es la mayoría de los amigos en sí misma, pero interactúa con otras comunidades de diferentes maneras.
Aquí hay un conjunto de datos tan divertido en la primera semana de otoño. En 2014, los datos de nuestra cuarta "A" fueron redescubiertos por este artículo . El hecho es que después de la Primera Guerra Mundial, Alemania no estaba a la altura de la pedagogía, por lo que los datos recopilados por Delic se olvidaron durante mucho tiempo, pero ahora resulta que este es casi el primer gráfico social completamente documentado. Tales cosas
Los datos originales fueron publicados en el artículo:
Delitsch, J., 1900. Über Schülerfreundschaften in einer Volksschule. Zeitschrift für Kinderforschung 5, 150–162.
PD: Me preguntaron varias veces qué tipo de moralidad es esta. Creo que la moraleja aquí es.
En primer lugar, incluso unas pocas columnas de números pueden ocultar el drama. Sí, incluso qué.
En segundo lugar, para cualquier persona que trabaje con datos, la respuesta a la pregunta "¿cuál es la moraleja?" se reduce a la pregunta "¿cuál es la métrica de calidad?"
Si la métrica es el rendimiento académico, entonces es mejor ser amigo de excelentes estudiantes. Todos los estudiantes de segundo año, de hecho, no están en la parte superior de la calificación de la clase, pero no están en la parte inferior en términos de rendimiento académico. Pasan el rato en algún lugar en el medio, pero otros niños en su comunidad aprenden mucho peor. Quizás el rendimiento relativamente bueno de los estudiantes de segundo año se deba al hecho de que la escuela alemana del siglo XIX prestó mucha atención al entrenamiento físico y al deporte, por lo que en parte el "rendimiento" de los estudiantes de segundo año es exagerado debido al hecho de que son físicamente más fuertes. La comunidad alrededor de Schlegel y la comunidad de geeks, a pesar de este sesgo, estudian mucho mejor que la comunidad que se formó alrededor de los estudiantes de segundo año.
Si la métrica es popular entre sus pares, entonces dispersar dulces es una forma bastante costosa y no muy efectiva de ganar esta misma popularidad. Por un lado, funciona: Lash es el tercer estudiante más popular de la clase. Por otro lado, la "calidad" de su comunidad (por la métrica de popularidad social) es bastante baja. Es decir, los dulces te permiten ser popular entre personas no muy populares. Otros chicos populares con Lasha no son amigos (ni repetidores, ni el mejor alumno de la clase Schlegel).
Finalmente, si la métrica es el número de amigos "verdaderos" (donde un verdadero amigo no es una persona con la que eres amigo, sino solo aquellos de tus amigos que son amigos contigo), entonces ser un estudiante de segundo año es solo eso.