Esconderse sin esconderse. Una vez más sobre la esteganografía LSB, chi-cuadrado y ... ¿singularidad?

Hoy, volveremos a subir el viejo nido y hablaremos sobre cómo ocultar un montón de bits en la imagen con un gato, veremos varias herramientas disponibles y analizaremos los ataques más populares. Y parece, ¿qué tiene que ver la singularidad con él?

Como dicen, si quieres descubrir algo, ¡escribe un artículo sobre eso en Habr! (Precaución, mucho texto e imágenes)



La esteganografía (literalmente de la "criptografía" griega) es la ciencia de transmitir datos ocultos (mensajes de stego) en otros datos abiertos (stegocontenedores) mientras se oculta el hecho mismo de la transferencia de datos. No se alarme, de hecho, no todo es tan complicado.

Entonces, ¿en qué parte de la imagen puedes ocultar el mensaje para que nadie lo note?

Y solo hay dos lugares: los metadatos y la imagen misma. Este último es bastante simple, simplemente escriba "exif" en Google. Entonces, comencemos de inmediato con el segundo.

Poco significativo

El modelo de color más popular es RGB, donde el color se representa en forma de tres componentes: rojo, verde y azul . Cada componente está codificado en la versión clásica con 8 bits, es decir, puede tomar un valor de 0
a 255. Es aquí donde se esconde el bit menos significativo. Es importante comprender que uno de esos colores RGB representa tres de esos bits.

Para presentarlos más claramente, haremos un par de pequeñas manipulaciones.

Según lo prometido, tome una foto de un gato en formato png.



Lo dividimos en tres canales y en cada canal tomamos el bit menos significativo. Cree tres nuevas imágenes, donde cada píxel representa NZB. Cero: el píxel es blanco, la unidad es respectivamente negra.

Nosotros entendemos esto.




Pero, como regla, la imagen se encuentra en la "forma ensamblada". Para representar el NZB de los tres componentes en una imagen, es suficiente reemplazar el componente en un píxel donde el NZB es la unidad, reemplazarlo con 255 y, de lo contrario, reemplazarlo con 0.

Pero no menos significativo

Imagine que todo lo que vimos en la última foto es nuestro y que tenemos derecho a hacer cualquier cosa con él. Luego lo tomamos como una secuencia de bits, desde donde podemos leer y donde podemos escribir.

Tomamos los datos que queremos intercalar en la imagen, los presentamos en forma de bits y los escribimos en lugar de los existentes.

Para extraer estos datos, leemos el NZB como un flujo de bits y lo llevamos a la forma deseada. Para saber cuántos bits deben contarse, por regla general, el tamaño del mensaje se escribe al principio. Pero estos son detalles de implementación.

Cabe señalar que en aproximadamente el 50% de los casos, el bit que queremos escribir y el bit de la imagen coincidirán y no tendremos que cambiar nada.

Eso es todo, el método termina aquí.

Por que funciona

Echa un vistazo a las imágenes a continuación.

Este es un contenedor vacío:



Y esto está lleno al 95%:



¿Ves la diferencia? Pero ella es. Por qué

Veamos dos colores: (0, 0, 0) y (1, 1, 1), es decir, colores diferentes solo por el NZB en cada componente.



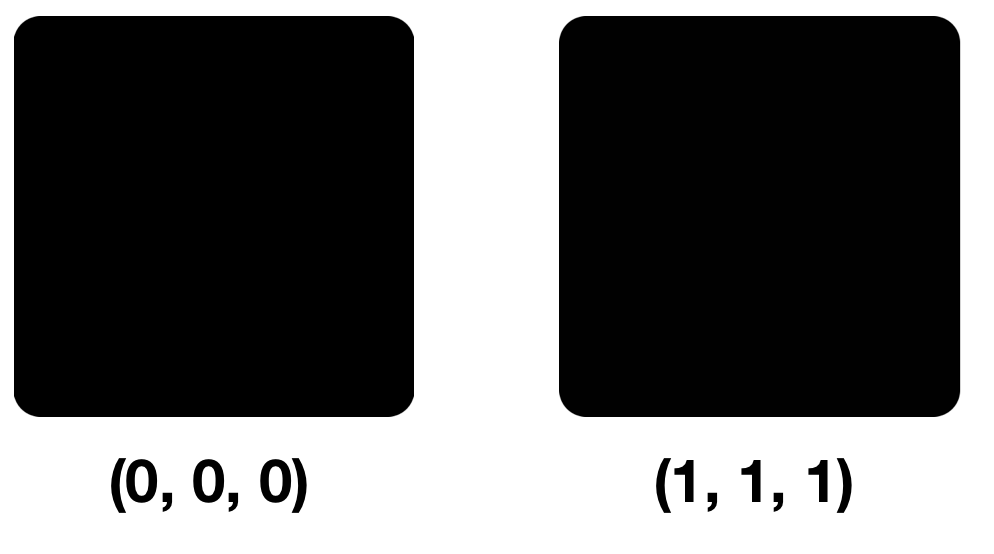
No se notarán pequeñas diferencias en los píxeles a primera, segunda y tercera mirada. El hecho es que nuestro ojo puede distinguir unos 10 millones de colores, y el cerebro tiene solo unos 150. El modelo RGB también contiene 16.777.216 colores. Puedes intentar distinguirlos a todos aquí.

Desde la línea de comando

No hay muchas herramientas de línea de comandos de código abierto disponibles que representen la esteganografía LSB.

El más popular se puede encontrar en la tabla a continuación.

Donde esta el gato

Y el primero en la lista de ataques contra la esteganografía LSB es un ataque visual. Suena raro, ¿no? Después de todo, el gato con un secreto no se traicionó a sí mismo como un contenedor lleno de stego a primera vista. Hmmm ... Solo necesitas saber dónde mirar. Es fácil adivinar que solo el NZB merece nuestra atención.

Para un stegocontainer lleno, la imagen con NZB se ve así:



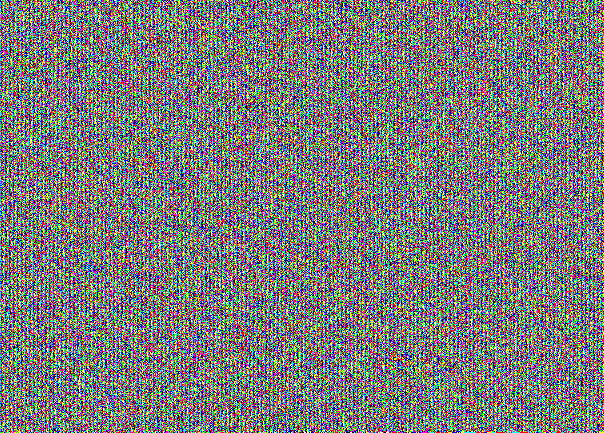
No lo creo? Aquí tienes NZB de los tres canales por separado:




Este es un "dibujo" específico para ocultar el mensaje en el NZB. A primera vista, esto parece un simple ruido. Pero al considerar la estructura es visible. Aquí puedes ver que el stegocontainer está lleno. Si tomáramos un mensaje al 30% de la capacidad de un gato pobre, obtendríamos esta imagen:


Su NZB:



~ 70% del gato permanece sin cambios.

Aquí vale la pena hacer una pequeña digresión y hablar de tamaños. ¿Qué es un gato al 30%? El tamaño del gato es de 603x433 píxeles. El 30% de este tamaño es 78459 píxeles. Cada píxel contiene 3 bits de información. Total 78459 3 = 235377 bits o un poco menos de 30 kilobytes cabe en el 30% del sello. Y en todo el gato cabrá unos 100 kilobytes. Tales cosas

Pero estamos aquí para ti por una razón. ¿Cómo, entonces, engañar a los ojos?
Primer pensamiento: pegue el mensaje en el ruido. Pero no estaba allí. El siguiente es un fragmento del stegocontainer lleno y su LSB.



Con un poco de esfuerzo, aún podemos discernir una estructura familiar. ¡No pierdan la esperanza, caballeros!

Ji ji ji

Muchas cosas rompen estadísticas, ya sabes.

Al cambiar algo en la imagen, cambiamos sus propiedades estadísticas. Es suficiente para el analista encontrar una manera de corregir estos cambios.

Andreas Wesfield y Andreas Pfitzmann, de la Universidad de Dresden, iniciaron la buena chi-cuadrado en su trabajo "Ataques a los sistemas esteganográficos", que se puede encontrar aquí.

En lo sucesivo, hablaremos sobre ataques dentro del mismo plano de color, o en el contexto de RGB, sobre ataques en un canal. Los resultados de cada ataque pueden reducirse al promedio y obtener el resultado para la imagen "ensamblada".

Por lo tanto, el ataque Chi-cuadrado se basa en la suposición de que la probabilidad de la aparición simultánea de colores vecinos (diferentes por el bit menos significativo) (par de valores) en un contenedor de estego vacío es extremadamente pequeña. Realmente lo es, puedes creerlo. En otras palabras, el número de píxeles de dos colores adyacentes es significativamente diferente para un contenedor vacío. Todo lo que necesitamos hacer es calcular la cantidad de píxeles de cada color y aplicar un par de fórmulas. De hecho, esta es una tarea simple para probar una hipótesis utilizando la prueba de chi-cuadrado.

¿Un poco de matemática?

Sea h una matriz en el i-ésimo lugar que contiene el número de píxeles del i-ésimo color en la imagen en estudio.

Entonces:

1. Frecuencia de color medida $$$i = 2k$ :
   

   $$

   $$n_k = h [2k], ~ k \ en [0, 127];$$
   
   
2. Frecuencia de color teóricamente esperada $$$i = 2k$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ in [0,127];$$
   
   

Traducir esto a Python producirá algo como esto:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

Donde histograma es el número de píxeles de color i en la imagen, $$$i \ en [0, 255]$

El criterio de chi-cuadrado para el número de grados de libertad k-1 se calcula de la siguiente manera (k es el número de colores diferentes, es decir, 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

Y finalmente, P es la probabilidad de que las distribuciones $$$n_i$ y $$$n_i ^ *$ En estas condiciones son iguales (la probabilidad de que tengamos un contenedor lleno). Se calcula integrando la función de suavidad:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

Es más efectivo aplicar un chi-cuadrado no a toda la imagen, sino solo a sus partes, por ejemplo, a las líneas. Si la probabilidad calculada para la línea es mayor que 0.5, complete la línea en la imagen original con rojo. Si menos, entonces verde. Para un gato con 30% de plenitud, la imagen se verá de la siguiente manera:



Muy bien, ¿no es así?

Bueno, tenemos un ataque matemáticamente sólido, ¡no puedes engañar a las matemáticas! O ... ??

Baile aleatorio

La idea es bastante simple: escribir bits no en orden, sino en lugares aleatorios. Para hacer esto, debe tomar el PRSP, configurarlo para emitir la misma secuencia aleatoria con el mismo lado (también conocido como contraseña). Sin conocer la contraseña, no podremos configurar el PRNG y encontrar los píxeles en los que se oculta el mensaje. Lo probaremos en un gato.

Gatito (32% de finalización):



Su LSB:



La imagen parece ruidosa, pero no sospechosa para un analista inexperto. ¿Qué dice Chi-cuadrado?


Parece que el sombrero negro ganó! No importa cómo ...

Regularidad-Singularidad

Otro método estadístico fue Jessica Friedrich, Miroslav Golyan y Andreas Pfitzman en 2001. Fue nombrado como el método RS. El artículo original se puede tomar aquí.

El método contiene varios pasos preparatorios.

La imagen se divide en grupos de n píxeles. Por ejemplo, 4 píxeles consecutivos en una fila. Como regla general, dichos grupos contienen píxeles adyacentes.
Para nuestro gato con relleno secuencial en el canal rojo, los primeros cinco grupos serán:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(Todas las medidas están en la versión clásica de RGB)

Luego definimos la llamada función discriminante o función de suavidad, que asigna cada grupo de píxeles a un número real. El propósito de esta función es capturar la suavidad o "regularidad" del grupo de píxeles G. Cuanto más ruidoso sea el grupo de píxeles $$$G = (x_1, ..., x_n)$ , más importante será la función discriminante. Muy a menudo, se elige una "variación" de un grupo de píxeles o, más simplemente, la suma de las diferencias de píxeles vecinos en un grupo. Pero también puede tener en cuenta los supuestos estadísticos sobre la imagen.

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

Los valores de la función de suavidad para un grupo de píxeles de nuestro ejemplo:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

A continuación, se determina la clase de funciones de volteo de un píxel.

Deben tener algunas propiedades.

$$

$$1. ~~~ \ forall x \ en P: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255;$$

$$

$$3 ~~~ \ forall x \ en P: ~ F _ {- 1} (x) = F_1 (x + 1) -1;$$

Donde $$$F$ - cualquier función de una clase, $$$F_1$ Es una función de volteo directo, y $$$F _ {- 1}$ - reversa. Además, la función de volteo idéntica generalmente se denota $$$F_0$ que no cambia el píxel.

Las funciones de volteo de Python podrían verse así:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

Para cada grupo de píxeles, aplicamos una de las funciones de inversión y, en función del valor de la función discriminante antes y después de la inversión, determinamos el tipo de grupo de píxeles: normal ( R egular), único / inusual ( S ingular) e inutilizable. Dado que el último tipo no se usa más, el método recibió el nombre de las primeras letras de los tipos de clave. Ese es todo el secreto del nombre, la singularidad no tiene nada que ver con eso :)



Es posible que queramos aplicar diferentes volteos a diferentes píxeles, para esto definimos una máscara M con n valores de -1, 0 o 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n))$$

Deje que la máscara para nuestro ejemplo sea clásica: [1, 0, 0, 1]. Se descubrió experimentalmente que las máscaras simétricas que no contienen $$$F _ {- 1}$ . También las opciones exitosas serían: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Aplicamos volteo para los grupos del ejemplo, calculamos el valor de suavidad y determinamos el tipo de grupo de píxeles:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  Grupo inutilizable
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  Grupo regular
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) Grupo singular
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) Grupo singular
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  f (77, 76, 76, 76) = 1 = 1 = f (76, 76, 76, 77)
  Grupo inutilizable
  
  

Denotamos el número de grupos regulares para la máscara M como $$$R_M$ (en porcentajes de todos los grupos), y $$$S_M$ para grupos singulares.

Entonces $$$R_M + S_M \ leq 1$ y $$$R _ {- M} + S _ {- M} \ leq 1$ , para una máscara negativa (todos los componentes de la máscara se multiplican por -1), porque $$$R_M + S_M + U_M = 1$ mientras que $$$U_M$ Puede estar vacío. Del mismo modo para una máscara negativa.

La hipótesis estadística principal es que en una imagen típica el valor esperado $$$R_M$ igual a $$$R _ {- M}$ , y lo mismo es cierto para $$$S_M$ y $$$S _ {- M}$ . Esto se demuestra mediante datos experimentales y algunos bailes con una pandereta alrededor de la última propiedad de la función de volteo.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

Vamos a verlo en nuestro pequeño ejemplo? Dado el pequeño tamaño de la muestra, es posible que no confirmemos esta hipótesis. Veamos qué sucede con la máscara invertida: [-1, 0, 0, -1].

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  Grupo regular
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  Grupo regular
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  Grupo regular
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  Grupo regular
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  Grupo regular
  
  

Bueno, todo es obvio.

Sin embargo, la diferencia entre $$$R_M$ y $$$S_M$ tienden a cero a medida que aumenta la longitud m del mensaje incrustado y obtenemos que $$$R_M \ cong S_M$ .

Es curioso que la aleatorización del plano LSB tenga el efecto contrario en $$$R _ {- M}$ y $$$S _ {- M}$ . Su diferencia aumenta con la longitud m del mensaje incrustado. Una explicación de este fenómeno se puede encontrar en el artículo original.

Aquí esta el horario $$$R_M$ , $$$S_M$ , $$$R _ {- M}$ y $$$S _ {- M}$ dependiendo del número de píxeles con LSB invertidos, se llama diagrama RS. El eje x es el porcentaje de píxeles con LSB invertidos, el eje y es el número relativo de grupos regulares y singulares con máscaras M y -M, $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



La esencia del método de esteganálisis RS es evaluar las cuatro curvas del diagrama RS y calcular su intersección mediante extrapolación. Supongamos que tenemos un stegocontainer con un mensaje de longitud desconocida p (como porcentaje de píxeles) incrustado en los bits más bajos de píxeles seleccionados al azar (es decir, usando RandomLSB). Nuestras mediciones iniciales del número de grupos R y S corresponden a puntos $$$R_M (p / 2)$ , $$$S_M (p / 2)$ , $$$R _ {- M} (p / 2)$ y $$$S _ {- M} (p / 2)$ . Tomamos puntos de exactamente la mitad de la longitud del mensaje, ya que el mensaje es un flujo de bits aleatorio y, en promedio, como se mencionó anteriormente, solo la mitad de los píxeles se cambiarán al incrustar el mensaje.

Si invertimos el LSB de todos los píxeles en la imagen y calculamos el número de grupos R y S, obtenemos cuatro puntos $$$R_M (1-p / 2)$ , $$$S_M (1-p / 2)$ , $$$R _ {- M} (1-p / 2)$ y $$$S _ {- M} (1-p / 2)$ . Dado que estos dos puntos dependen de la aleatorización específica del LSB, debemos repetir este proceso muchas veces y evaluar $$$R_M (1/2)$ y $$$S_M (1/2)$ de muestras estadísticas

Podemos dibujar líneas condicionalmente a través de puntos $$$R _ {- M} (p / 2)$ , $$$R _ {- M} (1-p / 2)$ y $$$S _ {- M} (p / 2)$ , $$$S _ {- M} (1-p / 2)$ .

Puntos $$$R_M (p / 2)$ , $$$R_M (1/2)$ , $$$R_M (1-p / 2)$ y $$$S_M (p / 2)$ , $$$S_M (1/2)$ , $$$S_M (1-p / 2)$ definir dos parábolas Cada parábola y la línea correspondiente se cruzan a la izquierda. La media aritmética de las coordenadas x de ambas intersecciones nos permite estimar la longitud desconocida del mensaje p.

Para evitar una estimación estadística larga de los puntos medios RM (1/2) y SM (1/2), se pueden tomar un par de consideraciones más:

1. Punto de intersección de curvas $$$R_M$ y $$$R _ {- M}$ tiene la misma coordenada x que el punto de intersección para las curvas $$$S_M$ y $$$S _ {- M}$ . Esta es esencialmente una versión más rigurosa de nuestra hipótesis estadística. (ver arriba)
2. Las curvas RM y SM se cruzan en m = 50%, o $$$R_M (1/2) = S_M (1/2)$ .

Estos dos supuestos proporcionan una fórmula simple para la longitud del mensaje secreto p. Después de escalar el eje x para que p / 2 se convierta en 0 y 1 - p / 2 se convierta en 1, la coordenada x del punto de intersección es la raíz de la siguiente ecuación cuadrática



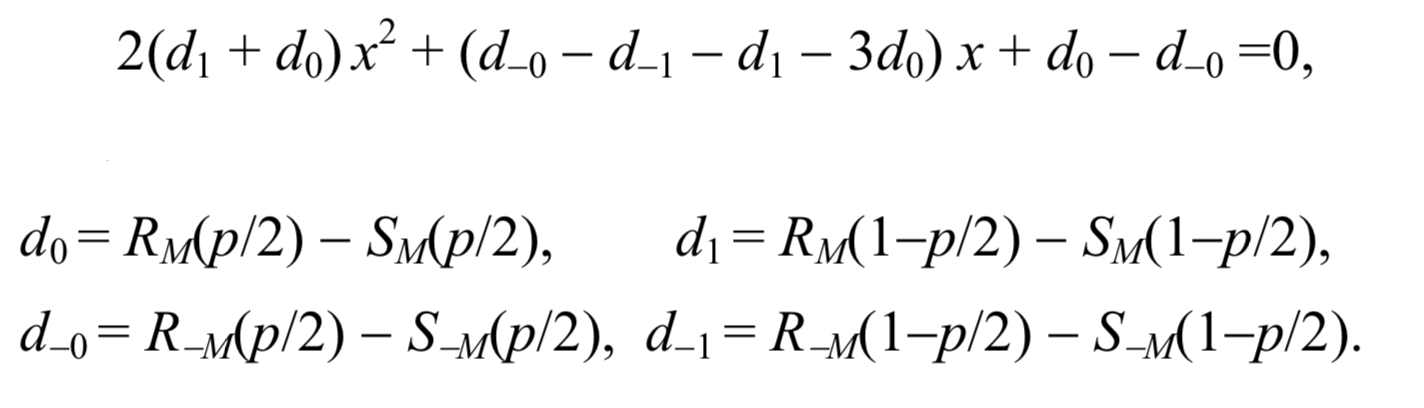
Entonces la longitud del mensaje puede calcularse mediante la fórmula:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

Aquí nuestro gato entra en escena. (¿No es hora de darle un nombre?)

Entonces tenemos:

• Grupos RM regulares (p / 2): 23121 pcs.
• Grupos SM singulares (p / 2): 14124 pcs.
• Grupos regulares con máscara invertida RM (p / 2): 37191 pcs.
• Grupos singulares con máscara invertida SM (p / 2): 8440 piezas.
• Grupos regulares con LSB RM invertido (1-p / 2): 20298 pcs.
• Grupos singulares con LSB SM invertido (1-p / 2): 16206 pcs.
• Grupos regulares con LSB invertido y con máscara invertida RM (1-p / 2): 40603 pcs.
• Grupos singulares con LSB invertido y con máscara invertida SM (1-p / 2): 6947 piezas.

(Si tienes mucho tiempo libre, puedes calcularlos tú mismo, pero por ahora te sugiero que creas mis cálculos)

En la agenda, hemos dejado una matemática desnuda. ¿Todavía recuerdas cómo resolver ecuaciones cuadráticas?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

Sustituyendo todo d en la fórmula anterior, obtenemos una ecuación cuadrática, que resolvemos como se enseña en la escuela.

$$

$$26178x ^ 2-35988x - 19754 = 0$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0.4204$$

Tome una raíz de módulo más pequeña , es decir $$$x_2$ . Entonces la estimación aproximada para el mensaje integrado en el gato será la siguiente:

$$

$$p = \ frac {-0.4204} {- 0.4204 - 0.5} = 0.4567$$

Sí, este método tiene una gran ventaja y una gran desventaja. La ventaja es que el método funciona tanto con la esteganografía LSB ordinaria como con la esteganografía RandomLSB. Un chi-cuadrado no puede presumir de tal oportunidad. El método reconoció a nuestro gato de aspecto aleatorio con precisión y estimó la longitud del mensaje en 0.3256, que es muy, muy precisa.

El menos radica en el error grande (muy grande) de este método, que crece junto con el mensaje largo con incrustación secuencial . Por ejemplo, para un gato con una ocupación del 30%, mi implementación del método proporciona una estimación promedio aproximada para tres canales de 0.4633 o 46% de la capacidad total, con una ocupación de más del 95% - 0.8597. Pero para un gato vacío hasta 0.0054. Y esta es una tendencia general que es independiente de la implementación. Los resultados más precisos con el método LSB ordinario dan una longitud de mensaje integrada de 10% + - 5%.

Más o menos

Para no quedar atrapado, uno debe ser inesperado y usar una codificación de ± 1. En lugar de cambiar el bit menos significativo en el byte de color, aumentaremos o disminuiremos el byte completo en uno. Solo hay dos excepciones:

• no podemos reducir cero, por lo tanto lo incrementaremos,
  
• tampoco podemos aumentar 255, por lo que siempre disminuiremos este valor.
  

Para todos los demás valores de bytes, seleccionamos completamente al azar un aumento de uno o una disminución. Además de esta manipulación, el LSB cambiará como lo hizo antes. Para una mayor confiabilidad, es mejor tomar bytes aleatorios para grabar un mensaje.

Aquí está nuestro gato amigo:



Exteriormente, la introducción es imperceptiblemente exacta por la misma razón por la cual las diferencias entre (0, 0, 0) y (1, 1, 1) no eran visibles.



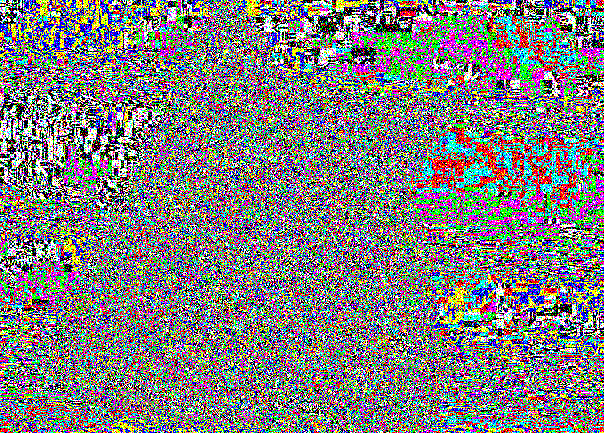
El segmento LSB sigue siendo simplemente ruidoso debido a la grabación en lugares aleatorios.



El chi-cuadrado aún es ciego, y el método RS da una estimación aproximada de 0.0036 .

Para no ser muy feliz, lea este artículo aquí.

Los más atentos pueden preguntar cómo podemos obtener un mensaje si los bytes completos se cambian aleatoriamente, y no tenemos una contraseña para configurar el PRNG (es mejor usar diferentes semillas, también conocido como el estado del generador, también contraseñas para trabajar con RandomLSB y codificación ± 1). La respuesta es lo más simple posible. Recibimos el mensaje de la misma manera que lo hicimos sin codificación ± 1. Es posible que ni siquiera sepamos sobre su uso. Repito, usamos este truco solo para evitar las herramientas de detección automática . Al incrustar / recuperar un mensaje, trabajamos solo con su LSB y nada más. Sin embargo, al detectar, debemos tener en cuenta el contexto de implementación, es decir, todos los bytes de la imagen, para generar estimaciones estadísticas. Este es precisamente todo el éxito de la codificación ± 1.

En lugar de una conclusión

Otro muy buen intento de usar estadísticas contra la esteganografía LSB se realizó en un método llamado Sample Pairs. Lo puedes encontrar aquí. Su presencia aquí haría que el artículo fuera demasiado académico, así que lo dejo interesado para la lectura extracurricular. Pero anticipándome a las preguntas de la audiencia, responderé de inmediato: no, él no capta ± 1 codificación.

Y, por supuesto, el aprendizaje automático. Los métodos modernos basados ​​en ML dan muy buenos resultados. Puedes leer sobre esto aquí y aquí .

Basado en este artículo, se escribió una pequeña herramienta (por ahora). Puede generar datos, realizar un ataque visual por separado en los canales, calcular la evaluación RS-, SPA y visualizar los resultados del Chi-cuadrado. Y ella no va a parar allí.

Para resumir, quiero dar un par de consejos:

• Incruste el mensaje en bytes aleatorios.
• Reduzca la cantidad de información incrustada tanto como sea posible (recuerde tío Hamming).
• Use ± 1 codificación.
• Elija imágenes con ruido de LSB.
• UPD de Remdalp : usa imágenes que no aparecen en ningún lado.
• Se amable!

¡Me alegrará ver sus sugerencias, adiciones, correcciones y otros comentarios!

PD: Quiero expresar un agradecimiento especial a PavelMSTU por las consultas y patadas motivacionales.