Una introducción simple a ALU para redes neuronales: explicación, significado físico e implementación

Recientemente, investigadores de Google DeepMind, incluido un reconocido científico de inteligencia artificial, autor del libro " Comprender el aprendizaje profundo " , Andrew Trask, publicó un artículo impresionante que describe un modelo de red neuronal para extrapolar los valores de funciones numéricas simples y complejas con un alto grado de precisión.

En esta publicación explicaré la arquitectura de NALU ( dispositivos de lógica aritmética neural, NALU), sus componentes y las diferencias significativas de las redes neuronales tradicionales. El objetivo principal de este artículo es explicar de manera simple e intuitiva NALU (tanto la implementación como la idea) para científicos, programadores y estudiantes que son nuevos en las redes neuronales y el aprendizaje profundo.

Nota del autor : También recomiendo leer el artículo original para un estudio más detallado del tema.

¿Cuándo están mal las redes neuronales?

Imagen tomada de este artículo.

En teoría, las redes neuronales deberían aproximarse bien a las funciones. Casi siempre pueden identificar correspondencias significativas entre los datos de entrada (factores o características) y la salida (etiquetas u objetivos). Es por eso que las redes neuronales se usan en muchos campos, desde el reconocimiento de objetos y su clasificación hasta la traducción del habla en texto y la implementación de algoritmos de juego que pueden vencer a los campeones mundiales. Ya se han creado muchos modelos diferentes: redes neuronales convolucionales y recurrentes, autocodificadores, etc. El éxito en la creación de nuevos modelos de redes neuronales y aprendizaje profundo es un gran tema en sí mismo.

Sin embargo, según los autores del artículo, ¡las redes neuronales no siempre hacen frente a tareas que parecen obvias para las personas e incluso para las abejas ! Por ejemplo, esta es una cuenta oral u operaciones con números, así como la capacidad de identificar la dependencia de las relaciones. El artículo mostró que los modelos estándar de redes neuronales ni siquiera pueden hacer frente al mapeo idéntico (una función que traduce un argumento en sí mismo, $$$f (x) = x$) Es la relación numérica más obvia. La siguiente figura muestra el MSE de varios modelos de redes neuronales cuando se aprende sobre los valores de esta función.


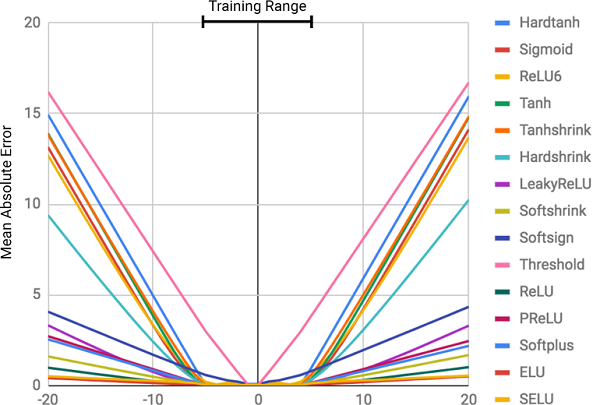La figura muestra el error cuadrado medio para redes neuronales estándar que usan la misma arquitectura y diferentes funciones de activación (no lineales) en las capas internas

¿Por qué están mal las redes neuronales?

Como se puede ver en la figura, la razón principal de los errores es la no linealidad de las funciones de activación en las capas internas de la red neuronal. Este enfoque funciona muy bien para determinar las relaciones no lineales entre los datos de entrada y las respuestas, pero es terriblemente incorrecto ir más allá de los datos en los que la red aprendió. Por lo tanto, las redes neuronales hacen un excelente trabajo al recordar una dependencia numérica de los datos de entrenamiento, pero no pueden extrapolarla.

Esto es como escribir una respuesta o un tema antes de un examen sin comprender el tema. Es fácil aprobar el examen si las preguntas son similares a la tarea, pero si se trata de comprender el tema que se está evaluando y no la capacidad de recordar, fallaremos.


¡Esto no estaba en el programa del curso!

El grado de error está directamente relacionado con el nivel de no linealidad de la función de activación seleccionada. El diagrama anterior muestra claramente que las funciones no lineales con restricciones duras, como una tangente sigmoidea o hiperbólica ( Tanh ), hacen frente a la tarea de generalizar dependencias mucho peor que las funciones con restricciones suaves, como una transformación lineal truncada ( ELU , PReLU ).

Solución: batería neuronal (NAC)

Una batería neural ( NAC ) está en el corazón del modelo NALU . Esta es una parte simple pero efectiva de una red neuronal que hace frente a la suma y la resta , que es necesaria para el cálculo eficiente de las relaciones lineales.

NAC es una capa lineal especial de una red neuronal, en cuyo peso se impone una condición simple: solo pueden tomar 3 valores: 1, 0 o -1 . Dichas restricciones no permiten que la batería cambie el rango de datos de entrada, y permanece constante en todas las capas de la red, independientemente de su número y conexiones. Por lo tanto, la salida es una combinación lineal de los valores del vector de entrada, que puede ser fácilmente una operación de suma y resta.

Reflexiones en voz alta : para una mejor comprensión de esta declaración, veamos un ejemplo de construcción de capas de una red neuronal que realizan operaciones aritméticas lineales en los datos de entrada.


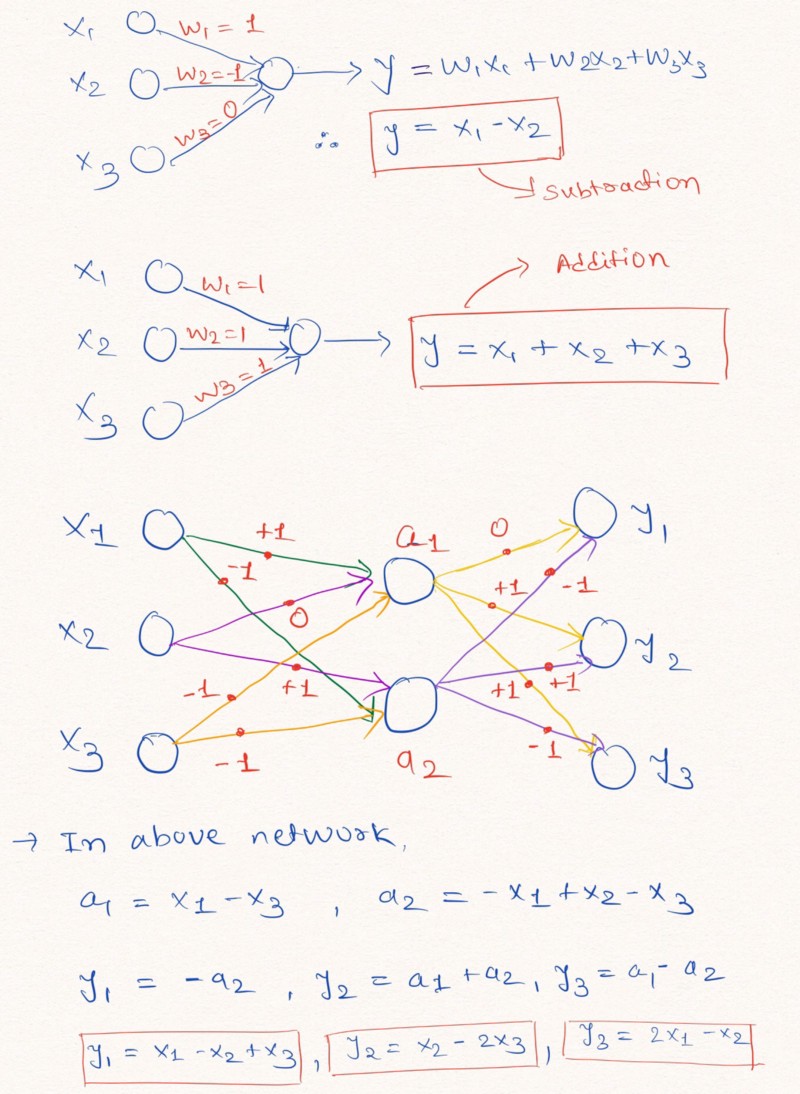La figura ilustra cómo las capas de una red neuronal sin agregar una constante y con posibles valores de pesos -1, 0 o 1, pueden realizar una extrapolación lineal

Como se muestra arriba en la imagen de las capas, la red neuronal puede aprender a extrapolar los valores de funciones aritméticas tan simples como la suma y la resta ( $$$y = x_1 + x_2$y $$$y = x_1 - x_2$), utilizando las restricciones de los pesos con posibles valores de 1, 0 y -1.

Nota: la capa NAC en este caso no contiene un término libre (constante) y no aplica transformaciones no lineales a los datos.

Dado que las redes neuronales estándar no pueden hacer frente a la solución del problema bajo restricciones similares, los autores del artículo ofrecen una fórmula muy útil para calcular dichos parámetros a través de parámetros clásicos (ilimitados) $$$\ hat {W}$y $$$\ hat {M}$. Los datos de peso, como todos los parámetros de las redes neuronales, se pueden inicializar y seleccionar aleatoriamente en el proceso de entrenamiento de la red. Fórmula para calcular vector $$$W$a través de $$$\ hat {W}$y $$$\ hat {M}$se ve así:

$$

$$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$$

La fórmula usa el producto de matriz de elementos

El uso de esta fórmula garantiza el rango limitado de valores W por el intervalo [-1, 1], que está más cerca del conjunto -1, 0, 1. Además, las funciones de esta ecuación son diferenciables por parámetros de peso. Por lo tanto, será más fácil para nuestra capa NAC aprender valores $$$W$utilizando el gradiente de descenso y la propagación hacia atrás del error . El siguiente es un diagrama de la arquitectura de la capa NAC .


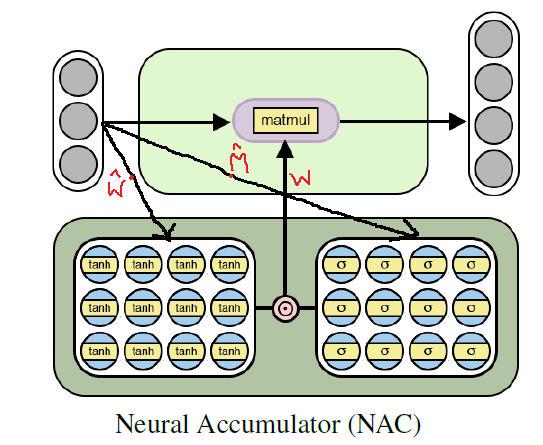La arquitectura de una batería neural para el entrenamiento en funciones aritméticas elementales (lineales)

Implementación de Python NAC usando Tensorflow

Como ya entendimos, NAC es una red neuronal bastante simple (capa de red) con pequeñas características. La siguiente es una implementación de una sola capa NAC en Python usando las bibliotecas Tensoflow y NumPy.


En el código anterior $$$\ hat {W}$y $$$\ hat {M}$se inicializan usando una distribución uniforme, pero puede usar cualquier método recomendado para generar una aproximación inicial para estos parámetros. Puede ver la versión completa del código en mi repositorio de GitHub (el enlace está duplicado al final de la publicación).

Continuando: de la suma y la resta al NAC para expresiones aritméticas complejas

Si bien el modelo de una red neuronal simple descrito anteriormente hace frente a las operaciones más simples, como la suma y la resta, debemos ser capaces de aprender de los muchos significados de funciones más complejas, como la multiplicación, la división y la exponenciación.

A continuación se muestra la arquitectura NAC modificada, que está adaptada para la selección de operaciones aritméticas más complejas a través del logaritmo y tomar el exponente dentro del modelo. Tenga en cuenta las diferencias entre esta implementación de NAC y la ya discutida anteriormente.


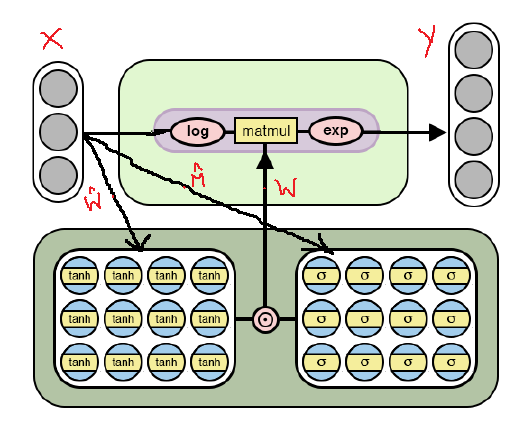Arquitectura NAC para operaciones aritméticas más complejas.

Como se puede ver en la figura, logaritmos los datos de entrada antes de multiplicarlos por la matriz de pesos y luego calculamos el exponente del resultado. La fórmula para los cálculos es la siguiente:

$$

$$Y = exp (W \ bullet (log (| x | + \ epsilon)))$$

La fórmula de salida para la segunda versión de NAC . $$$\ epsilon$Aquí hay un número muy pequeño para evitar situaciones como log (0) durante el entrenamiento

Por lo tanto, para ambos modelos NAC , el principio de funcionamiento, incluido el cálculo de la matriz de peso con restricciones $$$W$a través de $$$\ hat {W}$y $$$\ hat {M}$no cambia La única diferencia es el uso de operaciones logarítmicas en la entrada y salida en el segundo caso.

Segunda versión de NAC en Python usando Tensorflow

El código, como la arquitectura, difícilmente cambiará, excepto por las mejoras indicadas en el cálculo del tensor de los valores de salida.



Le recuerdo nuevamente que la versión completa del código se puede encontrar en mi repositorio de GitHub (el enlace está duplicado al final de la publicación).

Poniendo todo junto: una unidad lógica aritmética neural (NALU)

Como muchos ya han adivinado, podemos aprender de casi cualquier operación aritmética, combinando los dos modelos discutidos anteriormente. Esta es la idea principal de NALU , que incluye una combinación ponderada de NAC elemental y complejo, controlada a través de una señal de entrenamiento. Por lo tanto, los NAC son los componentes básicos para construir NALU , y si comprende su diseño, crear NALU será fácil. Si todavía tiene preguntas, intente leer las explicaciones para ambos modelos NAC nuevamente. A continuación se muestra un diagrama con la arquitectura NALU .


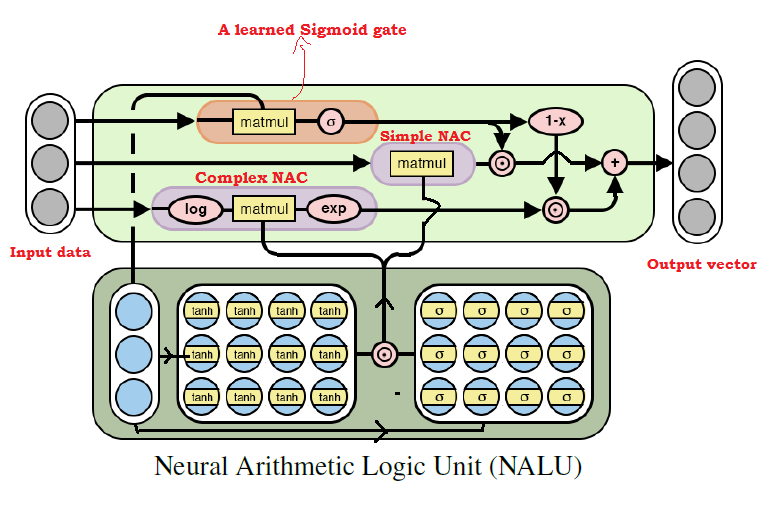Diagrama de arquitectura NALU con explicaciones

Como se puede ver en la figura anterior, ambas unidades NAC (bloques morados) dentro de la NALU se interpolan (combinan) a través de la señal de entrenamiento sigmoide (bloque naranja). Esto le permite (des) activar la salida de cualquiera de ellos, dependiendo de la función aritmética, cuyos valores estamos tratando de encontrar.

Como se mencionó anteriormente, la unidad elemental NAC es una función acumulativa, que permite a la NALU realizar operaciones lineales elementales (suma y resta), mientras que la unidad NAC compleja es responsable de la multiplicación, división y exponenciación. La salida en NALU se puede representar como una fórmula:


De la fórmula NALU anterior, podemos concluir que con $$$g = 0$la red neuronal seleccionará solo valores para operaciones aritméticas complejas, pero no para operaciones elementales; y viceversa, en el caso de $$$g = 1$. Por lo tanto, en general, NALU puede aprender cualquier operación aritmética que consista en sumar, restar, multiplicar, dividir y elevar a una potencia y extrapolar con éxito el resultado más allá de los límites de los intervalos de los valores de los datos de origen.

Implementación de Python NALU usando Tensorflow

En la implementación de NALU, utilizaremos el NAC elemental y complejo, que ya hemos definido.


Una vez más, noto que en el código anterior, nuevamente inicialicé la matriz de parámetros $$$G$usando una distribución uniforme, pero puede usar cualquier forma recomendada para generar una aproximación inicial.

---

Resumen

Para mí personalmente, la idea de NALU es un gran avance en el campo de la IA, especialmente en las redes neuronales, y parece prometedor. Este enfoque puede abrir la puerta a aquellas áreas de aplicación donde las redes neuronales estándar no podrían hacer frente.

Los autores del artículo hablan sobre varios experimentos usando NALU : desde seleccionar valores de funciones aritméticas elementales hasta contar el número de dígitos escritos a mano en una serie dada de imágenes MNIST , lo que permite que las redes neuronales verifiquen programas de computadora.

Los resultados causan una impresión sorprendente y demuestran que NALU hace frente a casi cualquier tarea relacionada con la representación numérica, mejor que los modelos estándar de redes neuronales. Animo a los lectores a familiarizarse con los resultados de los experimentos para comprender mejor cómo y dónde puede ser útil el modelo NALU .

Sin embargo, debe recordarse que ni NAC ni NALU son la solución ideal para cualquier tarea. Más bien, representan la idea general de cómo crear modelos para una clase particular de operaciones aritméticas.

---

A continuación hay un enlace a mi repositorio de GitHub, que contiene la implementación completa del código del artículo.
github.com/faizan2786/nalu_implementation

Puede verificar independientemente el funcionamiento de mi modelo en varias funciones seleccionando hiperparámetros para una red neuronal. Haga preguntas y comparta sus pensamientos en los comentarios de esta publicación, y haré todo lo posible para responderle.

PD (del autor): esta es mi primera publicación escrita, así que si tienes algún consejo, sugerencia y recomendación para el futuro (tanto técnico como general), escríbeme.

PPS (del traductor): si tiene comentarios sobre la traducción o el texto, escríbame un mensaje personal. Estoy especialmente interesado en la redacción de la señal de puerta aprendida: no estoy seguro de poder traducir este término con precisión.