
En este artículo, daré, en mi opinión, una solución interesante al problema del reconocimiento por computadora de objetos en una imagen sin necesidad de capacitación.
Tarea: tener una foto de un edificio de varios pisos, trate de determinar el número de pisos en él.
Una buena estimación del número de pisos puede dar el número de ventanas en la vertical de la casa. Ventanas, balcones y otros objetos son buenas características de los pisos (especialmente en edificios residenciales). Consideraré edificios residenciales, cuyas imágenes son fáciles de encontrar en la red. Una limitación importante se debe notar de antemano: la casa en la imagen debe mostrarse completamente vertical, de modo que sea posible detectar visualmente todos los pisos.
La tarea se divide racionalmente en dos etapas:
- Busque la "franja" vertical de ventanas a contar. Dos subtareas: en primer lugar, debe buscar ventanas en el área de imagen ocupada por la casa, y en segundo lugar, hay muchas ventanas en edificios residenciales, no tiene sentido analizarlas todas. Es necesario resaltar entre ellos la secuencia vertical que mejor se adapta para el análisis posterior.
- Determinación del número de pisos (ventanas u otros objetos característicos) por el área seleccionada de la casa.
Este artículo está dedicado principalmente al primer paso de la solución. El segundo paso aún está en desarrollo, pero también daré algunos resultados de su solución.
Paso 1. Busque el área con ventanas
La idea básica es que una serie de objetos idénticos (como ventanas) que se distinguen bien en una casa en una fila de objetos idénticos crean una secuencia periódica de brillo de píxeles. Esta es precisamente la secuencia que se encuentra. A continuación se muestran las etapas principales del algoritmo.
Primero traducimos la imagen en tonos de gris y la escalamos (utilicé imágenes de 400x600px)

Fig. 1 Imagen original en blanco y negro
Más en el bucle:
- Selección en la imagen de una franja relativamente estrecha (40 px) a toda la altura (Fig. 2, imagen inferior sin puntos)
- Promedio de brillo sobre el ancho de la tira. Resulta la línea w de la distribución del brillo promedio sobre la altura de la casa (Fig. 2 gráfico superior). Tiene una estructura periódica claramente visible característica del área donde hay ventanas. Las ventanas ubicadas en la sombra son menos distinguibles, pero esto no hará daño.
- Se calcula la diferencia dw de los valores de w y w desplazados por la distancia sh. El método de búsqueda utiliza dicho valor de desplazamiento sh para lograr la reducción máxima en la mediana de las diferencias dw (Fig. 2, gráfico inferior).


Fig.2 "Franja" de ventanas
Sin embargo, no es suficiente encontrar la banda de la imagen en la que la mediana se redujo más fuertemente. El hecho es que las áreas con vegetación o cielo, con pequeños valores de cizallamiento, pueden dar una disminución mayor que las ventanas. Pero si graficamos la dependencia del valor medio del valor de desplazamiento para las tiras con y sin ventanas, entonces podemos notar una diferencia clave: para valores de desplazamiento cercanos a la altura de los pisos, el gráfico con ventanas tiene extremos claramente visibles. Por lo tanto, no es necesario medir el nivel absoluto alcanzable de la mediana, sino su disminución máxima del máximo en el proceso de aumentar el cambio para cada ventana. Este es un punto clave.
| sin ventanas | con ventanas |
|---|
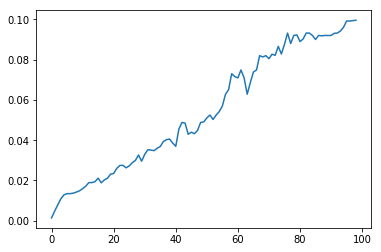 | 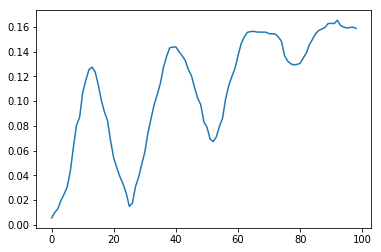 |
Fig. 3 Cambio en la mediana del brillo promedio con el cambio creciente
A continuación se muestra el código python3 con comentarios.
image = Image.open("raf_data/32.jpg").resize((600,400)) # . img = np.array(image.convert("L"), dtype=float)/255 SEARCH_WIDTH = 40 # x_opt = [0, 1] # : sh_range = range(1,100) # kmax = 0 # for x in range(0, img.shape[1]-SEARCH_WIDTH, int(SEARCH_WIDTH/2)): amax = 0 amin = 1 # for sh in sh_range: # w = img[:,x:x+SEARCH_WIDTH].mean(axis=1) aim = (pd.DataFrame(w)-pd.DataFrame(w).shift(sh))[sh:].abs().median().values[0] # aim sh if aim>amax: amax = aim amin = amax if aim<amin: amin = aim aim_k = amax/amin if aim_k>kmax: x_opt = [x, sh, w] kmax = aim_k print(' : {0}, : {1}'.format(x_opt[0], x_opt[1]))
La figura 2 marca los puntos establecidos a la distancia del turno encontrado. Como puede ver, marcan bien cada ventana. Es decir ya sabemos la altura del piso!
El algoritmo considerado encuentra buenas zonas regulares en las fachadas de varios edificios residenciales (Fig. 4).

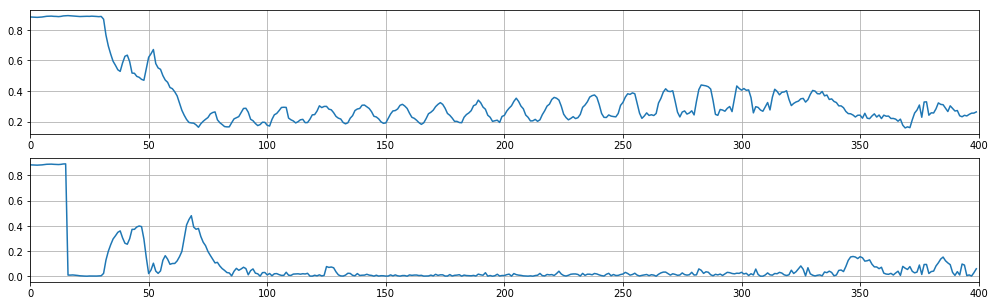

Fig. 4 Ejemplo
Paso 2. Contando el número de pisos
En este paso, comienzan las principales dificultades. Otras acciones pueden ser las siguientes:
- Estime la altura de la casa analizando la curva de diferencias de brillo promedio o usando el aprendizaje automático). Divida la altura de la casa por la altura del piso y obtenga el número de pisos.
- En la ventana que se encuentra en el primer paso, busque objetos similares a las ventanas y cuéntelos directamente, por ejemplo, en puntos específicos.
Parece natural probar el primer método primero: una vez que se conoce la altura de los pisos, queda por determinar la altura de la casa. Sin embargo, esquemas similares a los mostrados en el paso 1 resultan poco adecuados para determinar la altura de la casa, teniendo en cuenta todos los límites y transiciones posibles. En algunos casos, es posible obtener buenos ejemplos de trabajo, pero para un resultado consistentemente bueno, se necesitan enfoques que utilicen el aprendizaje automático.

Fig. 5 Determinación de la altura de la casa usando un bosque aleatorio