Uno de los elementos de más alta tecnología de las industrias aeroespaciales y militares modernas son los sistemas de navegación inercial de alta precisión (ANN). La tarea de tales sistemas, basados ​​en acelerómetros y giroscopios ópticos, es determinar las velocidades angulares, las aceleraciones de un objeto en movimiento y la orientación general del objeto en el espacio tridimensional.

Los detalles del modelado ANN es que en el campo del modelado, a menudo ocurren movimientos tanto rectilíneos como rotacionales, que afectan fuertemente el funcionamiento de estos sistemas y, en consecuencia, requieren consideración. En nuestro artículo, hablaremos brevemente sobre cuál es el efecto Sagnac y cómo los dispositivos basados ​​en él pueden investigarse numéricamente en el paquete COMSOL Multiphysics ^® .

Para una navegación conveniente, damos al principio un breve resumen del artículo:

1. ¿Qué son los giroscopios ópticos?
2. Los detalles de la contabilidad para la rotación en la simulación
3. Efecto Sagnac: base teórica
4. Modelo de interferómetro Sagnac en COMSOL Multiphysics ^®
5. Conclusión

Giroscopios ópticos y el efecto Sagnac

Quizás sea el clásico interferómetro Sagnac el que mejor demuestra la necesidad de un registro de alta precisión del movimiento no inercial del dominio de simulación.

El interferómetro Sagnac más simple consta de los siguientes componentes:

• Fuente de luz
• Un divisor de haz que dirige la luz de una fuente a lo largo de dos caminos diferentes y luego los combina
• Un conjunto de espejos (generalmente incluye dos o tres espejos)

El divisor de haz y los espejos forman una trayectoria triangular o rectangular a lo largo de la cual la luz se propaga en ambas direcciones. En este momento, el sistema de navegación en sí (así como la aeronave o nave espacial en la que está instalado) también gira a una cierta velocidad angular. Al observar la interferencia de los rayos de luz (debido al efecto Sagnac) que se propagan a lo largo de estas trayectorias, es posible determinar la velocidad angular del sistema con una precisión muy alta.

La medición de pequeñas rotaciones es vital para determinar y controlar la orientación de los objetos en las industrias modernas de defensa y espacio. Actualmente, los giroscopios con láser de anillo y fibra óptica, cuyo principio también se basa en el efecto Sagnac, son los más utilizados. Tenga en cuenta que un giroscopio láser de anillo es altamente preciso, económico y fácil de mantener, ya que, a diferencia de los giroscopios mecánicos, no contiene piezas giratorias.

Modelado de la propagación de la luz en componentes ópticos giratorios.

¿Cómo calcular la trayectoria de propagación de la luz en un sistema giratorio de espejos, prismas y divisores de haz? Para no profundizar en la teoría de la relatividad, suponga que la velocidad de rotación es mucho menor que la velocidad de la luz, pero es lo suficientemente grande como para tener que tener en cuenta la rotación. Existen al menos dos enfoques para resolver este problema:

1. Reescribe ecuaciones para la propagación de la luz en un marco de referencia no inercial
2. Rota la estructura en tiempo real cuando propagas rayos

La diferencia entre estos enfoques es que en un caso el modelo se encuentra en un marco de referencia no inercial conectado con un interferómetro móvil (opción No. 1), o en un sistema de referencia de "laboratorio" fijo en el espacio (opción No. 2). Como la segunda opción es mucho más simple de implementar, utilizaremos este enfoque para simular el interferómetro Sagnac.

El paquete COMSOL Multiphysics ^® es bastante efectivo para modelar dispositivos con una estructura móvil o deformante (que incluye el interferómetro Sagnac y un giroscopio láser de anillo) y le permite integrar y simular varios procesos físicos interdisciplinarios dentro de un solo modelo computacional.

El análisis de estructuras deformables y móviles se lleva a cabo tradicionalmente con especial cuidado, ya que se utiliza en varios campos: en el análisis de estrés térmico, la interacción de un fluido con una estructura, flujos multifásicos, así como en dispositivos de galvanoplastia, piezoeléctricos, etc. De hecho, para un trazado de rayos preciso en una estructura en movimiento, será suficiente para indicar la velocidad angular del sistema y luego comenzar un cálculo estándar basado en tecnologías ópticas geométricas .

Efecto Sagnac: base teórica

Antes de continuar con la descripción del modelo implementado en el paquete, examinemos brevemente cuál es el efecto Sagnac.

Imagine que la luz viaja estrictamente alrededor de un círculo (por ejemplo, a lo largo de un cable de fibra óptica) en dos direcciones opuestas, como se ilustra en la Fig. 1. Punto de activación del haz - $$$P_0$. La línea discontinua indica la dirección en el sentido de las agujas del reloj, y la línea continua gruesa indica la dirección en el sentido contrario. Los rayos de luz en esta configuración serán contrapuestos entre sí, ya que se propagan alrededor de la circunferencia en direcciones opuestas.

Si el anillo estuviera inmóvil, entonces las trayectorias de los rayos se cruzarían dos veces: primero en el punto opuesto del círculo y luego en el punto de partida $$$P_0$. Ahora imagine que el anillo gira en sentido antihorario alrededor de su centro con una cierta velocidad angular. Si seguimos el movimiento del punto $$$P_0$durante la propagación de la luz, veremos que un rayo que se propaga en el sentido de las agujas del reloj volverá a él cuando ya esté en una nueva posición, $$$P_1$. Cuando al punto $$$P_0$volverá un rayo que se propaga en sentido antihorario, se moverá más y estará en posición $$$P_2$. $$$P_2$ubicado a una distancia mayor de $$$P_0$que $$$P_1$porque el círculo también gira en sentido antihorario.

Fig.1. Propagación de la luz en sentido horario y antihorario a lo largo del borde de un círculo giratorio.

Obviamente, la ilustración en la Fig. 1 está significativamente escalada para mayor claridad, y en realidad la distancia entre los puntos es 10 mil millones de veces menor. Sin embargo, incluso en este caso, la diferencia en el camino óptico recorrido conduce a un cambio de fase y, en consecuencia, a la interferencia.

Sin profundizar en los cálculos teóricos (pero si son interesantes, recomendamos el siguiente trabajo clásico de Post, Evert J. "Efecto Sagnac", Reviews of Modern Physics, 39, no. 2, p. 475, 1967 ), la relación final entre la velocidad angular $$$\ Omega$y la diferencia en el camino óptico $$$\ Delta L$se puede expresar como:

$$

$$\ Delta L = {{4 \ Omega A} \ over {c_0}}$$

Donde $$$A$Es el área del círculo en consideración, y $$$c_0$Es la velocidad de la luz.

En general, el efecto Sagnac es aún más general que el ejemplo descrito anteriormente. La trayectoria de propagación de dos rayos que se aproximan puede tener cualquier forma, pero el retraso entre ellos siempre será proporcional al tamaño de la región, que está limitada por el contorno en el que se propagan los rayos. Además, este efecto también se observa en casos donde el centro de rotación no coincide con el centro del contorno.

Modelo de prueba del interferómetro Sagnac basado en el trazado de rayos ópticos

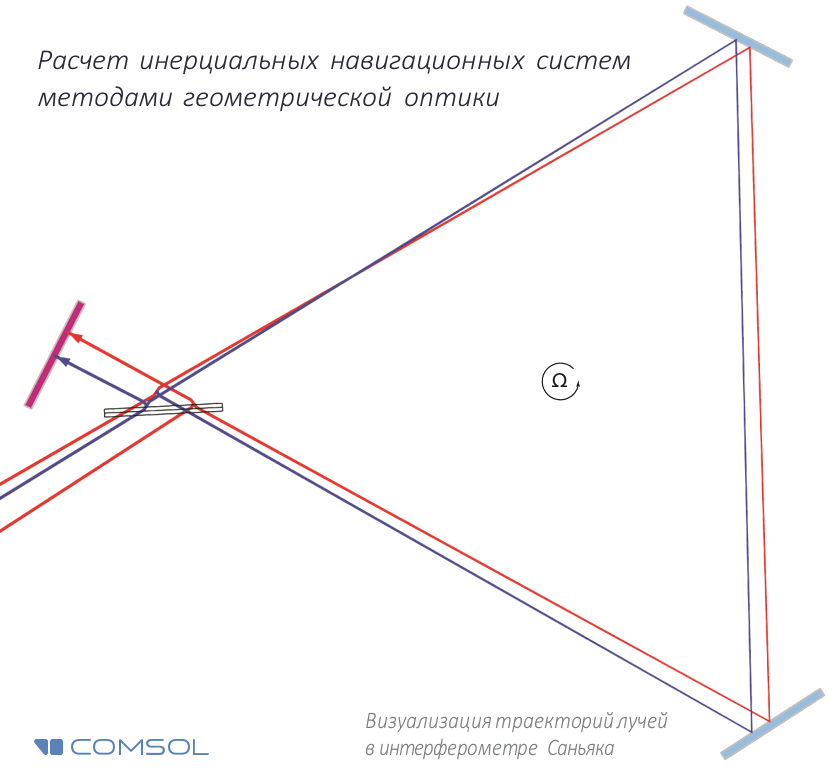
Para comprobar cómo se calculará COMSOL Multiphysics ^® $$$\ Delta L$y, por lo tanto, la sensibilidad del dispositivo, consideramos el diseño de prueba del interferómetro Sagnac, en el que la luz no se propaga alrededor de la circunferencia, sino a lo largo del perímetro del triángulo, en la parte superior del cual hay dos espejos y un divisor de haz (Fig.2).

Fig.2. Esquema del interferómetro Sagnac.

El haz inicial pasa a través de un divisor de haz, como resultado del cual se forman dos rayos de la misma intensidad. En el momento de la salida del divisor de haz, están en el mismo punto y tienen la misma fase. Dado que el sistema de espejos gira, cuando los rayos regresan al divisor de haz, sus trayectorias ópticas (y, por lo tanto, fases) son diferentes entre sí.

En la práctica, en lugar de pequeñas cantidades $$$\ Delta L$los sistemas a menudo detectan un cambio de frecuencia (o frecuencia de latido) $$$\ Delta \ nu$:

$$

$${{\ \ Delta \ nu} \ over {\ nu}} = {{\ Delta L} \ over {L}}$$

Aqui $$$L$Es la longitud efectiva del contorno a lo largo del cual se propagan los rayos, y $$$\ nu$- su frecuencia Tenga en cuenta que $$$\ Delta L$determinado directamente en el cálculo.

El proceso de trazado numérico de rayos puede automatizarse fácilmente, por ejemplo, para llevar a cabo análisis paramétricos. En la fig. La Figura 3 muestra los resultados del análisis paramétrico en un amplio rango de valores de velocidad angular, desde relativamente pequeños hasta muy grandes.

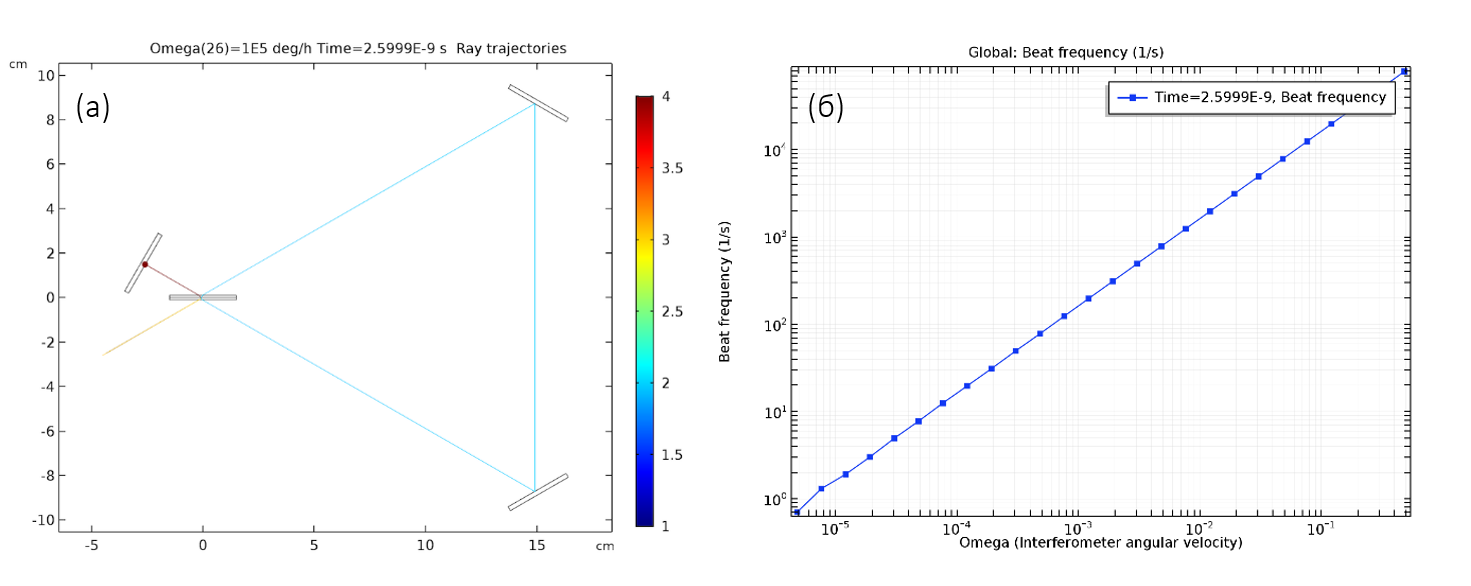
Fig.3. (a) Trayectorias de rayos en un interferómetro de prueba. Las discrepancias en la trayectoria de los dos rayos son tan insignificantes que ni siquiera se notan en el primer plano (b) La dependencia de la frecuencia de latido de la frecuencia angular de rotación del sistema.

La frecuencia de latido correspondiente está en excelente acuerdo con los valores teóricos. Al cambiar la distancia entre los espejos, se puede demostrar que la pendiente de esta línea es proporcional al área de la región triangular encerrada entre los rayos que se aproximan.

Una mirada hacia el futuro o la aplicación práctica del modelado numérico de giroscopios ópticos.

Los resultados anteriores demuestran que, al rastrear rayos en una geometría giratoria (marco) utilizando la técnica descrita, es posible calcular con alta precisión la sensibilidad de los dispositivos en función del efecto Sagnac, si la velocidad de rotación es baja en comparación con la velocidad de la luz (es decir, sin efectos relativistas). Por lo tanto, gracias a este nuevo modelo , los especialistas en modelado e ingenieros que trabajan con sistemas de orientación angular ahora tendrán una plantilla de trabajo preparada para estudiar el efecto Sagnac, que subyace al funcionamiento de los giroscopios láser de anillo.

Un lector atento probablemente preguntará acerca de la necesidad de tal simulación numérica, dado el hecho de que el efecto Sagnac se describe con precisión por la fórmula anterior. Vale la pena considerar que los ANN reales son mucho más complicados que la configuración más simple con un divisor de haz y dos espejos, discutido anteriormente. Dichos sistemas se instalan junto con otros dispositivos sensibles en un espacio limitado, se requiere un marco adicional, lo que garantiza la inmovilidad de los componentes ópticos entre sí. Además, a menudo los ANN funcionan en entornos agresivos y se ven afectados por el estrés mecánico, la temperatura y los campos electromagnéticos. Estos factores afectan el comportamiento y la sensibilidad del giroscopio, lo que requiere una consideración más detallada y exhaustiva, y no puede describirse con la misma fórmula simple.

Por lo tanto, el trazado de rayos presentado en el interferómetro Sagnac o un giroscopio láser de anillo será solo el primer paso en un análisis multifísico completo y de alta precisión de grandes sistemas ópticos. COMSOL Multiphysics ^® permite el trazado de rayos en las condiciones más realistas, en particular teniendo en cuenta el calentamiento y las deformaciones térmicas de los componentes ópticos, lo que abrirá nuevas posibilidades para una mejor comprensión y evaluación de la sensibilidad y precisión de los complejos sistemas de navegación inercial.

Información adicional

Este material se basa en los siguientes artículos:

• C. Boucher. Comprender el efecto Sagnac a través de la simulación óptica de rayos , Laser Focus World, agosto de 2018
• Simulación de un interferómetro Sagnac y un giroscopio láser de anillo utilizando métodos de óptica geométrica , blog corporativo COMSOL

Para un conocimiento más detallado de los métodos y ejemplos descritos, puede solicitar una versión demo gratuita y totalmente funcional de COMSOL Multiphysics ^® en los comentarios o mediante el enlace .

También invitamos a todos el 1 de noviembre al evento principal para los usuarios actuales y futuros de COMSOL: el Día de COMSOL en Moscú .