Pasó un compromiso: ¡puedes casarte!

Introduccion

El método de elementos finitos (FEM o FEM, tienen en el extranjero) entró firmemente en la práctica de los cálculos de ingeniería en el diseño de sistemas complejos. En gran medida, esto se relaciona con los cálculos de resistencia de la mecánica. La aplicación de este método, implementado por el software apropiado, acorta significativamente el ciclo de desarrollo del dispositivo final, eliminando la masa de comprobaciones experimentales necesarias cuando se utilizan cálculos clásicos basados ​​en los métodos de sopromat y mecánica estructural. Hasta la fecha, se ha desarrollado una gran cantidad de software de aplicación que implementa FEM. A la vanguardia está el poderoso ANSYS, a los lados y a una distancia honoraria: sistemas CAD con un módulo FEM incorporado (SolidWorks, Siemens NX, Creo Parametric, Compass 3D).

CalculiX es fuerte, pero difícil e incomprensible. Vamos a arreglar esto?



Naturalmente, el FEM ha penetrado en el campo de la educación: para usarlo en tareas reales, se necesita la capacitación de especialistas relevantes. En las capitales, en las grandes universidades técnicas, la situación en esta área es más o menos normal, y en nuestra región se usa el mismo ANSYS, por ejemplo, en el Departamento de Teoría de la Elasticidad de la Universidad Federal del Sur. Pero en la periferia, en universidades estrechamente especializadas y no ricas, la situación es deplorable. Y es simple: ANSYS cuesta alrededor de 2 millones de rublos para un lugar de trabajo, y se requiere más de un lugar. Desafortunadamente, no todas las universidades pueden pagar 30-40 millones para organizar una clase de computación para enseñar el uso de FEM.

Una de las alternativas es el uso de software libre en el proceso educativo. Afortunadamente, dicho software está disponible. Sin embargo, prácticamente no hay materiales en ruso sobre su uso. Al corregir esta situación, dedicaré este artículo a la introducción de CalculiX , un paquete de software abierto y gratuito diseñado para resolver problemas tridimensionales lineales y no lineales de la mecánica de un cuerpo sólido deformable y mecánica de fluidos y gases utilizando el método de elementos finitos.

1. Qué es CalculiX y dónde obtenerlo. Instalación de Windows

El paquete CalculiX es un conjunto de utilidades de consola, que incluye un preprocesador para preparar datos de origen, un solucionador de FEM y un postprocesador para procesar los resultados. CalculiX se utiliza de forma independiente y como parte de otros productos, entre los cuales FreeCAD está ganando impulso. Otra pregunta es que CalculiX todavía es poco conocido en nuestro país, lo cual se afirma directamente en el único artículo sobre este recurso .

Específicamente mencionaré el siguiente material con respecto al trabajo en Windows, como las instituciones educativas más comunes y utilizadas. Además, el uso de muchos programas gratuitos en él es un dolor abierto.

Si toma el paquete de Windows del sitio web oficial de CalculiX, no queda completamente claro qué hacer a continuación. Junto con la documentación en inglés, pone fin a este producto para muchos y luego se traduce en comentarios venenosos sobre la imposibilidad de su uso. Y en parte esto es cierto: el umbral de entrada es realmente alto. Pero aún así lo intentaremos.

Hay una serie de compilaciones no oficiales, relativamente novatas y amigables de este milagro para Windows, entre ellas bConverged CalculiX para Windows . Descargamos el kit de distribución desde aquí , lo desempaquetamos y lo instalamos utilizando el método estándar "más, más ...". La instalación, por lo tanto, no constituye un misterio especial y es bastante accesible para un usuario inexperto. Como el entorno de trabajo principal, este paquete utiliza el editor de texto SciTE, que integra las llamadas a los componentes de CalculiX, así como la posibilidad de entrada interactiva de comandos y se ve así (hacer clic).

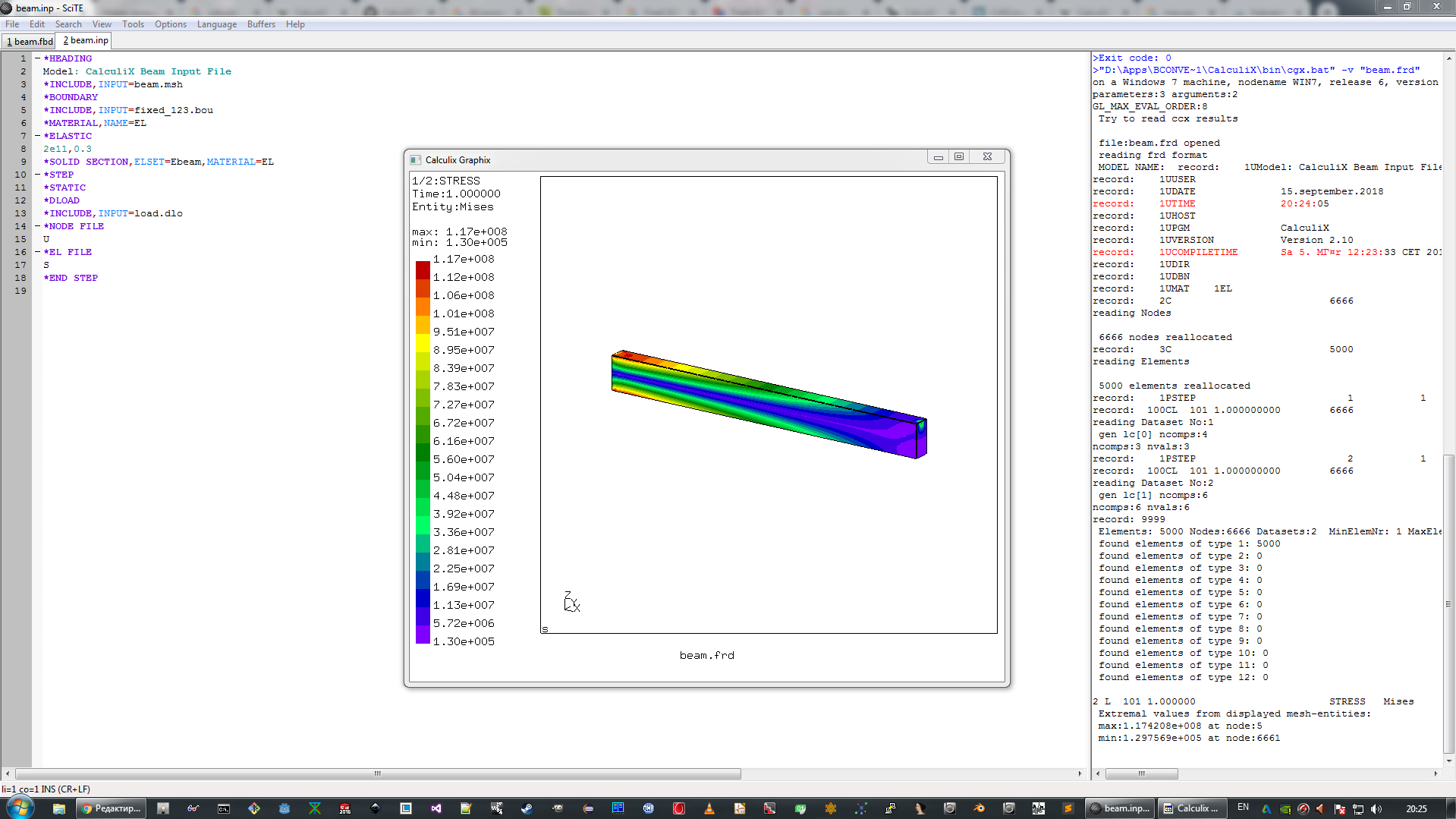
2. El problema de la flexión de vigas y su solución analítica utilizando métodos de sopromat

Consideremos un problema simple de un alumno: doblar una viga de acero, un extremo del cual está apretado, y la fuerza vertical F se aplica al otro.



Los parámetros del problema son los siguientes: F = 10 kN; l = 1 m es la longitud de la viga; h = 0.1 myb = 0.05 m son las dimensiones de la sección transversal. Para simplificar, no tendremos en cuenta el peso de la viga, ya que, con un peso de la viga de 39 kg, es significativamente menor que la carga aplicada. Encontramos el esfuerzo normal máximo en la sección de la viga y también calculamos la desviación de la viga debido a la deformación de flexión.

Cualquier estudiante que no haya omitido un compromiso resolverá fácilmente dicho problema. Para no avergonzar a los nobles dons, envolveré todos los detalles de la decisión en un spoiler


Para aquellos que son demasiado flojos para mirar debajo del spoiler, les daré la respuesta inmediata al problema: el voltaje normal máximo en la sección del haz $$$\ sigma_x = 119$ MPa, y la deflexión máxima es de 3.97 mm. Estas cifras se dan para una comparación posterior con lo que nos dará el procedimiento para resolver este problema en CalculiX.

3. Preparación de geometría y grilla computacional.

En primer lugar, debe ingresar datos geométricos sobre la parte en cuestión en CalculiX. Sí, es posible exportar geometría desde CAD, como se hace en el mismo ANSYS, pero pasaremos por la tortura e ingresaremos la geometría manualmente. Abra el editor SciTE del kit bConverged y escriba el siguiente texto

pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0

Guarde el archivo con el nombre beam.fbd y presione F10 para iniciar el preprocesamiento. Veremos algo como lo siguiente



El comando pnt crea un punto en el espacio con las coordenadas dadas y su sintaxis es la siguiente

pnt [ ] [x] [y] [z]

Ahora conecte estos puntos con líneas, agregando el siguiente texto al archivo

line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25

habiendo recibido después de presionar F10 la siguiente imagen



El equipo

line [ ] [ 1] [ 2] [ ]

crea una línea que conecta los puntos indicados en ella, agregando puntos intermedios que dividen la línea en un número específico de segmentos (en nuestro caso, 25 para cada línea). Esto será útil más tarde para la generación de la red. Ahora haz la finta con nuestros oídos

seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10

Primer equipo

seta [ ] [ 1] ... [ N]

combina varios objetos en un conjunto con el nombre dado. De hecho, esto es un análogo de la agrupación de objetos. Siguiente comando

swep [ ] [ ] [ ] [, ] []

Mueve el conjunto de objetos seleccionado para formar un nuevo conjunto. Los objetos móviles se copian. En este caso, el movimiento de puntos forma líneas, el movimiento de líneas - superficies, el movimiento de superficies - volúmenes continuos. En nuestro caso, cambiamos el conjunto de líneas a lo largo del eje Z en 0.1 metros, mientras que las líneas resultantes se dividen en 10 segmentos. Presionamos F10 ... er, ¿y qué es?



Ghm, una pantalla en blanco ... Es fácil de arreglar, solo agrega líneas al final del guión

plot pa all
plus la all

Estos comandos le indican que dibuje todos los puntos (pa) y agregue todas las líneas (la) a la pantalla, después de lo cual obtenemos este resultado



Ahora creemos superficies basadas en el conjunto de líneas que creamos

seta surfaces s A001 A002 A003 A004

agregando la visualización de estas superficies al final del guión

plus sa all




Ahora realizaremos otro cambio, ahora a lo largo del eje Y en 0.05 metros, desarrollando todas las líneas formadas por el desplazamiento en 5 segmentos.

swep surfaces swepsurface tra 0.0 0.05 0.0 5

Consigue algo en el espíritu



La imagen resultante se puede girar manteniendo presionado el botón izquierdo del mouse y eliminando la visualización de puntos y líneas, veremos algo inteligible



Sí ... CalculiX está lejos de los conceptos visuales habituales familiares para el usuario masivo, pero, sin embargo, construimos la geometría de nuestra viga.

Geometría, geometría, pero para la generación de mallas haremos el siguiente movimiento: eliminar todos los comandos de trazado y más y envolver el código de generación de geometría en comandos seto y setc, como este

seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam

Este par de comandos combina toda la geometría creada en un determinado bloque de geometría con la viga de nombre. Ahora este grupo geométrico se puede omitir a través de la generación de malla, especificando después de todo el código de comando anterior

elty beam he8
mesh beam

- Genera una cuadrícula que consiste en paralelepípedos (he8) basados ​​en una geometría llamada viga. Ahora imprima la malla generada en un archivo

send beam abq

- salida de malla a un archivo llamado beam.msh en el formato del paquete ABAQUS FEM (existe un paquete propietario de cálculos FEM y CalculiX comprende su formato)



Por lo tanto, se genera la cuadrícula, puede mirar en el archivo beam.msh y ver algo como esto allí

*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34

Aparentemente, esta es una lista de vértices de los elementos de la cuadrícula con sus coordenadas, seguida de una lista de caras. Para hacer que todo esto se vea más hermoso, utilizamos el modo interactivo CalculiX. Para hacer esto, dejando la ventana gráfica activa , ingrese los siguientes comandos secuencialmente

plot f beam

- Mostrar todas las caras de la geometría

view edge off

- apague la pantalla de bordes

view elem

- activar la visualización de elementos de cuadrícula. Completamos la entrada de cada comando presionando Enter, los comandos ingresados ​​se muestran en la ventana SciTE en la parte inferior derecha, así



Sí, no puede llamarlo súper conveniente, pero de todos modos obtenemos una imagen de la malla generada.



Observo que todos los puntos intermedios que se crearon al crear la geometría se convirtieron en nodos de malla. Por lo tanto, obtuvimos una cuadrícula hexagonal que mide 100 x 10 x 5 nodos, con un tamaño de borde de elemento de 10 mm. El archivo beam.fbd que creamos describe la geometría del problema y el proceso de creación de la malla.

4. Establecer límites

Un paso importante en la aplicación del FEM es establecer restricciones en el desplazamiento de puntos estructurales, es decir, tener en cuenta las restricciones impuestas sobre él. En nuestro caso, uno de los extremos de la viga está pellizcado, y se puede suponer que uno de sus extremos está completamente estacionario. Necesitamos decirle al solucionador qué nodos de la malla FE están inmóviles. Presionamos F10 cuando el archivo beam.fbd está abierto, espere a que aparezca la ventana con la imagen de la viga



En modo interactivo, ingrese el comando
rot -y
plot n beam

El primer equipo despliega el modelo para que el eje Y se aleje de nosotros, el segundo incluye nodos de dibujo (n) de la malla FE. Moviendo el modelo (sosteniendo el botón derecho del mouse) y escalando la imagen (sosteniendo la rueda del mouse) obtenemos esta imagen



Ahora necesitamos seleccionar todos los nodos que queremos definir como fijos. Para hacer esto, nuevamente usamos el modo de entrada de datos interactivos. Reclutamos un equipo

qadd fixed

que comienza a crear un conjunto de nodos llamados fijos. El cursor en la ventana gráfica cambia al modo de selección de elementos: se muestra en forma de flecha con un cuadrado pequeño. Pon el cursor así



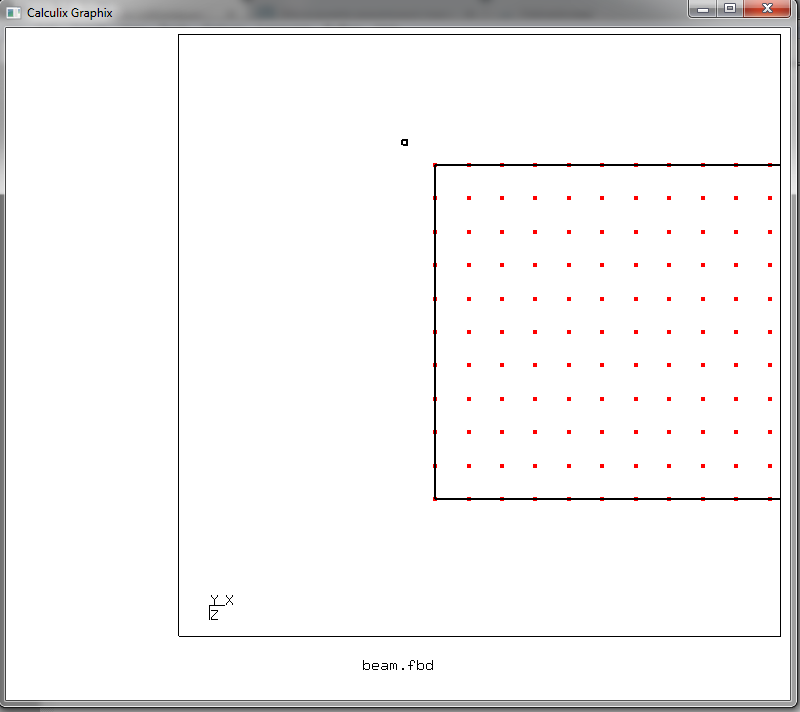
y presione la tecla r. Y luego ponemos el cursor así



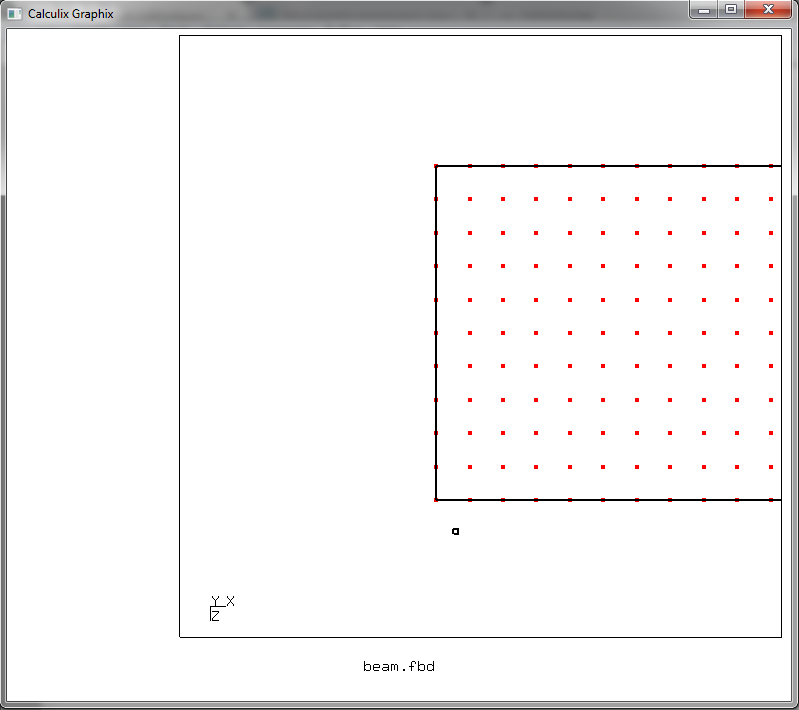
y presione r nuevamente. Por lo tanto, formamos un área de selección de forma rectangular, cuya diagonal se establece mediante las posiciones del cursor marcadas presionando r. Seleccionamos con este rectángulo los nodos que necesitamos tendidos en el extremo de la viga



presione ay luego presione n, resaltando los nodos marcados. Aparecerá un paño en la ventana de la consola con una lista de nodos seleccionados (se puede hacer clic en la imagen)



Ingrese q para salir del modo de selección y comando

plus n fixed g

para mostrar los nodos del grupo fijo en verde (g). Ahora podemos ver qué nodos se incluirán en la condición de fijación.



Ahora debemos descargar estos nodos como un archivo de restricción, que posteriormente se alimenta a la entrada del solucionador. Para hacer esto, escriba el comando

send fixed abq spc 123

- descargue un grupo de nodos fijos en forma de un archivo de restricción en el formato ABAQUS (abq), restringiendo el movimiento de todos los nodos del grupo en los tres grados de libertad (1 - eje X, 2 - eje Y, 3 - eje Z). Como resultado, se forma el archivo fixed_123.bou, con los siguientes contenidos

** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.


- de hecho, esta es una enumeración de todos los nodos y el número de grado de libertad por el cual el movimiento de un nodo dado es limitado.

5. Asignación de cargas.

Después de asegurar nuestra viga, intentaremos cargarla. Encienda nuevamente la visualización de caras y elementos

plot f beam
view edge off
view elem

Oriente la imagen para que podamos ver la parte superior del extremo suelto de la viga.



Cambiemos al modo de selección de objetos.

qadd load

Coloque el cursor en la cara deseada y presione f



La cara se resalta en púrpura y aparece una descripción en la ventana de la consola que se agrega al conjunto de carga.

qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300

Presione a para finalizar la formación del conjunto, presione q para salir del modo de selección. Aplicamos una presión a la cara seleccionada que da una fuerza resultante de 10,000 N. Es fácil calcular que el área de la cara seleccionada es 1 cm ² , lo que significa que la presión deseada es 10 ⁸ Pa. Establezca esta carga con el comando

send load abq pres 1e8

- muestra la carga en el archivo load.dlo en formato ABAQUS. El archivo se ve así

** Pressure based on load
3873, P6, 100000000.000000

Se indica el número del elemento de malla, su cara y el valor de presión en esta cara. Por lo tanto, la preparación de los datos iniciales puede considerarse completada.

6. Descripción de los datos de entrada y el lanzamiento del solucionador.

Todos esos datos, la cuadrícula, las limitaciones y las cargas, ahora deben extraerse a la entrada del solucionador FEM, para lo cual formamos un archivo de entrada de este tipo

beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Explicaré con más detalle qué es qué. Primera sección del archivo

*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh

establece la descripción de la tarea e incluye un archivo con el CE-mesh beam.msh. La siguiente sección forma las condiciones de contorno: aquellas relaciones que definimos en el archivo fixed_123.bou

*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou


No debemos olvidarnos del material que establecemos como elástico, determinando su módulo de Young y la relación de Poisson. Tomamos los valores promedio para aceros estructurales

*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL

La última sección establece el tipo de tarea: el cálculo de la carga estática y las cargas del archivo load.dlo que son

*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Después de verificar que tenemos una pestaña en SciTE con el archivo beam.inp, presione Ctrl + F10, iniciando así el solucionador. Recibimos un escape que nos dice que CalculiX ha calculado algo para nosotros allí. Escape, para no abarrotar el texto que traigo debajo del spoiler

7. Postprocesamiento y análisis de decisiones

Los resultados obtenidos por el solucionador requieren procesamiento por parte del postprocesador. Para llamarlo, presione Mayús + F10 y obtenga una ventana gráfica con la imagen de la viga. Haga clic en el lado izquierdo de esta ventana, fuera del marco con la imagen de la viga y obtenga el menú



Lo que nos interesa Tensiones en las secciones de la viga: seleccione Conjuntos de datos -> ESTRÉS. El menú desaparecerá, pero lo llamamos nuevamente y seleccionamos Conjuntos de datos -> Entidades -> Mises. Como resultado, se activa el modo de tensión equivalente de von Mises.



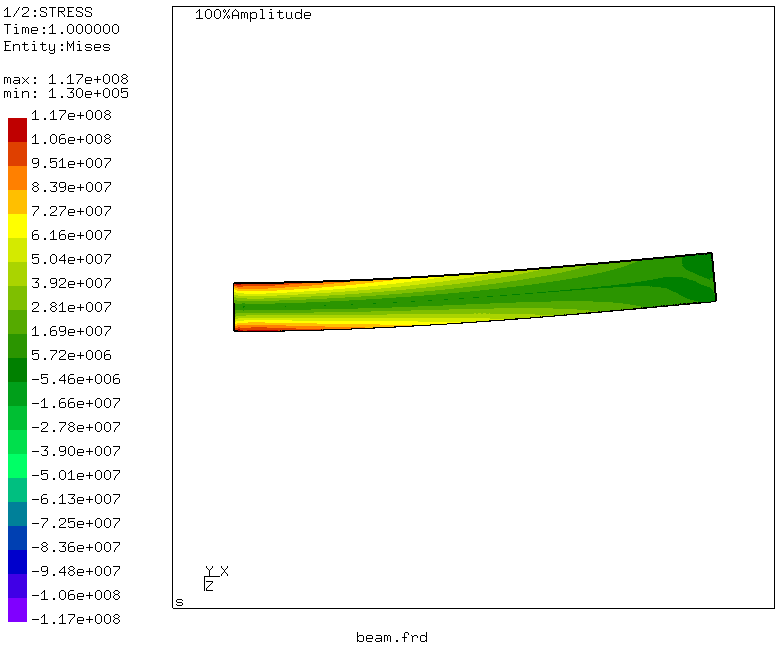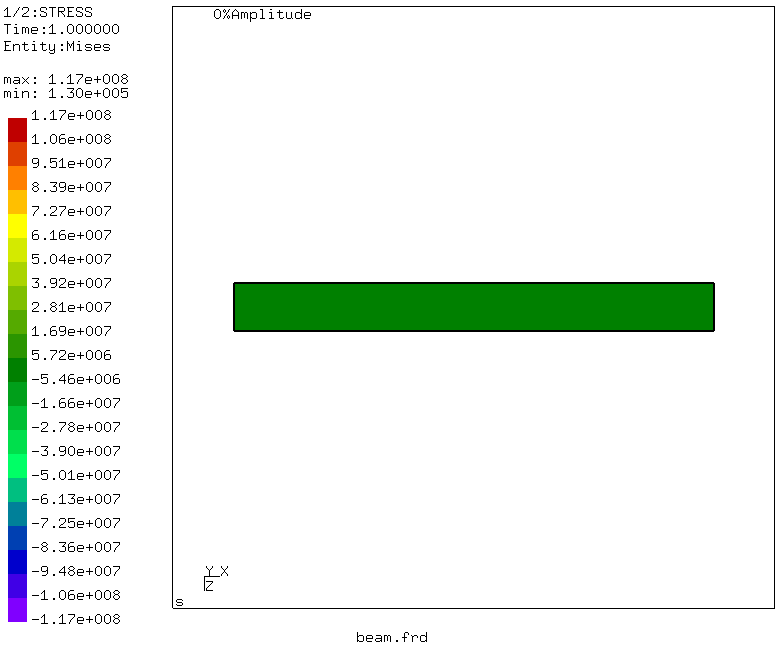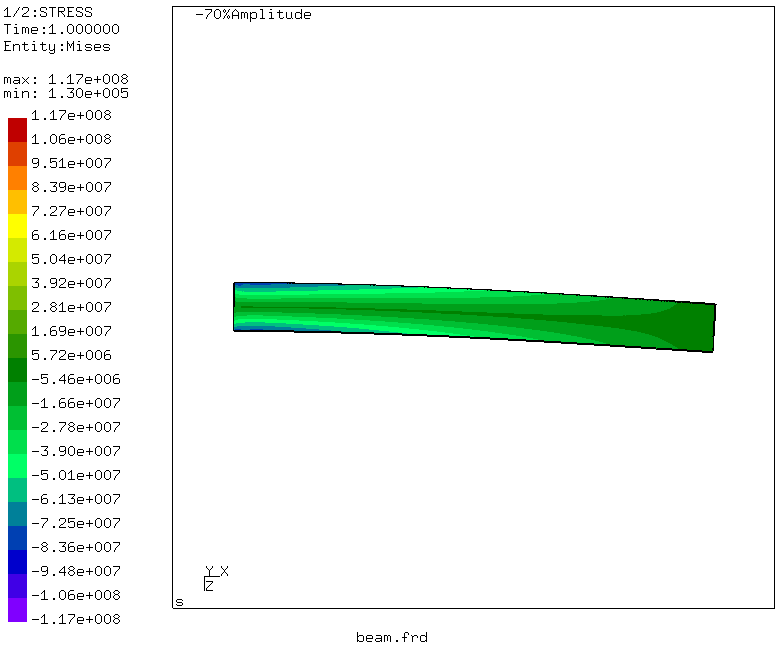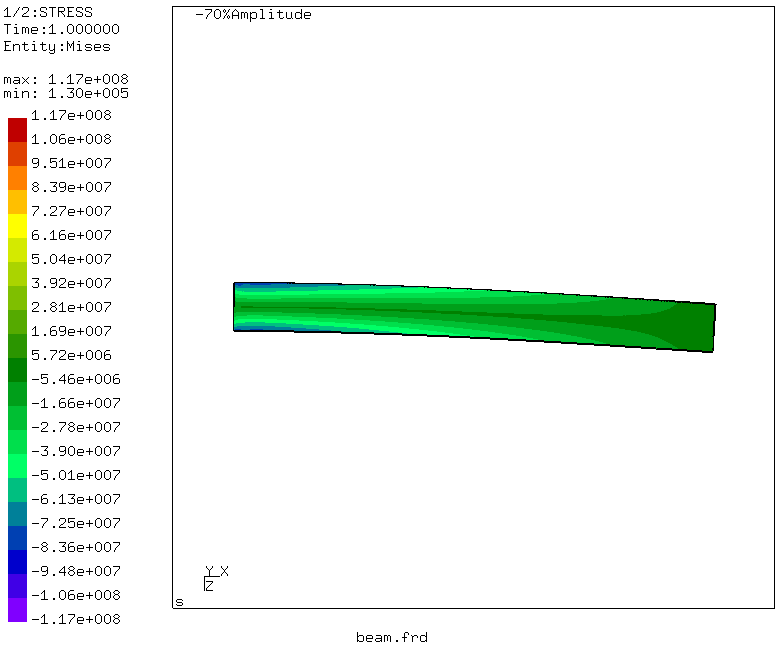
Entonces, ¡el momento de la verdad! El esfuerzo equivalente máximo en la sección de la viga es de 117 MPa, que difiere ligeramente del resultado del compromiso. Pero! Al resolver el problema del sopromat, no tomamos en cuenta las tensiones tangenciales durante la flexión y el corte, sino que calculamos solo las tensiones normales de la flexión. ¿Qué pasará con la desviación? Vaya al menú: Conjuntos de datos -> DISP y Conjuntos de datos -> Entidades -> D3



¡Observamos que el desplazamiento máximo corresponde al extremo cargado de la viga y es igual a 3.96 milímetros! Magnífico y se correlaciona con nuestro cálculo utilizando la integral de Mohr.

Mediante simples manipulaciones, que se pueden leer aquí , también se genera una animación de las deformaciones del haz.

Sacar conclusiones

"Uh, amigo, espera un minuto, ¿qué sigue?" Hmm, el hombre no puede incluir en un artículo toda la variedad de problemas que surgen al mencionar el FEM en general, y CalculiX en particular. El artículo resultó ser voluminoso y bastante aburrido. Y su propósito es explicar dos cosas en un lenguaje inteligible:

1. El código abierto no pasó por el software de análisis FEM
2. Estudiar y usar este software no es tan difícil como podría parecer a primera vista

¿Suficiente para un artículo de revisión? Yo creo que si. Al preparar el artículo, se utilizaron las siguientes fuentes:

1. Calculix FEA Beam : sirvió de base para todo el material presentado. Dado que la experiencia adquirida por el autor se agrega aquí y todo el código fue escrito por él durante la redacción del artículo, esta no es una traducción, es decir, un tutorial en ruso
2. Manual oficial de CalculiX

El código de muestra está disponible en Gitlab .

En conclusión, observo: no soy fuerte, no tuve un compromiso en la universidad. Un poco más tarde, la vida (¡y el amor!) Me obligó a conocer sus fundamentos. Entonces, los errores, tal vez, están presentes en el texto, sobre el cual estoy esperando comentarios maliciosos y prometo tener en cuenta todos los comentarios.

Gracias por su atencion!