Números de punto flotante más salvajes del oeste

En el proceso de implementación de un "lector", surgió un problema con una mayor precisión de los cálculos. El algoritmo de cálculo funcionó rápidamente en números de punto flotante estándar, pero cuando se conectaron bibliotecas para realizar cálculos precisos, todo comenzó a ralentizarse enormemente. En este artículo, consideraremos algoritmos para expandir números de punto flotante utilizando un enfoque de múltiples componentes, debido a lo cual fue posible lograr la aceleración, ya que la aritmética flotante se implementa en un chip cp. Este enfoque será útil para un cálculo más preciso de la derivada numérica, inversión de matriz, recorte de polígono u otros problemas geométricos. Por lo tanto, es posible emular flotante de 64 bits en tarjetas de video que no las admiten.

Introduccion

Como Nikluas Wirth nos legó para mantener los números 0 y 1, los almacenamos en ellos. ¿Y es que los humanos viven en el sistema decimal, y los números aparentemente ordinarios 0.1 y 0.3 no son representables en el sistema binario por una fracción finita? Experimentamos un choque cultural cuando hacemos cálculos sobre ellos. Por supuesto, se están intentando crear bibliotecas para procesadores basados ​​en el sistema decimal e IEEE incluso tiene formatos estandarizados.

Pero por ahora, tenemos en cuenta el almacenamiento binario en todas partes y hacemos todos los cálculos de dinero con bibliotecas para cálculos exactos, como el número de referencia, lo que conduce a la pérdida de rendimiento. Los asiáticos consideran la criptografía, y en los procesadores hay muy poco espacio para esta aritmética decimal, dicen los especialistas en marketing. Por lo tanto, un enfoque multicomponente, cuando un número se almacena en forma de una suma de números no transformada, es un truco conveniente y una esfera en desarrollo activo en el campo de la informática teórica. Aunque Decker todavía aprendió a multiplicar correctamente, sin pérdida de precisión, en 1971, las bibliotecas listas para usar aparecieron mucho más tarde (MPFR, QD) y no en todos los idiomas, aparentemente porque no todos admitían estándares IEEE, pero pruebas rigurosas de error de cálculo incluso más tarde, por ejemplo en 2017 para aritmética de doble palabra.

Aritmética de doble palabra

Cual es el punto? En tiempos de barba, cuando no había estándares para números flotantes, para evitar problemas con la implementación del redondeo, Møller se le ocurrió, y Knuth luego demostró que hay una suma libre de errores. Corriendo de esta manera

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

En este algoritmo, se suponía que si $$$| a | > | b |$, entonces su suma exacta se puede representar como la suma de dos números $$$s + e$y puede almacenarlos en pares para cálculos posteriores, y la resta se reduce a la suma con un número negativo.



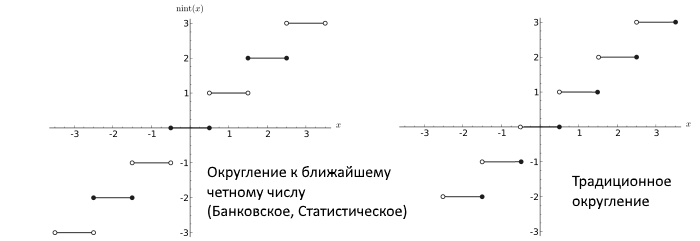
Posteriormente, Dekker demostró que si se usan números de punto flotante que usan el redondeo al número par más cercano (enlaces de redondeo a más cercano a par, que generalmente es un procedimiento correcto que no conduce a grandes errores en el proceso de cálculos largos y el estándar IEEE), entonces hay un algoritmo de multiplicación sin errores.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

donde split () es el algoritmo del Sr. Weltkamp para dividir un número

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

usando constante $$$C = 2 ^ s + 1$lo que equivale a un poco más de la mitad de la longitud de la mantisa, lo que no conduce a un desbordamiento de números en el proceso de multiplicación y divide la mantisa en dos mitades. Por ejemplo, con una longitud de palabra de 64 bits, la longitud de la mantisa es 53 y luego s = 27.



De esta manera, Dekker proporcionó el conjunto casi completo necesario para computar en aritmética de doble palabra. Como allí también se indicó cómo multiplicar, dividir y cuadrar dos números de doble palabra.

Su algoritmo quickTwoSum para sumar dos palabras dobles estaba en todas partes "en línea", y se utilizó el cheque $$$| a | > | b |$. En los procesadores modernos, como se describe en [4], es más barato usar operaciones adicionales con números que ramificar el algoritmo. Por lo tanto, el siguiente algoritmo ahora es más apropiado para agregar dos números de una sola palabra

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

Y entonces esta es la suma y multiplicación de números de doble palabra.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

En términos generales, la lista más completa y precisa de algoritmos para aritmética de doble palabra, límites de error teóricos e implementación práctica se describe en el enlace [3] de 2017. Por lo tanto, si está interesado, recomiendo ir directamente allí. En general, se proporciona un algoritmo para palabra cuádruple en [6], y en [5] para una extensión multicomponente de longitud arbitraria. Solo allí, después de cada operación, se utiliza el proceso de renormalización, que no siempre es óptimo para tamaños pequeños, y la precisión de los cálculos en QD no está estrictamente definida. En general, vale la pena pensar en los límites de aplicabilidad de estos enfoques, por supuesto.

Historias de terror javascript-a. Comparación de decimal.js vs bignumber.js vs big.js.

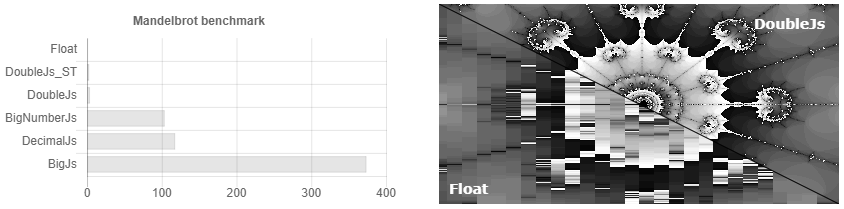
Sucedió que casi todas las bibliotecas para cálculos exactos en js fueron escritas por una persona. Se crea la ilusión de elección, aunque son casi todos iguales. Además, la documentación no indica explícitamente que si no redondea números después de cada operación de multiplicación / división, entonces el tamaño de su número se duplicará todo el tiempo, y la complejidad del algoritmo puede convertirse en una fácil en x3500. Por ejemplo, una comparación de su tiempo de cálculo podría verse así si no redondea los números.



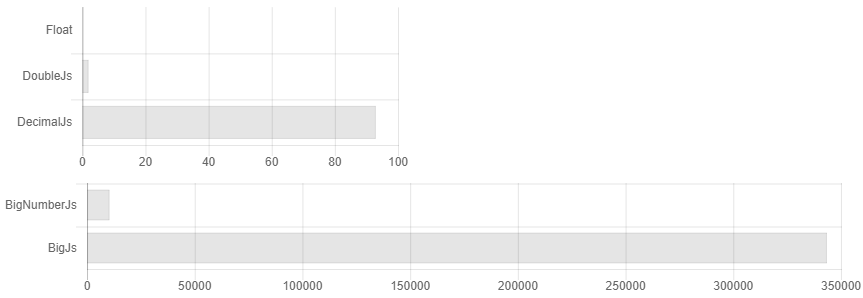
Es decir, establece la precisión en 32 decimales y ... ¡Vaya! Ya tiene 64 dígitos, 128. ¡Pensamos con mucha precisión! 256, 512 ... ¡Pero configuré 32! .. 1024, 2048 ... Algo como esto aparece sobrecarga 3.500 veces. La documentación indica que si tiene cálculos científicos, entonces probablemente decimal.js sea mejor para usted. Aunque, de hecho, si redondeas periódicamente, para cálculos científicos, Bignumber.js funciona un poco más rápido (ver Fig. 1). ¿Quién necesita contar las centésimas de centavo si no se pueden dar en cambio? ¿Hay algún caso en el que necesite almacenar más números indicados y no pueda salir con algunos caracteres adicionales? ¿Cómo toma el seno de un número tan monstruoso, cuando nadie conoce la precisión estricta de la convergencia de la serie Taylor para números arbitrarios? En general, no existen sospechas infundadas de que es posible aumentar la velocidad de cálculo allí, utilizando algoritmos de multiplicación de Schoenhage-Strassen y encontrando el seno con cálculos Cordic, por ejemplo.

Double.js

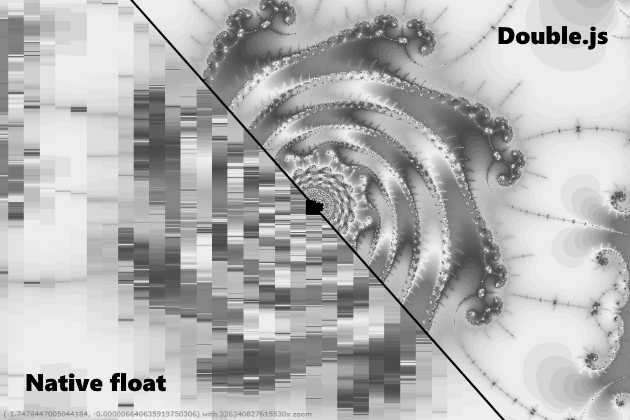
Me gustaría decir, por supuesto, que Double.js cuenta de forma rápida y precisa. Pero esto no es del todo cierto, es decir, es 10 veces más rápido de lo que considera, pero no siempre es preciso. Por ejemplo, 0.3-0.1 puede procesar, pasando al doble almacenamiento y viceversa. Pero el número Pi se puede resolver con una precisión doble de casi 32 dígitos y no funciona. Se genera un error el día 16, como si ocurriera un desbordamiento. En general, insto a la comunidad js a trabajar juntos para tratar de resolver el problema del análisis, ya que estoy atascado. Traté de analizar digitalmente y dividir en doble precisión, como en QD, dividir en lotes de 16 dígitos y dividir en doble precisión, dividir la mantisa usando Big.js como en una de las librerías de Julia. Ahora peco por un error en .parseFloat (), ya que los estándares IEEE con redondeo al número entero más cercano son compatibles incluso con ECMAScript 1. Aunque, por supuesto, puede intentar vincular el búfer binario y observar cada 0 y 1. En general, si puede resolver este problema, entonces entonces será posible hacer cálculos con precisión arbitraria con aceleración en x10-x20 desde bignumber.js. Sin embargo, muchos Mandelbrot ya ofrecen calidad, y puede usarlo para tareas geométricas.

Un año después, regresé aquí y aún solucioné un problema con el análisis. El problema estaba solo en una precisión insuficiente, cuando se multiplicaba por 10 ^ (- n). Todos los algoritmos se han revisado desde cero y ahora se ejecutan con una precisión y velocidad alarmantes.



Aquí hay un enlace a la biblioteca , hay un punto de referencia interactivo y un sandbox donde puedes jugar con él.

Fuentes utilizadas

1. O. Møller. Cuasi doble precisión en aritmética de coma flotante. 1965.
2. Theodorus Dekker. Una técnica de punto flotante para extender la precisión disponible , 1971. [ Visor ]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Límites de error estrictos y rigurosos para bloques de construcción básicos de aritmética de doble palabra , 2017. [ PDF ]
4. Muller, J.-M. Brisebarre, N. de Dinechin, etc. Manual de aritmética de coma flotante, Capítulo 14, 2010.
5. Jonathan Shewchuk. Predicados geométricos adaptativos de coma flotante robustos , 1964. [ PDF ]
6. Yozo Hida, Xiaoye Li, David Bailey. Biblioteca para aritmética doble-doble y cuádruple-doble , 2000. [ PDF ]