De hecho, él es el más. Pero lo primero es lo primero.
Declaración del problema.
Domino Python, resuelvo todo en Codewars. Me encuentro con una tarea bien conocida sobre un rascacielos y huevos. La única diferencia es que los datos de origen no son 100 pisos y 2 huevos, sino un poco más.
Dado: N huevos, M intenta tirarlos, rascacielos sin fin.
Definir: el piso máximo desde el que puedes lanzar un huevo sin romperse. Los huevos son esféricos en el vacío y, si uno de ellos no se rompe, cayendo, por ejemplo, del piso 99, los otros también resistirán una caída de todos los pisos de menos de una centésima.
0 <= N, M <= 20,000.
El tiempo de ejecución de dos docenas de pruebas es de 12 segundos.
Busca una solución
Necesitamos escribir una altura de función (n, m), que devolverá el número de piso para el n, m dado. Como se mencionará muy a menudo, y cada vez que escriba pereza de "altura", en todas partes, excepto en el código, lo designaré como f (n, m).
Comencemos con ceros. Obviamente, si no hay huevos o intentos de tirarlos, entonces no se puede determinar nada y la respuesta será cero.
f (0, m) = 0, f (n, 0) = 0.Supongamos que hay un huevo y hay 10 intentos. Puedes arriesgarlo todo y tirarlo directamente desde el piso cien, pero en caso de falla, no podrás determinar nada más, por lo que es más lógico comenzar desde el primer piso y subir un piso después de cada lanzamiento, hasta que termine el intento o el huevo. El máximo donde puede llegar si el huevo no falla es el piso número 10.
f (1, m) = mToma el segundo huevo, intenta nuevamente 10. Ahora, ¿puedes arriesgarte con una centésima? Si se rompe, habrá uno más y 9 intentos, al menos 9 pisos podrán pasar. Entonces, ¿quizás necesites arriesgarte no desde la centésima, sino desde la décima? Es lógico. Luego, si tiene éxito, quedarán 2 huevos y 9 intentos. Por analogía, ahora necesita subir otros 9 pisos. Con una serie de éxitos: otros 8, 7, 6, 5, 4, 3, 2 y 1. Total, estamos en el piso 55 con dos huevos enteros y sin intentarlo. La respuesta es la suma de los primeros M miembros de la progresión aritmética con el primer miembro 1 y el paso 1.
f (2, m) = (m * m + m) / 2 . También está claro que en cada paso se llamó a la función f (1, m), pero esto aún no es exacto.
Continuar con tres huevos y diez intentos. En caso de un primer lanzamiento fallido, los pisos cubiertos por 2 huevos y 9 intentos se cubrirán desde abajo, lo que significa que el primer lanzamiento debe hacerse desde el piso f (2, 9) + 1. Luego, si tiene éxito, tenemos 3 huevos y 9 intentos . Y para el segundo intento debes subir otro f (2.8) + 1 pisos. Y así sucesivamente, hasta que queden 3 huevos y 3 intentos en las manos. Y luego es hora de distraerse considerando casos con N = M, cuando hay tantos huevos como intentos.
Y al mismo tiempo aquellos cuando hay más huevos.Pero aquí todo es obvio: los huevos más allá de los que se rompen no serán útiles para nosotros, incluso si cada lanzamiento no tiene éxito. f (n, m) = f (m, m) si n> m . Y en general, 3 huevos, 3 tiros. Si el primer huevo se rompe, puede verificar f (2, 2) pisos hasta el fondo, y si no se rompe, entonces f (3,2) pisos hacia arriba, es decir, el mismo f (2, 2). Total f (3, 3) = 2 * f (2, 2) + 1 = 7. Y f (4, 4), por analogía, consistirá en dos f (3, 3) y uno, y será 15. Todos se parece a las potencias de dos, y escribimos: f (m, m) = 2 ^ m - 1 .
Parece una búsqueda binaria en el mundo físico: comenzamos desde el piso número 2 ^ (m-1), en caso de éxito subimos 2 ^ (m-2) pisos hacia arriba, y en caso de falla, bajamos tanto, y así, hasta que se acaben los intentos. En nuestro caso, nos levantamos todo el tiempo.
Volvamos a f (3, 10). De hecho, en cada paso todo se reduce a la suma f (2, m-1), el número de pisos que se puede determinar en caso de falla, unidades yf (3, m-1), el número de pisos que se pueden determinar en caso de éxito. Y queda claro que debido al aumento en el número de huevos e intentos, es poco probable que algo cambie.
f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . Y esta es una fórmula universal que se puede implementar en código.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)
Por supuesto, anteriormente pisé el rastrillo de funciones recursivas no memorables y descubrí que f (10, 40) tarda casi 40 segundos con el número de llamadas en sí mismo: 97806983. Pero la memoria también se guarda solo en los intervalos iniciales. Si f (200,400) se ejecuta en 0,8 segundos, entonces f (200, 500) ya está en 31 segundos. Es curioso que al medir el tiempo de ejecución usando% timeit, el resultado sea mucho menos que real. Obviamente, la primera ejecución de la función lleva la mayor parte del tiempo, mientras que el resto simplemente usa los resultados de su memorización. Mentiras, mentiras descaradas y estadísticas.
La recursión no es necesaria, miramos más allá
Entonces, en las pruebas, por ejemplo, aparece f (9477, 10000), pero mi patética f (200, 500) ya no se ajusta en el momento adecuado. Entonces hay otra solución, sin recurrencia, continuaremos su búsqueda. Complementé el código contando las llamadas de función con ciertos parámetros para ver en qué se descompuso finalmente. Para 10 intentos, se obtuvieron los siguientes resultados:
f (3.10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2 , 5) + 1 * f (2,4) + 1 * f (2,3) + 1 * f (3,3)
f (4.10) = 27+ 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2 , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5.10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2 , 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3 , 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7,10) = 55+ 1 * f (2,5) + 5 * f (2,4) + 15 * f (2,3) + 15 * f (3,3) + 10 * f (4 , 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8,10) = 27+ 1 * f (2,4) + 6 * f (2,3) + 6 * f (3,3) + 5 * f (4,4) + 4 * f (5 , 5) + 3 * f (6.6) + 2 * f (7.7) + 1 * f (8.8)
f (9,10) = 7+ 1 * f (2,3) + 1 * f (3,3) + 1 * f (4,4) + 1 * f (5,5) + 1 * f (6 , 6) + 1 * f (7.7) + 1 * f (8.8) + 1 * f (9.9)
Alguna regularidad es visible:

Estos coeficientes se calculan teóricamente. Cada azul es la suma de la parte superior e izquierda. Y los violetas son los mismos azules, solo en el orden inverso. Puede calcular, pero esto es nuevamente una recursión, y en eso me decepcionó. Lo más probable es que muchos (es una pena que no sea yo) ya hayan aprendido estos números, pero por ahora mantendré la intriga, siguiendo mi propia solución. Decidí escupirles e ir al otro lado.
Abrió el exel, construyó una placa con los resultados de la función y comenzó a buscar patrones. C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), donde $ 2 es la fila con el número de huevos (1-13), $ B es la columna con el número de intentos (1-20), C3 - celda en la intersección de dos huevos y un intento.
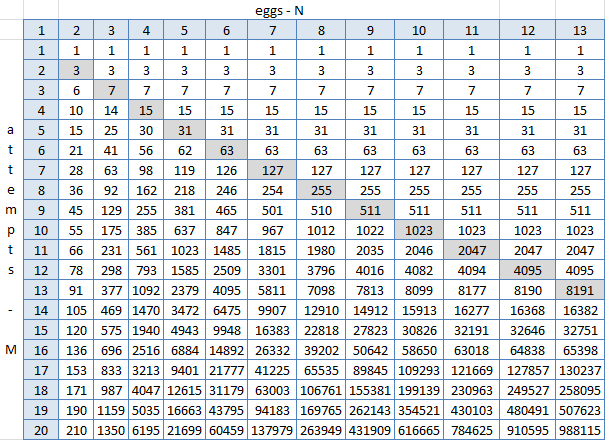
La diagonal gris es N = M, y aquí es claramente visible que a su derecha (para N> M) nada cambia. Se puede ver, pero no puede ser de otra manera, porque estos son todos los resultados del trabajo de la fórmula, en la que se da por hecho que cada celda es igual a la suma de la parte superior, superior izquierda y una. Pero no se encontró alguna fórmula universal donde pueda sustituir N y M y obtener el número de piso. Spoiler: no existe. Pero entonces, es tan simple crear esta tabla en Excel, ¿tal vez es posible generar la misma python y arrastrar las respuestas?
Numpy no lo haces
Recuerdo que hay NumPy, que está diseñado para funcionar con matrices multidimensionales, ¿por qué no probarlo? Para comenzar, necesitamos una matriz unidimensional de ceros de tamaño N + 1 y una matriz unidimensional de unidades de tamaño N. Tome la primera matriz de cero al penúltimo elemento, agréguela de manera elemento con la primera matriz desde el primer elemento hasta el último y con una matriz de unidades. A la matriz resultante, agregue cero al principio. Repite M veces. El número de elemento N de la matriz resultante será la respuesta. Los primeros 3 pasos se ven así:
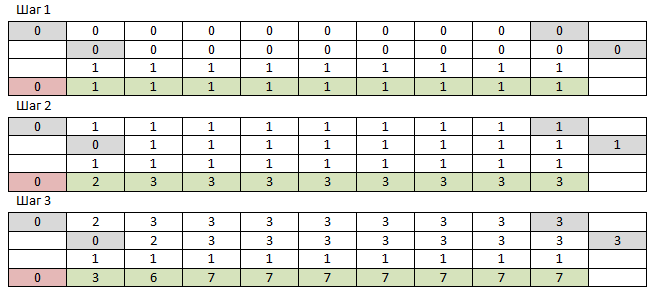
NumPy funciona tan rápido que no guardé toda la tabla, cada vez que leo la fila necesaria nuevamente. Una cosa: el resultado de trabajar en grandes cantidades fue incorrecto. Los rangos más altos son como esos, mientras que los más bajos no lo son. Así es como se ven los errores aritméticos de los números de punto flotante acumulados de múltiples adiciones. No importa: puede cambiar el tipo de matriz a int. No, problema: resultó que, en aras de la velocidad, NumPy solo funciona con sus tipos de datos, y su int, a diferencia del Python int, no puede ser más de 2 ^ 64-1, después de lo cual se desborda silenciosamente y continúa con -2 ^ 64. Y en realidad espero números de menos de tres mil caracteres. Pero funciona muy rápido, f (9477, 10000) ejecuta 233 ms, simplemente resulta una especie de tontería en la salida. Ni siquiera daré el código, ya que tal cosa. Trataré de hacer lo mismo una pitón limpia.
Iterado, iterado, pero no iterado
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]
44 segundos para calcular f (9477, 10000) es un poco demasiado. Pero absolutamente seguro. ¿Qué se puede optimizar? Primero, no hay necesidad de considerar todo a la derecha de la diagonal M, M. El segundo: considerar la última matriz como un todo, por el bien de una celda. Para esto, se ajustarán las dos últimas dos celdas de la anterior. Para calcular f (10, 20), solo estas celdas grises serán suficientes:
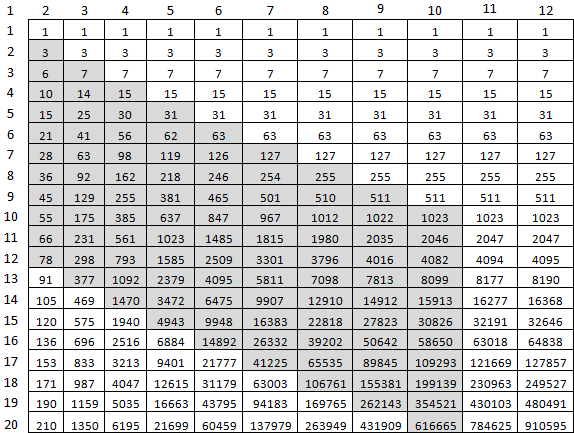
Y así se ve en el código:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn:
Y que piensas f (9477, 10000) en 2 segundos! Pero esta entrada es demasiado buena, la longitud de la matriz en cualquier etapa no será más de 533 elementos (10000-9477). Veamos f (5477, 10000) - 11 segundos. También es bueno, pero solo en comparación con 44 segundos: veinte pruebas con este tiempo no pasarán.
No es eso Pero como hay una tarea, entonces hay una solución, la búsqueda continúa. Empecé a mirar la tabla de Excel nuevamente. La celda a la izquierda de (m, m) es siempre una menos. Y la celda a la izquierda ya no está allí, en cada fila la diferencia se hace más grande. La celda de abajo (m, m) siempre es el doble de grande. Y la celda debajo de ella ya no es dos veces, sino un poco más pequeña, pero para cada columna de manera diferente, cuanto más lejos, más grande. Y también los números en una línea al principio crecen rápidamente, y luego al medio lentamente. Permítanme construir una tabla de diferencias entre las celdas vecinas, ¿qué patrón aparecerá allí?
Calentador
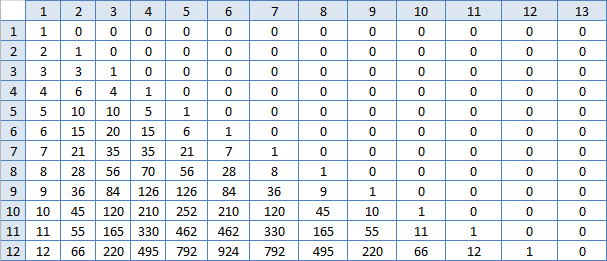
Bah, números familiares! Es decir, la suma N de estos números en la línea número M ¿es esta la respuesta? Es cierto que contarlos es casi lo mismo que ya hice, es poco probable que esto acelere en gran medida el trabajo. Pero tienes que probar:
f (9477, 10000): 17 segundos def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])
O 8, si cuentas solo la mitad del triángulo def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2:
No quiere decir que sea una solución más óptima. Funciona más rápido en algunos datos, más lento en algunos. Debemos ir más profundo. ¿Qué es este triángulo con números que aparecieron en la solución dos veces? Es una pena admitirlo, pero he olvidado con seguridad las matemáticas superiores, donde el triángulo debe haber figurado, así que tuve que buscarlo en Google.
Bingo!
Triángulo de Pascal , como se le llama oficialmente. Tabla de coeficientes binomiales infinitos. Entonces, la respuesta al problema con N huevos y M arroja es la suma de los primeros coeficientes N en la expansión del binomio de Newton del grado M, excepto cero.
Se puede calcular un coeficiente binomial arbitrario a través de los factores del número de fila y el número de coeficiente en la fila: bk = m! / (N! * (Mn!)). Pero la mejor parte es que puede calcular secuencialmente los números en la cadena, conociendo su número y coeficiente cero (siempre uno): bk [n] = bk [n-1] * (m - n + 1) / n. En cada paso, el numerador disminuye en uno y el denominador aumenta. Y la solución final concisa se ve así:
def height(n, m): h, bk = 0, 1
33 ms para el cálculo de f (9477, 10000)! Esta solución también se puede optimizar, aunque en los rangos dados y funciona bien. Si n se encuentra en la segunda mitad del triángulo, entonces podemos invertirlo en mn, calcular la suma de los primeros coeficientes n y restarlo de 2 ^ m-2. Si n está cerca del medio ym es impar, entonces los cálculos también se pueden reducir: la suma de la primera mitad de la línea será 2 ^ (m-1) -1, el último coeficiente en la primera mitad se puede calcular mediante factoriales, su número es (m-1) / 2, y luego continuar sumando coeficientes si n está en la mitad derecha del triángulo, o restar si está en la izquierda. Si m es par, entonces ni siquiera puede contar la mitad de la línea, pero puede encontrar la suma de los primeros coeficientes m / 2 + 1 calculando el promedio a través de factoriales y sumando la mitad a 2 ^ (m-1) -1. En los datos de entrada en la región de 10 ^ 6, esto reduce notablemente el tiempo de ejecución.
Después de una decisión exitosa, comencé a buscar la investigación de otra persona sobre este tema, pero encontré lo mismo, de las entrevistas, con solo dos huevos, y esto no es deporte. Decidí que Internet estará incompleto sin mi decisión, y aquí está.