Julia Conocido

Oda a Julia

Es muy difícil transmitir todo el entusiasmo que acompañó el lanzamiento de los primeros programas y la corrección de los primeros errores con este lenguaje. Simple y hermoso como Python , un poco como Fortran , trabajo conveniente con matrices y gráficos, así como la capacidad de realizar una feroz optimización y paralelización incluso para tontos como yo mis compañeros de clase Puede trabajar en diferentes niveles de abstracción: desde la programación de alto nivel con tipeo dinámico, puede pasar a los comandos de ensamblador, es decir, aquí tiene tanto la accesibilidad de Python como la velocidad de ejecución de los contadores de Fortran. No puedo deshacerme de la sensación de que Mathcad , Scilab e incluso, Dios me perdone, C ++ están comenzando a desvanecerse en mi corazón.

Aprendí sobre el idioma tropezando accidentalmente con una publicación de Khabrovian y, como un estudiante impresionable debería, comencé a buscar orientación, preferiblemente en ruso. Dado que el lenguaje ha evolucionado constantemente durante seis años, las fuentes de información ya escasas se volvieron obsoletas y la emoción comenzó a disminuir. Pero con el comienzo de un nuevo curso de laboratorio sobre modelado de fenómenos físicos con la libre elección de un lenguaje de programación, todavía había una motivación para comenzar a conocer a Julia. Además, en agosto, el lenguaje "suma 1.0" .

El material presentado a continuación fue planeado como una introducción al lenguaje en el que se escribieron todos los documentos de laboratorio y se recopiló un manual de capacitación.

Julia es un lenguaje de programación de escritura dinámica de alto nivel y alto rendimiento para cálculos matemáticos. La sintaxis es similar a la familia matlab, el lenguaje está escrito en C , C ++ y Scheme , es posible llamar a las bibliotecas Sysh

Instalación

Bueno, todo finalmente se calmó, ahora a nuestra disposición:

• Símbolo del sistema JuliaPRO : todas las habilidades de Yulina directamente del intérprete.
• Juno es un hermoso IDE con una ventana para gráficos y un espacio de trabajo donde puede ver el contenido de todos los objetos.
• Jupyter : inicia el núcleo informático en la consola y puede ejecutar código directamente en el navegador. (Además de Julia, Python también está presente)

Veamos qué puede hacer esta calculadora ... Soporte Unicode: puede usar el alfabeto cirílico, los jeroglíficos y llamar a pi la letra griega. Y no puede especificar explícitamente la multiplicación entre el número y la variable (en ese orden y sin un espacio):

x = 5+8 2x - 3x + 2x^2 Out: 325 

Todos los signos necesarios también están en su lugar: + =, * =, >> =, etc. (Firme ">>" (desplazamiento de bits a la derecha). Signos de comparación:>,> =, <, <=, == ,! =. Las desigualdades se pueden combinar en cadenas:

 y = 5 y += 2 4 <= y < 8 Out: true 

Números complejos disponibles:

 (2-1im)*(4+3im) Out: 11 + 2im 

Y funciones para trabajar con ellos:

• real (z) es la parte real,
• imag (z) es la parte imaginaria,
• conj (z) es el conjugado complejo,
• abs (z) - módulo,
• abs2 (z) es el cuadrado del módulo,
• ángulo (z) es el argumento de un número complejo.

Puede usar números racionales usando "//" y las funciones correspondientes:

• num (x) - numerador,
• den (x) - denominador,
• float (x) - convierte a decimal

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

Julia tiene la capacidad de controlar la representación interna de datos:

• typeof (obj) - tipo de objeto
• typemax (obj) es el número máximo de este tipo
• typemin (obj) - mínimo
• eps () - máquina cero
• BigInt es un gran todo
• BigFloat - gran punto flotante

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

Las funciones

Kit de funciones

• abs (x) es el módulo de un número,
• abs2 (x) es el cuadrado del módulo,
• sqrt (x) es la raíz cuadrada,
• cbrt (x) es la raíz cúbica,
• exp (x) es el exponente del número,
• log (x) es el logaritmo natural,
• log10 (x) - logaritmo decimal,
• log (b, x) es el logaritmo de x en la base b.
  Además de trigonométrico, hiperbólico, Airy, Bessel y muchos otros.

Funciones personalizadas

 function () #  end 

La función devuelve el resultado de la última expresión (usuario de Mathcad con hipo).

 function cube(x) x^3 end cube(4) Out: 64 

Bueno, o indicamos explícitamente:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

Los valores devueltos se pueden recopilar en una tupla:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

Las funciones pueden tomar tuplas, valores predeterminados, palabras clave. Si no hay corchetes después del nombre de la función, se considera como una variable y puede asignarse a otra variable o transferirse a la función como un parámetro. Julia también admite un estilo funcional de programas de escritura (hola Lisp)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

Matrices

Como usuario de Scilab , ni siquiera noté la sustitución: puede especificar una matriz usando la función:

• Array {T} (undef, dims ...): una matriz de dims de tipo T y dimensión
• ceros (T, dims ...) - Matriz de ceros
• unos (T, dims ...) - o unidades
  La indexación comienza con uno , en lugar de $ - end , y se definen todas las operaciones necesarias para las matrices (para realizar, por ejemplo, la suma o multiplicación por elementos, debe colocar un punto delante del operador).

(Ahora está claro cómo insertar imágenes, pero está bien ...)

Funciones básicas:

• det (A) - calcular determinante
• A ' - transponer la matriz
• inv (A) - matriz invertida
• longitud (A) - número de elementos
• ndims (A) - número de dimensiones
• tamaño (A) - tupla de dimensiones
• tamaño (A, n) - dimensión en una dirección dada
• copy (A) : crea una copia de la matriz
• linspace (inicio, final, paso) o
  linspace (inicio: paso: fin) : crea una matriz unidimensional

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

Puede seleccionar partes de la matriz especificando un rango de índices a lo largo de la dimensión con el signo ":".

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

Aquí usamos rand (), que devuelve una matriz de números aleatorios de una dimensión dada, y reshape (), que cambia la dimensión de la matriz a la especificada.

 for a in A #   a   A end 

o

 for i in eachindex(A) #     i end 

o

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

Gráficos

Para usar gráficos, debe descargar un paquete del repositorio para elegir:

• Pkg.add ("Parcelas")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("Winston")

De estos, el más popular es Pythonic PyPlot . Los módulos se conectan mediante el comando, por ejemplo:

 using PyPlot 

Sin embargo, intentemos Gaston usando Gnuplot (swing por separado).
Cargado por el equipo de Gaston.jl

  Pkg.add("Gaston") 

Y directo al grano:

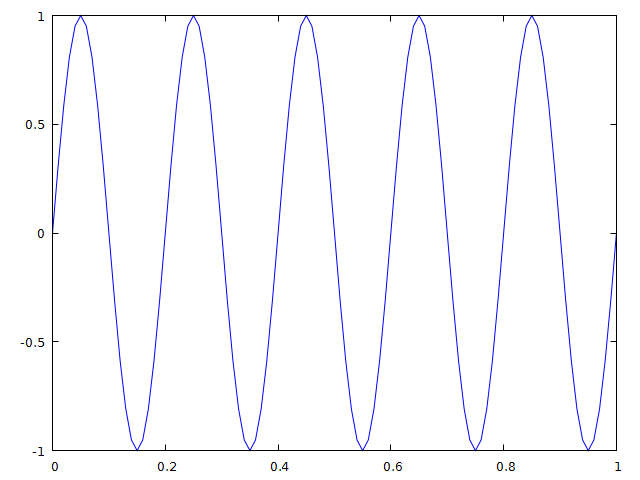
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

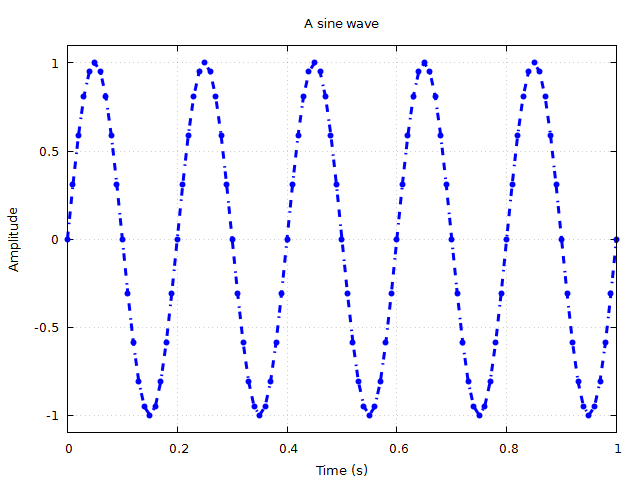
 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

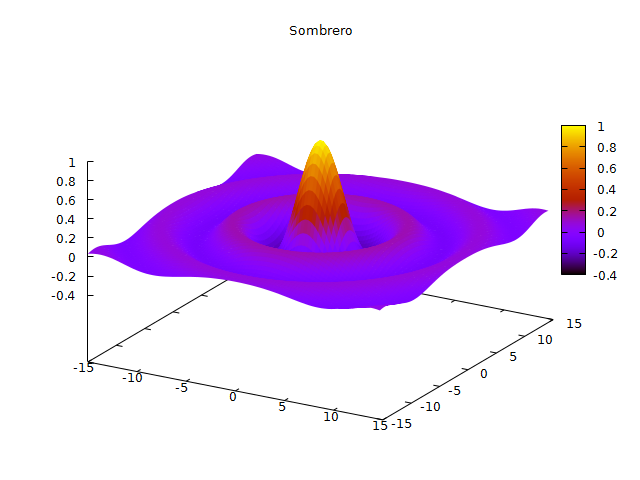
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

Puede crear múltiples ventanas gráficas (no funciona en Jupyter ) usando el comando h = figure () (solo inserte entre parcelas). Para guardar el gráfico como un archivo de imagen, use los comandos
set_filename ("name.png") # si no se especifica, se mostrará
printfigure ("png") # guardar en archivo, PNG, PDF, SVG y GIF disponibles
Más información del paquete de Gaston

Conclusión

Hay muchos más paquetes gráficos para todos los gustos y que cubren casi todas las necesidades. Además, los paquetes auxiliares se están desarrollando con might y main. Aquí tiene computación cuántica y bioinformática, y aprendizaje automático, y muchos más problemas apremiantes como diferencias y derivados .

En general, Julia es hermosa, inteligente y muy prometedora, y es extremadamente inadmisible dejarla sin la debida atención.