Este artículo analiza las similitudes y diferencias entre los dos enfoques para resolver problemas algorítmicos:
programación dinámica (programación dinámica) y el principio de
"divide y vencerás" (divide y vencerás). Compararemos utilizando dos algoritmos como ejemplo:
búsqueda binaria (cómo encontrar rápidamente un número en una matriz ordenada) y
distancia de Levenshtein (cómo convertir una fila a otra con un número mínimo de operaciones).
Quiero señalar de inmediato que esta comparación y explicación no pretende ser extremadamente correcta. Y tal vez incluso algunos profesores universitarios quisieran expulsarme :) Este artículo es solo mi intento personal de resolver las cosas y comprender qué es la programación dinámica y cómo está involucrado el principio de "divide y vencerás".Entonces, comencemos ...
El problema
Cuando
comencé a estudiar algoritmos, fue difícil
para mí entender la idea básica de la programación dinámica (en adelante
DP , de Dynamic Programming) y cómo difiere del enfoque de "divide y vencerás" (más
DC , de divide y vencerás). Cuando se trata de comparar estos dos paradigmas, generalmente
muchos usan con éxito la función de Fibonacci para ilustrar. Y esta es una gran ilustración. Pero me parece que cuando usamos
la misma tarea para ilustrar DP y DC, perdemos un detalle importante que puede ayudarnos a detectar la diferencia entre los dos enfoques más rápido. Y este detalle es que estas dos técnicas se manifiestan mejor para resolver
diferentes tipos de problemas.
Todavía estoy en el proceso de aprender DP y DC y no puedo decir que entendí completamente estos conceptos. Pero todavía espero que este artículo arroje luz adicional y ayude a dar el siguiente paso en el estudio de enfoques tan importantes como la programación dinámica y la división y conquista.
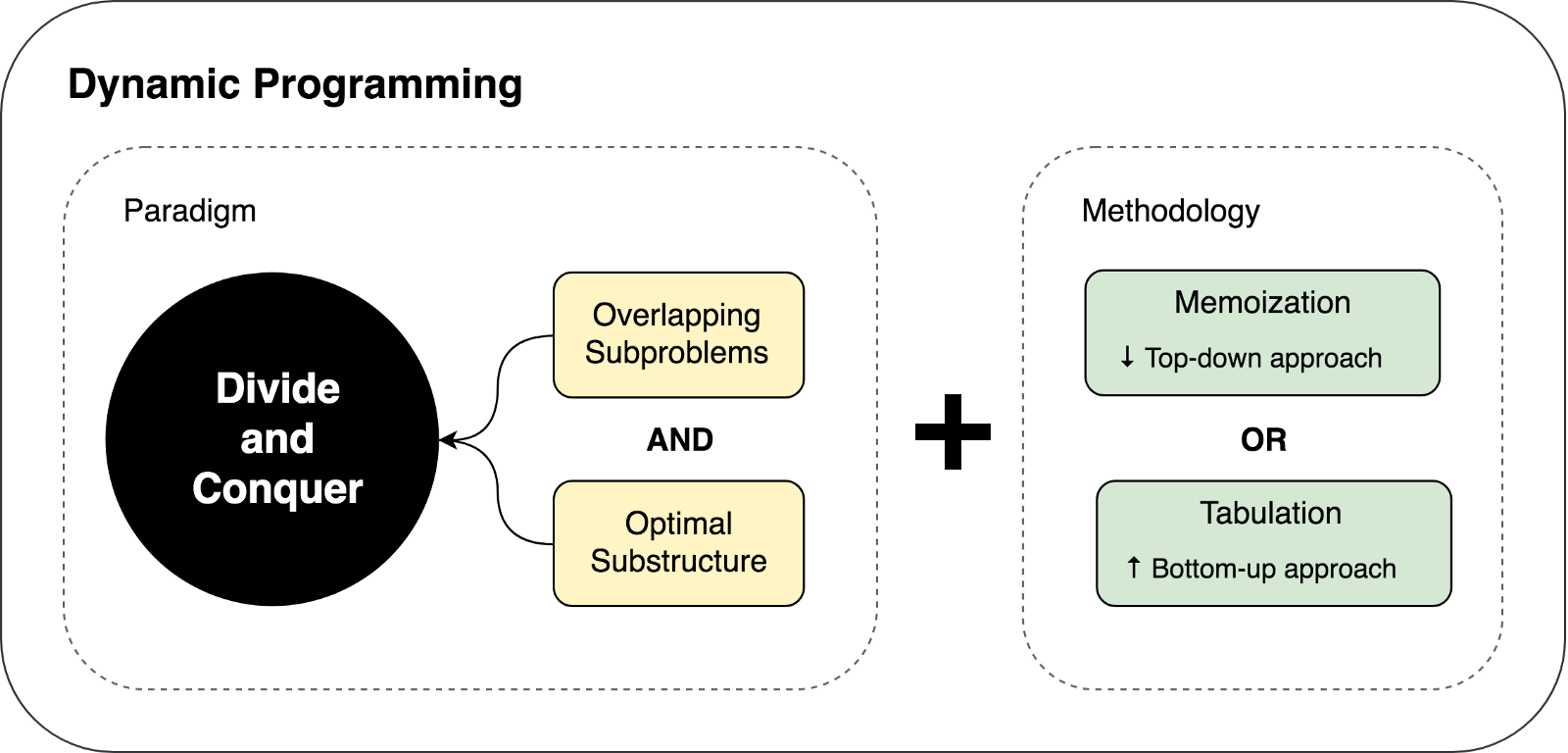
Similitudes entre DP y DC
Por la forma en que veo estos dos conceptos ahora, puedo concluir que
DP es una versión extendida de DC .
No los consideraría algo completamente diferente. Debido a que estos dos conceptos
dividen recursivamente un problema en dos o más subproblemas del mismo tipo hasta que estos subproblemas sean lo suficientemente fáciles de resolver directamente. Además, todas las soluciones al subproblema se combinan para dar una respuesta al problema original original.
Entonces, ¿por qué entonces todavía tenemos dos enfoques diferentes (DP y DC) y por qué llamé a la programación dinámica una extensión? Esto se debe a que la programación dinámica se puede aplicar a tareas que tienen ciertas
características y limitaciones . Y solo en este caso DP expande DC mediante dos técnicas:
memorización y
tabulación .
Vamos a profundizar un poco más en los detalles ...
Limitaciones y características necesarias para la programación dinámica.
Como acabamos de descubrir, hay dos características clave que debe tener una tarea / problema para que podamos tratar de resolverlo utilizando la programación dinámica:
- Subestructura óptima : debería ser posible componer una solución óptima a un problema desde una solución óptima a sus subtareas.
- Subproblemas de intersección : el problema debe desglosarse en subproblemas, que a su vez se reutilizan repetidamente. En otras palabras, un enfoque recursivo para resolver el problema implicaría una solución múltiple ( no una sola) para el mismo subproblema, en lugar de producir subproblemas nuevos y únicos en cada ciclo recursivo.
Tan pronto como podamos encontrar estas dos características en el problema que estamos considerando, podemos decir que se puede resolver mediante programación dinámica.
Programación dinámica como una extensión del principio de "divide y vencerás"
DP extiende DC con la ayuda de dos técnicas (
memorización y
tabulación ), cuyo propósito es guardar soluciones a subproblemas para su futura reutilización. Por lo tanto, las soluciones se almacenan en caché por subproblema, lo que conduce a una mejora significativa en el rendimiento del algoritmo. Por ejemplo, la complejidad temporal de una implementación recursiva “ingenua” de la función Fibonacci es
O(2 n ) . Al mismo tiempo, una solución basada en programación dinámica se ejecuta en solo
(n) .
La memorización (llenar el caché de arriba a abajo) es una técnica de almacenamiento en caché que utiliza soluciones recién calculadas para subtareas. La función de Fibonacci que usa la técnica de memorización se vería así:
memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] }
La tabulación (llenar el caché de abajo hacia arriba) es una técnica similar, pero que se centra principalmente en llenar el caché y no en encontrar una solución al subproblema. El cálculo de los valores que deben almacenarse en caché es más fácil en este caso para realizarse de forma iterativa, en lugar de recurrente. La función de Fibonacci que usa la técnica de tabulación se vería así:
tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] }
Puede leer más sobre la comparación de la memorización y la tabulación
aquí .
La idea principal que debe captarse en estos ejemplos es que, dado que nuestros problemas de DC tienen subproblemas superpuestos, podemos usar el almacenamiento en caché de soluciones a subproblemas utilizando una de dos técnicas de almacenamiento en caché: memorización y tabulación.
Entonces, ¿cuál es la diferencia entre DP y DC al final
Aprendimos sobre las limitaciones y requisitos previos para usar la programación dinámica, así como las técnicas de almacenamiento en caché utilizadas en el enfoque DP. Tratemos de resumir y representar los pensamientos anteriores en la siguiente ilustración:
Intentemos resolver un par de problemas utilizando DP y DC para demostrar ambos enfoques en acción.
Divide y vencerás Ejemplo: Búsqueda binaria
El algoritmo de búsqueda
binaria es un algoritmo de búsqueda que encuentra la posición del elemento solicitado en una matriz ordenada. En la búsqueda binaria, comparamos el valor de la variable con el valor del elemento en el medio de la matriz. Si no son iguales, entonces la mitad de la matriz en la que el elemento deseado no puede excluirse de una búsqueda adicional. La búsqueda continúa en esa mitad de la matriz, en la que se puede ubicar la variable deseada hasta que se encuentre. Si la siguiente mitad de la matriz no contiene elementos, la búsqueda se considera completa y concluimos que la matriz no contiene el valor deseado.
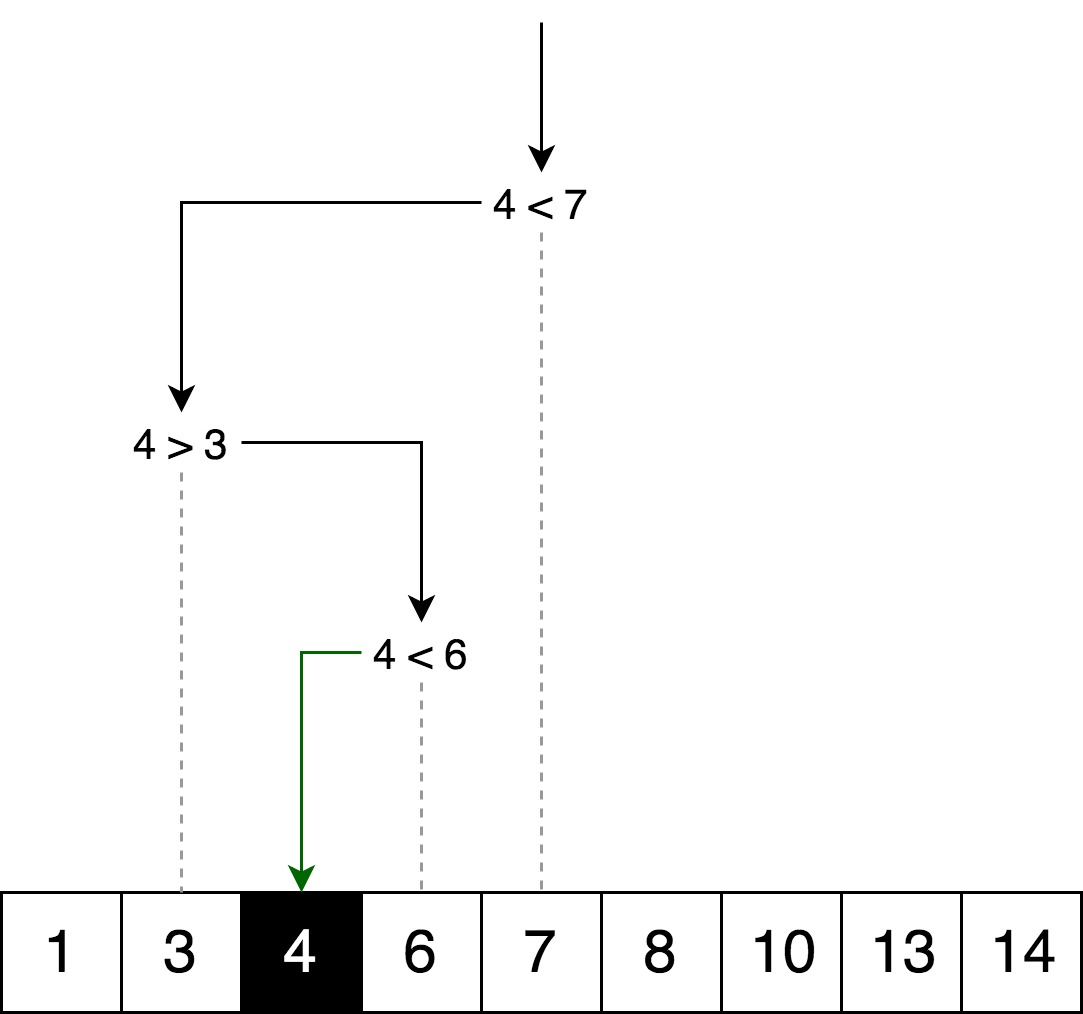
EjemploLa siguiente ilustración es un ejemplo de una búsqueda binaria para el número 4 en una matriz.
Representemos la misma lógica de búsqueda, pero en forma de un "árbol de decisión".
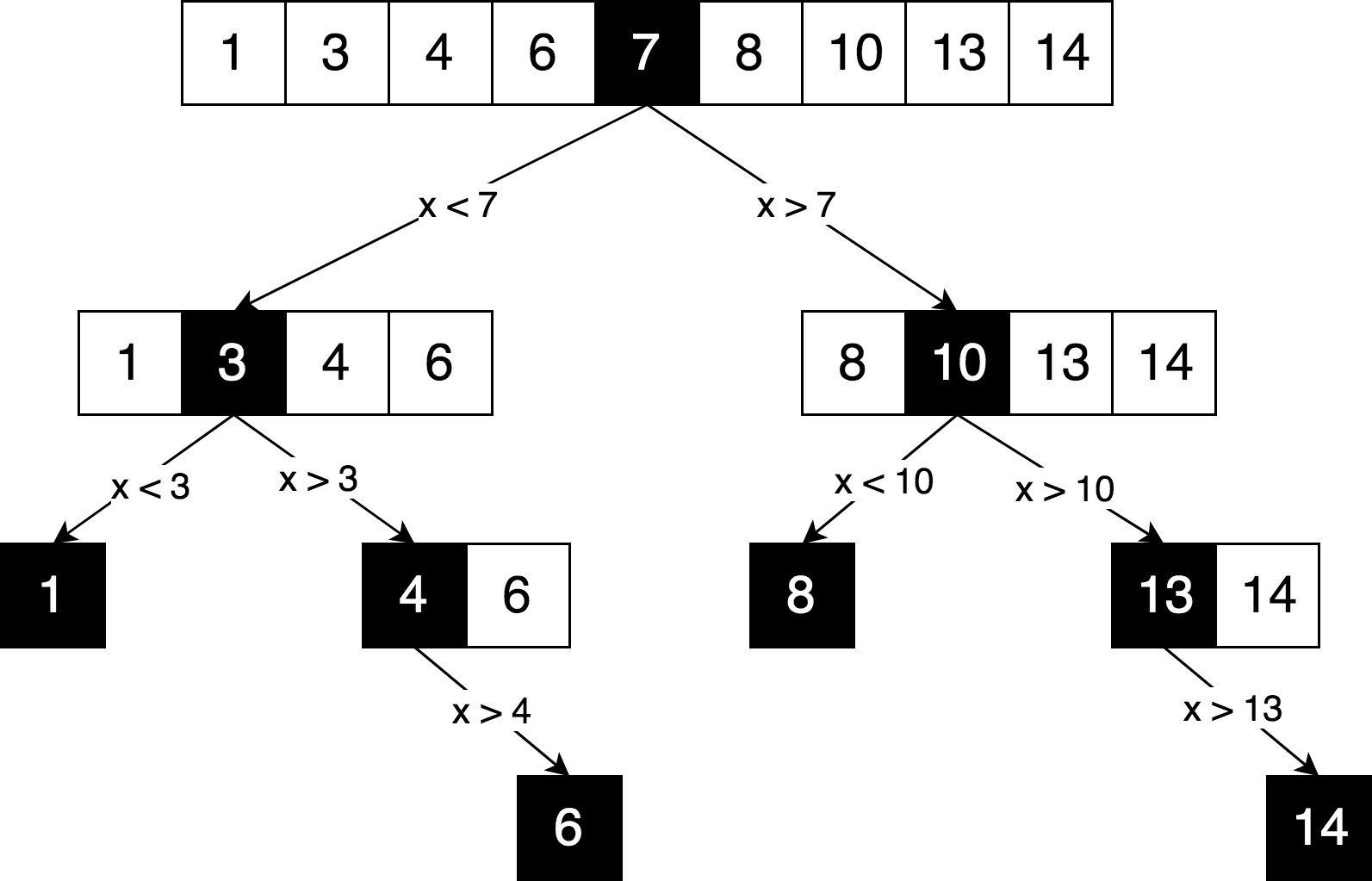
Puede ver en este diagrama un principio claro de "divide y vencerás", utilizado para resolver este problema. Dividimos iterativamente nuestra matriz original en submatrices e intentamos encontrar el elemento que estamos buscando en ellas.
¿Podemos resolver este problema usando programación dinámica?
No Por la razón de que esta tarea
no contiene subproblemas de intersección . Cada vez que dividimos una matriz en partes, ambas partes son completamente independientes y no se superponen. Y de acuerdo con los supuestos y las limitaciones de la programación dinámica que discutimos anteriormente, los subproblemas deben superponerse de alguna manera,
deben ser repetitivos .
Por lo general, cada vez que un árbol de decisión se ve exactamente como un
árbol (y
no como un gráfico ), lo más probable es que no haya subproblemas superpuestos,
Implementación de algoritmoAquí puede encontrar el código fuente completo del algoritmo de búsqueda binaria con pruebas y explicaciones.
function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);
Ejemplo de programación dinámica: distancia de edición
Por lo general, cuando se trata de explicar la programación dinámica,
la función de Fibonacci se usa como ejemplo. Pero en nuestro caso, tomemos un ejemplo un poco más complejo. Cuantos más ejemplos, más fácil es entender el concepto.
La distancia de edición (o la distancia de Levenshtein) entre dos líneas es el número mínimo de operaciones para insertar un carácter, eliminar un carácter y reemplazar un carácter con otro, necesario para convertir una línea en otra.
EjemploPor ejemplo, la distancia de edición entre las palabras "gatito" y "sentado" es 3, porque necesita realizar tres operaciones de edición (dos reemplazos y una inserción) para convertir una línea en otra. Y es imposible encontrar una opción de conversión más rápida con menos operaciones:
- gatito → sitten (reemplazando "k" con "s")
- sitten → sittin (reemplazando "e" con "i")
- sittin → sentado (inserte "g" completamente).
Aplicación de algoritmoEl algoritmo tiene una amplia gama de aplicaciones, por ejemplo, para corrección ortográfica, sistemas de corrección de reconocimiento óptico, búsqueda de cadenas inexacta, etc.
Definición matemática de un problema.Matemáticamente, la distancia de Levenstein entre dos líneas
a, b (con longitudes | a | y
|b| respectivamente) está determinada por la función de
function lev(|a|, |b|) , donde:
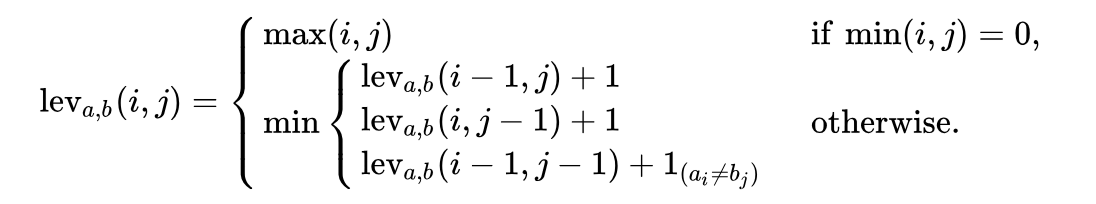
Tenga en cuenta que la primera línea en la función
min corresponde a la operación de
eliminación , la segunda línea corresponde a la operación de
inserción y la tercera línea corresponde a la operación de
reemplazo (en caso de que las letras no sean iguales).
ExplicaciónTratemos de descubrir qué nos dice esta fórmula. Tome un ejemplo simple de encontrar la distancia mínima de edición entre las líneas
ME y
MY . Intuitivamente, ya sabe que la distancia mínima de edición es una (
1 ) operación de reemplazo (reemplace "E" con "Y"). Pero formalicemos nuestra solución y conviértala en una forma algorítmica, para poder resolver versiones más complejas de este problema, como transformar la palabra
sábado en
domingo .
Para aplicar la fórmula a la transformación ME → MY, primero debemos encontrar la distancia mínima de edición entre ME → M, M → MY y M → M. A continuación, debemos elegir el mínimo de tres distancias y agregarle una operación (+1) de la transformación E → Y.
Entonces, ya podemos ver la naturaleza recursiva de esta solución: la distancia de edición mínima ME → MY se calcula en función de las tres transformaciones posibles anteriores. Por lo tanto, ya podemos decir que este es un algoritmo de divide y vencerás.
Para explicar más el algoritmo, pongamos nuestras dos filas en una matriz:
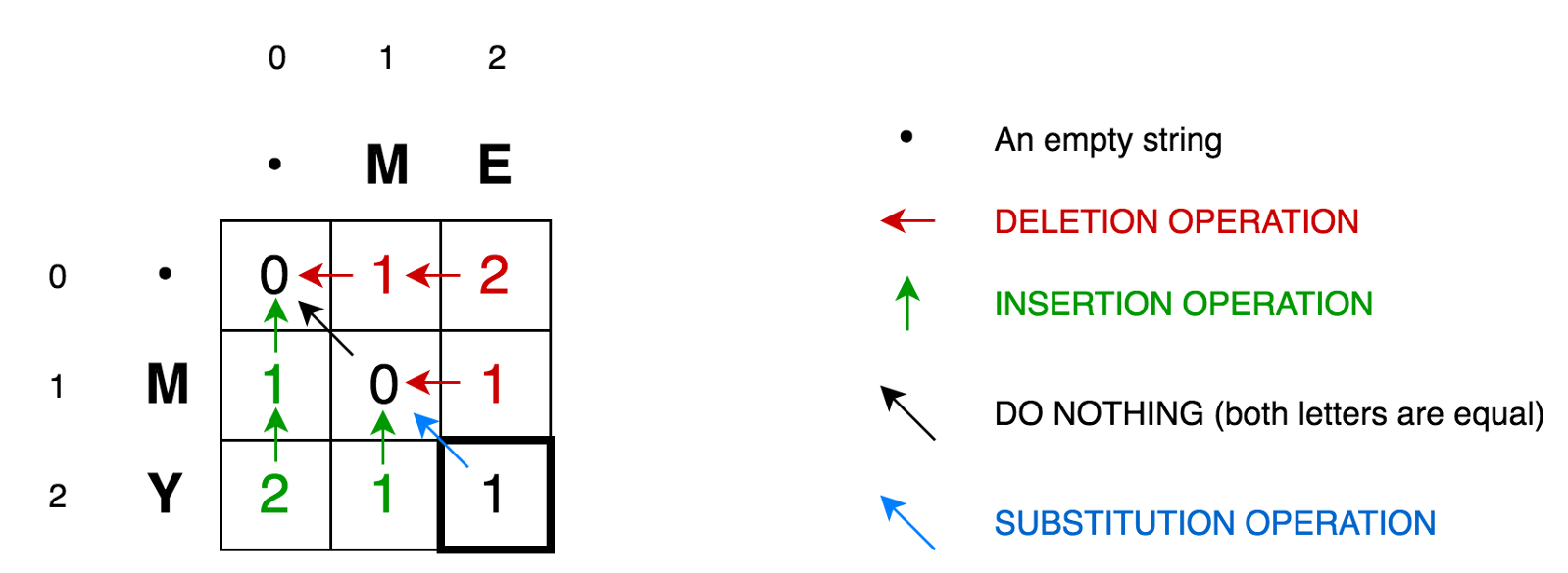La celda (0,1) contiene el número rojo 1. Esto significa que debemos realizar 1 operación para convertir M en una cadena vacía: eliminar M. Por lo tanto, hemos marcado este número en rojo.
La celda (0,2) contiene un número rojo 2. Esto significa que necesitamos realizar 2 operaciones para transformar la cadena ME en una cadena vacía: eliminar E, eliminar M.
La celda (1,0) contiene un número verde 1. Esto significa que necesitamos 1 operación para transformar una cadena vacía en M - pegar M. Marcamos la operación de inserción en verde.
La celda (2,0) contiene un número verde 2. Esto significa que necesitamos realizar 2 operaciones para convertir una cadena vacía en una cadena MY - inserte Y, inserte M.
La celda (1,1) contiene el número 0. Esto significa que no necesitamos realizar ninguna operación para convertir la cadena M a M.
La celda (1,2) contiene el número rojo 1. Esto significa que debemos realizar 1 operación para transformar la cadena ME en M - eliminar E.
Y así sucesivamente ...
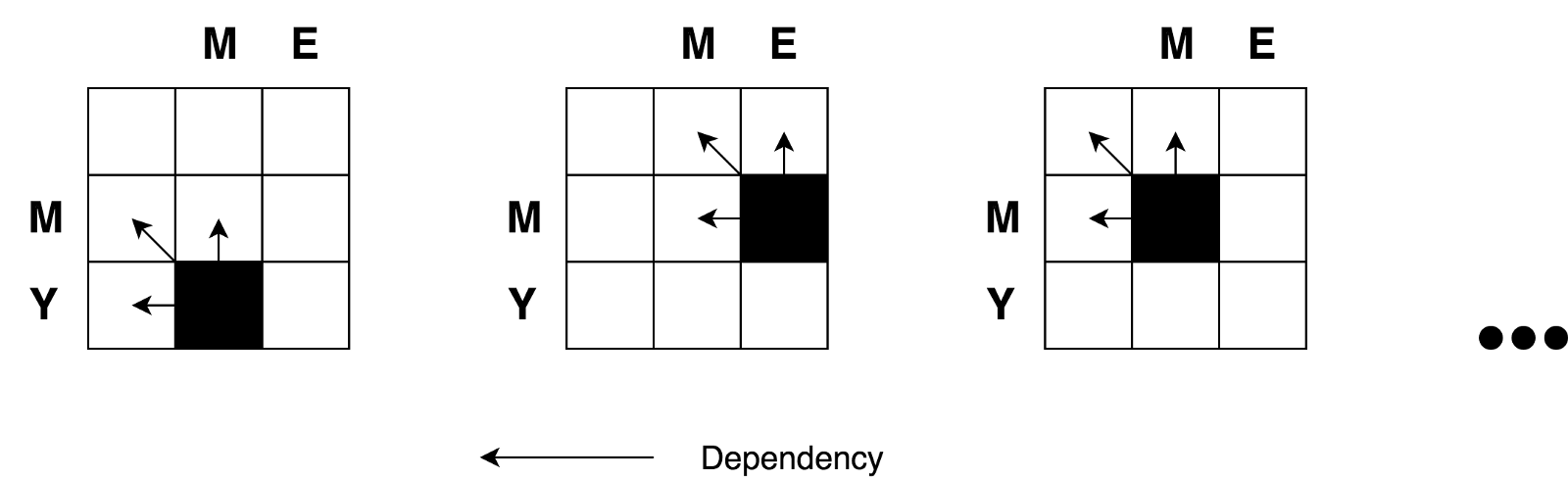
No parece difícil para matrices pequeñas, como la nuestra (solo 3x3). Pero, ¿cómo podemos calcular los valores de todas las celdas para matrices grandes (por ejemplo, para una matriz de 9x7 en la transformación sábado → domingo)?
La buena noticia es que, de acuerdo con la fórmula, todo lo que necesitamos para calcular el valor de cualquier celda con coordenadas
(i,j) son solo los valores de 3 celdas vecinas
(i-1,j) ,
(i-1,j-1) y
(i,j-1) . Todo lo que tenemos que hacer es encontrar el valor mínimo de tres celdas vecinas y agregar una (+1) a este valor si tenemos letras diferentes en la i-ésima fila y la j-ésima columna.
De nuevo, puede ver claramente la naturaleza recursiva de esta tarea.
También vimos que estábamos lidiando con una tarea de dividir y conquistar. Pero, ¿podemos aplicar programación dinámica para resolver este problema? ¿Esta tarea satisface las condiciones de "
problemas de intersección " y "
subestructuras óptimas " mencionadas anteriormente?
Si Construyamos un árbol de decisión.
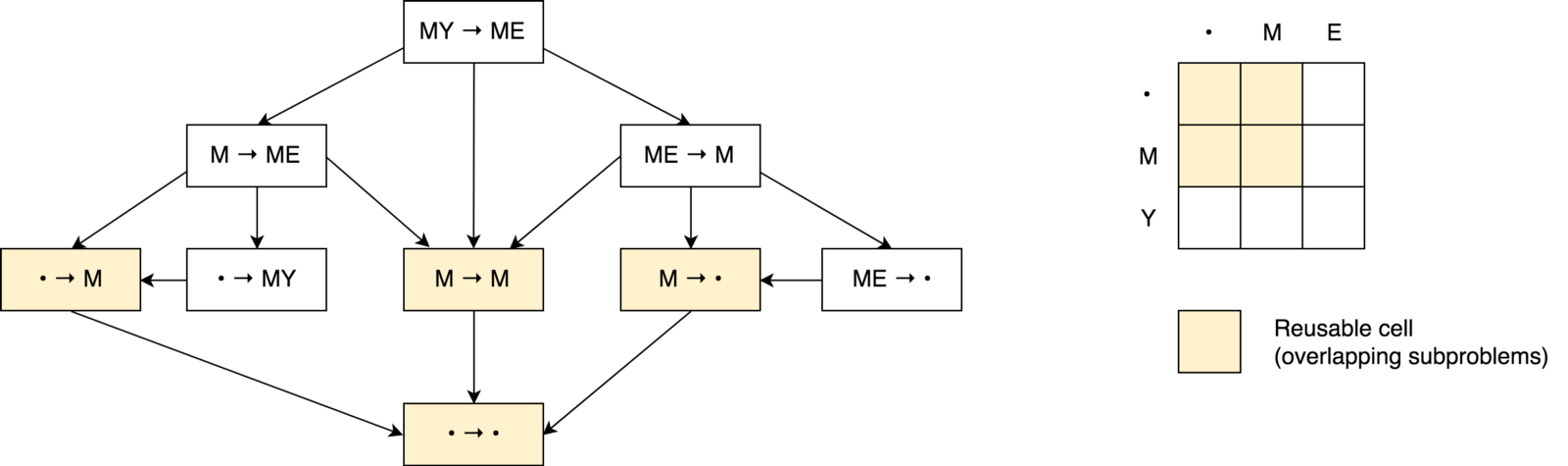
Primero, puede notar que nuestro árbol de decisión se parece más a un
gráfico de decisión que a un
árbol . También puede observar
varias subtareas superpuestas . También se ve que es imposible reducir el número de operaciones y hacerlo más pequeño que el número de operaciones de esas tres celdas vecinas (subproblemas).
También puede observar que el valor en cada celda se calcula en función de los valores anteriores. Por lo tanto, en este caso, se utiliza la técnica de
tabulación (llenando el caché en la dirección ascendente). Verá esto en el ejemplo de código a continuación.
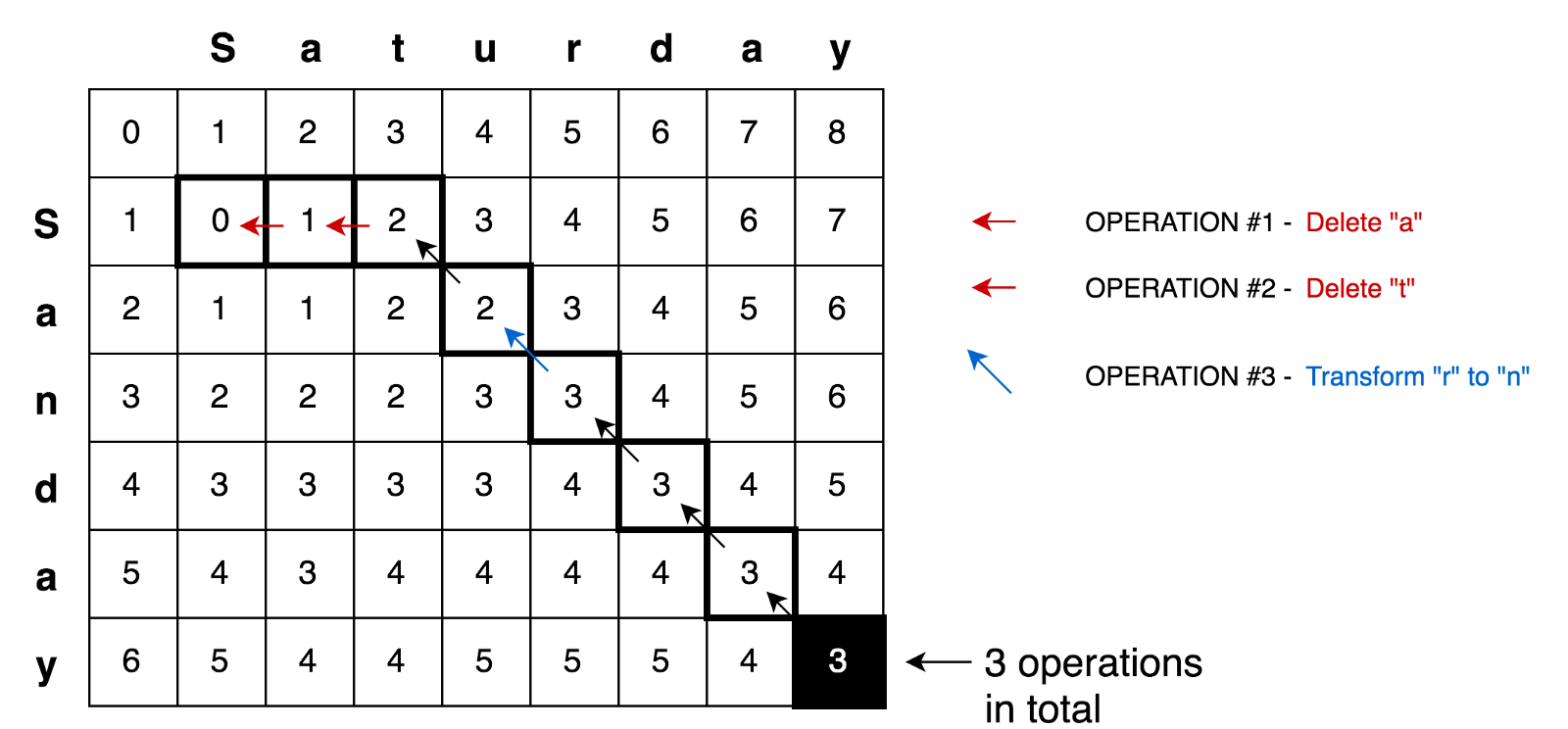
Aplicando todos estos principios, podemos resolver problemas más complejos, por ejemplo, la tarea de transformación Sábado → Domingo:
Ejemplo de códigoAquí puede encontrar una solución completa para encontrar la distancia mínima de edición con pruebas y explicaciones:
function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1,
Conclusiones
En este artículo, comparamos dos enfoques algorítmicos ("programación dinámica" y "divide y vencerás") para resolver problemas. Descubrimos que la programación dinámica utiliza el principio de "divide y vencerás" y puede aplicarse para resolver problemas si el problema contiene subproblemas de intersección y la subestructura óptima (como es el caso con la distancia de Levenshtein). La programación dinámica utiliza además técnicas de memorización y tabulación para preservar las resoluciones secundarias para su posterior reutilización.
Espero que este artículo aclare en lugar de complicar la situación para aquellos de ustedes que han tratado de lidiar con conceptos tan importantes como la programación dinámica y "divide y vencerás" :)
Puede encontrar más ejemplos algorítmicos utilizando programación dinámica, con pruebas y explicaciones en el repositorio de
algoritmos de JavaScript y estructuras de datos .
Codificación exitosa!