“Es fácil. Tomamos la métrica de Schwarzschild, buscamos los símbolos de Christoffel, calculamos su derivada, escribimos la ecuación geodésica, cambiamos algunas coordenadas cartesianas (para no sufrir), obtenemos una gran EDO de varias líneas y la resolvemos. Algo así ".



Ahora está claro que los agujeros negros me chuparon. Son infinitamente fascinantes. La última vez descubrí cómo visualizar la geometría de Schwarzschild. Me tragó el problema de una representación precisa de cómo la curvatura de tal espacio-tiempo afecta la apariencia del cielo (ya que los fotones de fuentes distantes se mueven a lo largo de líneas geodésicas curvadas por un agujero negro) para crear una simulación interactiva. Aquí está el resultado (funciona en el navegador). El truco es maximizar el cálculo de la desviación de los rayos de luz. Todo funciona más o menos normalmente, pero, por supuesto, tal simulación está lejos de ser ideal, porque en realidad no se realiza ningún rastreo allí (para no especialistas: restauración de la ubicación de los rayos de luz que caen en la cámara en el tiempo).

Mi nuevo proyecto corrige esta deficiencia al abandonar la eficiencia / interactividad de la manera más simple: este es un trazador de enrutador puro en la CPU . El rastreo se realiza con la mayor precisión y el mayor tiempo posible. La representación de la imagen de arriba tomó 15 5 minutos (gracias, RK4) en mi computadora portátil.

No hay mejora en comparación con trabajos similares. Realmente disfruto haciéndolo. Estoy escribiendo este artículo para compartir no solo los resultados, como la imagen de arriba ( especialmente porque a otros les fue mejor ), sino también el proceso de creación de estas imágenes , con una discusión / explicación de física e implementación. Idealmente, esto puede inspirar o convertirse en una guía para personas con intereses similares.

Busque nuevas representaciones con la etiqueta sin estrellas en tumlr.

Un poco de óptica pseudo-Riemann

Sombra

Si ya ha probado mi applet , entonces está familiarizado con esta imagen:



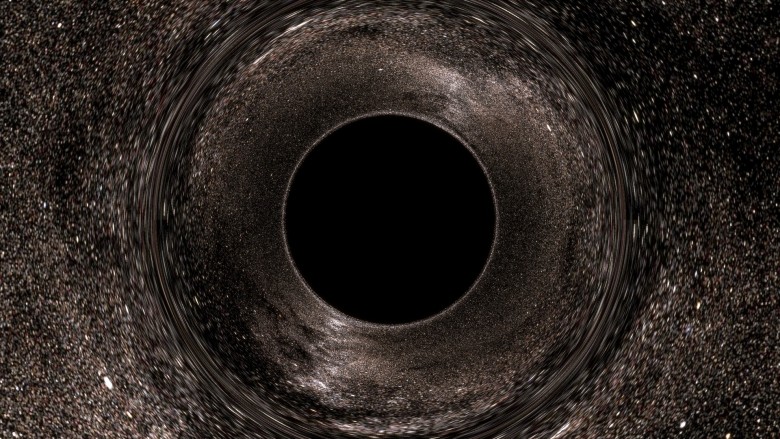
Destaca las características principales: un disco negro y un extraño anillo de distorsión.

Las discusiones a menudo prestan atención: es incorrecto decir que un disco negro es un horizonte de eventos. De hecho, es incorrecto decir que el área de la imagen es un objeto . Esta es una imagen de un objeto. De hecho, hay trayectorias que, al rastrear desde su ojo hasta la fuente, aparecerán en el horizonte de eventos (GS). Estos son píxeles negros, ya que ningún fotón puede seguir este camino desde un agujero negro (BH) hasta su ojo. Por lo tanto, este disco negro es muy claramente una imagen del horizonte de eventos , en el sentido de que si dibujas (en el pasado distante) algo directamente sobre el horizonte, los observadores externos podrán verlo directamente en este disco negro (en realidad ejecutaremos esto experimento más tarde). En algunas publicaciones, esta región negra también se llama la "sombra" de BH.



Sin embargo, es interesante notar que esto también es una imagen de la esfera de fotones (PS). El gráfico gnuplot en la parte superior representa la geodesia de los fotones entrantes desde el infinito (mirando el BH desde una distancia al hacer zoom) junto con GS (negro) y FS (verde). El radio de la esfera de fotones es 1.5 veces mayor que el radio del horizonte de eventos (en la geometría de Schwarzschild) y aquí se permiten las órbitas circulares de los fotones alrededor del agujero negro (aunque inestables). En el gráfico, algunos rayos caen en la inexistencia, mientras que otros están dispersos (y, por lo tanto, aparecen en otro punto de la esfera celeste). Se puede ver que para los rayos absorbidos, el parámetro de exposición es inferior a ~ 2.5 radios. Este es el radio aparente del disco negro, y es mucho más grande que el GS y el FS.

En cualquier caso, el siguiente hecho es importante:

Un rayo de luz que incide libremente en la esfera de fotones también alcanzará el horizonte de eventos.

Esto significa que la imagen de la esfera de fotones está incluida en la imagen del horizonte de eventos. Pero como el GS está claramente ubicado dentro del FS, la imagen del primero también debería ser un subconjunto del segundo. Entonces las dos imágenes deben coincidir.

¿Por qué verificamos que el disco negro también sea una imagen del FS? Porque esto significa que el borde del disco negro está lleno de fotones que se deslizan a lo largo de la esfera de fotones. El píxel inmediatamente fuera del disco negro corresponde a un fotón, que (al trazar hacia atrás) cae en espiral en la esfera de fotones, cada vez más cerca de una órbita circular inestable, girando muchas veces (cuanto más cerca se mira, más rápido gira), y luego aparece en espiral. - ya que la órbita es inestable - y escapa al infinito.

Este comportamiento causará un interesante efecto óptico similar a la separatriz en un sistema dinámico. Teóricamente, si el haz se lanza exactamente a lo largo del borde, girará para siempre en espiral, cada vez más cerca de la órbita circular de la esfera de fotones.

Influencia en la esfera celestial

No nos centraremos en este tema, porque el último applet está dedicado a él, y da una idea mucho mejor de las distorsiones en el cielo (incluida la opción de rejilla UV para distorsiones más claras).

Solo unas pocas palabras sobre el anillo de Einstein. La lente gravitacional es ópticamente distinguible porque es una imagen de un solo punto, que se encuentra directamente opuesto al observador. El anillo se forma en tal ángulo de visión cuando los rayos del observador se doblan en paralelo. Los rayos externos no son lo suficientemente curvos y permanecen divergentes; adentro se doblan demasiado, convergen y, en realidad, incluso pueden ir hacia atrás o en círculo, como vimos.

Pero piense en esto: si se acerca lo suficiente al disco negro, los rayos de luz pueden formar un círculo y luego ir en paralelo. Allí deberíamos ver el anillo secundario de Einstein. De hecho, puede haber anillos de cualquier orden (cualquier cantidad de vueltas). También debe haber anillos "extraños" entre ellos, donde los rayos de luz se doblan en paralelo, pero se dirigen hacia el espectador. Esta serie interminable de anillos existe, pero es completamente invisible en nuestra imagen (de hecho, en la mayoría de estas imágenes), porque está demasiado cerca del borde del disco.

Distorsión del horizonte de eventos

Algo ha cambiado en esta nueva imagen. En primer lugar, está hecho en una mejor resolución y con un filtro de fondo para hacerlo más distinguible. Luego amplié la imagen BH (sin acercarnos, todavía estamos a una distancia de ~ 10 radios de ella, solo un zoom). Pero lo más importante, dibujé una cuadrícula en el horizonte .

El horizonte es "solo una esfera". Técnicamente, no es una esfera riemanniana estándar con una métrica espacial. ¡El horizonte es como la luz! Esta es una manera colorida de decir que viaja a la velocidad de la luz. Sin embargo, en las coordenadas de Schwarzschild, todavía es una superficie $$$r = 1$ y podemos usar $$$\ phi$ y $$$\ theta$ como longitud y latitud. Por lo tanto, una cuadrícula se puede dibujar de forma canónica. La ves en la imagen.

La cuadrícula le permite ver un efecto especial que se puede derivar si analizamos la curva de dispersión / absorción de los fotones arriba:

Toda la superficie del horizonte es visible simultáneamente desde cualquier punto.

Esto es muy interesante Cuando miras una esfera fija en un espacio-tiempo plano estándar, no ves más del 50% de su superficie en ningún momento (si te acercas, es menos del 50% debido a la perspectiva). Pero el horizonte es visible al mismo tiempo que un disco negro: preste atención, en particular, a los polos Norte y Sur. Sin embargo, aunque toda la superficie está colocada en un disco negro, no la cubre por completo : si hace zoom en el borde, verá que la imagen del GE termina al final de la sombra. Encontrará un anillo ubicado muy cerca del borde exterior, pero no hasta el final. Esta imagen es un punto opuesto al observador y define los límites de esta "primera" imagen del HS en su interior. Entonces, ¿qué hay entre este anillo y el borde real? Todavía no he generado una imagen ampliada, pero hay otra imagen completa del horizonte de eventos . Y luego uno más, y uno más, hasta el infinito. Hay infinitas imágenes concéntricas de todo el horizonte, comprimidas en la sombra. (Muchas gracias / u / xXxDeAThANgEL99xXx por señalar este fenómeno que me perdí) .

Agregar un disco de acreción

¿Qué renderización moderna de BH hará sin un disco de acreción? Aunque esta es claramente una pregunta discutible, ¿está Interestelar de Nolan realmente disponible para observación, sin mencionar la precisión, pero definitivamente debemos agradecer al éxito de taquilla por popularizar una distorsión particular del disco de acreción. Aquí tenemos un disco de acreción horizontal infinitamente delgado y plano que se extiende desde la esfera de fotones (aunque esto es poco realista porque las órbitas son más bajas $$$3r_S$ inestable, como se describe a continuación) hasta 4 radios, pintados en una jaula blanca y azul. Con tal color, es obvio que nos enfrentamos a otro caso, cuando al mismo tiempo es visible el 100% de la superficie del objeto.

Para esta imagen, moví el observador un poco más arriba para mirar el disco un poco desde arriba. Verá imágenes de dos caras del disco : la superior y la inferior. La imagen se dobla en un arco sobre la sombra del agujero negro porque el haz dirigido directamente sobre el agujero negro se dobla hacia abajo para encontrarse con la superficie superior del disco detrás del agujero, opuesto al observador.

Esto también explica la existencia misma de la imagen inferior: los rayos que van debajo del BH se doblan hacia la superficie inferior del disco, que está detrás del BH. Si observa de cerca, la imagen se extiende por toda la sombra, pero en la parte superior es mucho más delgada. Esto corresponde a los rayos de luz que van por encima del BH, hacen un círculo casi completo alrededor del orificio y golpean la superficie inferior frente al disco.

Por supuesto, es fácil concluir que hay un número infinito de imágenes de discos de acreción que se diluyen muy rápidamente a medida que se acercan al borde. La siguiente imagen ya es muy delgada, apenas visible en la parte inferior del borde.

Los GIF siguen siendo relevantes

En esta animación convulsiva, enciendo / apago la desviación de la luz (formalmente Schwarzschild / Minkowski) para aclarar algunos de los puntos de los que hablamos.





Estos dos extraños gifs se crean a petición de los lectores. En el primero, el observador gira alrededor de un agujero negro a una distancia de 10 radios. Esto no debe entenderse como una órbita real, ya que en realidad no hay aberración cuando se mueve en órbita. Aquí hay una serie de imágenes BH estacionarias desde varios puntos donde el observador se mueve de un lugar a otro entre cuadros; es una órbita "adiabática", si lo desea.

Y el estéreo sigue siendo relevante

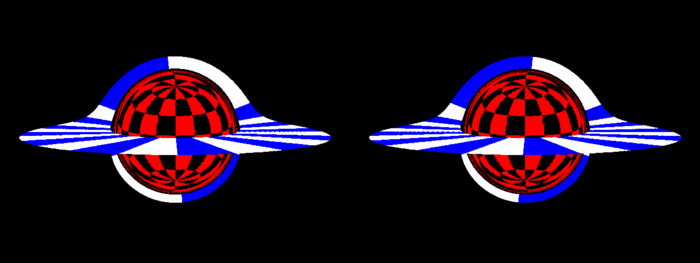
Curiosamente, la sombra se ve bastante plana.

Suficiente ciencia

Tenemos suficientes imágenes informativas al estilo de los años 90 en baja resolución con colores venenosos. Aquí hay algunas representaciones "pop" (haga clic para ampliar).


Esta imagen fue generada por el usuario / n / dfzxh con sobremuestreo cuádruple


Plan más grande


Imagen ampliada del anillo.


El efecto de culto del "anillo de luz" cuando se ve desde el plano ecuatorial


Si descarga el programa, esta es la escena actual por defecto


Un disco mucho más ancho

Pues sí, nada especial. No hay obras de arte, solo representaciones del programa. Volvamos temporalmente a la ciencia: la tercera imagen , que parece no tener significado, es realmente muy valiosa. Esta es el área ampliada entre el borde superior del disco negro y la imagen principal del disco de acreción. El observador está en el borde exterior del disco de acreción y se acerca a la imagen. El objetivo era representar tantos anillos de diferentes órdenes como sea posible. Son visibles tres órdenes: la zona más clara en la parte superior es solo el borde inferior de la primera imagen de la superficie superior lejana del disco. La barra de abajo, debajo del mar tranquilo de estrellas estiradas, es la parte superior de la imagen de la parte frontal inferior del disco. En la parte inferior, una delgada línea de luz con un ancho de no más de un píxel, pegada al disco negro de la esfera de fotones. Esta es básicamente la tercera imagen: nuevamente, la superficie superior distante, pero después de que la luz ha completado una revolución adicional alrededor del agujero negro. Fusionados con él, pero las imágenes cada vez más delgadas son anillos de un orden superior. Bueno, esto también es digno de la etiqueta <blockquote>:

Hay imágenes interminables de las superficies superior e inferior del disco de acreción, y todas muestran la superficie completa del disco al mismo tiempo. Además, a excepción de la primera, estas imágenes no pasan delante del disco negro ni una frente a la otra, y por lo tanto son "concéntricas".

Maravilloso

Acepto solicitudes de renderizado
¿Está interesado en una visualización específica, pero no está listo para pasar por las dificultades de instalar el programa y renderizarse usted mismo? Solo envíeme un reddit o envíeme un correo. Renderizar 1080p en mi computadora portátil no toma más de 10-20 minutos.

Disco de acreción realista

El disco de acreción en las representaciones es bastante caricaturesco. Es solo un estúpido disco de textura. ¿Qué sucede cuando la física real se incluye en la apariencia visual de un disco? ¿Qué sucede cuando considera el desplazamiento al rojo del movimiento orbital, por ejemplo?

Un modelo popular de un disco de acreción es un disco de materia infinitamente delgado en una órbita casi circular. Comienza con ISCO (la órbita circular estable más interna, $$$3r_s$ ) con un perfil de temperatura según una ley de potencia $$$(T \ sim r ^ {- a}$ . Usaré una opción muy simple:

$$

$$T \ sim r ^ {- 3/4}$$

lo cual es definitivamente anormal en la teoría general de la relatividad para fluidos realistas, pero aquí está (en cualquier caso, no notará la diferencia).

Ahora un parámetro libre es una escala común para temperaturas, por ejemplo, la temperatura en ISCO. Esta temperatura es enorme para la mayoría de los agujeros negros. Estamos hablando de cientos de millones de Kelvin; Es difícil imaginar cualquier artefacto humano que pueda existir bajo la influencia de la radiación de disco (pico en la radiación de rayos X) a tales temperaturas, sin mencionar la fotografía. Entonces claramente necesitamos bajar la temperatura. Obviamente, los agujeros negros supermasivos son más fríos, pero no suficientes. Necesitamos bajar a 10,000 K en ISCO para que al menos podamos ver algo. Esto es muy inexacto, pero eso es todo lo que puedo hacer.

Se deben hacer dos preguntas. Primero: ¿de qué color es el cuerpo negro a esta temperatura? Segundo: ¿qué tan brillante es ? Formalmente, la respuesta a estas dos preguntas está en el producto escalar de funciones que describen los canales R, G, B con el espectro del cuerpo negro. En la práctica, se utilizan algunas aproximaciones.

Para la fórmula de Tanner Helland , es precisa y efectiva para el color, pero incluye numerosas condiciones que no son factibles con mi trazado de rayos (ver más abajo para más detalles). La forma más rápida es usar una textura simple:



Esta textura es una de las muchas cosas útiles en la selección de Mitchell Charity de "¿De qué color es el cuerpo negro?" . Como referencia, corresponde al punto blanco E (punto blanco E).

La escala muestra el color de un cuerpo negro a temperaturas de 1000 K a 30 000 K, con temperaturas más altas que corresponden aproximadamente al mismo tono de azul. Dado que existe una gran diferencia en el brillo entre las temperaturas, esta textura no puede ni transmite brillo; más bien, normaliza los colores. Nuestra tarea es calcular el brillo relativo y aplicarlo. Una fórmula analítica es adecuada para esto. Si suponemos que el espectro visible es muy estrecho, la intensidad visible total es proporcional al espectro del propio cuerpo negro:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

donde me libré de las estúpidas constantes comunes (todavía vamos a escalar el brillo para ver algo). Simplemente puedes insertar $$$\ lambda$ aproximadamente para el rango visible del espectro, y obtenemos que el brillo es proporcional a la temperatura de acuerdo con esta fórmula:

$$

$$(e ^ {\ frac {29622.4 \ text {K}} {T}} - 1) ^ {- 1}$$

Es bastante simple. Como verificación, observamos que la intensidad relativa cae rápidamente a cero cuando T se acerca a cero, y prácticamente no cambia cuando T llega al infinito.

Redshift

Discutimos las velocidades orbitales en la geometría de Schwarzschild en la descripción del applet. Para calcular el desplazamiento al rojo, se utiliza la fórmula de desplazamiento al rojo del SRT:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

Donde como $$$\ cos (\ theta)$ - el coseno del ángulo entre la dirección del haz emitido por el disco y la velocidad local del disco, calculado en el sistema de coordenadas de inercia local de Schwarzschild. La fórmula es verdadera en este contexto debido al principio de equivalencia.

Debe multiplicarse por el coeficiente de desplazamiento al rojo gravitacional:

$$

$$(1 + z) _ \ text {Gravitacional} = (1 - r ^ {- 1}) ^ {- 1/2}$$

Este coeficiente no depende de la trayectoria del haz de luz, sino solo del radio de radiación, ya que la geometría de Schwarzschild es estacionaria.

También significa que la contribución de la posición del observador al desplazamiento al rojo gravitacional es constante en todo el campo de visión. Toda nuestra imagen tiene un cambio azul general constante, porque estamos profundamente en BH. Por lo tanto, este efecto proporciona solo un tono tenue que puede ignorarse.

También descuidamos el desplazamiento al rojo del movimiento del observador, porque nuestro observador es estacionario en la geometría de Schwarzschild. Aquí está el resultado final:



Como puede ver, la mayor parte del disco es completamente blanco debido al brillo máximo en los canales de color. Si baja estos canales al rango de 0.0-1.0, entonces las partes externas del disco se volverán pálidas o negras. El aumento de brillo es demasiado grande para ser visto y apreciado.Traté de mostrar el efecto mediante el procesamiento posterior para que las partes más brillantes muestren una transición de color, pero esto no es suficiente.

Bonita foto confusa. Aquí hay una imagen sin tener en cuenta el brillo, donde puede evaluar los colores:



estas imágenes tienen una resolución más baja, ya que se reproducen durante mucho tiempo en mi computadora portátil (las raíces cuadradas son malas, niños).

En cualquier caso, este render es mil veces menos espectacular que los otros (principalmente porque el borde interno del disco ya está lo suficientemente alejado del GS, por lo que la lente es demasiado grande), pero el render es al menos preciso . Si encuentra un agujero negro con una temperatura de 10,000 K y buenas gafas de sol, verá exactamente eso.

Otro primer plano. Elevé de forma antinatural la saturación de la belleza:

Escribir un marcador de rayos de un agujero negro

Fuente de Github

Hay una diferencia muy grande y obvia entre la óptica de los agujeros negros y el integrador numérico, que produce hermosos fondos de escritorio con una resolución de 1080p. La última vez no publiqué mi razonamiento, sino que simplemente planteé un repositorio git grande y sucio. Ahora quiero explicar un poco más en detalle, y también tratar de mantener el código en una forma más precisa y con comentarios.

Mi marcador no fue creado bueno, poderoso, rápido. En primer lugar, quería que fuera fácil de configurar, que fuera simple, para que las personas pudieran inspirarse y ver el potencial de mejora: incluso su imperfección puede alentar a alguien a decidir escribir su propia versión. Aquí hay una breve descripción de los algoritmos y su implementación.

Potencial "mágico"

Entonces, la teoría general de la relatividad, todo está claro. Es facil. Tomamos la métrica de Schwarzschild, buscamos los símbolos de Christoffel, calculamos su derivada, escribimos la ecuación geodésica, cambiamos algunas coordenadas cartesianas para evitar un sufrimiento sin fin, obtenemos una gran EDO de varias líneas, la resolvemos. Algo asi.

Es broma. Por supuesto, hay un truco.

Si recuerdas, la última vez que deduje la siguiente ecuación para la órbita de una partícula sin masa en su plano orbital en la geometría de Schwarzschild ($$u = 1 / r ):$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

El truco es ver la fórmula de Binet aquí . Para una masa de una partícula newtoniana en el potencial newtoniano del campo de fuerzas centrales:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

entonces la partícula obviamente se moverá en su plano orbital y corresponde a la fórmula de Binet para $$$u(\phi)$ :

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

Donde $$dd ϕ es primo$\frac{d}{d\phi}$$$m es la masa, y$m$$$h es el momento angular por unidad de masa. Esta es una ecuación para la órbita, no una ecuación de movimiento. No dice nada sobre$h$$$$u(t)$ o $$p h i ( t ) , solo muestra la relación entre$phi(t)$$$$u$ y $$$\phi$ .

Paremos por un momento para reflexionar sobre lo que realmente tenemos. La ecuación dice que si imagina un sistema mecánico hipotético de una partícula bajo la acción de una determinada fuerza central, entonces su trayectoria será una solución de la fórmula de Binet. Entonces el sistema mecánico se convierte en una calculadora de fórmulas.

Eso es lo que estoy ofreciendo aquí. Hemos indicado$$m = 1 y tomó (no físico, lo que sea) un sistema simple de una partícula puntual en este campo de fuerza particular:$m=1$

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

donde $$h es una constante, y resolver la ecuación numéricamente es muy simple. Entonces la solución$h$$$→ x (T), donde$\vec x (T)$$$$T$ - la coordenada del tiempo abstracto para este sistema es, de hecho, la parametrización de la única solución para la ecuación de Binet correspondiente, que es exactamente la ecuación geodésica .

Por lo tanto, resolvemos la ecuación newtoniana en coordenadas cartesianas, que generalmente es la más simple (decidí usar el método Runge-Kutta para hacer posible aumentar el tamaño del paso y reducir el tiempo de renderizado, pero en el futuro el usuario podrá elegir un método de solución diferente). Luego obtenemos solo la geodesia real similar a la luz, donde $$$T$ ¿El parámetro lo sigue (en contraste con el Schwarzschild $$$t$ , y desde el tiempo normal, que no existe).

Esto es mucho mejor que el método anterior, que funcionaba con coordenadas polares en el plano de la órbita. Aquí los cálculos son muy eficientes.

Ray trazado en numpy

Si observa la fuente, verá un script de Python. Horror! ¿Por qué escribir trazado de rayos en Python? Todos saben cuán lentamente se ejecutan los bucles en Python, que siempre (casi) pone fin al trabajo. El hecho es que realizamos cálculos en numpy, y en paralelo. Es por eso que este programa no podrá mostrar gradualmente en la pantalla partes ya dibujadas: renderiza todo al mismo tiempo.

En primer lugar, creamos una serie de condiciones iniciales. Por ejemplo, una matriz (numPixel, 3) con vectores para todos los píxeles de la imagen (numPixel - ancho de imagen × altura de imagen). Luego, el cálculo de cada rayo se reduce a matrices del tipo (numPixel, ...) . Dado que las operaciones con matrices en numpy son muy rápidas, y todo está tipado estáticamente aquí (espero no decir nada estúpido en este momento), debe calcularse lo suficientemente rápido. Quizás no sea C, pero sigue siendo rápido. Al mismo tiempo, tenemos la flexibilidad y la claridad de Python.

Este método es terrible para el trazado de rayos estándar, donde los objetos tienen partes difusas, reflectantes y refractantes y es importante tener en cuenta las condiciones de iluminación. Por ejemplo, la reflexión selectiva de partes de una serie de rayos es una verdadera pesadilla; El seguimiento de valores booleanos o índices de bucle requiere máscaras múltiples, y los bucles no se pueden romper. Pero aquí hay otro caso: todos los objetos en nuestra escena solo emiten luz: el cielo, un disco de acreción caliente, un horizonte de eventos negro y polvo brillante. No se ven afectados por la luz incidente, y la luz misma también los atraviesa con calma, excepto para reducir la intensidad. Esto nos lleva a un algoritmo para determinar el color:

Mezcla de colores

Esto es fácil: solo necesita mezclar todos los objetos entre nosotros y la fuente del rayo con sus valores alfa correspondientes, y colocarlos uno encima del otro, donde el más alejado estará en la parte inferior. Inicializamos el búfer de color con negro alfa transparente, luego, cuando nos intersectamos con el objeto, actualizamos el búfer mezclando el color del objeto debajo de nuestro búfer de color. Realizamos los mismos pasos para el polvo (use el perfil de densidad $$$r ^ {- 2}$ ) y continuar iterando hasta el final. Tenga en cuenta que el canal alfa también funciona como un búfer Z, ya que el objeto deja de contribuir después de que el rayo cruza el objeto opaco (lo que establece el valor alfa del búfer en 1.0).

El inconveniente obvio de este método es que no puede detener el trazado de rayos después de calcularlo, porque es parte de la matriz donde continúa el rastreo de otros rayos. Por ejemplo, después de una colisión con el horizonte, los rayos continúan deambulando aleatoriamente después de haber caído en una singularidad: puede ver qué sucede si apaga explícitamente el objeto del horizonte. El algoritmo de mezcla alfa garantiza que no afecten a la imagen final, pero estos rayos aún cargan la CPU.