Sigo familiarizando a los lectores de Habr con los capítulos de su libro "Teoría de la felicidad" con el subtítulo "Fundamentos matemáticos de las leyes de la maldad". Este libro de ciencia popular aún no se ha publicado, informa de manera muy informal acerca de cómo las matemáticas le permiten mirar el mundo y la vida de las personas con un nuevo grado de conciencia. Es para aquellos que están interesados en la ciencia y para aquellos que están interesados en la vida. Y dado que nuestra vida es compleja y, en general, impredecible, el énfasis en el libro se centra principalmente en la teoría de la probabilidad y las estadísticas matemáticas. Aquí no se prueban los teoremas y no se dan los fundamentos de la ciencia, de ninguna manera es un libro de texto, sino lo que se llama ciencia recreativa. Pero es precisamente un enfoque tan lúdico que nos permite desarrollar la intuición, alegrar las conferencias para los estudiantes con ejemplos vívidos y, finalmente, explicar a los no matemáticos y a nuestros hijos que encontramos cosas tan interesantes en nuestra ciencia seca.En este capítulo, analizaremos el dinero, los mercados y la entropía, así como también los gifs animados, que, por desgracia, no se pueden imprimir en un libro.
Observación de Hongren:
Entre los economistas, el mundo real a menudo se considera un caso especial.
La economía es una ciencia grande, seria, pero peculiar. Sin duda, es de vital importancia como disciplina que estudia el fenómeno real e importante de nuestro mundo: la realidad económica. La ciencia económica se esfuerza por la comprobabilidad y la formalización, tiene muchas matemáticas, a veces complejas e interesantes. Sin embargo, al abrir un libro de texto económico serio, lo más probable es que encuentre algunos cálculos relativamente simples, recetas preparadas y un montón de razonamientos informales con este espíritu: "pero, de hecho, todo puede estar mal y, en general, como quiera, si eso sucede la voluntad de jugadores clave o del gobierno ". Al final, uno puede tener la sensación de que la intuición, el conocimiento de la psicología y la capacidad de percibir el contexto general son más importantes en esta disciplina que el cálculo preciso y la consideración meticulosa de los detalles (se trata de economía, no de contabilidad). Finalmente, casi la mitad de las disertaciones falsas están escritas específicamente sobre economía; por lo tanto, no es tan difícil discutir razonablemente sobre temas económicos. También probaremos nuestra fuerza en este campo, bien, en ningún lugar la injusticia de este mundo es más grave que en la cuestión de la distribución de la riqueza. Además, no importa en qué se dedica una persona, no importa qué profesión posea, está involucrado en la economía y sus juegos, desde las leyes de la economía, así como desde las leyes de la física, para no esconderse.
De toda la masa de problemas resueltos por la economía matemática, consideraremos solo uno: cómo resulta que, incluso en igualdad de condiciones para todos los participantes del mercado y un intercambio justo de fondos, los pobres se vuelven más ricos que los ricos y por qué incluso una sociedad matemática ideal es propensa a la desigualdad financiera. Bueno, en el camino aprendemos algo interesante sobre estadísticas matemáticas y distribuciones de variables aleatorias.
Soy físico por educación y por profesión, y mi deformación profesional se expresa en una visión peculiar del mundo, como en una variedad de diferentes sistemas y procesos físicos. Desde el punto de vista de un físico, el mercado real es un sistema abierto sustancialmente no estacionario, con muchos grados de libertad, en el que los procesos estocásticos (aleatorios) juegan un papel importante. En este sentido, el mercado es similar al tema de estudiar ramas de la física como la termodinámica y la física estadística, en las que, en vista de la imposibilidad de considerar todos los innumerables detalles y el comportamiento de todos los componentes del sistema, cambian a propiedades generalizables y medibles, como la energía, la temperatura o la presión. . No es sorprendente que los intentos de describir termodinámicamente los sistemas económicos y crear econofísica se hayan llevado a cabo durante más de cien años. Pero el problema es que: mientras los científicos consideran los detalles, resumen el conocimiento adquirido y discuten sobre las leyes fundamentales, el principal objeto de estudio es la realidad económica y tiene tiempo para cambiar más allá del reconocimiento. Su comportamiento parece buscar preservar, o incluso aumentar su incertidumbre e imprevisibilidad.
Un buen ejemplo es la historia de dos siglos de usar el análisis técnico cuando se juega en la bolsa de valores. Cuando aparece una nueva herramienta poderosa que le permite buscar patrones ocultos y predecir el precio de un valor o stock, comienza a generar ganancias para aquellos que lo usan. Pero pronto el mercado comienza a "sentir" nuevos jugadores y a adaptarse a su estrategia, la precisión de las predicciones del maravilloso método comienza a caer y, después de un tiempo, cae en una gran lista de herramientas obsoletas y poco confiables. Ni los modernos algoritmos de redes neuronales de autoaprendizaje flexibles ni los operadores de robots súper rápidos que realizan millones de operaciones por minuto han cambiado la propiedad principal del juego de la bolsa en las últimas dos décadas: su imprevisibilidad. Y hasta ahora, las principales ventajas de un profesional en esta industria son voluntad, resistencia de carácter, aversión a la pasión ... bueno, o propiedad del intercambio. ¡Todo es como en un casino donde los juegos se basan en pura casualidad! Por un lado, esto, por supuesto, es insultante y, por otro, brinda la oportunidad de mejorar constantemente los métodos y enfoques. Érase una vez, tanto la teoría de la probabilidad como las estadísticas matemáticas nacieron de los intentos de analizar el juego y los juegos económicos, y solo entonces encontraron aplicación en casi todas las ciencias naturales.
En una discusión adicional, hablaremos sobre el dinero, pero esta categoría familiar de uso cotidiano es sorprendentemente compleja y ambigua. El significado y el valor del dinero dependen de muchos factores, y fuera de contexto llamando a una cierta cantidad de dinero, no decimos nada sobre su valor real. Esto distingue los valores monetarios de la mayoría de las cantidades físicas que describen nuestro mundo y dificulta la realización de debates rigurosos en la economía. Pero el propósito de nuestra conversación: los fundamentos matemáticos de las leyes de la mezquindad, cotidianas, comprensibles y simples. Por lo tanto, en el futuro hablaremos de algunos "rublos", refiriéndonos a un boleto o moneda formal, e implicando que mientras más personas tengan "rublos", más ricos serán. Otras discusiones sobre el poder adquisitivo, valores intangibles o ilíquidos, y "la felicidad no está en el dinero", finalmente, lo dejaremos fuera de la conversación.
¡Vamos, para!
Comenzamos analizando la justicia de algunas estrategias simples para distribuir una cierta cantidad de dinero a un grupo finito de personas.
La primera estrategia más obvia: "tomar todo y dividirlo", es decir, dar a cada miembro del grupo una parte igual de la cantidad total. Tal distribución se llama
degenerada , tiene un índice de Gini igual a cero y corresponde a una curva de igualdad en el diagrama de Lorentz.
Distribución de dinero absolutamente justa y degenerada: todos están igualmente divididos.¡Gran opción! Lo llamaremos
"estrategia de Sharikov" en honor al héroe de la novela de Mikhail Bulgakov "Corazón de perro", que propuso de esta manera resolver todos los problemas económicos.
La segunda estrategia más realista es distribuir a todos un rublo al azar. Quien tiene suerte. Podemos llamar a esta estrategia
"Poisson" , ya que así es como los eventos aleatorios independientes en el proceso de Poisson se distribuyen en la escala de tiempo. Para un grupo de
n persona la probabilidad de que cada uno de los participantes reciba el rublo es
1 / n . Después de la distribución de esta manera
M rublos, todos deberían recibir una cantidad igual al número de tales resultados "positivos". La función de probabilidad para tal suma es bien conocida: es una
distribución binomial , similar a una campana, que se dispersa simétricamente alrededor del valor promedio
M / n . Por lo general, se lo presentan calculando la probabilidad de obtener la cantidad indicada lanzando dados. Para grandes valores
M la distribución binomial se vuelve casi indistinguible de lo normal. Veamos cómo cambiará, a medida que se distribuya el dinero, la distribución del dinero en el grupo y su equidad.
El resultado de la distribución del dinero según el principio de "a quién enviará Dios" es una distribución binomial. Cuanto más dinero entregamos, mayor es el valor del promedio y el spread, pero la probabilidad de no obtener nada casi desaparece.Algoritmo de estrategia de PoissonDatos iniciales : xs - una matriz de n elementos llenos de ceros, M - la cantidad total de dinero en el sistema.
M i <- 1 n xs[i] <- xs[i] + 1
Esta distribución, desde el punto de vista de la justicia, se ve muy bien, además, ¡se vuelve más justa cuanto más dinero le damos al público! Simplemente genial! Es una pena que la sociedad no esté organizada de la misma manera y que la lluvia no derrame dinero sobre todos por igual.
Para completar la imagen, veamos otra distribución artificial simple de dinero:
uniforme . Con esta distribución los pobres serán tanto como los ricos.
La distribución uniforme no significa que el dinero se distribuya de manera uniforme entre todos. Con esta distribución, el número de campesinos ricos, pobres y medios es el mismo, pero el dinero pertenece principalmente a los ricos.Algoritmo de estrategia de distribución uniformeDatos iniciales : xs - una matriz de n elementos llenos de ceros, M - la cantidad total de dinero en el sistema.
x xs x <- 0 M/n
Para una distribución uniforme, la curva de Lorentz es una parábola cuadrática, y si el límite izquierdo de la distribución es cero, entonces esta parábola es independiente de la posición del límite derecho, y el índice de Gini para todas esas distribuciones es exactamente
1 / 3 . Tal valor de índice (¡pero no tal distribución!) Estaba, por ejemplo, en la economía australiana en la década de 2000; este es un indicador bastante bueno.
Sin embargo, el mercado es el mercado! Las distribuciones consideradas anteriormente son buenas, pero requieren condiciones especiales para su ocurrencia. Si le da a la gente la libertad de intercambiar dinero, cambiar dinero por servicios, guardarlo y gastarlo en una noche, las distribuciones ideales perderán estabilidad y se convertirán en otras.
¡Nueva política económica!
Considere un grupo de
n la persona Como resultado de la revolución, distribuiremos a todos los participantes en el experimento una cantidad igual de dinero, por
m rublos a todos, habiendo recibido la distribución más justa de fondos Sharikov en la sociedad. Ahora les daremos la libertad de hacerse ricos y empobrecidos por la voluntad de su propio destino y construir un modelo de mercado primitivo. Le pedimos a alguien seleccionado al azar que le dé un rublo a cualquier persona en el grupo que también fue seleccionado al azar. Digamos que esta es la compra de un determinado servicio a un precio fijo. Se espera que la distribución de la riqueza cambie: alguien tendrá menos dinero, alguien más. Repitamos el procedimiento de intercambio una y otra vez y veamos cómo cambiará la distribución de la riqueza en el grupo.
Es prudente reflexionar sobre lo que esperamos ver antes de realizar el experimento. El intercambio de dinero entre los participantes es igualmente probable, como en el caso de la estrategia de Poisson de distribuir dinero, pero al mismo tiempo, los jugadores pierden dinero, además, de acuerdo con el mismo principio de Poisson y con la misma intensidad. Por lo tanto, se puede suponer que los incrementos positivos y negativos se distribuirán normalmente y se ubicarán simétricamente con respecto a cero. Cada jugador, al final, recibirá una diferencia de estos incrementos, que para dos variables aleatorias normalmente distribuidas también se distribuirán normalmente, en este caso, alrededor de cero, ya que las pérdidas y las ganancias son simétricas.
Después de muchos intercambios, cada jugador recibirá y perderá una cantidad que obedece a una distribución cercana a lo normal. Los ingresos totales también se distribuirán normalmente alrededor de cero.Por lo tanto, obtenemos una caminata aleatoria clásica con incrementos distribuidos normalmente y podemos esperar cierta difusión de fondos alrededor de la media
m . La función de probabilidad debe ser borrosa, aumentando la varianza a un valor promedio constante. Todo parece ser simple.
Pero hay un matiz. Si, por alguna razón, a alguien del grupo no le quedan fondos, no podrá comprar servicios dando dinero, pero, al mismo tiempo, puede recibirlo. El posible valor de la riqueza está limitado a cero a la izquierda, lo que significa que la difusión de la riqueza no puede extenderse indefinidamente, y la función de probabilidad observada, tarde o temprano, dejará de ser simétrica.
Hay un matiz más. La cantidad de dinero en nuestro sistema cerrado es limitada e invariable, lo que significa que las caminatas aleatorias no son independientes. Algún jugador afortunado podrá obtener grandes cantidades y alejarse mucho del conjunto, pero solo si la masa total se vuelve más pobre. Los participantes del experimento son unidos por una red invisible por la ley de ahorrar dinero en el sistema. ¿Para qué se esforzará la distribución del dinero en tales condiciones? Parece que la respuesta no es tan obvia como podría parecer a primera vista, pasemos a la simulación y veamos qué sucede.
Resultado de la simulación para compartir una cantidad igual de dinero por n = 1000 y m = 100 . Al principio, de hecho, se observa un fenómeno similar a la difusión, pero a medida que la función de probabilidad alcanza el límite izquierdo, la distribución tiende a una forma asimétrica y no muy característica con un coeficiente de Gini cercano a 0.5 0.5 .Algoritmo de igual cantidadDatos iniciales : xs : una matriz de n elementos, inicializados con m valores.
i <- 0 n xs[i] > 0 j <- 0 n xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
Si un físico lee este libro, entonces podrá asumir con confianza que esto podría ser una distribución; lo llamará la distribución de Gibbs. Un lector atento puede recordar que ya nos hemos encontrado con una imagen similar y con ese índice de Gini cuando examinamos la frustración mientras esperábamos un autobús. Luego examinamos la distribución de intervalos entre eventos de Poisson, que se describió mediante una distribución exponencial. Ambos caballeros astutos estarán en lo cierto, llamando a diferentes nombres con la misma distribución maravillosa.
Las personas son moléculas
La distribución de Gibbs es del campo de la física estadística. Describe las propiedades de los sistemas llamados la hermosa palabra "conjunto", que consisten en una gran cantidad de elementos que interactúan, con mayor frecuencia partículas. En el conjunto, puede seleccionar subsistemas arbitrarios (por ejemplo, partículas individuales o sus grupos) y asignarles ciertas funciones de estado (estas pueden ser coordenadas generalizadas, velocidades, concentraciones, potenciales químicos y mucho más). Utilizando los métodos de la física estadística, es posible explicar y calcular los parámetros de una amplia variedad de fenómenos: procesos químicos y catalíticos, turbulencia, ferromagnetismo, comportamiento de cristales líquidos, superfluidez y superconductividad, y muchos otros.
La distribución de Gibbs responde a la pregunta: ¿cuál es la probabilidad de cumplir un cierto estado del subsistema si a) se le da la energía del estado, b) las propiedades macroscópicas (relativamente hablando, globales) del sistema, como la temperatura, yc) ¿se sabe que el sistema está en equilibrio termodinámico? Se puede expresar esquemáticamente de la siguiente manera:
p m a t h r m G i b b s ( T ) ( x ) = C e - f r a c E ( x ) k T ,
donde
x - un cierto estado del subsistema,
E ( x ) Es la energía de este estado,
T Es la temperatura absoluta del sistema (o su análogo), y
C y
k - valores necesarios para la normalización y conformidad de las dimensiones. La condición de equilibrio es muy importante, significa que el tiempo desaparece de la consideración y que todo el sistema estará en su estado más probable para las condiciones dadas.
No necesitamos una derivación rigurosa de la expresión para la distribución de Gibbs aquí; en cambio, quiero mostrar un hermoso razonamiento puramente matemático que conduce a su forma exponencial. Como consideramos las partes del sistema que se suman a todo el sistema, vale la pena elegir una cantidad
aditiva como su característica, es decir, que su valor para el conjunto sea la suma aritmética de los valores de sus partes. La energía se puede utilizar como tal cantidad en mecánica. Por otro lado, calculamos la probabilidad de observar un cierto estado del sistema, y la probabilidad es
multiplicativa , es decir, si el sistema se puede dividir en partes, entonces la probabilidad de observar todas estas partes al mismo tiempo será igual al producto de las probabilidades para el estado de cada una de las partes. Por lo tanto, necesitamos una función que convierta una cantidad aditiva en una multiplicativa. Solo la función exponencial tiene esta propiedad.
a x , la suma de los argumentos se convierte en un producto de valores:
a x + y = a x a y . Bueno, de todas las funciones exponenciales, la más conveniente es el exponente, ya que se comporta muy bien cuando está integrado y diferenciado.
En nuestro modelo de mercado, tenemos una cantidad aditiva: la cantidad de dinero que tiene cada jugador, esto es un análogo de la energía. En el intercambio descrito por nosotros, esta cantidad, como la energía en el sistema físico, se conserva. ¿Y cuál es el punto de temperatura? Es fácil de averiguar mirando la expresión para la densidad de probabilidad de la distribución exponencial:
p mathrmExp( lambda)(x)= lambdae− lambdax,
y recordando que el promedio para él es
1/ lambda . Dado que el número de jugadores durante el proceso de licitación no cambia, la cantidad promedio aritmética de dinero de los jugadores es igual a la cantidad inicialmente distribuida
m . Se sigue naturalmente que
lambda=1/m , entonces la cantidad promedio de dinero de los jugadores actúa como la temperatura en nuestro modelo económico. En un mercado “calentado” con gran liquidez, podremos observar una mayor expansión en el nivel de bienestar que en un “frío”, porque la dispersión en la distribución exponencial es
1/ lambda2 . Como dijo Ostap Bender en el "Becerro de oro" de I. Ilf y E. Petrov: "Una vez que algunos billetes deambulan por el país, debe haber personas que tengan muchos".
Para ser absolutamente precisos, y recordar que el dinero en nuestro experimento es una cantidad discreta, entonces observamos una distribución
geométrica , un análogo discreto de exponencial. Ocurre en el problema de contar el número de fallas antes de la primera victoria cuando se lanzan monedas de diversos grados de honestidad. Estas dos distribuciones son similares y se vuelven indistinguibles con una disminución en la probabilidad de ganar. En nuestro experimento, las posibilidades de obtener el rublo son iguales
1/1000 , es lo suficientemente pequeño como para llamar a la distribución exponencial.
Queda por tratar con el equilibrio del estado final del mercado. El equilibrio termodinámico se puede describir de varias maneras. En primer lugar, el estado
estacionario debe estar en
equilibrio , en el cual el sistema puede permanecer indefinidamente, sin cambiar sus parámetros macroscópicos, y sin formar flujos ordenados de materia y energía dentro de sí mismo. En segundo lugar, debe ser
estable , es decir, si el sistema no está equilibrado, tenderá a volver a él. En tercer lugar, este es el estado más probable del sistema, observado con mayor frecuencia, en el que con el tiempo el sistema tenderá a pasar de cualquier otro estado de no equilibrio. Nuestro experimento demuestra estos criterios para el equilibrio: habiendo llegado a una distribución exponencial, el sistema permanece en él, y además, es fácil asegurarse en el experimento de que desde cualquier distribución arbitraria, después de algún tiempo, volvamos a ser exponencial. Pero esto no es una prueba, sino solo una pista de que lo más probable es que estemos tratando con el equilibrio. Necesitamos algún tipo de criterio formal medible que nos indique inequívocamente que el sistema está en equilibrio sin la necesidad de esperar indefinidamente o de clasificar todas las distribuciones iniciales posibles. Este sería un criterio útil que podría aplicarse al mercado real, sin la necesidad de realizar experimentos arriesgados con personas vivas.
Tao expresado en palabras - no es cierto Tao
Las reflexiones sobre el equilibrio llevaron a los físicos al concepto de
entropía , que gradualmente fue más allá de la termodinámica y fue tan apreciada por los científicos de todas las direcciones, los filósofos y el público en general, que ahora la entropía ha recibido un aura de misterio, incomprensibilidad y Dios sabe algo más. Un concepto simple y especial, en esencia, ganó una reputación en las mentes de las masas como un concepto mundial inexplicablemente gobernante. Esto se debe al hecho de que la termodinámica es una ciencia universal que describe a un nivel muy alto de abstracción un sistema de una naturaleza muy diversa: desde física, química y biológica hasta social, económica e incluso puramente humanitaria. Después del curso escolar, sin embargo, sigue existiendo la sensación de que la termodinámica se trata de un gas ideal aburrido, algunos pistones y un ciclo de Carnot imposible. Una visión tan unilateral está relacionada con el hecho notable de que la termodinámica, siendo una de las ramas más abstractas y universales de las ciencias naturales, resuelve elegantemente problemas aplicados que son comprensibles para los escolares y útiles en la industria. Esto no se puede decir, por ejemplo, sobre la teoría de categorías o la topología, que también son disciplinas muy abstractas, universales e indudablemente útiles, pero casi nunca se encuentran en las tareas cotidianas.
Entonces la entropía. El creador de la termodinámica, Clausius, y más tarde Gibbs y Boltzmann, requirió una característica cuantitativa del equilibrio, que indica la probabilidad de observar el estado indicado del sistema o sus partes. Además, este valor, que refleja una probabilidad de naturaleza multiplicativa, debe ser una función de estado aditivo para que pueda calcularse para el sistema sumando los valores calculados para sus partes. Cuando buscamos una función adecuada para la distribución de Gibbs, procedimos del hecho de que debería convertir un argumento aditivo en un valor multiplicativo. Al buscar una expresión para entropía, necesitamos una función que sea multiplicativa en argumento y aditiva en valor; esta es una función logarítmica, la inversa de la exponencial. La entropía del estado de un sistema complejo se puede expresar como el valor esperado para el logaritmo de la probabilidad de observar el estado de todas sus partes, o, según Boltzmann, como el logaritmo de la cantidad de formas en que se puede realizar este estado del sistema. En este caso, el estado más probable corresponde a un mayor valor de entropía, y al estado de equilibrio, el máximo posible.
La cantidad de formas de realizar este o aquel estado depende de la cantidad de restricciones o condiciones bajo las cuales se puede realizar este estado. Cuantas menos restricciones, más probable es el estado y mayor es el valor de su entropía. Estas restricciones y condiciones tienen sentido de la
información de estado. De ahí la idea de que la entropía refleja el grado de nuestra ignorancia del sistema: cuanto menos sepamos sobre el estado, mayor será su entropía. Shannon luego generalizó este concepto para cualquier sistema que contenga información, incluso para distribuciones de variables aleatorias. Esto es lo que hizo: para una variable aleatoria
X definido por una función de probabilidad
p(x) la entropía se define de la siguiente manera:
H(X) equiv− mathrmM( ln(p(x)))=− sump(x) ln(p(x)),
donde la suma se realiza sobre todos los valores
x en el cual
p(x)>0 . Por lo tanto, podemos calcular la entropía del estado de cualquier sistema complejo, teniendo su descripción estadística.
Así es como cambia la entropía a medida que nuestro modelo de mercado llega al equilibrio.
El crecimiento de la entropía a medida que el mercado se acerca al estado de equilibrio. La línea horizontal en el gráfico de la derecha muestra el valor teórico de la entropía para la distribución exponencial, igual a 1− ln( lambda) . El "estante" intermedio corresponde al período durante el cual la distribución pasó por la etapa de difusión y parecía normal.Por lo tanto, cada distribución: definida analíticamente u obtenida experimentalmente en forma de histograma, puede asociarse con un número positivo: su entropía. Esto significa que las distribuciones pueden compararse entre sí, determinando más o menos equilibrio y probable para condiciones dadas. Además, para una cierta clase de distribuciones es posible distinguir una distribución con entropía máxima, además, solo una. Las clases se definen por restricciones o la medida de nuestro conocimiento de las propiedades estadísticas de un sistema. Aquí hay algunos ejemplos:
| ¿Qué sabemos sobre la variable aleatoria? X | distribuciones con entropía máxima |
|---|
| X en[a,b] | uniforme sobre el corte [a,b] |
| X \ in \ {0,1 \} | Distribución de Bernoulli |
| X en[0, infty) + promedio | exponencial, para una cantidad discreta - geométrica |
| X en[xm, infty) + media geométrica | Distribución de Pareto (potencia) |
| X en[0, infty) + promedio + media geométrica | distribución gamma |
| X en[0, infty) + media geométrica + varianza para la media geométrica | registro normal |
| X in(− infty, infty) + media + varianza | normal |
Familiar todas las caras! Estas son distribuciones muy utilizadas que los estadísticos aplican a la clase más amplia de tareas. Su universalidad se debe precisamente al hecho de que, teniendo la máxima entropía, son más probables y observables. Para ellos, como equilibrio, tienden muchas distribuciones de variables aleatorias reales. El más libre de restricciones entre todos los demás es la distribución normal: requiere un mínimo de información sobre una variable aleatoria. Menos fallará: si indicamos solo el valor promedio, entonces, en un esfuerzo por aumentar la entropía, la distribución se “difuminará” a lo largo de todo el eje numérico.
Pero, si conocemos solo el valor promedio, pero al mismo tiempo limitamos la variable aleatoria a valores positivos, entonces la distribución de equilibrio será inequívoca: exponencial. Es este caso el que observamos en nuestro experimento con el mercado. Sabíamos de antemano cuánto dinero le dimos a cada jugador y el hecho de que la cantidad de dinero en el sistema era constante, esto fijó un valor promedio. Y dado que nuestro dinero es positivo, muy probablemente, en equilibrio, obtenemos la distribución exponencial de la riqueza con el índice de Gini igual a1 / 2 .
Hay muchas modificaciones del modelo descrito por nosotros: el intercambio puede tener lugar no en un rublo, sino en un valor aleatorio limitado por el estado del donante, mientras que es posible dar dinero no a ningún jugador, sino distribuirlo al azar. Hasta que introduzcamos nuevos parámetros en el juego, todas estas modificaciones no cambian la forma de la distribución de equilibrio de la riqueza, sigue siendo exponencial. Puede verificar esto con la ayuda de la simulación, pero no es interesante dar imágenes para varios métodos de intercambio: todos son iguales. Muchos investigadores han notado esta característica de los modelos de mercado. Un modelo interesante es el construido por Dragulescu y Yakovenko de la Universidad de Maryland, en el que los jugadores se combinan en ciertas compañías y luego se simula la interacción de las compañías con los jugadores-trabajadores y jugadores-compradores.Pero incluso en este caso complejo, el equilibrio es la distribución exponencial, que es indiferente a los parámetros elegidos del modelo.Para demostrar la universalidad del principio de máxima entropía, limitemos artificialmente el nivel de riqueza de un jugador individual desde arriba, prohibiéndole recibir dinero si ya tiene una cierta cantidad fija. La distribución de equilibrio, por supuesto, cambiará. Y en caso de que el borde derecho sea igual al doble del valor promedio, entonces llegamos al caso descrito en la primera fila de la tabla. De hecho, al limitar la variable aleatoria a un segmento finito y no indicar nada más, no podemos asumir ningún otro valor esperado del promedio, excepto el medio de este segmento. Por lo tanto, la distribución de equilibrio con esta opción debe ser uniforme. ¿Vamos a ver si esto es así?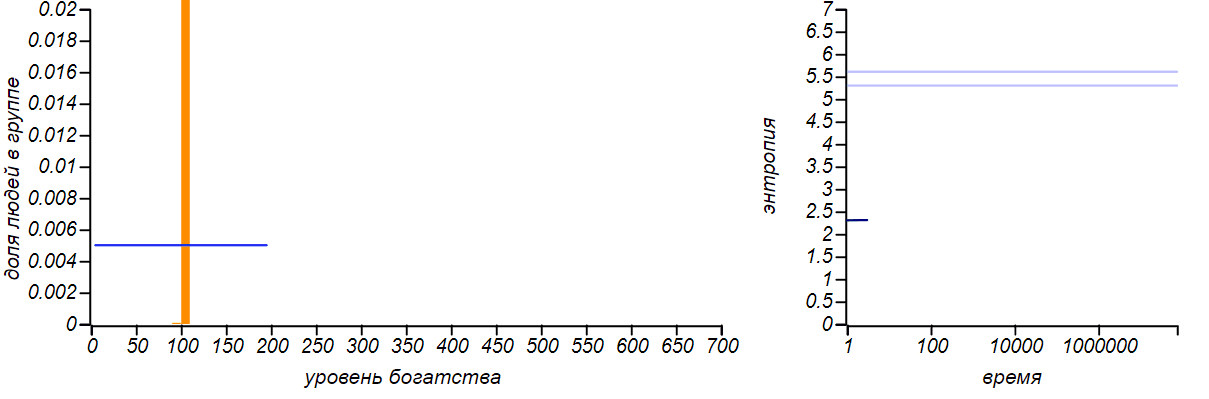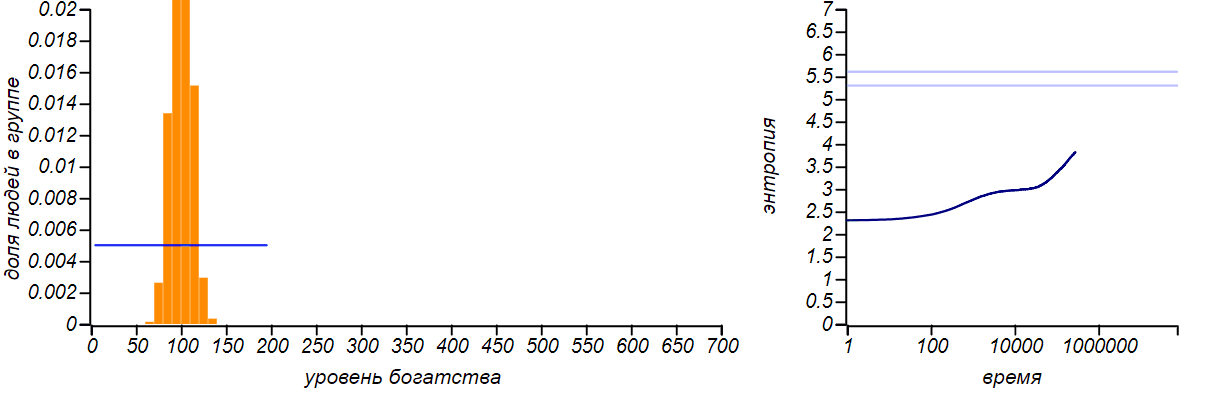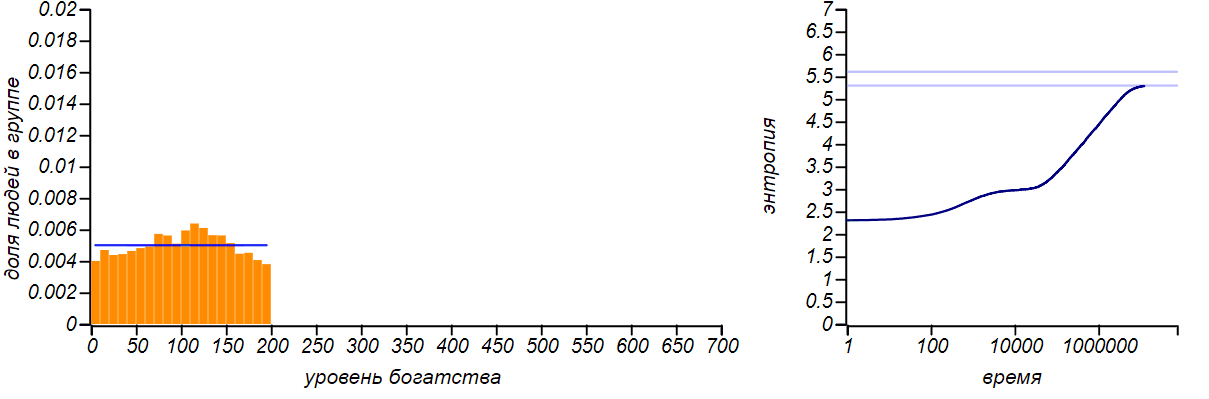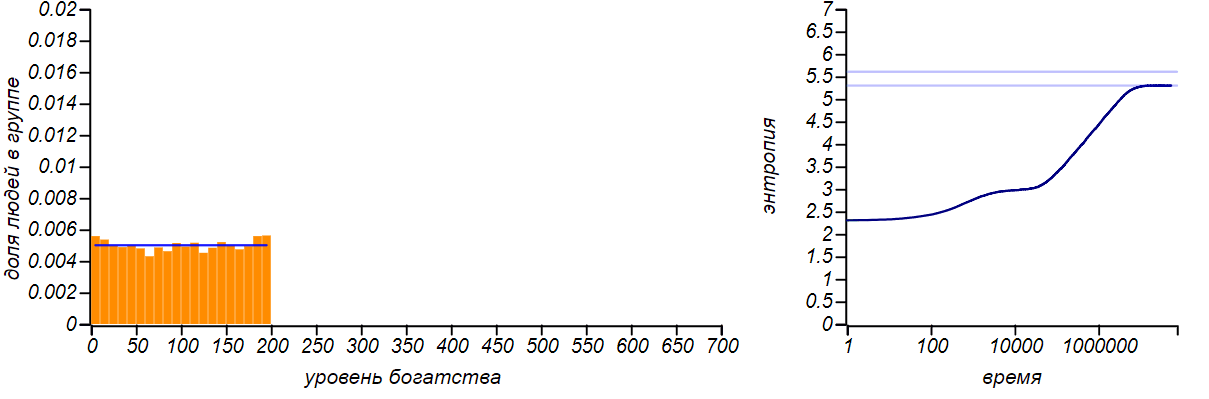
Algoritmo para intercambiar cantidades iguales con una restricción en la parte superior: xs — n , m , xMax — .
i <- 0 n xs[i] > 0 j <- 0 n xs[j] < xMax xs[i] <- xs[i] - 1 xs[j] <- xs[j] + 1
¿Y qué sucederá si se rompe la simetría, es decir, si movemos el borde derecho hacia la derecha o hacia la izquierda?<\ br>Variantes de distribuciones acotadas asimétricas en comparación con distribuciones de Bernoulli correspondientes al desplazamiento del valor promedio. Las líneas horizontales en los gráficos de entropía indican los valores teóricos para la entropía de las distribuciones de Bernoulli.La distribución de la riqueza dejó de ser uniforme, tomando la forma de una exponencial limitada. Con el desplazamiento de la frontera derecha hacia la izquierda, el equilibrio de jugadores ricos se volvió más que pobre. Si "endurecemos" el histograma con solo dos columnas restantes, obtenemos la distribución de Bernoulli que muestra la probabilidad de que sea condicionalmente "pobre" o "rico". Cuando los valores de una variable aleatoria se limitan a solo dos valores, la distribución de Bernoulli es la única opción; por supuesto, ofrece un máximo de entropía. Pero preste atención al hecho de que la entropía de las distribuciones de nuestro modelo tiende precisamente a los valores predichos por la distribución de Bernoulli. Los coeficientes de Gini para estos dos casos son iguales0,43 y
0.2 , respectivamente.La entropía misteriosa y poderosa es, por supuesto, genial y, quizás, incluso convincente. Pero ¿por qué, con un intercambio simétrico, los pobres se vuelven más ricos que los ricos? ¿Por qué el modo de distribución de equilibrio es igual a cero? Es necesario, como dicen los físicos, comprender la cinética del proceso, es decir, el destino de las partículas individuales. No nos equivocamos al suponer que el modelo de caminata aleatoria describe un cambio en el estado de un postor individual: es igualmente probable que tome medidas tanto hacia arriba como hacia abajo. Y para la caminata aleatoria se cumple una famosa ley de la mezquindad: la maldición del jugador. Permítame recordarle que consiste en el hecho de que con una observación lo suficientemente larga, una partícula que vaga al azar necesariamente estará en cualquier lugar indicado de antemano.Además, la distancia a la cual la partícula se aleja de cualquier punto de partida es proporcional a la raíz cuadrada del número de pasos. Todo esto lleva al hecho de que si una partícula comienza su camino cerca de cero, lo más probable es que lo alcance, y dado que el cero en nuestro problema es un límite impenetrable, se verá obligado a comenzar su camino una y otra vez cerca del punto cero, experimentando La notoria maldición. A medida que la partícula se aleja de cero, la probabilidad de regresar a ella disminuye y los ricos se vuelven más propensos a salvar su condición. Pero entonces, ¿qué impide que la partícula se aleje arbitrariamente lejos y que un jugador en particular se vuelva arbitrariamente rico? De hecho, nada más que la finitud del dinero en el sistema: la distribución exponencial es diferente de cero en todo el eje positivo.Pero para lograr una riqueza increíble de acuerdo con las reglas de nuestro juego, es necesario que todos los jugadores seleccionen aleatoriamente al mismo jugador una y otra vez. Y por primera vez, la probabilidad de tal elección es( 1 / n ) n - 1 es la milmillonésima parte de un grupo de diez personas, y es increíble repetirlo muchas veces por accidente. La elección de a quién dar dinero en nuestro modelo es igual para todos, lo que significa que no solo se hará rico sino también pobre. ¡Hay justicia en este mundo! Aunque triunfante no por mucho tiempo, si no eres rico.La economía debe ser económica.
Mientras nuestro modelo de intercambio no tenga en cuenta la prosperidad de los jugadores, seguirá siendo poco realista. De hecho, los ricos gastan más y los pobres gastan menos, además, las personas razonables intentan mantener una parte de su fortuna. Como la próxima complicación del modelo, solicitemos que los jugadores den una cierta participación conocida al intercambiarα de su condición. Un nuevo parámetro y una nueva restricción se introducen en el sistema, por lo tanto, el estado de equilibrio puede desviarse del exponencial. Usando fracciones del nivel de bienestar, pasamos a características multiplicativas, como, por ejemplo, retorno de la inversión, retorno de la inversión, etc. Todos los libros de texto de economía indican que si desea calcular el rendimiento promedio de la inversión, por ejemplo, durante muchos años, debe calcular la media geométrica de los rendimientos de cada año. En nuestro caso, la media geométrica es única, aunque no trivial, determinada por el valorα .
Por lo tanto, al agregar un nuevo parámetro, fijamos la distribución media geométrica de los ingresos de los jugadores, o el rendimiento promedio del modelo de mercado. Por lo tanto, podemos esperar que la distribución de equilibrio de la riqueza esté bien descrita por la distribución gamma. Podemos estar convencidos de ello, habiendo llevado a cabo modelos de simulación.Si los costos del intercambio son proporcionales a la abundancia, la distribución de equilibrio tiende a una distribución gamma asimétrica característica en forma de campana. En este modelo α = 1 / 3 . El retorno de cambio promedio fue 75 % .Algoritmo de intercambio proporcional: xs — n , m , alpha — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx j <- 0 n xs[j] <- xs[j] + dx
La disminución en la participación de los pobres se debe al hecho de que gastan en promedio menos de lo que reciben de los ricos, porque ambos intercambian acciones de su capital. Pero este ascensor social solo funciona cuandoα < 1 / 2 .
Si gasta más de la mitad de lo que tiene, la probabilidad de estar en los pobres se vuelve muy tangible. Para varios valoresSe puede obtener α muy diferente en forma de distribución con una amplia gama de injusticias:Diferentes opciones para distribuciones de equilibrio a costos proporcionales a la riqueza. Los gráficos están marcados con valores. α , y en el gráfico de la derecha entre paréntesis también están los valores del índice de Gini.Solución exacta, , . , , , , , , . , , , .
-
Gamma(k,θ) — , ,
k=1 . , . , — . —
, - , , -. ,
X∼Gamma(k1,θ),Y∼Gamma(k2,θ)⟹X+Y∼Gamma(k1+k2,θ)
, :
X∼Gamma(k,θ)⟹aX∼Gamma(k,aθ).
m α :
Gamma(1α−1,1m(1α−1)) .
Se puede ver que cuanto más se ve obligado a gastar la mayor parte de los actores del capital (por ejemplo, para las necesidades diarias o la alimentación), mayor es la proporción de pobres y menos justa se vuelve la sociedad. Curioso que conα = 1 / 2 equilibrio se convierte distribución exponencial, tanto en el modelo con un intercambio igual. La distribución exponencial es un caso especial de distribución gamma, por lo que esta transformación, en sí misma, no es sorprendente. Pero hay una sutileza curiosa: la entropía de este caso particular es más que la entropía de distribuciones con cualquier otro valorα .
Vea cómo cambia la entropía a medida que la situación se desarrolla α = 0,75 :
En el proceso de transición al equilibrio, el sistema "omite" el estado con la máxima entropía.Al principio, el valor de la entropía aumenta monotónicamente, luego, sin alcanzar un máximo teórico correspondiente a la distribución exponencial, se detiene y comienza a disminuir. ¿Existe una contradicción con la definición de un estado de equilibrio como un estado con un máximo de entropía? No hay contradicción, ya que el estado de equilibrio debe ser estacionario, es decir, no crea flujos de energía dirigidos y es estable o, hablando el lenguaje de la teoría de los sistemas dinámicos, atrae un sistema hacia sí mismo. Y de todo equilibrio estacionario será el estado con máxima entropía. Y en nuestro casoα = 0.75 , la distribución exponencial corresponde a un estado inestable.Investigadores de la Universidad de Boston Ispolatov y Krapivsky han complicado el modelo de intercambio proporcional de tal manera que el intercambio tiene en cuenta no solo el bienestar del gasto, sino también el de la recepción. Un millonario rara vez compra algo de una verdulería, y una verdulería rara vez tiene muchos ingresos, por otro lado, un fabricante de automóviles de clase extra solo interactuará con clientes adinerados, pero él mismo no será rentable. Y así, en los modelos en los que los ricos comienzan a pagar principalmente a los ricos y a los pobres, a los pobres, la sociedad se está desmoronando por completo., . α=0.3,β=0.1 (. ).-: xs — n , m , alpha — , , beta — , .
i <- 0 n xs[i] > 0 dx <- floor(xs[i]*alpha) xs[i] <- xs[i] - dx dx > 0 j <- 0 n d = min(dx, floor(xs[j]*beta)) xs[j] <- xs[j] + d dx <- dx - d
En este sistema, solo hay un estado estacionario: cuando todos los jugadores tienen (y por lo tanto no reciben) absolutamente nada, y toda la riqueza va a alguien solo. El coeficiente de Gini en este estado es casi igual a la unidad, y está muy lejos del equilibrio normal: su entropía es casi cero. La situación puede salvarse mediante una restricción desde abajo, que prohíbe a los jugadores perder absolutamente todos sus ahorros, en cuyo caso la distribución de equilibrio vuelve a ser exponencial o en forma de gamma. También podemos introducir una restricción desde arriba, luego obtenemos una cierta distribución asimétrica correspondiente a la distribución de Bernoulli. El modelo de un mercado tan salvaje es bastante aplicable al mercado de valores sin restricciones, pero están luchando con esto en los intercambios reales, introduciendo restricciones en el volumen de transacciones,comprometido por día y en niveles máximos de crecimiento o caída en el precio de un activo.Todas estas son conclusiones tristes, que no hablan a favor del libre mercado, o es el caso, el modelo propuesto por Sharikov. Pero, ¿cuál es la entropía de una distribución degenerada? Según la fórmula estándar, es exactamente cero. Esta es la distribución más desequilibrada, más improbable, y en cualquier modelo de intercambio es inestable, por lo que dicha sociedad solo puede obtenerse artificialmente. El mercado salvaje, por supuesto, no es un regalo: es inestable y tiende a deslumbrar la desigualdad. Se necesitan muchas restricciones mutuamente acordadas y relaciones afinadas para construir un mercado sostenible y una sociedad más o menos justa. La humanidad ha estado explorando este tema no por mucho tiempo y, básicamente, al tacto, por ensayo y error, pero una cosa está clara: la injusticia en el espacio económico no es una consecuencia de la naturaleza humana sucia, sino una propiedad objetiva del sistema.del cual todos somos parte. Además, los intentos de crear justicia absoluta en un estilo Sharikov siempre fueron con batalla y sangre, y los resultados, debido a su desequilibrio, no existieron por mucho tiempo.Es poco probable que las moléculas y los átomos estén hablando de la injusticia de su mundo, y los físicos e ingenieros durante doscientos años han llegado a un acuerdo con el hecho de que, sin importar qué motor térmico ideal construyeron, el caos no permitirá que el calor se convierta para funcionar más de lo que se requiere. Cuando está claro, no es tan ofensivo. Espero que este capítulo ayude a un lector curioso a comprender y aceptar nuestro mundo complejo e injusto.