Este texto está escrito para aquellos que estén interesados en el aprendizaje profundo, que quieran usar diferentes métodos de las bibliotecas pytorch y tensorflow para minimizar la función de muchas variables, que estén interesados en aprender cómo convertir un programa ejecutado secuencialmente en cálculos matriciales vectorizados realizados usando numpy. También puede aprender cómo hacer una caricatura a partir de datos visualizados usando PovRay y vapory.
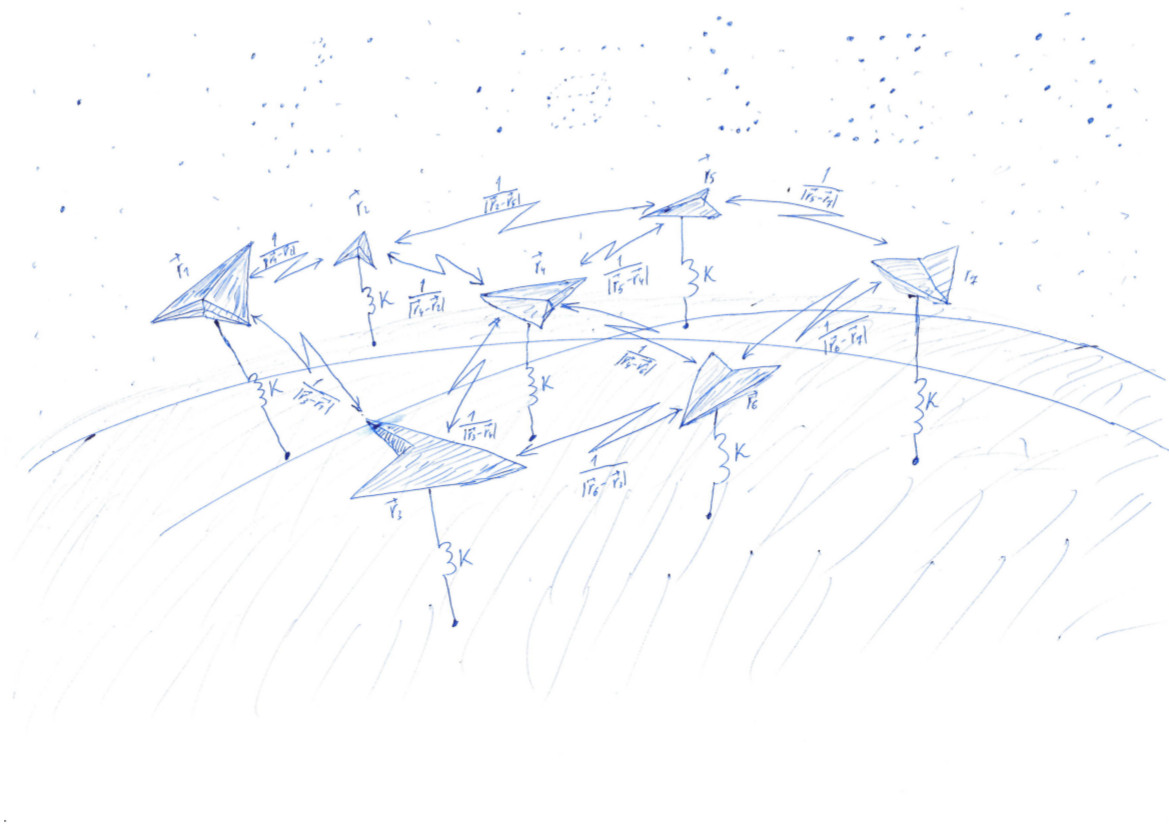
¿De dónde es la tarea?
Cada uno minimiza su funcionalidad (c) Científico de datos anónimos
En una de las publicaciones anteriores de nuestro blog , concretamente en el párrafo "Rake No. 6", hablamos sobre la tecnología DSSM, que le permite convertir texto en vectores. Para encontrar tal mapeo, uno necesita encontrar los coeficientes de las transformaciones lineales que minimizan la función de pérdida bastante compleja. Comprender lo que sucede cuando se aprende un modelo de este tipo es difícil debido a la gran dimensionalidad de los vectores. Para desarrollar una intuición que le permita elegir el método de optimización y establecer los parámetros de este método, puede considerar una versión simplificada de esta tarea. Ahora deje que los vectores estén en nuestro espacio tridimensional habitual, luego son fáciles de dibujar. Y la función de pérdida será el potencial de separar los puntos y atraer a la esfera de la unidad. En este caso, la solución al problema será una distribución uniforme de puntos sobre la esfera. La calidad de la solución actual es fácil de evaluar a simple vista.
Entonces, buscaremos una distribución uniforme sobre la esfera de una cantidad dada n puntos. Tal distribución es a veces necesaria para la acústica con el fin de comprender en qué dirección lanzar una onda en un cristal. Signalman: para descubrir cómo poner satélites en órbita para lograr comunicaciones de la mejor calidad. Meteorólogo: para la colocación de estaciones de monitoreo del clima.
Para algunos n La tarea se resuelve fácilmente . Por ejemplo, si n=8 , podemos tomar el cubo y sus vértices serán la respuesta al problema. También tenemos suerte si n será igual al número de vértices del icosaedro, dodecaedro u otro sólido platónico. De lo contrario, la tarea no es tan simple.
Para un número suficientemente grande de puntos, hay una fórmula con coeficientes seleccionados empíricamente , hay varias opciones más aquí , aquí , aquí y aquí . Pero hay una solución más universal, aunque más compleja, a la que se dedica este artículo.
Resolvemos un problema muy similar al problema de Thomson ( wiki ). Dispersión n puntos al azar, y luego haz que se atraigan a una superficie, como una esfera, y se alejen unos de otros. La atracción y la repulsión están determinadas por la función - potencial. En el valor mínimo de la función potencial, los puntos se ubicarán en la esfera de la manera más uniforme.
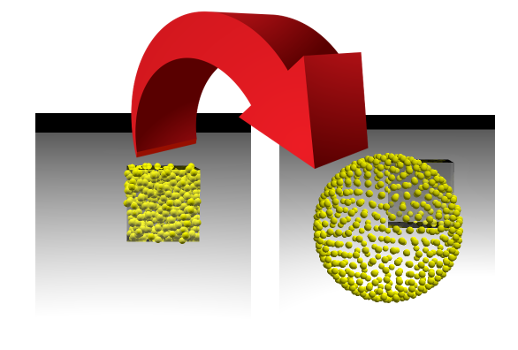
Esta tarea es muy similar al proceso de aprendizaje de los modelos de aprendizaje automático (ML), durante el cual se minimiza la función de pérdida. Pero un científico de datos generalmente observa cómo disminuye un solo número, y podemos ver cómo cambia la imagen. Si tenemos éxito, veremos cómo los puntos colocados aleatoriamente dentro del cubo con el lado 1 divergen a lo largo de la superficie de la esfera:
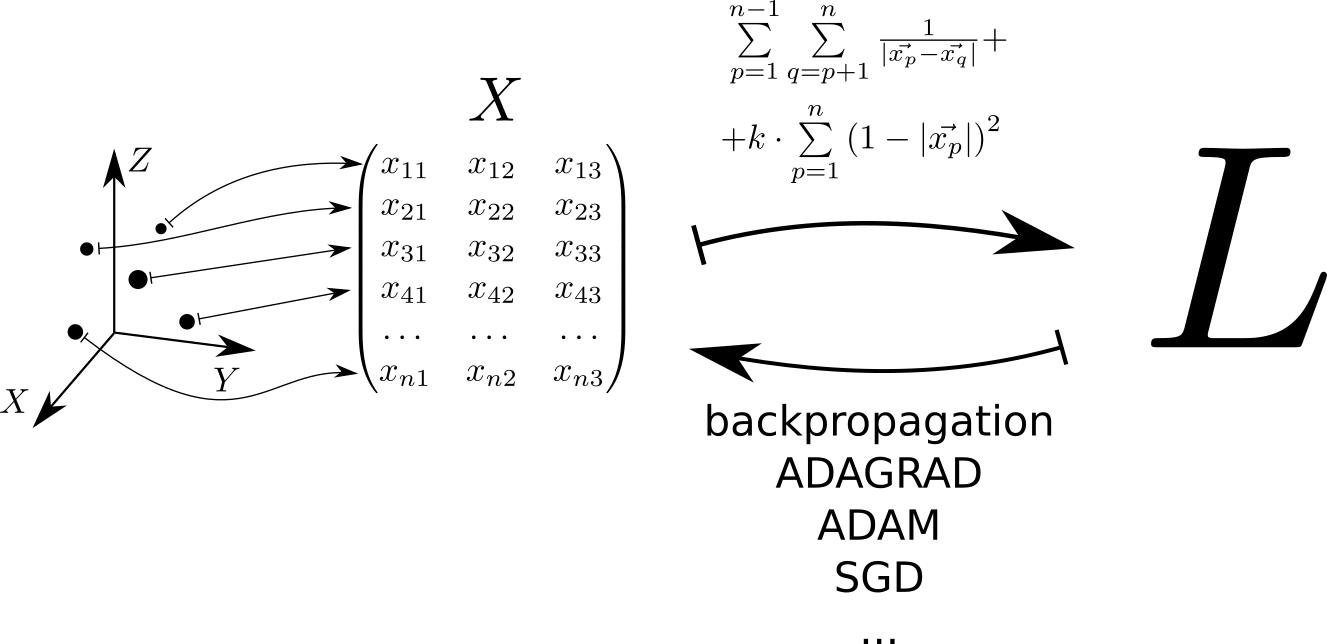
Esquemáticamente, el algoritmo para resolver el problema se puede representar de la siguiente manera. Cada punto ubicado en un espacio tridimensional corresponde a una fila de la matriz X . La función de pérdida se calcula a partir de esta matriz. L , cuyo valor mínimo corresponde a una distribución uniforme de puntos sobre la esfera. El valor mínimo se encuentra usando las tensorflow pytorch y tensorflow , que permiten calcular el gradiente de la función de pérdida por la matriz X y bajar al mínimo utilizando uno de los métodos implementados en la biblioteca: SGD, ADAM, ADAGRAD, etc.
Consideramos el potencial
Debido a su simplicidad, expresividad y capacidad para servir como interfaz para bibliotecas escritas en otros idiomas, Python es ampliamente utilizado para resolver problemas de aprendizaje automático. Por lo tanto, los ejemplos de código en este artículo están escritos en Python. Para cálculos rápidos de matriz, usaremos la biblioteca numpy. Para minimizar la función de muchas variables: pytorch y tensorflow.
Dispersamos al azar puntos en el cubo con el lado 1. Tengamos 500 puntos, y la interacción elástica es 1000 veces más significativa que la electrostática:
import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3)
Este código generó una matriz X el tamaño 3 vecesn lleno de números aleatorios del 0 al 1:
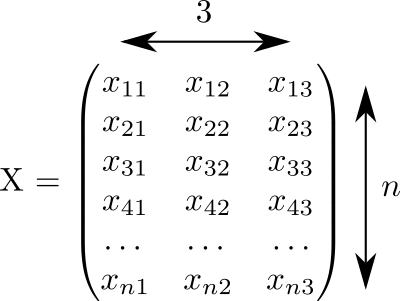
Suponemos que cada fila de esta matriz corresponde a un punto. Y en tres columnas se registran las coordenadas. x,y,z Todos nuestros puntos.
El potencial de interacción elástica de un punto con la superficie de una esfera unitaria. u1=k cdot(1−r)2/2 . Potencial de interacción electrostática de puntos p y q - u2=1/|rp−rq|$ . El potencial completo consiste en la interacción electrostática de todos los pares de puntos y la interacción elástica de cada punto con la superficie de la esfera:
U(x1,...,xn)= sum limitsn−1p=1 sum limitsnq=p+1 frac1 leftEl| vecxp− vecxq right|+k cdot sum limitsnp=1 left(1−| vecxp| right)2 rightarrow min
En principio, el valor potencial se puede calcular usando esta fórmula:
L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2
Pero hay un pequeño problema. Por unos patéticos 2000 puntos, este programa se ejecutará durante 2 segundos. Será mucho más rápido si calculamos este valor utilizando cálculos matriciales vectorizados. La aceleración se logra tanto mediante la implementación de operaciones matriciales utilizando los lenguajes "rápidos" fortran y C, como mediante el uso de operaciones de procesador vectorizadas que permiten realizar una acción sobre una gran cantidad de datos de entrada en un ciclo de reloj.
Veamos la matriz. S=X cdotXT . Tiene muchas propiedades interesantes y a menudo se encuentra en cálculos relacionados con la teoría de clasificadores lineales en ML. Entonces, si suponemos que en la fila de la matriz X con índices p y q los vectores espaciales tridimensionales se escriben vecrp, vecrq entonces la matriz S consistirá en productos escalares de estos vectores. Tales vectores n piezas, luego la dimensión de la matriz S es igual a n vecesn .
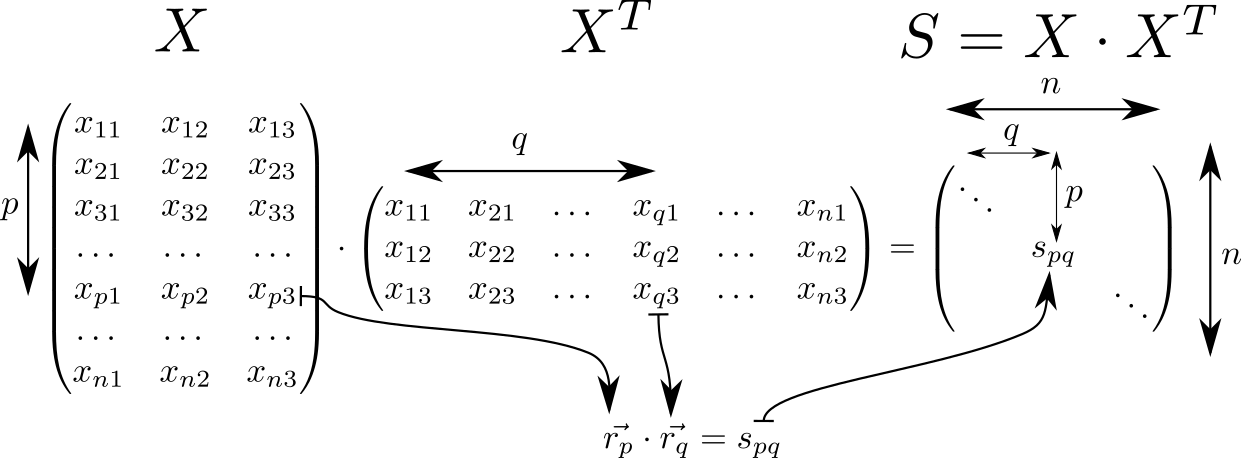
En la diagonal de la matriz S colocar cuadrados de longitudes de vectores vecrp:spp=r2p . Sabiendo esto, consideremos todo el potencial de interacción. Comenzamos calculando dos matrices auxiliares. En una matriz diagonal S se repetirá en filas, en otra, en columnas.
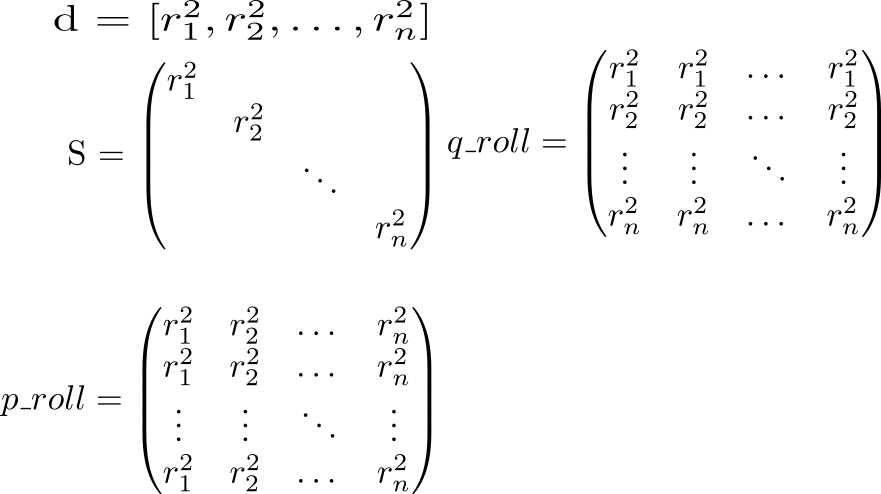
Ahora veamos el valor de la expresión p_roll + q_roll - 2 * S
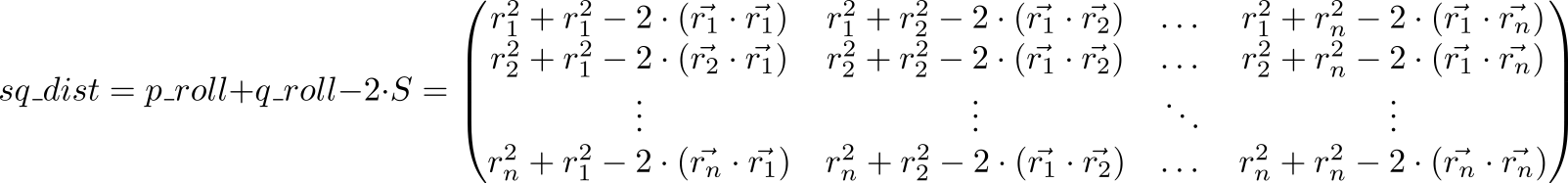
Artículo indexado (p,q) matriz sq_dist es igual r2p+r2q−2 cdot( vecrp, vecrq)=( vecrp− vecrq)2 . Es decir, tenemos una matriz de cuadrados de distancias entre puntos.
Repulsión electrostática en una esfera.
dist = np.sqrt(sq_dist) - matriz de distancias entre puntos. Necesitamos calcular el potencial, teniendo en cuenta la repulsión de puntos entre ellos y la atracción hacia la esfera. Coloque las unidades en diagonal y reemplace cada elemento con el inverso (¡no piense que invertimos la matriz!): rec_dist_one = 1 / (dist + np.eye(n)) . El resultado es una matriz en la diagonal de la cual hay unidades, otros elementos son los potenciales de la interacción electrostática entre los puntos.
Ahora agregamos el potencial cuadrático de atracción a la superficie de la esfera de la unidad. La distancia desde la superficie de la esfera. (1−r) . Ajústalo y multiplícalo por k , que define la relación entre el papel de la repulsión electrostática de partículas y la atracción de una esfera. Total k = 1000 , all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . La función de pérdida tan esperada, que minimizaremos: t = all_interactions.sum()
Un programa que calcula el potencial usando la biblioteca numpy:
S = X.dot(XT)
Aquí las cosas están un poco mejor: 200 ms en 2000 puntos.
Usamos pytorch:
import torch pt_x = torch.from_numpy(X)
Y finalmente tensorflow:
import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer()
Compare el rendimiento de estos tres enfoques:
| N | pitón | numpy | Pytorch | Tensorflow |
| 2000 | 4.03 | 0,083 | 1.11 | 0,205 |
| 10,000 | 99 | 2,82 | 2,18 | 7,9 |
Los cálculos vectorizados dan una ganancia de más de un orden decimal y medio en relación con el código de Python puro. La "placa de la caldera" en pytorch es visible: los cálculos de volúmenes pequeños toman una cantidad de tiempo notable, pero casi no cambian con el aumento del volumen de los cálculos.
Visualización
Hoy en día, los datos se pueden visualizar utilizando una gran cantidad de paquetes, como Matlab, Wolfram Mathematica, Maple, Matplotlib, etc., etc. En estos paquetes hay muchas funciones complejas que hacen cosas complejas. Desafortunadamente, si te enfrentas a una tarea simple pero no estándar, te encuentras desarmado. Mi solución favorita en esta situación es povray. Este es un programa muy poderoso que generalmente se usa para crear imágenes fotorrealistas, pero se puede usar como un "ensamblador de visualización". Por lo general, no importa cuán difícil sea la superficie que desea mostrar, solo pídale a povray que dibuje esferas con centros en esa superficie.
Usando la biblioteca de vapor, puede crear una escena povray directamente en python, renderizarla y ver el resultado. Ahora se ve así:

La imagen se obtiene de la siguiente manera:
import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm))
A partir de un montón de archivos, los gifs animados se ensamblan usando ImageMagic:
convert -delay 10 -loop 0 sphere_*.png sphere_all.gif
En github puedes ver el código de trabajo, cuyos fragmentos se dan aquí. En el segundo artículo, hablaré sobre cómo comenzar a minimizar lo funcional para que los puntos salgan del cubo y se distribuyan uniformemente por la esfera.