Hay una serie de tareas en las que el rango de valores de salida debe ser limitado, mientras que los datos de entrada no pueden garantizarlo. Además de las situaciones forzadas, la limitación de la señal puede ser una tarea orientada a objetivos, por ejemplo, al comprimir una señal o implementar el efecto de "sobremarcha".
La implementación más simple de una restricción es forzarla a un cierto valor si se excede un cierto nivel. Por ejemplo, para una sinusoide con amplitud creciente, se verá así:

Aquí, la función Clip actúa como un limitador, como un argumento del cual se transmiten la señal de entrada y los parámetros de restricción, y el resultado de la función es la señal de salida.
Veamos el gráfico de la función de clip por separado:
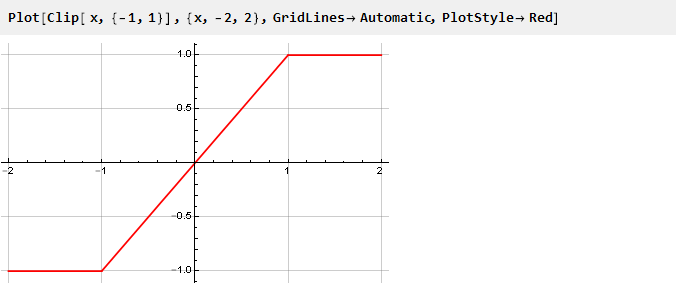
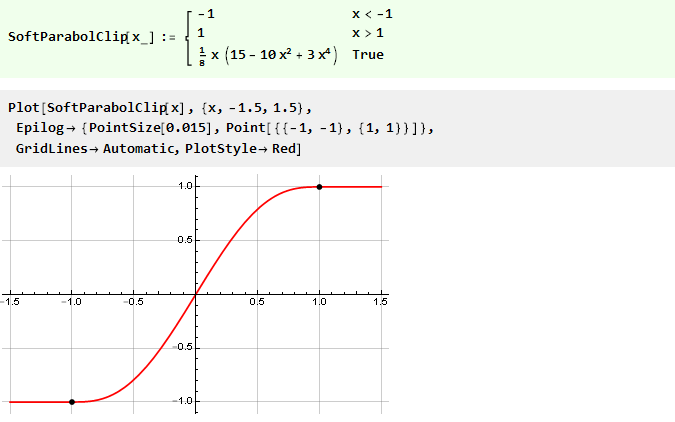
Se puede ver de él que, si bien no excedemos los límites del límite, el valor de salida es igual a la entrada y la señal no cambia; cuando se excede, el valor de salida no depende de la entrada de ninguna manera y permanece en el mismo nivel. De hecho, tenemos una función continua por partes compuesta de otras tres: y = -1, y = x e y = 1, seleccionadas según el argumento, y equivalentes a la siguiente notación:

La transición entre funciones ocurre de manera bastante abrupta; y se ve tentador para hacerlo más suave. Matemáticamente, esta nitidez se debe al hecho de que las derivadas de las funciones en los puntos de acoplamiento no coinciden. Esto es fácil de ver al trazar la derivada de la función Clip:
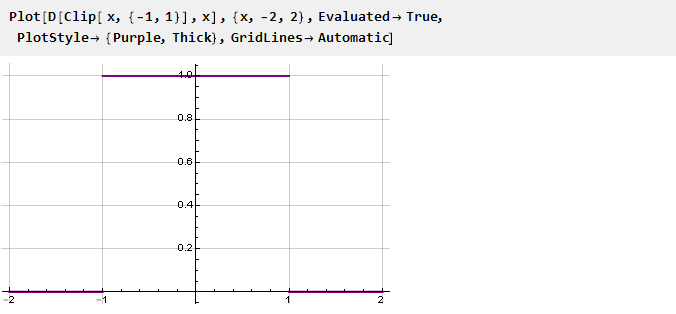
Por lo tanto, para garantizar la suavidad de la función de restricción, es necesario garantizar la igualdad de los derivados en los puntos de unión. Y dado que las funciones extremas que tenemos son constantes, cuyas derivadas son iguales a cero, entonces las funciones de restricción derivadas en los puntos de acoplamiento también deben ser iguales a cero. A continuación, consideraremos varias de estas funciones que garantizan un acoplamiento sin problemas.
Seno
Lo más simple es usar la función sin en el intervalo de -pi / 2 a pi / 2, en cuyos bordes los valores de la derivada son iguales a cero por definición:
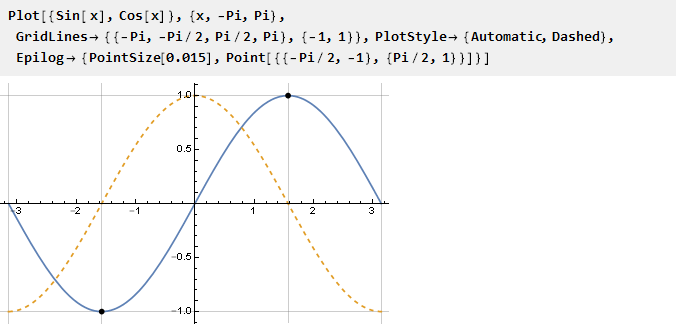
Solo necesita escalar los argumentos para que la unidad se proyecte en el Pi / 2. Ahora podemos definir la propia función delimitadora:

Y construye su horario:
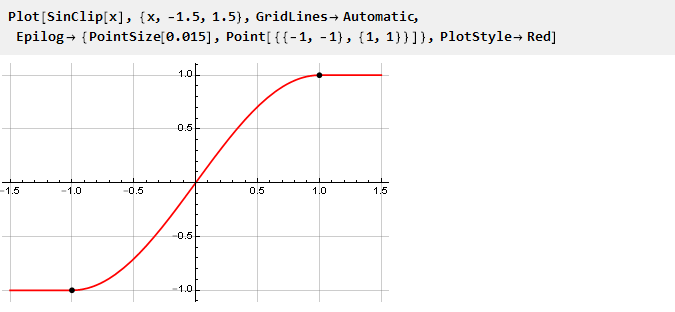
Dado que los límites de nuestra restricción están estrictamente definidos, la restricción se establece al escalar la señal de entrada con una escala posterior (si es necesario).
Tampoco existe una situación en la que la señal de entrada se transmite a la salida sin distorsión (cuanto menor es el nivel de ganancia, menor es el nivel de distorsión debido a la limitación), pero la señal se distorsiona en cualquier caso.
El efecto del parámetro de ganancia en la distorsión de la señal también se puede ver en la dinámica:

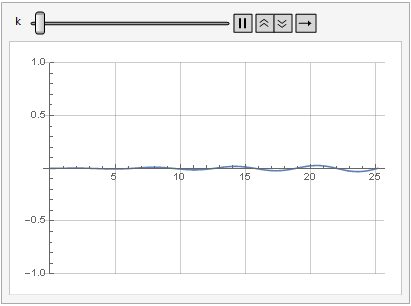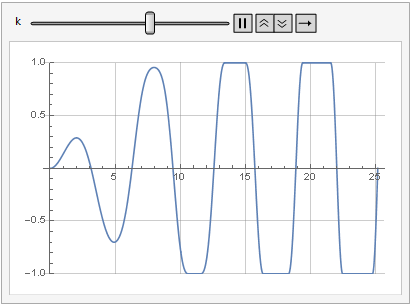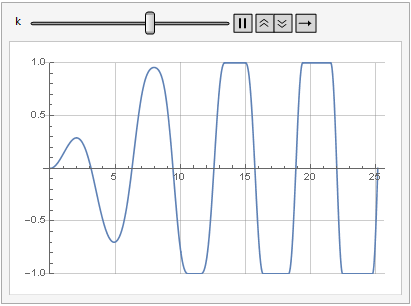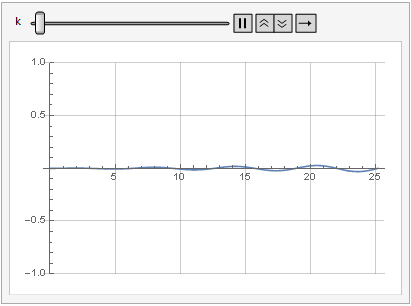
Más suavidad
Veamos la derivada de nuestra función:
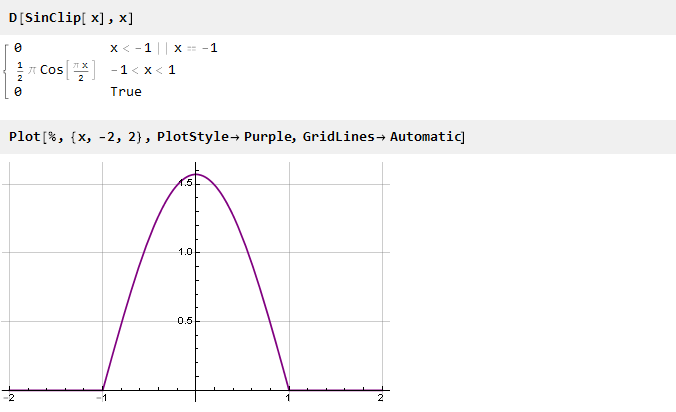
Ya no tiene huecos en los valores, pero hay huecos en la derivada (el segundo, si contamos desde la función original). Para eliminarlo, puede ir en sentido contrario: primero forme una derivada suave y luego integre para obtener la función deseada.
La forma más fácil de anular la derivada en los puntos -1 y 1 es simplemente cuadrar la función: todos los valores negativos de la función se volverán positivos y, en consecuencia, se producirán inflexiones en los puntos de intersección de la función con cero.
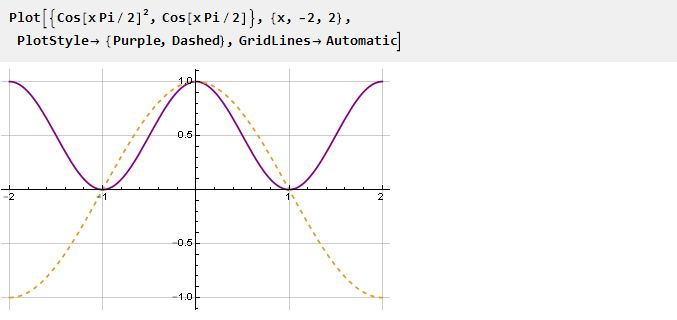
Encuentra la antiderivada:
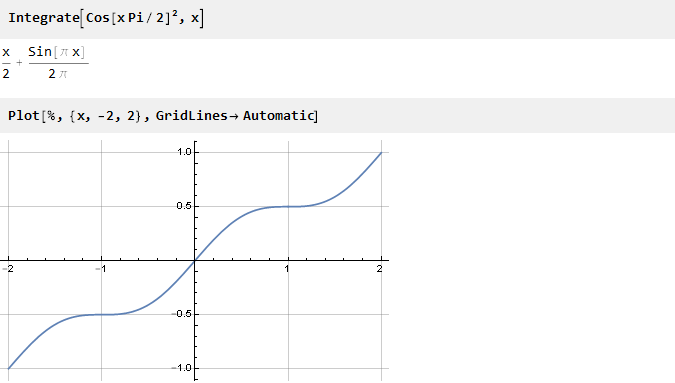
Ahora queda escalarlo a lo largo del eje de ordenadas. Para hacer esto, encuentre su valor en el punto 1:

Y dividir por él (sí, específicamente aquí es una multiplicación elemental por 2, pero esto no siempre sucede):

Por lo tanto, la función de restricción final tomará la forma:
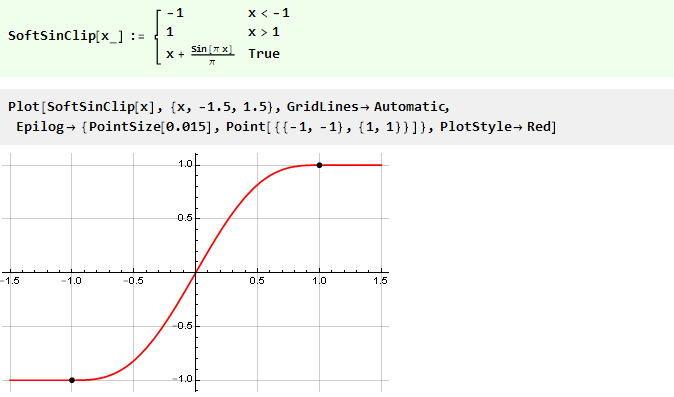
Pasamos a polinomios
El uso de funciones trigonométricas en algunos casos puede ser algo inútil. Por lo tanto, trataremos de construir la función que necesitamos, permaneciendo dentro del marco de operaciones matemáticas elementales.
Considere la parábola:
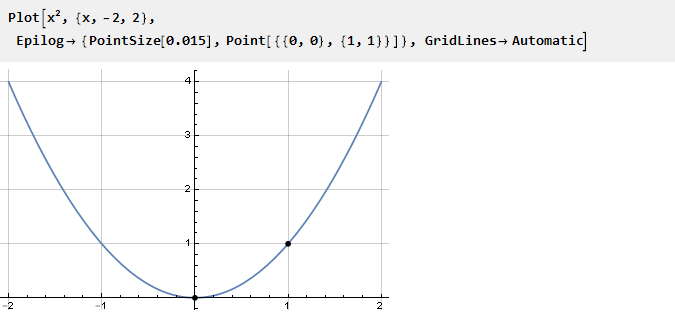
Como ya tiene una inflexión en el punto cero, podemos usar la misma parte en el intervalo {0,1} para acoplar con constantes. Para valores negativos, debe desplazarse hacia abajo y hacia la izquierda:

y para positivo: refleje vertical y horizontalmente:

Y nuestra función con una parábola tomará la forma:
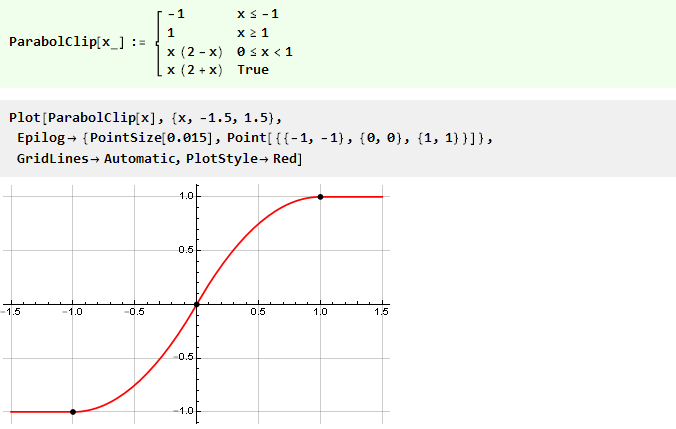
Vamos a complicarnos un poco
Volvamos a nuestra parábola, déle la vuelta y suba una unidad:
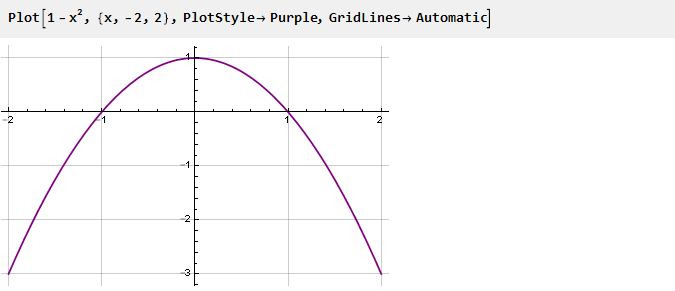
Esto será un derivado de nuestra función. Para hacerlo más suave en los puntos de unión, ajustaremos al cuadrado, poniendo a cero la segunda derivada de esta manera:
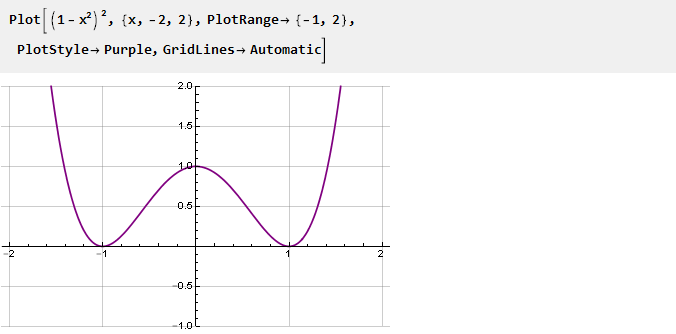
Integrar y escalar:

Obtenemos una función aún más suave:
Más suavidad para el dios de la suavidad.
Aquí tratamos de lograr suavidad en los puntos de acoplamiento en derivados aún más altos. Para hacer esto, para empezar, definimos la función como un polinomio con coeficientes desconocidos, y tratamos de encontrar los coeficientes a través de una solución del sistema de ecuaciones.
Comencemos con la primera derivada:

2do:

3er:

Todos estos coeficientes parecen tener algún tipo de lógica. Escribimos los factores, multiplicándolos por el valor del grado en x; y para no escribir lo mismo cada vez, automatizamos el proceso de encontrar los coeficientes:

Parecen coeficientes binomiales. Asumimos audazmente que lo son y, sobre la base de esto, escribimos la fórmula generalizada:

Comprobar:
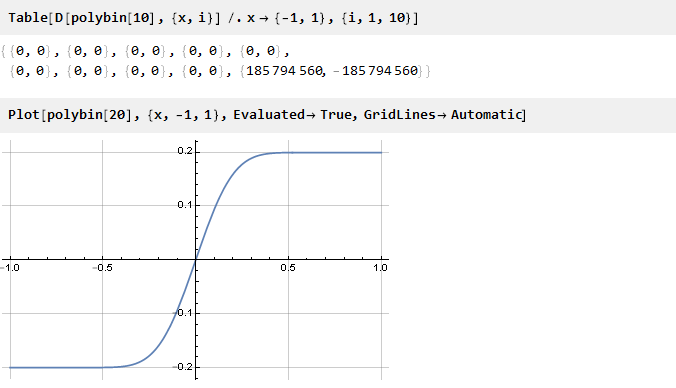
Parece ser cierto
[1] . Solo queda calcular el factor de escala para unir los bordes:

Y después de la escala y la simplificación, encontramos que nuestro conocimiento de las matemáticas está algo desactualizado
[2] :
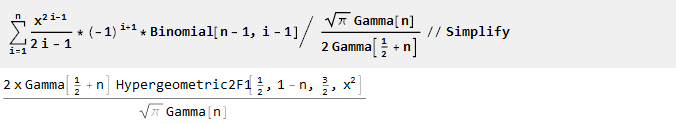
Por lo tanto, hemos obtenido una función generadora de orden n en la que n-1 de las primeras derivadas son iguales a cero:

Veamos que pasó:
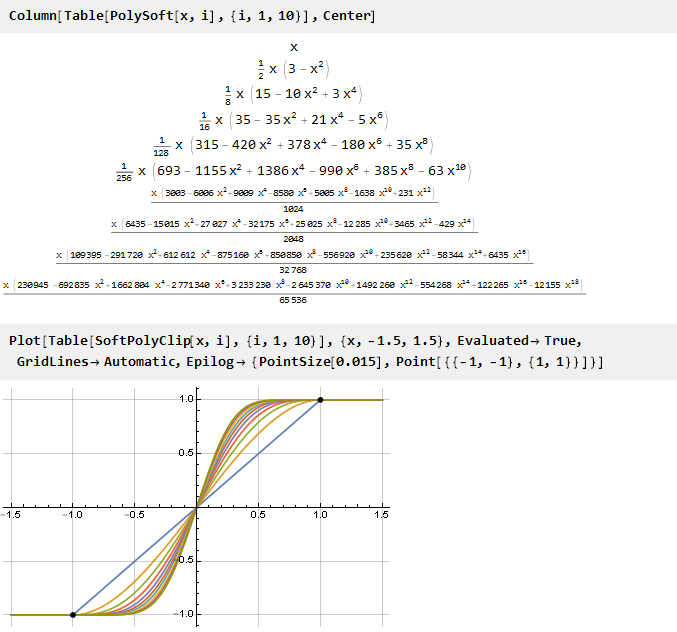
Y dado que nuestra fórmula generalizada resultó ser continua, puede usar valores de parámetros no enteros si lo desea:
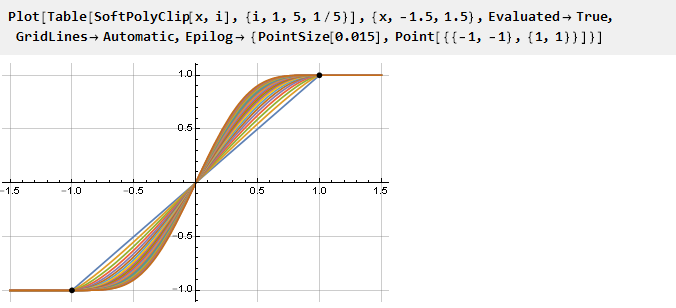
También puede crear gráficos de derivados reducidos a una escala:
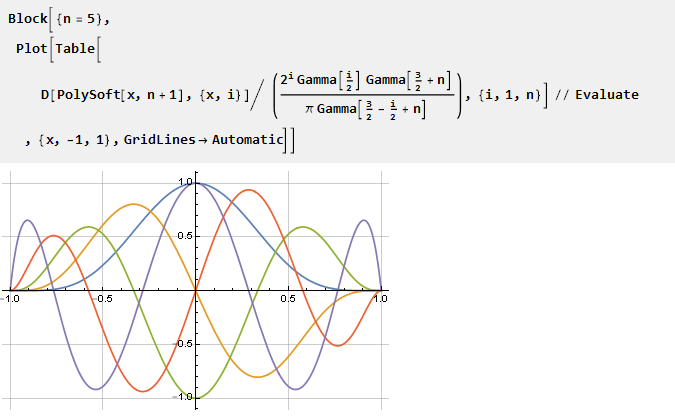
Añadir rigidez
Sería tentador poder ajustar el grado de "rigidez" de la restricción.
Volvamos a nuestra parábola invertida y agreguemos un coeficiente en el grado x:

Cuanto mayor sea n, mayor será nuestra derivada "cuadrada", y su antiderivada es aguda, respectivamente:
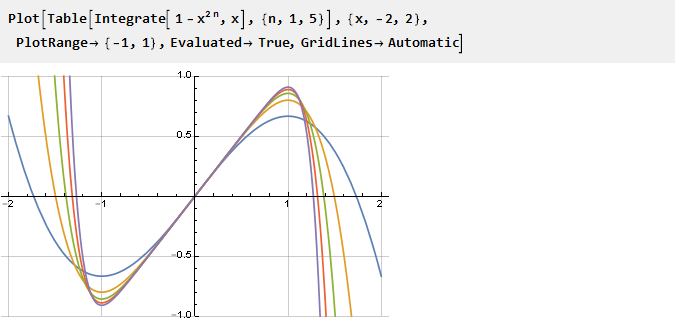
Calculamos la antiderivada y ajustamos la escala:

Ahora intentemos establecer el paso fraccional para el parámetro:
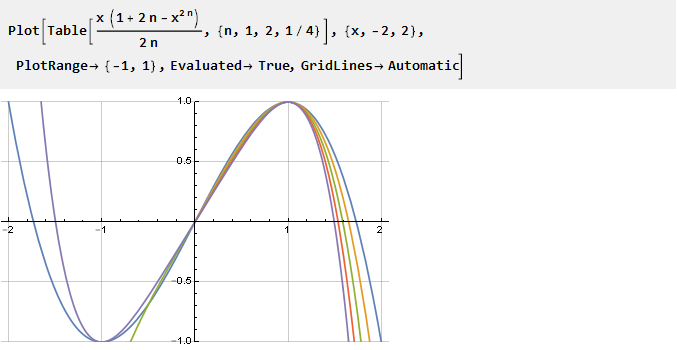
Como puede ver, no todos los n tienen la solución correcta en la parte negativa, pero las condiciones necesarias para nosotros aún se cumplen en la parte correcta (positiva), por lo tanto, para valores negativos, simplemente podemos usarlo invertido con un argumento inverso. Y dado que el dominio de definición del parámetro ya no se limita solo a enteros positivos, podemos simplificar la fórmula reemplazando 2n por n:

Y reemplazando n con n-1, puede hacer que la fórmula sea un poco más hermosa:
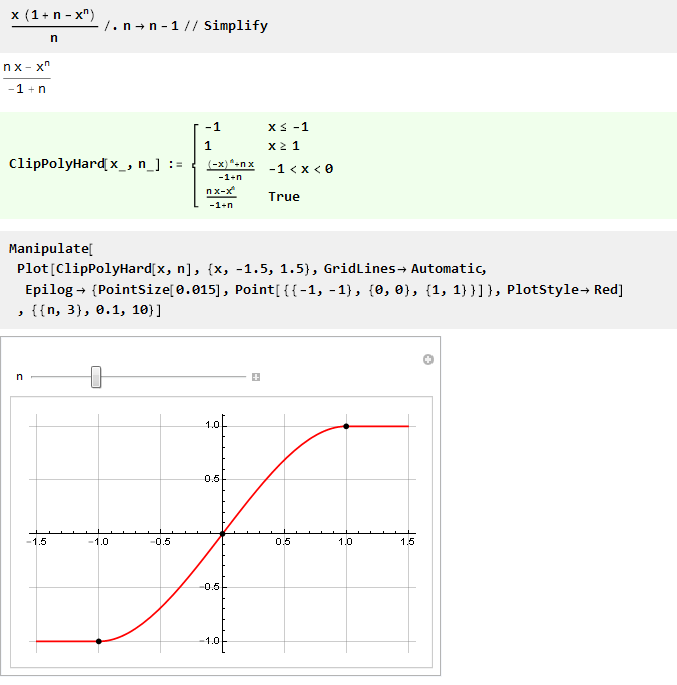
Como para n igual a uno obtenemos división por cero, luego tratamos de encontrar el límite:

Se encuentra el límite, lo que significa que ahora podemos agregar
[3] la función para n a 1 y considerarla para todos los n ceros grandes:
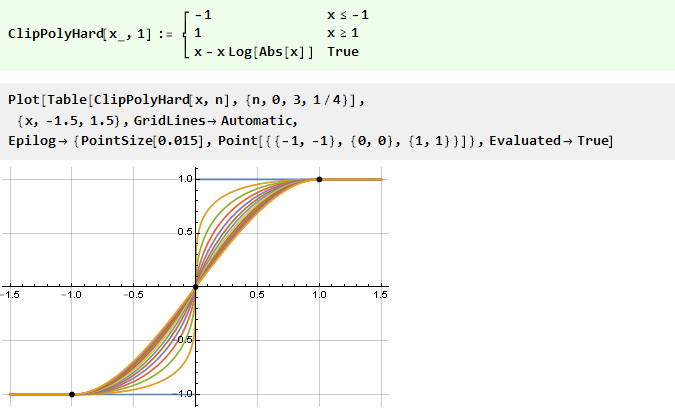
Si inicialmente cuadramos nuestra parábola invertida, obtenemos una función aún más suave:
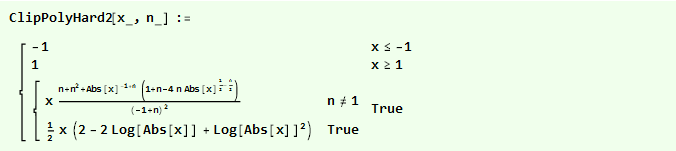
Y podemos compararlos en un gráfico:
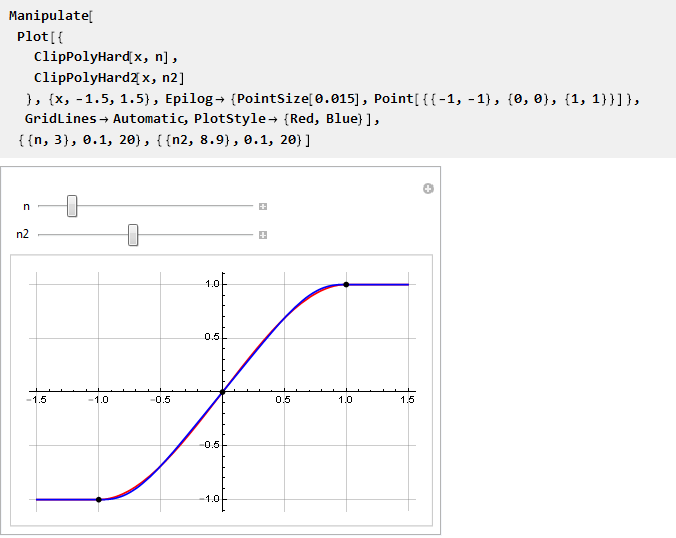
Agilizarlo
Veamos la siguiente función:
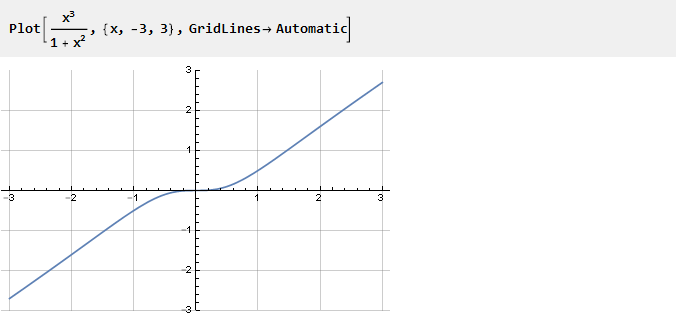
Ella no apareció por casualidad.
Si quitas una unidad, x
2 se contraerá y solo quedará x, es decir, una línea inclinada. Por lo tanto, cuanto menor es el valor de x, mayor es la influencia de la unidad en el denominador, creando la curvatura que necesitamos. Y teniendo en cuenta esta función a diferentes escalas, puede controlar el grado de esta curvatura:

Por lo tanto, podemos reescribir la función anterior con control de rigidez usando solo un polinomio racional de 3 órdenes:
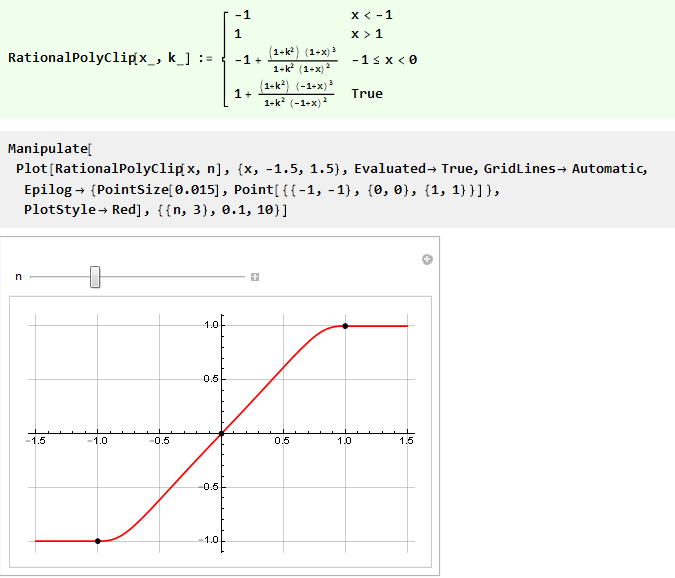
Automatizarlo
Para no especificar funciones continuas por partes cada vez, podemos definir una función auxiliar que lo haga por sí sola, tomando una función donante como argumento como entrada.
Si nuestra función ya tiene simetría diagonal y está alineada con el centro de coordenadas (como una onda sinusoidal), entonces simplemente podemos hacer
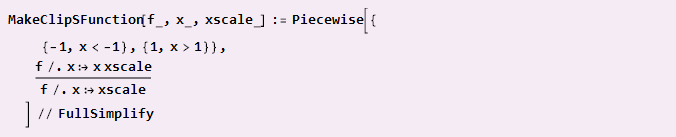
Ejemplo de uso:

Si necesita ensamblar a partir de piezas, como en el caso de una parábola, y el centro de coordenadas determina los puntos de acoplamiento, la fórmula será un poco más complicada:
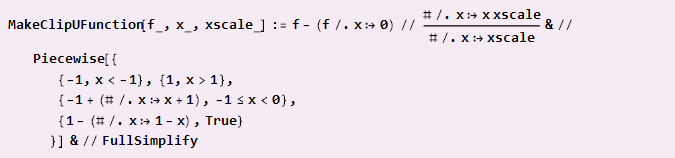
Ejemplo de uso:

Pasemos al expositor
Absolutamente cualquier función puede ser un donante para resolver este problema, solo necesita proporcionarle puntos de inflexión. Tomemos, por ejemplo, el exponente desplazado hacia abajo por uno:
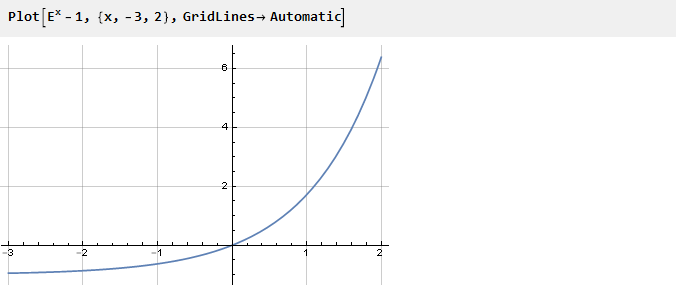
Anteriormente, para garantizar la inflexión necesaria en el punto cero, ajustamos la función al cuadrado. Pero puede ir hacia otro lado; por ejemplo, resuma con otra función cuya derivada en el punto cero sea opuesta en signo a la derivada del exponente. Por ejemplo, -x:
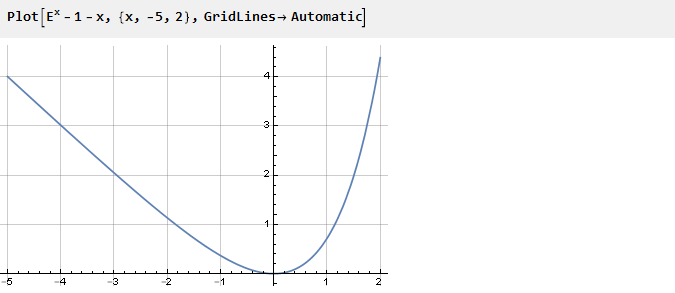
Dependiendo de qué lado tomaremos la curva, la forma final de la función dependerá de ella. Ahora, usando la función auxiliar previamente definida y eligiendo uno de los lados, obtenemos:

Ya sea

Y ahora podemos compararlos en un gráfico:
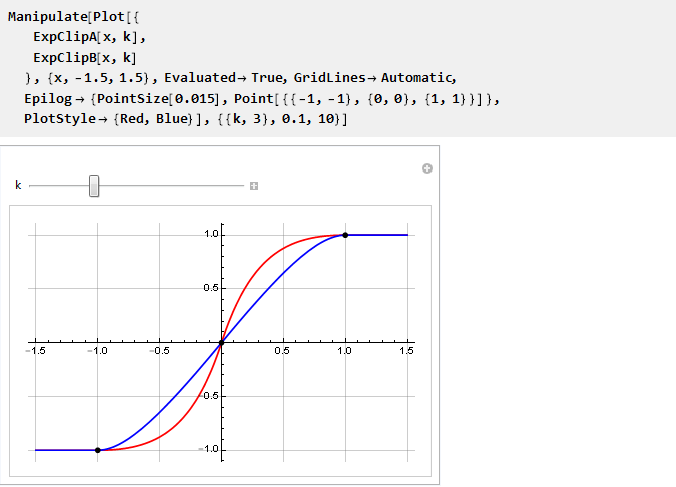
Se ve que como k → 0 tienden a coincidir; y dado que no podemos calcular directamente sus valores, ya que obtenemos división por cero, usaremos el límite:

Y obtuvieron la función por partes de la parábola que ya conocemos.
Rompiendo la simetría
Hasta ahora, hemos estado considerando funciones exclusivamente simétricas. Sin embargo, hay momentos en que no necesitamos simetría, por ejemplo, para simular distorsiones en el sonido de los amplificadores de válvulas.
Tome el exponente y multiplíquelo por la parábola invertida al cuadrado - para obtener la intersección con el eje de abscisas en los puntos -1 y 1, y al mismo tiempo asegurar la suavidad de la segunda derivada; La parametrización es posible mediante la escala del argumento exponente:
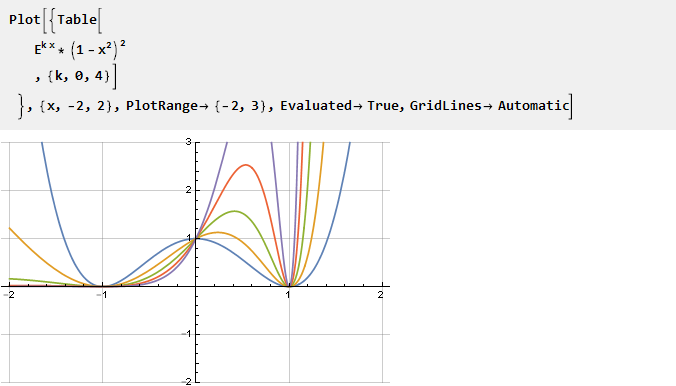
Encuentre la antiderivada y escale:
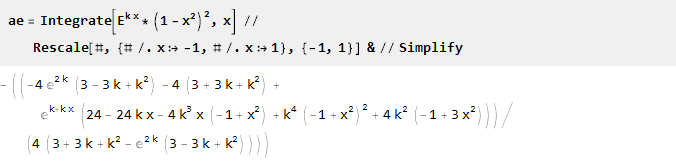
Como para k = 0 obtenemos la división por cero:

Luego, además, encontramos el límite,

que es un polinomio suave del tercer orden que ya conocemos. Combinando todo en una función, obtenemos
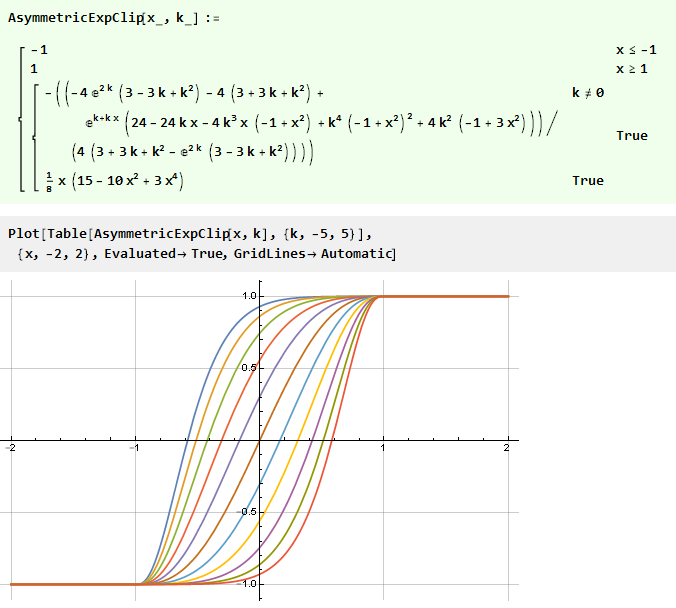
En lugar de diseñar inicialmente una función asimétrica, puede ir hacia otro lado: use la simétrica ya preparada, pero “doble” el valor de esta función usando una función de curva adicional definida en el intervalo {-1,1}.
Considere, por ejemplo, una hipérbola:
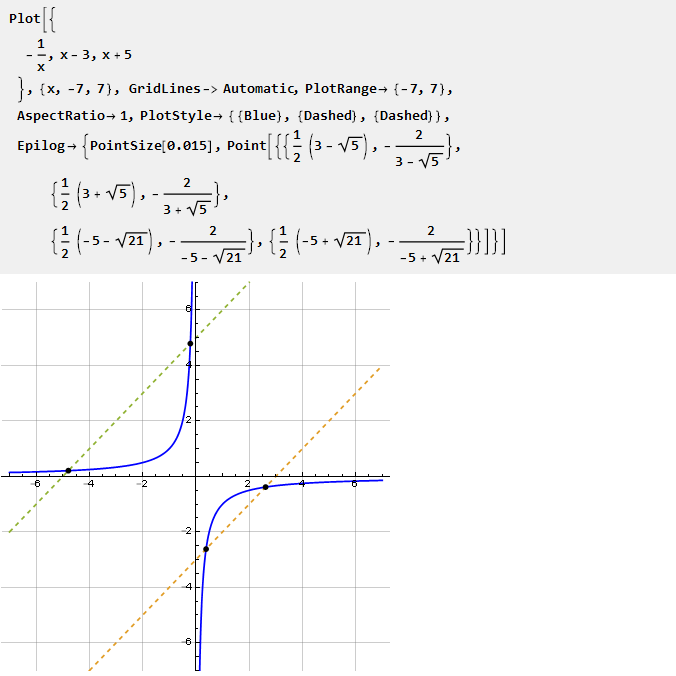
Teniendo en cuenta su segmento a diferentes escalas, puede ajustar el grado de curvatura en ambas direcciones. ¿Cómo encontrar este segmento? Según el gráfico, se podría buscar la intersección de la hipérbola con la línea. Sin embargo, dado que tal intersección no siempre existe, esto crea algunas dificultades. Por lo tanto, iremos por el otro lado.
Primero, agregue factores de escala a la hipérbola:

luego compondremos un sistema de ecuaciones que definan las condiciones para el paso de una hipérbola a través de puntos dados, y su solución nos dará los coeficientes que nos interesan:

Ahora sustituya la solución en la fórmula original y simplifique:

Veamos qué obtenemos, dependiendo del parámetro k:
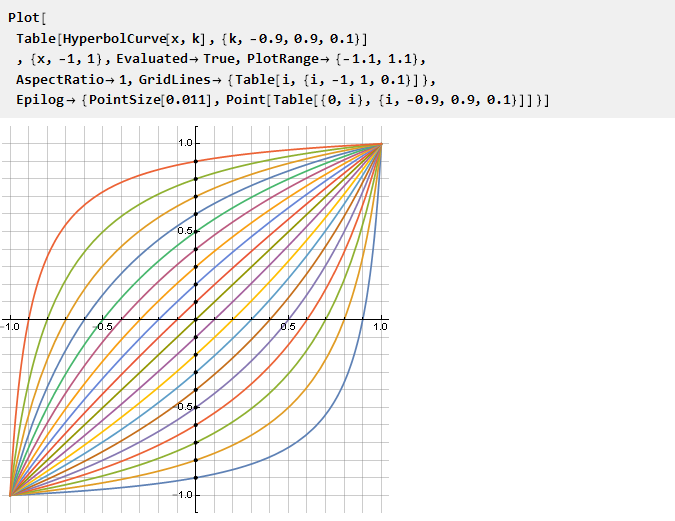
Es digno de mención que en k = 0 la fórmula colapsa naturalmente en x y no ocurren situaciones especiales, aunque con referencia a la hipérbole inicial esto es equivalente a un segmento de longitud cero y dos a la vez. No es menos notable que la función inversa a ella sea la misma, pero con un parámetro negativo k:

Ahora podemos usarlo para modificar una función de restricción arbitraria, y el parámetro k establece el punto de intersección con el eje de ordenadas:
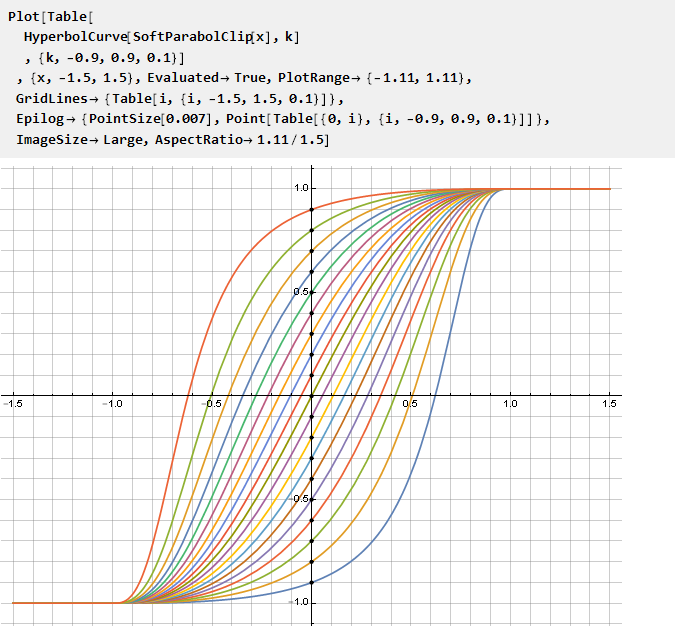
Del mismo modo, puede crear curvas a partir de otras funciones, por ejemplo, una ley de potencia con una base variable:
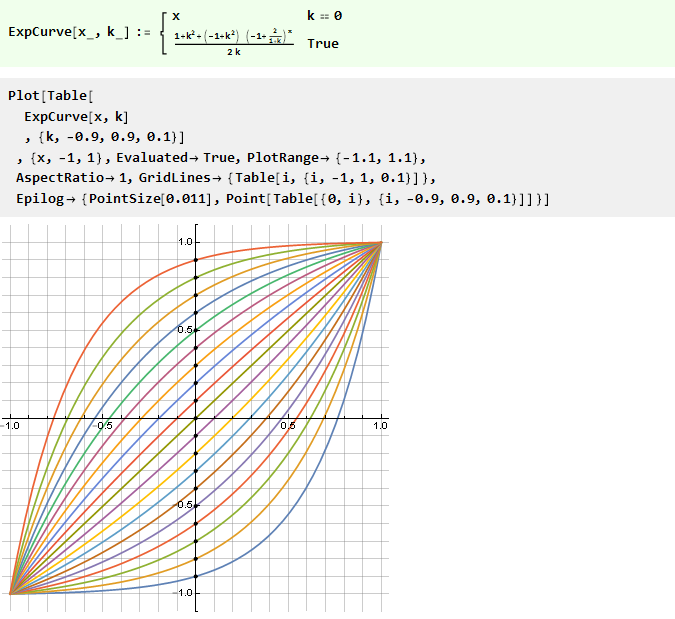
O lo contrario es logarítmico:
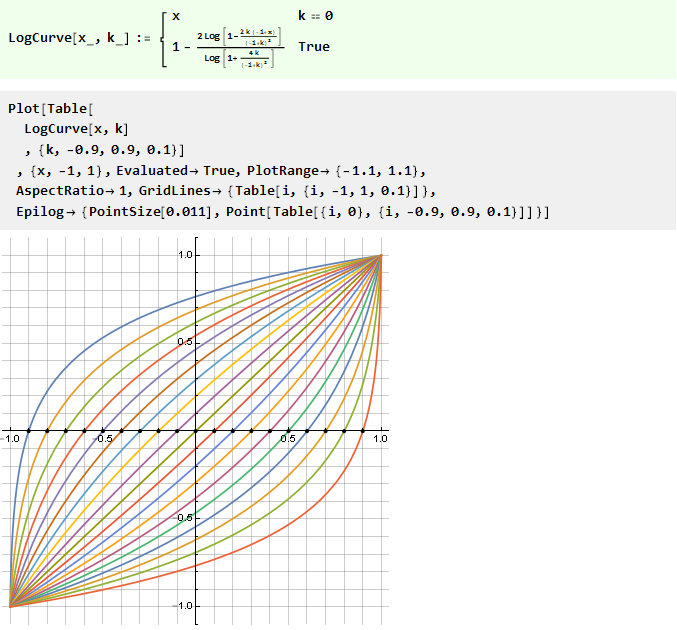
Necesita más precisión
Es posible que deseemos tener un espacio lineal garantizado para una función en un intervalo determinado. Esto es lógico de organizar mediante la introducción de una línea recta en una función continua por partes,
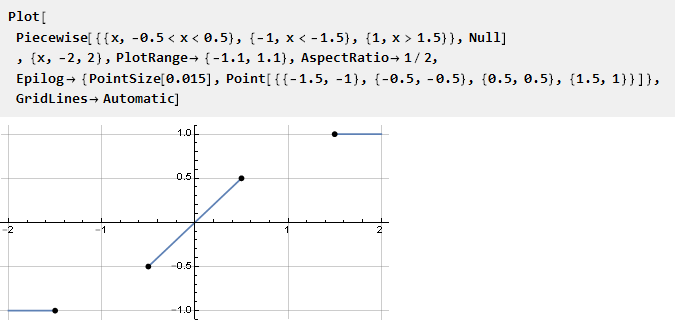
espacios vacíos en los que necesita completar alguna función. Obviamente, para un acoplamiento suave con una sección lineal, su primera derivada debe ser igual a la unidad; y todo posterior (si es posible) cero. Para no volver a deducir dicha función, podemos tomar una ya preparada y adaptarla para esta tarea. También puede notar que los puntos extremos están ubicados un poco más allá de la unidad, esto es necesario para mantener la pendiente de la sección lineal.
Tome la función PolySoft previamente derivada y desplace para que obtengamos una en el centro de coordenadas:
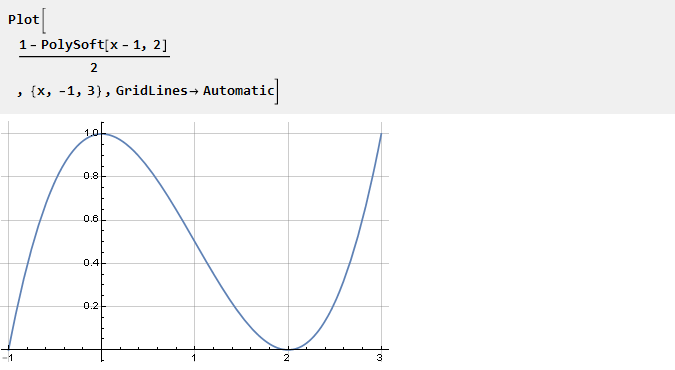
De sus propiedades se deduce que n-1 de las derivadas posteriores en los puntos 0 y 2 será igual a cero:
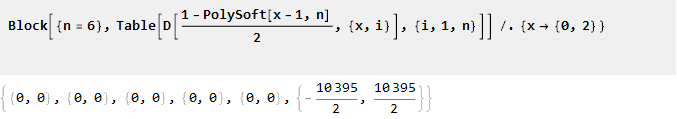
Ahora integrelo:
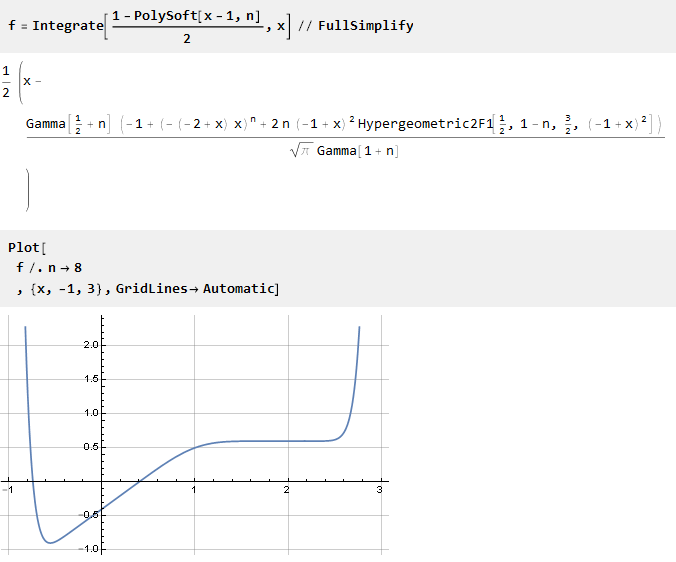
La función se desplazó hacia abajo en relación con el eje de abscisas. Por lo tanto, es necesario agregar una constante (igual al valor de la función en el punto 0) para combinar los centros de coordenadas:

Aquí tenemos cero en grado n. No ha disminuido, ya que el valor de cero en el grado de cero no está definido; podemos eliminarlo manualmente o, en simplificación, podemos indicar explícitamente que n es mayor que cero:

Lo comprobaremos por si acaso. El valor en los puntos 0 y 2 para todos n:

Derivados en los bordes del intervalo (para un polinomio de orden 5):

Como puede ver, la función resultó ser bastante engorrosa. Para no arrastrarlo y no complicar los cálculos, continuaremos manipulando con un polinomio específico, por ejemplo, cuarto orden:

Y ahora con él puedes llenar el espacio libre:

Comprobar:
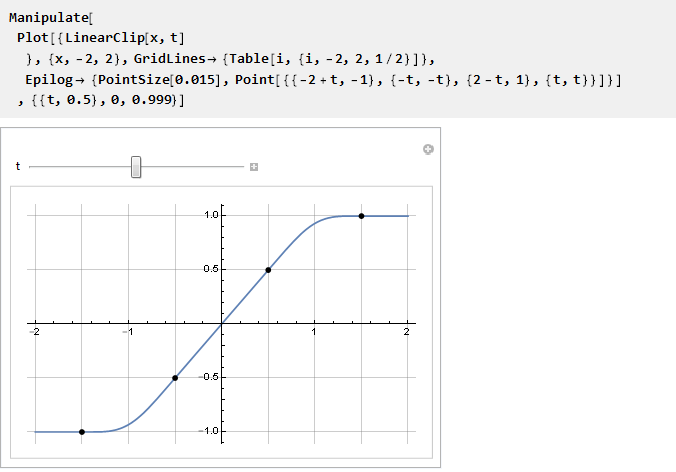
Vamos al infinito
A veces puede haber una necesidad de funciones que tienden a una unidad pero que no la alcanzan. Wikipedia
sugiere varias soluciones bien conocidas:
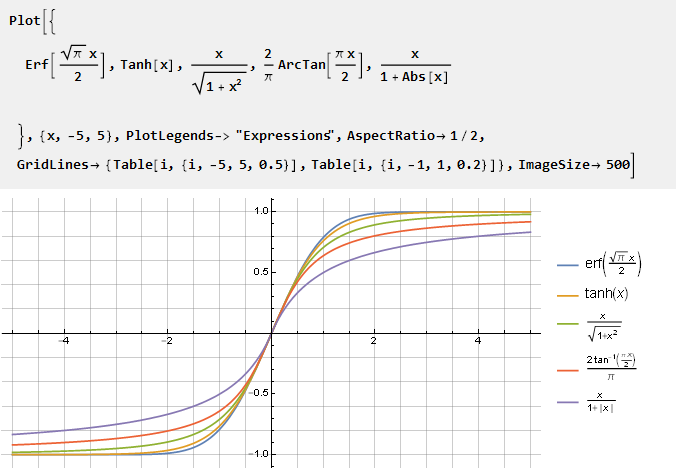
Como estas funciones no alcanzan la unidad, es más conveniente normalizarlas con respecto a la derivada en el centro de coordenadas.
Podemos modificar la forma de tales funciones a través de su argumento usando alguna función simétrica diagonal, por ejemplo:
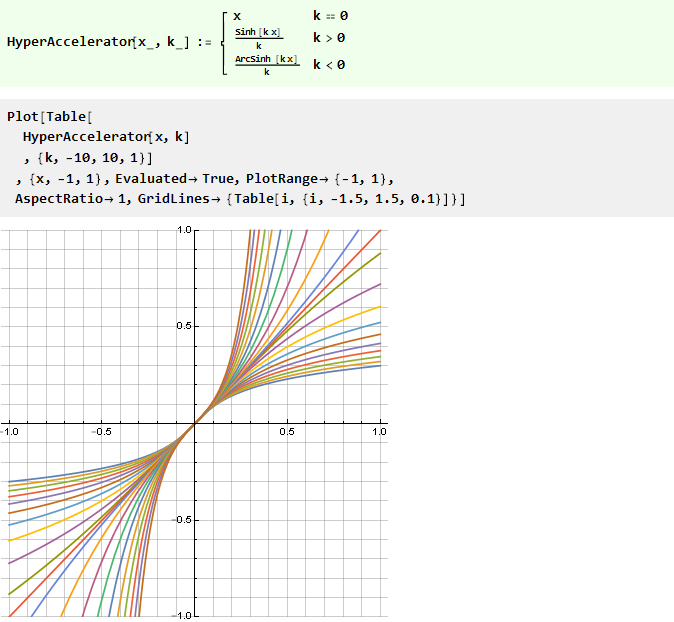
Esta función, por cierto, también es inversa a sí misma, es decir
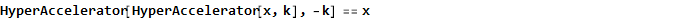
Y, como se aplica a arctangent, como ejemplo, obtenemos
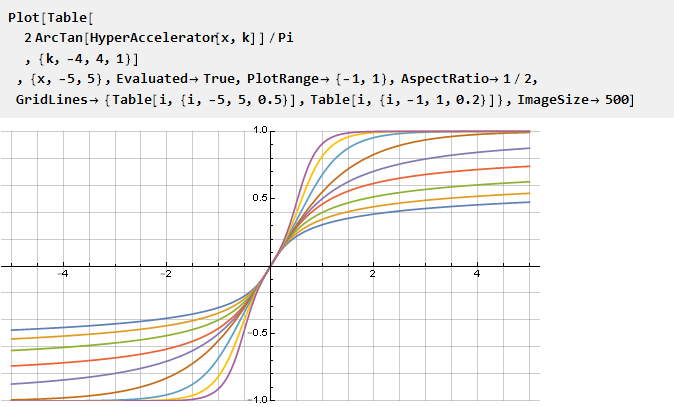
que, en particular, con el parámetro k = 1 nos dará
la función Guderman .
Como puede ver, con este enfoque, se pueden obtener torceduras indeseables, por lo tanto, es más preferible controlar la rigidez de la restricción directamente a través de la propiedad de la función misma. Considere varias de esas funciones con un parámetro, cuya salida se omite por brevedad.
Desde la función de potencia:
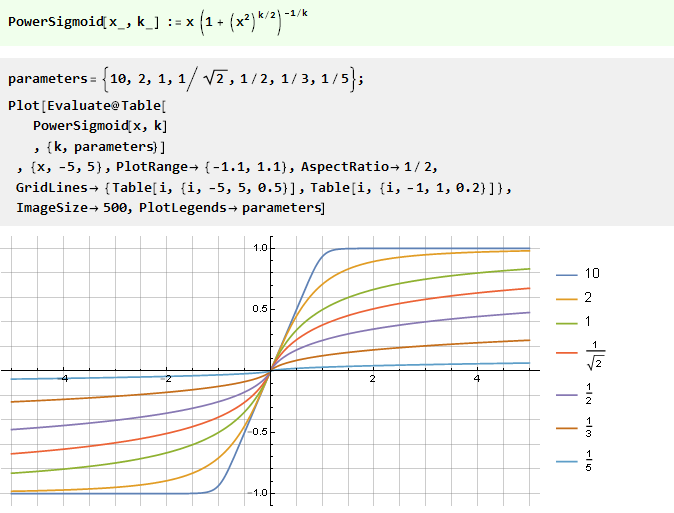
De la suma de dos funciones en forma de V con un desplazamiento:
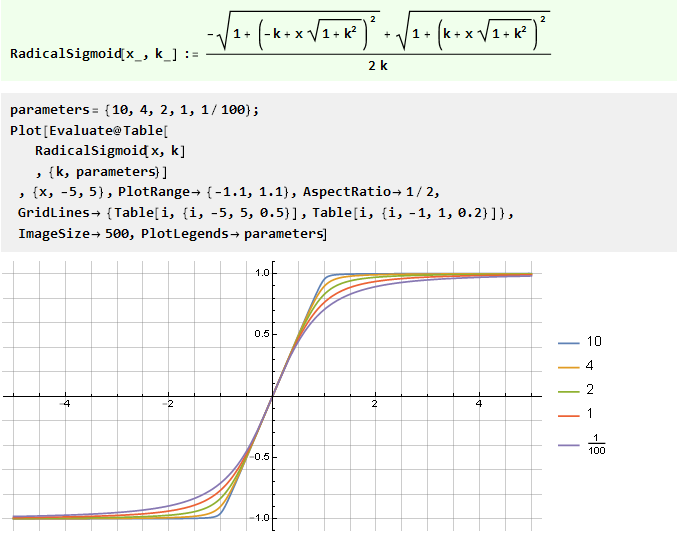
De la función de error generalizado:
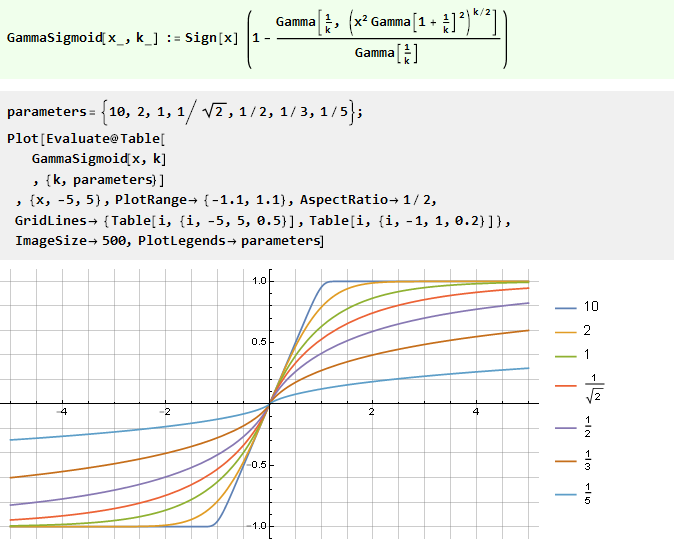
Integración de un polinomio racional:
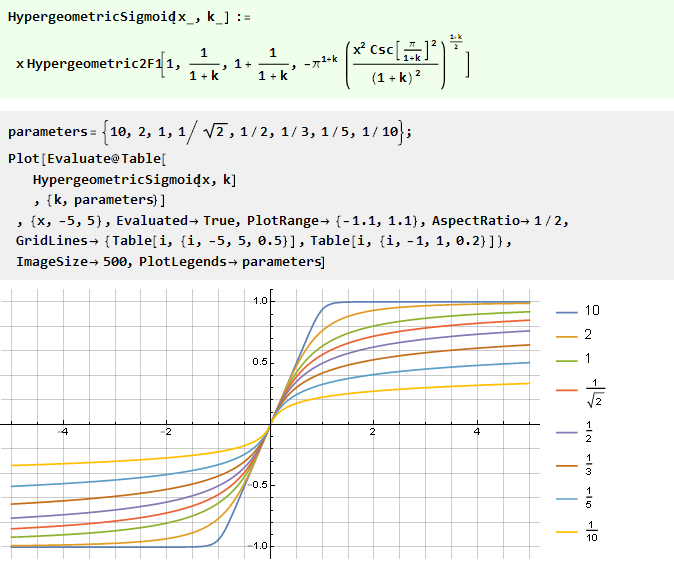
Curiosamente, su caso especial es arcotangente:

Conclusión
La construcción de tales funciones puede ser una tarea fascinante, durante la cual se obtendrán fórmulas simples y complejas, hermosas y no muy hermosas. Puede parecer que todos son muy similares entre sí y no hay necesidad de tal variedad. Este no es necesariamente el caso.
La diferencia puede ser más visible en otras escalas, por ejemplo, logarítmica. Además, además de las tareas indicadas en el encabezado, se pueden usar funciones similares también en otras tareas: mezclar señales, cuando la atenuación suave de una señal se combina con el aumento suave de otra, o la construcción de filtros acústicos, y luego la diferencia se percibirá por el oído o para construir gradientes. - y luego la diferencia se percibirá a simple vista. Además, también se pueden utilizar como donantes para otras funciones más complejas, por ejemplo,
ventana .
En conclusión, vale la pena aclarar algunos puntos más.
Todas las funciones aquí se definieron en el rango de -1 a 1. Si necesita un rango diferente (por ejemplo, de 0 a 1), puede contarse fácilmente ya sea manualmente:
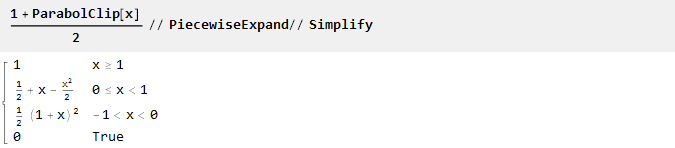
O usando la función de zoom incorporada:

Y para facilitar la exportación de las fórmulas obtenidas al código del programa, la función CForm puede ser útil:
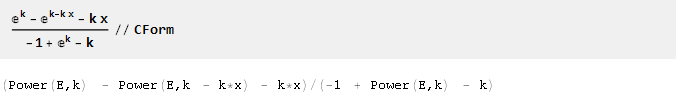
El documento fuente de Mathematica se puede descargar
aquí .
Notas:
[1] Un verdadero matemático sin duda podrá probar rigurosamente (o refutar) esta afirmación.
[2] las funciones hipergeométricas no se consideran en el curso estándar del análisis matemático.
[3] esta sobrecarga se define solo para una unidad de caracteres; no se reconocerá una unidad en formato de coma flotante (por ejemplo, al trazar un gráfico).