Curso MIT "Seguridad de sistemas informáticos". Lección 10: Ejecución simbólica, parte 3

Instituto de Tecnología de Massachusetts. Conferencia Curso # 6.858. "Seguridad de los sistemas informáticos". Nikolai Zeldovich, James Mickens. Año 2014

Computer Systems Security es un curso sobre el desarrollo e implementación de sistemas informáticos seguros. Las conferencias cubren modelos de amenazas, ataques que comprometen la seguridad y técnicas de seguridad basadas en trabajos científicos recientes. Los temas incluyen seguridad del sistema operativo (SO), características, gestión del flujo de información, seguridad del idioma, protocolos de red, seguridad de hardware y seguridad de aplicaciones web.

Lección 1: "Introducción: modelos de amenaza" Parte 1 / Parte 2 / Parte 3
Lección 2: "Control de ataques de hackers" Parte 1 / Parte 2 / Parte 3
Lección 3: “Desbordamientos del búfer: exploits y protección” Parte 1 / Parte 2 / Parte 3
Lección 4: “Separación de privilegios” Parte 1 / Parte 2 / Parte 3
Lección 5: “¿De dónde vienen los sistemas de seguridad?” Parte 1 / Parte 2
Lección 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Lección 7: “Sandbox de cliente nativo” Parte 1 / Parte 2 / Parte 3
Lección 8: "Modelo de seguridad de red" Parte 1 / Parte 2 / Parte 3
Lección 9: "Seguridad de aplicaciones web" Parte 1 / Parte 2 / Parte 3
Lección 10: “Ejecución simbólica” Parte 1 / Parte 2 / Parte 3

Ahora, siguiendo la rama hacia abajo, vemos la expresión t = y. Como estamos considerando una ruta a la vez, no tenemos que introducir una nueva variable para t. Simplemente podemos decir que dado que t = y, entonces t ya no es 0.

Continuamos moviéndonos hacia abajo y llegamos al punto donde llegamos a otra rama. ¿Cuál es la nueva suposición que debemos hacer para seguir por este camino? Esta es una suposición de que t <y.

¿Qué es t? Si busca la rama derecha, veremos que t = y. Y en nuestra tabla, T = y e Y = y. Se deduce lógicamente de esto que nuestra restricción se ve como y <y, que no puede ser.



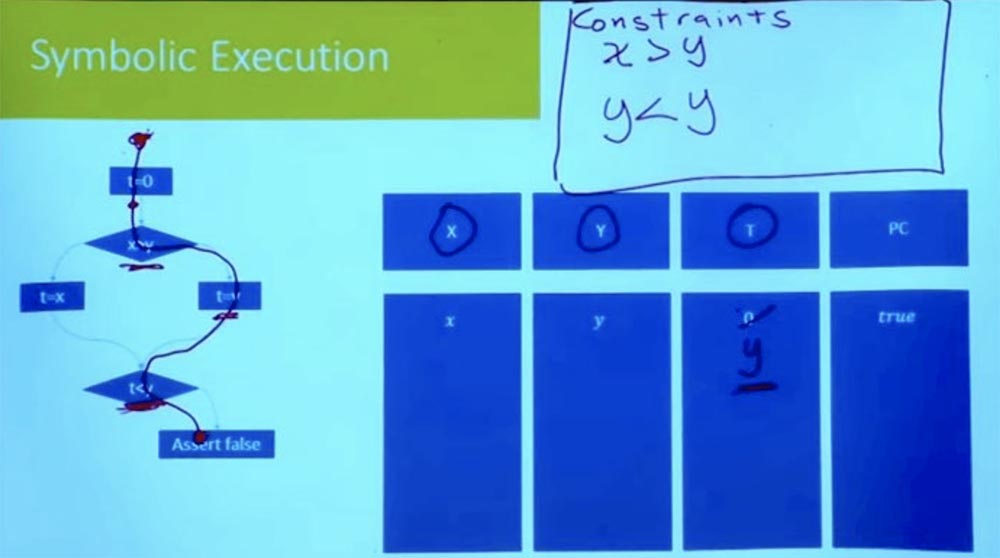
Por lo tanto, teníamos todo en orden hasta llegar a este punto t <y. Hasta que lleguemos a la afirmación falsa, tenemos todas las desigualdades para ser correctas. Pero esto no funciona, porque al realizar tareas de la rama correcta, tenemos una inconsistencia lógica.

Tenemos lo que a menudo se llama la condición del camino. Esta condición debe ser cierta para que el programa siga este camino. Pero sabemos que esta condición no se puede cumplir, por lo tanto, es imposible que el programa siga este camino. Por lo tanto, este camino ahora se ha eliminado por completo, y sabemos que este camino correcto no se puede recorrer.

¿Qué hay de la otra manera? Intentemos pasar por la rama izquierda de una manera diferente. ¿Cuáles serán las condiciones para este camino? Nuevamente, nuestro estado simbólico comienza en t = 0, y X e Y son iguales a las variables x e y.



¿Cómo se ve la restricción de ruta en este caso ahora? Denotamos la rama izquierda como Verdadero, y la rama derecha como Falso y además consideramos el valor t = x. Como resultado del procesamiento lógico de las condiciones t = x, x> y y t <y, obtenemos que simultáneamente tenemos lo que x> y y x <y.



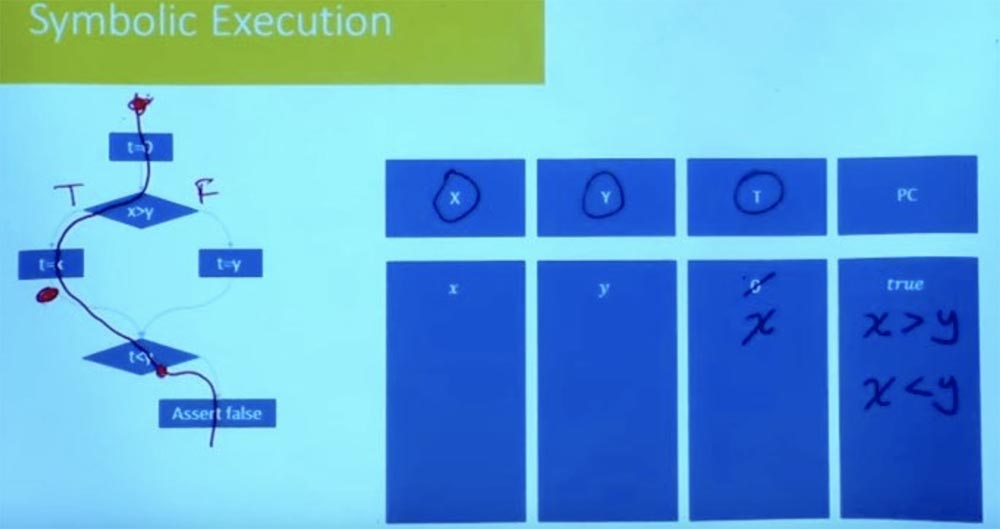
Está claro que esta condición del camino no es satisfactoria. No podemos tener x que sea más grande y más pequeño que y. No hay asignación a una variable X que satisfaga ambas restricciones. Por lo tanto, esto nos dice que la otra forma también es insatisfactoria.

Resulta que en este momento exploramos todos los caminos posibles en el programa que podrían llevarnos a este estado. De hecho, podemos establecer y verificar que no hay una forma posible que nos lleve a la declaración falsa.
Público: en este ejemplo, demostró que estudió el progreso de un programa en todas las ramas posibles. Pero una de las ventajas de la ejecución simbólica es que no necesitamos estudiar todas las rutas exponenciales posibles. Entonces, ¿cómo evitar esto en este ejemplo?

Profesor: Esta es una muy buena pregunta. En este caso, se compromete entre la ejecución del personaje y cuán específico quiere ser. Entonces, en este caso, no estamos usando tanto la ejecución simbólica como la primera vez que miramos el flujo del programa en ambas ramas simultáneamente. Pero gracias a esto, nuestras limitaciones se han vuelto muy, muy simples.

Las restricciones individuales "de una manera tras otra" son muy simples, pero hay que hacerlo una y otra vez, estudiando todas las ramas existentes, y exponencialmente, y todas las formas posibles.
Hay exponencialmente muchas rutas, pero para cada ruta en su conjunto, también hay un conjunto exponencialmente grande de datos de entrada que pueden ir por esa ruta. Entonces, esto ya le da una gran ventaja, porque en lugar de intentar todas las entradas posibles, está intentando hacerlo de todas las formas posibles. ¿Pero puedes hacer algo mejor?

Esta es una de las áreas donde se ha realizado mucha experimentación con respecto a la ejecución simbólica, por ejemplo, la ejecución simultánea de varios caminos. En los materiales de la conferencia conociste la heurística y un conjunto de estrategias que los experimentadores usaron para hacer que la búsqueda sea más solucionable.

Por ejemplo, una de las cosas que hacen es que exploran de una manera tras otra, pero no lo hacen completamente a ciegas. Verifican las condiciones de la ruta después de cada paso dado. Supongamos que aquí en nuestro programa, en lugar de decir "falso", habría un árbol complejo de programas, un gráfico de flujo de control.



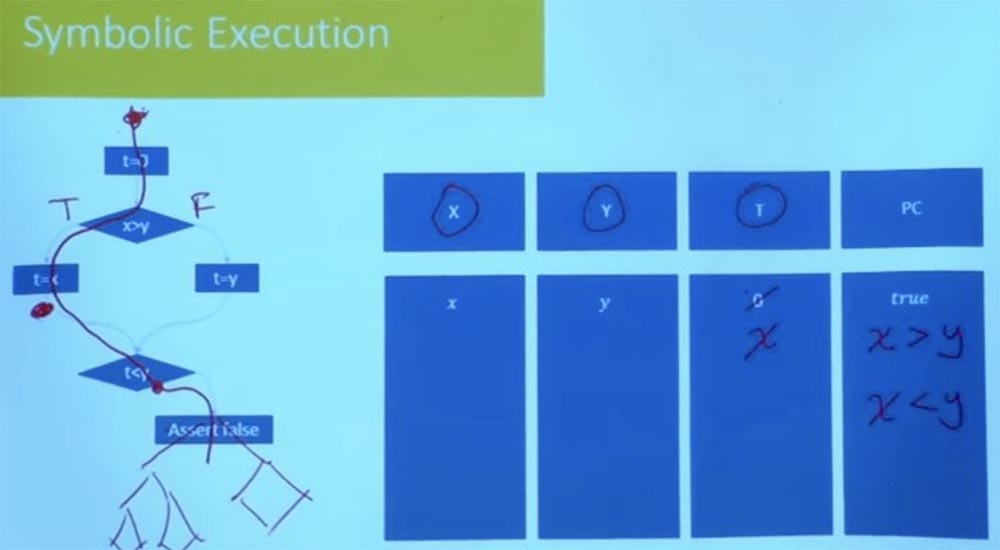
No necesita esperar hasta llegar al final para verificar que este camino sea factible. En ese momento, cuando alcanza la condición t <y, ya sabe que este camino no es satisfactorio, y nunca irá en esa dirección. Por lo tanto, cortar las ramas incorrectas al comienzo del programa reduce la cantidad de trabajo empírico. La exploración razonable de la ruta evita la posibilidad de fallas en el programa en el futuro. Muchas de las herramientas prácticas que se usan hoy en día comienzan principalmente con pruebas aleatorias para obtener el conjunto inicial de caminos, después de lo cual comenzarán a explorar los caminos en el vecindario. Procesan muchas opciones para la posible ejecución del programa para cada una de las ramas, preguntándose qué sucede en estos caminos.

Es especialmente útil si tenemos un buen conjunto de pruebas. Ejecutas tu prueba y descubres que este código no se está ejecutando. Por lo tanto, puede tomar la ruta más cercana a la implementación del código y preguntar si esta ruta se puede cambiar para que vaya en la dirección correcta.



Pero en el momento en que intentas hacer todos los caminos al mismo tiempo, comienzan las restricciones que se vuelven intratables. Por lo tanto, lo que puede hacer es realizar una función a la vez, mientras que puede aprender todos los caminos en una función juntos. Si intenta hacer bloques grandes, en general puede explorar todas las formas posibles.

Lo más importante es que para cada rama verifique sus restricciones y determine si esta rama realmente puede ir en ambos sentidos. Si ella no puede seguir ambos caminos, ahorrará tiempo y esfuerzo al no seguir en la dirección donde no puede ir. Además, no recuerdo las estrategias específicas que utilizan para encontrar formas que tienen más probabilidades de producir muy buenos resultados. Pero cortar las ramas incorrectas en la etapa inicial es muy importante.

Hasta ahora, hemos estado hablando principalmente sobre "código de juguete", sobre variables enteras, sobre ramas, sobre cosas muy simples. Pero, ¿qué sucede cuando tienes un programa más complejo? En particular, ¿qué sucede cuando tienes un programa que incluye un montón?



Históricamente, el montón de moda ha sido la maldición de todos los análisis de software, porque las cosas limpias y elegantes de la época de Fortran explotan por completo cuando intentas ejecutarlas usando programas C en los que asignas memoria de izquierda a derecha. Allí tiene superposiciones y todo el desorden asociado con el programa con memoria asignada y punteros aritméticos. Esta es una de las áreas donde la ejecución simbólica tiene una capacidad sobresaliente para razonar sobre los programas.

Entonces, ¿cómo hacemos esto? Olvidemos las ramas y el flujo de control por un momento. Tenemos un programa simple aquí. Asigna algo de memoria, la anula y obtiene un nuevo puntero y del puntero x. Luego escribe algo a y y comprueba si el valor almacenado en el puntero y es igual al valor almacenado en el puntero x?

Con base en un conocimiento básico de C, puede ver que esta verificación no se realiza porque x se restablece yy = 25, por lo que x indica una ubicación diferente. Hasta ahora, todo está bien con nosotros.
La forma en que modelamos el montón, y la forma en que se modela el montón en la mayoría de los sistemas, utiliza la representación del montón en C, donde es solo una base de direcciones gigantesca, una matriz gigantesca en la que puede colocar sus datos.
Esto significa que podemos representar nuestro programa como un conjunto de datos global muy grande, que se llamará MEM. Esta es una matriz que esencialmente va a asignar direcciones a valores. Una dirección es solo un valor de 64 bits. ¿Y qué pasará después de leer algo de esta dirección? Depende de cómo modeles la memoria.

Si lo modelas a nivel de byte, obtienes un byte. Si lo modelas a nivel de palabra, obtienes una palabra. Dependiendo del tipo de errores que le interesen, y dependiendo de si le preocupa la asignación de memoria o no, la modelará de manera un poco diferente, pero generalmente la memoria es solo una matriz de dirección a valor.



Entonces la dirección es solo un número entero. En cierto modo, no importa lo que C piense de la dirección, es solo un número entero de 64 o 32 bits, dependiendo de su máquina. Es simplemente un valor que está indexado en esta memoria. Y lo que puedes poner en la memoria, puedes leerlo desde esa memoria.

Por lo tanto, cosas como la aritmética de puntero se convierten en aritmética de enteros. En la práctica, hay algunas dificultades, porque en C, la aritmética del puntero sabe acerca de los tipos de puntero, y aumentarán en proporción al tamaño. Entonces, como resultado, obtenemos la siguiente línea:

y = x + 10;  sizeof (int)



Pero lo que realmente importa es lo que sucede cuando escribes y lees de memoria. Basado en el puntero de que 25 debería escribirse en y, tomo una matriz de memoria y la indexo con y. Y escribo 25 en esta ubicación de memoria.

Luego paso a la declaración MEM [y] = MEM [x], leo el valor de la ubicación y en la memoria, leo el valor de la ubicación x en la memoria y los comparo entre sí. Así que verifico si coinciden o no.

Esta es una suposición muy simple, que le permite cambiar de un programa que usa heap a un programa que usa esta gigantesca matriz global que representa la memoria. Esto significa que ahora, cuando se habla de programas que administran el montón, realmente no es necesario hablar de programas que administran el montón. Lograrás hablar perfectamente sobre matrices y no sobre montones.

Aquí hay otra pregunta simple. ¿Qué pasa con la función malloc? Simplemente puede tomar y usar la implementación de malloc en C, realizar un seguimiento de todas las páginas resaltadas, realizar un seguimiento de todo lo que se ha liberado, simplemente tener una lista gratuita y eso es suficiente. Resulta que para muchos propósitos y para muchos tipos de errores no necesita malloc para ser complejo.

De hecho, puede cambiar de malloc, que se ve así: x = malloc (sizeof (int) * 100), a malloc de este tipo:

POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}

Lo que simplemente dice: "Voy a guardar el contador para el próximo espacio libre en la memoria, y cada vez que alguien solicita una dirección, le doy esta ubicación y la aumento, y luego devuelvo rv". En este caso, lo que malloc en el sentido tradicional se ignora por completo.



En este caso, no hay liberación de memoria. La función simplemente continúa moviéndose más y más lejos de la memoria, y más y más, y aquí es donde termina sin ninguna liberación. Tampoco le importa que haya áreas de memoria en las que no valga la pena escribir, porque hay direcciones especiales de especial importancia reservadas para el sistema operativo.

No modela nada que haga que la escritura de la función malloc sea complicada, pero solo a un cierto nivel de abstracción, cuando intentas hablar sobre algún tipo de código complejo que realiza manipulaciones de puntero.

Al mismo tiempo, no le importa liberar memoria, pero le preocupa si el programa va a escribir, por ejemplo, fuera de un búfer, en cuyo caso esta función malloc puede ser bastante buena.



Y esto realmente sucede muy, muy a menudo cuando haces una ejecución simbólica de código real. Un paso muy importante es modelar las funciones de su biblioteca. La forma en que modela las funciones de la biblioteca tendrá un gran impacto, por un lado, en el rendimiento y la escalabilidad del análisis, pero por otro lado, también afectará la precisión.

Entonces, si tiene un modelo de "juguete" malloc, como este, actuará muy rápidamente, pero al mismo tiempo habrá ciertos tipos de errores que no podrá notar. Entonces, por ejemplo, en este modelo ignoro completamente las distribuciones, por lo que puedo obtener un error si alguien tiene acceso al espacio no asignado. Por lo tanto, en la vida real, nunca usaré este modelo malloc de Mickey Mouse.

Por lo tanto, siempre hay un equilibrio entre la precisión del análisis y la eficiencia. Y cuanto más complejos son los modelos de funciones estándar, como malloc, menos escalable es su análisis. Pero para algunas clases de error necesitará estos modelos simples. Por lo tanto, varias bibliotecas en C son de gran importancia, que son necesarias para comprender lo que realmente hace un programa de este tipo.

Por lo tanto, redujimos el problema de razonar sobre el montón al razonar sobre el programa con matrices, pero realmente no le dije cómo razonar sobre el programa con matrices. Resulta que la mayoría de los solucionadores SMT admiten la teoría de matrices.



La idea es que si a es una matriz, entonces hay alguna notación que le permite tomar esta matriz y crear una nueva matriz, donde la ubicación i se actualiza al valor e. ¿Eso está claro?

Por lo tanto, si tengo una matriz a, y hago esta operación de actualización, y luego trato de leer el valor de k, entonces esto significa que el valor de k será igual al valor de k en la matriz a, si k es diferente de i, y será igual a e, si k es igual a i.

Actualizar una matriz significa que necesita tomar la matriz anterior y actualizarla con una nueva matriz. Bueno, si tiene una fórmula que incluye la teoría de las matrices, es por eso que comencé con una matriz cero, que en todas partes está representada simplemente por ceros.



Luego escribo 5 en la ubicación iy 7 en la ubicación j, después de lo cual leo de k y verifico si es 5 o no. Luego se puede expandir usando la definición de algo que dice, por ejemplo: “si k es iyk es y, mientras que k es diferente de j, entonces sí será 5, de lo contrario no será 5 ".

Y en la práctica, los solucionadores SMT no solo expanden esto a muchas fórmulas booleanas, sino que usan esta estrategia de ida y vuelta entre el solucionador SAT y el motor, que puede hablar sobre la teoría de matrices para llevar a cabo este trabajo.

Lo importante es que confiando en esta teoría de matrices, utilizando la misma estrategia que aplicamos para generar fórmulas para enteros, en realidad puede generar fórmulas que incluyen lógica de matriz, actualizaciones de matriz, ejes de matriz, iteración de matriz. Y siempre que corrija su camino, estas fórmulas son muy fáciles de generar.
Si no corrige sus rutas, pero desea crear una fórmula que corresponda al paso del programa por todas las rutas, entonces esto también es relativamente fácil. Lo único con lo que tiene que lidiar es con un tipo especial de bucles.

Los diccionarios y mapas también son muy fáciles de modelar utilizando funciones indefinidas. En realidad, la teoría de las matrices en sí es solo un caso especial de una función indefinida. Con la ayuda de tales funciones, se pueden hacer cosas más complicadas. En el solucionador SMT moderno, hay soporte incorporado para razonar sobre conjuntos y operaciones de conjuntos, lo que puede ser muy útil si se trata de un programa que incluye el cálculo de conjuntos.

Al diseñar una de estas herramientas, la fase de modelado es muy importante. Y el punto no es solo cómo modela las funciones complejas del programa hasta sus teorías, por ejemplo, cosas como reducir los montones a matrices. El punto también es qué teorías y solucionadores usas. Hay una gran cantidad de teorías y solucionadores con diferentes relaciones, para lo cual es necesario elegir un compromiso razonable entre eficiencia y costo.



La mayoría de las herramientas prácticas se adhieren a la teoría de los vectores de bits y, si es necesario, pueden usar la teoría de las matrices para modelar montones. En general, las herramientas prácticas intentan evitar teorías más complejas, como la teoría de conjuntos. Esto se debe a que generalmente son menos escalables en algunos casos, si no se trata de un programa que realmente requiere este tipo de herramienta para funcionar.

Audiencia: además del estudio del rendimiento simbólico, ¿en qué se centran los desarrolladores?

: — , . , , , , . , .

, , . , , , , , , , .

, — , , . , , — , JavaScript Python, . , .



, Python. , , : «, , , ». .

, , , , , .
, , , - , , .

, , , . , , Microsoft Word, , , .

, , , , .

, . , , - , - . , , . , .


La versión completa del curso está disponible aquí .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps hasta diciembre de forma gratuita al pagar por un período de seis meses, puede ordenar aquí .

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?