Curso MIT "Seguridad de sistemas informáticos". Lección 10: Ejecución simbólica, parte 2

Instituto de Tecnología de Massachusetts. Conferencia Curso # 6.858. "Seguridad de los sistemas informáticos". Nikolai Zeldovich, James Mickens. Año 2014

Computer Systems Security es un curso sobre el desarrollo e implementación de sistemas informáticos seguros. Las conferencias cubren modelos de amenazas, ataques que comprometen la seguridad y técnicas de seguridad basadas en trabajos científicos recientes. Los temas incluyen seguridad del sistema operativo (SO), características, gestión del flujo de información, seguridad del idioma, protocolos de red, seguridad de hardware y seguridad de aplicaciones web.

Lección 1: "Introducción: modelos de amenaza" Parte 1 / Parte 2 / Parte 3
Lección 2: "Control de ataques de hackers" Parte 1 / Parte 2 / Parte 3
Lección 3: “Desbordamientos del búfer: exploits y protección” Parte 1 / Parte 2 / Parte 3
Lección 4: “Separación de privilegios” Parte 1 / Parte 2 / Parte 3
Lección 5: “¿De dónde vienen los sistemas de seguridad?” Parte 1 / Parte 2
Lección 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Lección 7: “Sandbox de cliente nativo” Parte 1 / Parte 2 / Parte 3
Lección 8: "Modelo de seguridad de red" Parte 1 / Parte 2 / Parte 3
Lección 9: "Seguridad de aplicaciones web" Parte 1 / Parte 2 / Parte 3
Lección 10: “Ejecución simbólica” Parte 1 / Parte 2 / Parte 3

Audiencia: Parece que no ha hablado sobre cómo se utilizan los bits para almacenar un entero int.

Profesor: Esta es una muy buena pregunta. Y realmente tiene que ver con cómo define sus limitaciones, ¿verdad? Por lo tanto, si observa nuestro sencillo ejemplo desde el principio, verá que asumimos la presencia de enteros que estudiamos en la escuela primaria. Al mismo tiempo, decidimos ignorar por completo los errores de desbordamiento. Si le preocupan los errores de desbordamiento y es importante para usted que no existan tales errores, el uso de números enteros matemáticamente no ayudará a solucionar el problema.



Lo que necesita es presentar estas cantidades no como enteros, sino como vectores de bits. Cuando los representa como vectores de bits, debe usar una vista más amplia de las cosas. Aquí volvemos a los solucionadores SMT. Un aspecto de la teoría modular es que el solucionador en sí mismo es extensible utilizando diferentes teorías.

Las teorías más populares son las teorías de vector de bits de longitud fija. Esto significa que si interpreta sus fórmulas en la teoría de los vectores de bits de longitud fija, primero debe establecer la longitud de los vectores de bits. Es decir, debe indicar explícitamente que esto se utilizará para vectores de bits de 32 bits de longitud, u 8 bits, o 64 bits.



Hay otra teoría llamada teoría de la matriz TOA. Y hablaremos un poco más al respecto. A diferencia de la teoría de los vectores de bits, que está diseñada para cosas de una longitud fija, la teoría de las matrices está destinada a colecciones cuyo tamaño es a priori desconocido.

Ahora, en la práctica, nadie usa la teoría de matrices, por ejemplo, para modelar enteros, porque es demasiado costoso. Hablar sobre un problema es mucho más costoso cuando no se conocen sus límites. Por lo tanto, como regla, las personas usan la teoría de una longitud fija de vectores de bits en las discusiones de enteros o incluso símbolos.

Otra teoría muy extendida es la teoría de la aritmética de enteros reales, y en particular la aritmética de enteros lineales.



A la gente le gusta mucho esta teoría porque proporciona una argumentación efectiva, pero no es demasiado buena cuando habla de programas, porque aquí realmente le importan los problemas de desbordamiento. Pero esta teoría es ampliamente utilizada para muchas cosas.

Otra teoría que se usa con frecuencia es la teoría de las funciones no interpretadas. ¿Qué significa esta teoría?



Significa que tienes una cierta fórmula. En esta fórmula, sabe que está llamando a una función, pero no sabe nada sobre esta función, excepto por el hecho de que si inserta alguna entrada en ella, obtendrá la misma salida.

Resulta que esto es muy útil cuando se razona sobre cosas como el uso de código de punto flotante, modelado, senos, cosenos, raíces cuadradas. Las discusiones detalladas sobre tales cosas pueden llevar mucho tiempo y ser costosas. Pero usar esta teoría le permite decir: "Mire, no me importa realmente lo que hace la función seno. No me importa qué dirá exactamente. Solo necesito saber que si llamo a la función seno en varios lugares del programa con una entrada específica, obtendré datos del mismo tipo en la salida. Esto es suficiente para que razone sobre mi programa ".

Y, por lo tanto, las operaciones más comunes en el análisis de sistemas reales son los vectores de bits que funcionan con enteros, registros y punteros. De hecho, los punteros a menudo están representados por un número entero, porque a veces no establece vectores de bits en los punteros. Pero a veces tienes que hacer esto, y luego ya no puedes usar números enteros.

Entonces, examinamos lo que un solucionador SMT puede hacer por usted. ¿Cómo funciona realmente? ¿Qué hay dentro de ellos que los hace funcionar?

De hecho, los solucionadores de SMT confían en nuestra capacidad para resolver los problemas de viabilidad de las fórmulas booleanas SAT, en la capacidad de considerar problemas asociados solo con restricciones puramente booleanas y variables booleanas, y decirnos si se asegurará de que el programa asigne los valores asignados a estas variables booleanas o no .

Esto es algo que durante muchos, muchos años enseñó a estudiantes de último año, diciendo que en realidad es una tarea completa de NP, y en los casos en que algo se reduce a SAT, no debe hacer esto. Pero resulta que en realidad tenemos muy buenos solucionadores de SAT.

Entonces, te diré la idea básica de cómo funcionan los solucionadores SAT. Se basa en el hecho de que toma todas sus restricciones sobre las variables booleanas y las coloca en la base de datos. Es posible que no pueda ver las letras pequeñas en la pantalla con claridad, pero eso es todo lo que puedo hacer.



Comentaré y hablaré al respecto en el curso de la acción, y luego publicaré las diapositivas para que pueda ver lo que está escrito allí.

Entonces, aquí en la tarea SAT tenemos todas estas variables que representan incógnitas booleanas, ¿verdad? Queremos saber si es posible que X sea verdadero al mismo tiempo (X = VERDADERO) e Y sea verdadero y Z sea verdadero. Estas son nuestras incógnitas. Además, todas las restricciones están en forma conjuntiva normal. Esto significa que todas nuestras restricciones tienen la forma de X1 = verdadero o X2 = verdadero o X3 = verdadero.



De esta forma, tenemos todas nuestras limitaciones, que dicen que X1 es verdadero o X2 es falso o X3 es falso. Probablemente recuerde de matemáticas discretas que cualquier fórmula booleana se puede representar en forma conectiva normal. Esto significa que cualquier representación que use para representar fórmulas booleanas, puede convertirla fácilmente a este formato.

Entonces, tenemos una base de datos con muchas limitaciones de este formulario. El solucionador SAT elegirá una de estas variables al azar, supongamos que es X1. Y él dirá: “¿por qué no establecer X1 en verdadero? No sé nada sobre estas restricciones, así que puedo suponer que esto es así ". Y luego sucede que tendrá restricciones que, por ejemplo, indican que X1 es falso o X7 es verdadero.

Entonces, si sabes que X1 es verdadero y sabes que X1 es falso o X7 es verdadero, ¿qué sabes sobre X7?

Público: debe ser cierto!

Profesor: sí, debe ser cierto. Porque de lo contrario esta restricción no se cumplirá. Entonces, ahora ha distribuido este valor de X1 a X7. Supongamos que ahora selecciona otra variable aleatoria, como X5.



Ahora suponga que tiene una restricción que dice: X7 es falso o X6 es verdadero o X5 es falso. Entonces, tengo X5 = verdadero y X7 = verdadero. Esto significa que X6 ahora también debería ser cierto. Porque de lo contrario se violaría esta restricción. Entonces, el sistema concluye que X6 debería ser verdadero y continúa el proceso, realizando las comprobaciones disponibles y mirando todas las ofertas disponibles. El sistema verifica si hay otras cosas que están implícitas en las verificaciones que tiene. Y ella sigue estos significados hasta que sucede una de dos cosas.

La primera es que continúas siguiendo las consecuencias e intentas cosas al azar, y finalmente estableces el valor para cada variable sin encontrar una contradicción. Entonces hiciste todo bien.

El segundo: te enfrentas a una contradicción y luego regresas a la condición que hizo que X4 sea verdadero, excluyendo la condición que causó que X4 sea falso. Pero hay una regla de álgebra booleana que todos deberían saber: una variable no puede ser verdadera y falsa al mismo tiempo.



Y dice que te enfrentas a una contradicción, obviamente hiciste algo mal en una de estas tareas aleatorias que intentaste completar.

Analicemos esta contradicción y veamos qué tipo de tareas llevaron a esta contradicción. Sobre la base de las tareas que llevaron a esta contradicción, vamos a llegar a una nueva cláusula de conflicto que resume esta contradicción.

¿Qué sucede que X1 es falso, y X5 es falso y X9 también es falso? Esencialmente, esto se basa en lo que aprendí de estas asignaciones aleatorias, durante las cuales descubrí que una de estas cosas debe ser verdadera, que no puede ser que X1 sea verdadero y X5 sea verdadero, y X9 fue falso, esto no puede ser.

Sé que esto no puede suceder, porque cuando intenté hacerlo, todo "explotó", terminé el programa con una contradicción.

Y así, el solucionador de SAT intenta completar tareas aleatorias, verificando cómo van. Cuando encuentra contradicciones, analiza el conjunto de consecuencias que condujeron a estas contradicciones, y finalmente forma una nueva restricción que asegura que el solucionador nunca más encuentre esta contradicción particular, este problema particular.
Por lo tanto, podemos imaginar el solucionador SAT como un "cuadro negro" que proporciona una restricción booleana y puede decir si es satisfactoria o no. Los solucionadores SMT están construidos sobre los mejores solucionadores SAT. Pueden usar el poder de los solucionadores de SAT para resolver problemas de NP completo con razonamiento orientado a temas sobre teorías compatibles.

Para tener una idea de cómo funciona esto, suponga que tiene esa fórmula.



¿Es factible? ¿Podemos encontrar una prueba satisfactoria para ella? El solucionador SMT puede separar parte de esta fórmula, lo que requiere razonamiento en la teoría de enteros. Utilizamos estructuras booleanas para separar fórmulas. Entonces tenemos las fórmulas F1, F2, F3 y F4.



Ahora bien, esta es una tarea booleana puramente lógica. ¿Puedo encontrar una tarea satisfactoria para esto? El solucionador de SAT puede decir: "sí, puedo encontrar algo que satisfaga esta tarea haciendo F1 = verdadero, F2 = verdadero y F3 = verdadero". Esto satisface la especificación de la fórmula booleana.

\

Entonces, ahora tenemos una pregunta que podemos hacerle al solucionador para un área específica, en este caso es solo un solucionador aritmético lineal. Entonces podemos ir al solucionador lineal de Solucionador de teoría y decir: "El solucionador de SAT afirma que esta es una tarea razonable, y que si puedo hacer que esta tarea funcione, entonces mi fórmula estará satisfecha".

Puedo decir que F1 es X> 5, F2 es Y <5 y F3 es Y> X. Así que puedo preguntarle al solucionador SAT si es posible obtener ese X e Y para que X sea> 5, Y sea < 5, y en este caso Y sería> X? Ahora bien, esta es una cuestión de aritmética puramente lineal, no hay lógica booleana.

¿Y cuál es la respuesta a esta pregunta? No Es imposible satisfacer estas condiciones al mismo tiempo.
Entonces, hay métodos tradicionales para resolver problemas lineales. Puede usar el método simplex, por ejemplo, para resolver sistemas de desigualdades lineales. Existen muchos métodos que pueden usarse para resolver sistemas de desigualdades lineales.



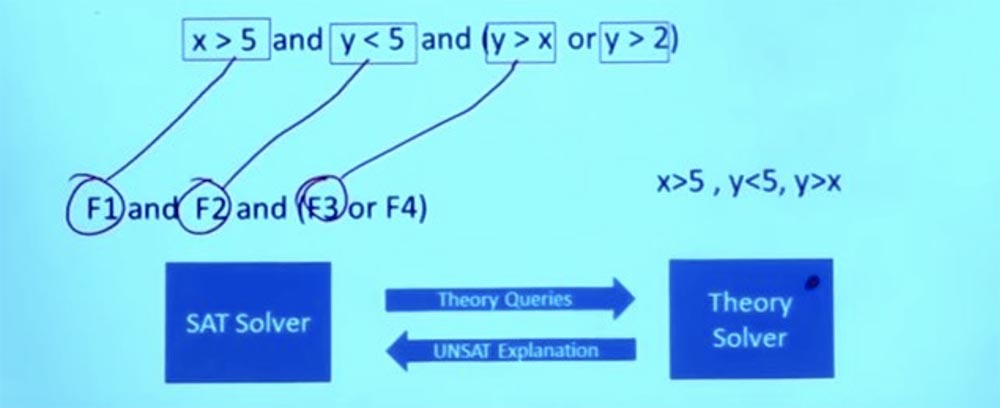
Entonces, el solucionador SAT envía preguntas teóricas al solucionador de teoría. La conclusión es que los solucionadores de teorías saben todo sobre estos problemas y pueden dar una respuesta precisa a la pregunta de si estas condiciones funcionarán.

En este caso, el solucionador teórico procesa la solicitud, descubre que esta asignación de condición no puede funcionar, vuelve al solucionador SAT y dice: "¡esas cosas que hiciste no funcionarán"!

Pero él no solo dice sí o no, sino que explica por qué algo no funcionará. Por el hecho de que estas fórmulas no funcionan, el solucionador de teoría concluye que F1 y F2 y F3 no pueden existir simultáneamente, y le dice al solucionador SAT que estas 3 fórmulas son mutuamente excluyentes.

Así que ahora tenemos parte de la información que puedo devolver al solucionador de SAT y preguntarle: "oye, puedes darme una solución que satisfaga no solo la restricción que teníamos al principio, sino también la nueva restricción que descubrió Theory solucionador "?

¿Hay algún otro propósito que ahora satisfaga ambas limitaciones?



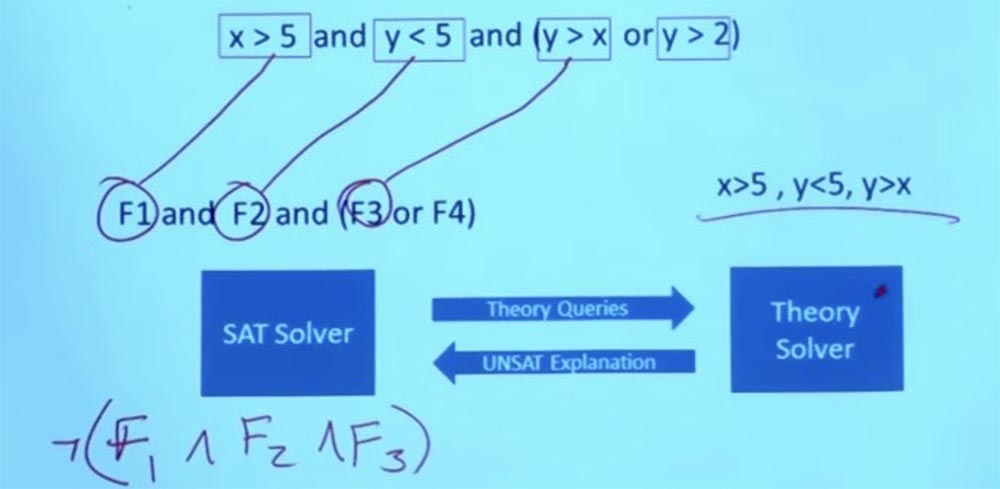
Entonces, descartamos la restricción inicial X> 5, Y <5, Y> X, esto ya no nos molesta.



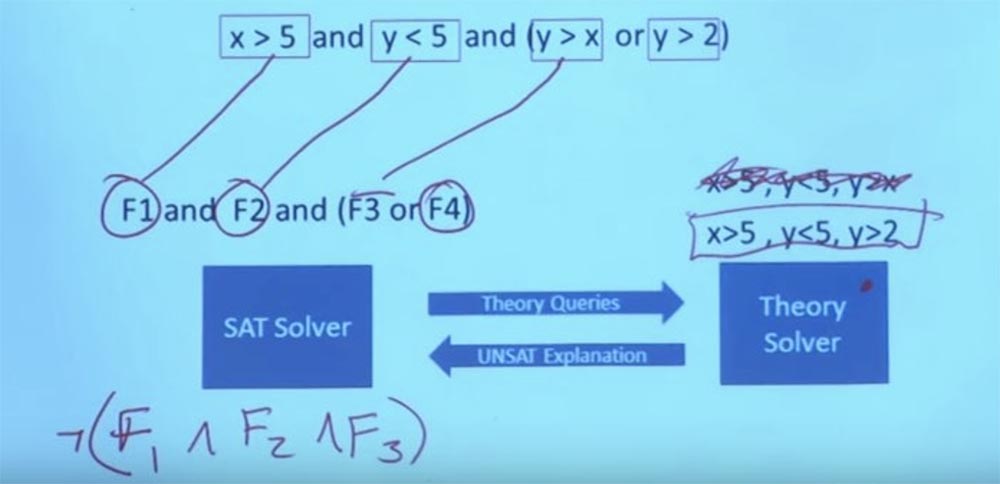
Tenemos una nueva restricción que podemos establecer en nuestro solucionador de teoría: X> 5, Y <5, Y> 2. Podemos hacer que Y sea igual a 3 y X igual a 6, y luego funcionará. Ahora tiene una tarea que satisface la fórmula en teoría y satisface la estructura booleana de este propósito. Y con eso, el sistema puede volver y decir: "sí, esta es la tarea que satisface todas sus limitaciones". Esta es la interacción entre el solucionador de teorías y el solucionador de SAT. En realidad, esto significa poder hablar sobre fórmulas booleanas muy, muy grandes y muy complejas. Esto es lo que hace posible la ejecución simbólica.

Ahora consideraremos la siguiente pregunta: ¿cómo se lleva a cabo la transición del programa a las restricciones que podemos proporcionar al solucionador SMT?

Público: ¿Se está completando o no la construcción de un solucionador SMT NP?

Profesor: El solucionador SMT es esencialmente un problema canónico de NP completo. Pero la mayoría de los solucionadores en estos días incluyen soporte para ciertas teorías que son completamente irresolubles.

Audiencia: ¿cómo aborda este problema en su sistema?

Profesor: bueno, al final, obtendrá una restricción creada a partir de este programa. Se lo darás al solucionador SMT. Y el hecho de que se trata de tareas NP-complete o el hecho de que no son satisfactorias significa que si tiene suerte, recibirá una respuesta en cuestión de segundos. Pero si tienes mala suerte, entonces puede llevar más tiempo que la creación del universo.



Audiencia: ¿sucede que las tareas del sistema lineal no pasan el SAT?

Profesor: sí, eso realmente sucede. Sin embargo, las herramientas de ingeniería existentes lo hacen menos común. No resolvemos problemas aleatorios de SAT, no resolvemos problemas completamente aleatorios de vectores de bits.

Resolvemos problemas que tienen una determinada estructura para que una persona pueda verlo y tener la confianza de que funcionará. Estamos tratando de crear algunos argumentos en su cabeza para entender por qué esto funcionó. Y los solucionadores de SAT usan esta estructura. Su problema puede tener un millón de variables booleanas, pero en realidad la mayoría de estas variables dependen mucho de los valores del otro. Por lo tanto, el número de grados de libertad en el problema es en realidad mucho menor de lo que sugieren millones de variables.

Público: usted dice que no se trata de una pregunta de examen, sino de la vida real. Una vez que alguien ha construido este sistema, debería funcionar y tener sentido. Así que probablemente esta no sea una de las críticas teóricas innecesarias.

Profesor: eso es todo. Por lo tanto, en la práctica, cuando usa esta herramienta, lo que siempre hace es establecer tiempos de espera. En general, todo sucede porque la exponencialidad no significa que no se pueda hacer esto. La exponencialidad, es decir, cuando una función está limitada por otra función, simplemente significa que hay una pared de ladrillos frente a la cual estas cosas funcionarán, y funcionarán realmente muy rápidamente. La exponencialidad funciona en ambas direcciones.



Cuando te alejas de este muro, las cosas crecen muy rápido, pero cuando te acercas a problemas más pequeños o más simples, estos problemas también se aceleran muy, muy rápidamente. Esto significa que muchos problemas terminan muy rápidamente. Y luego se produce el tiempo de espera del problema. El punto es diseñar cosas para que entre los problemas que terminan rápidamente estén aquellos que traigan beneficios prácticos. Estos son problemas que lo señalan a las vulnerabilidades de seguridad de su sistema, a errores, a rutas que quizás no haya explorado antes, o a entradas que violarán sus rutas si no las investigó de antemano.

Entonces, sabemos cómo pasar de una fórmula, de un conjunto de restricciones a una respuesta que dice: "sí, esta fórmula tiene una solución, y aquí está, esta es una solución". O él dirá: "esta fórmula no es satisfactoria, porque no hay información que satisfaga sus tareas". Entonces, ¿cómo obtenemos la fórmula del programa?

Cuando haces una ejecución simbólica, vas a la rama y no sabes en qué dirección irá. Hay dos opciones de qué hacer en este caso. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



, , t=0 false.



, , ? : , , .

, , , , , , .

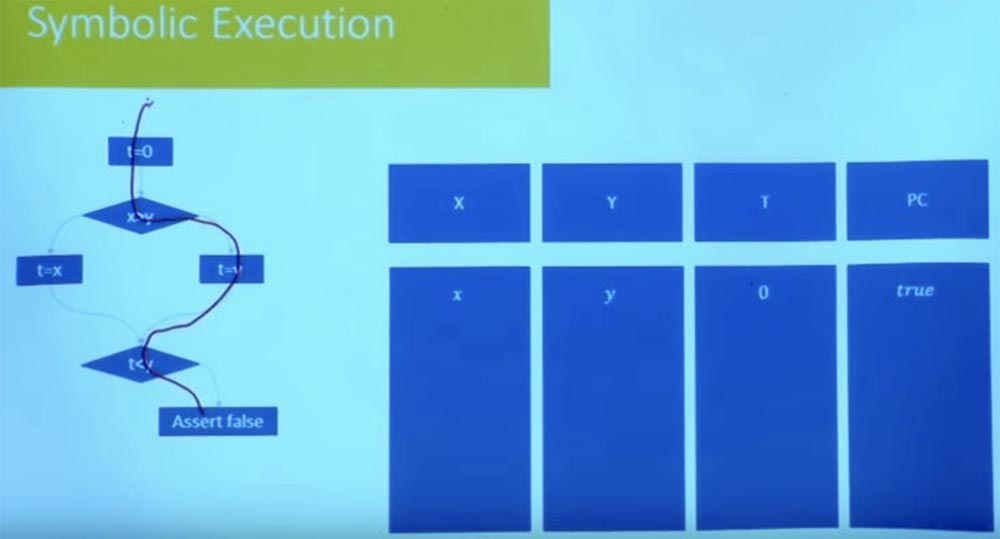
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



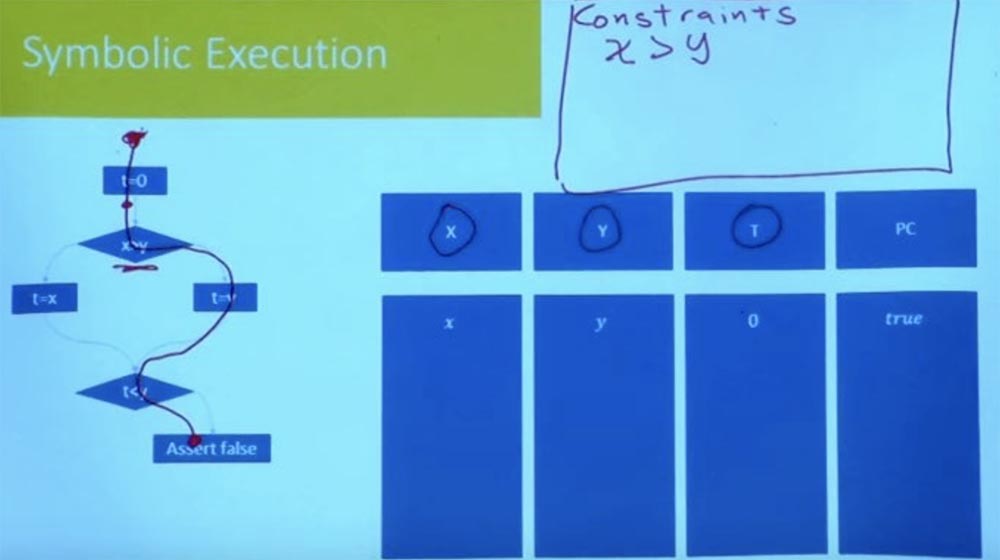
55:00

MIT « ». 10: « », 3


La versión completa del curso está disponible aquí .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps hasta diciembre de forma gratuita al pagar por un período de seis meses, puede ordenar aquí .

Dell R730xd 2 veces más barato? ¡Solo tenemos 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los Estados Unidos! Lea sobre Cómo construir un edificio de infraestructura. clase c con servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?