Identifique el fraude utilizando el conjunto de datos de Enron. Parte 2, encontrar el mejor modelo

Le presento la segunda parte del artículo sobre la búsqueda de presuntos fraudes basados ​​en datos de Enron Dataset. Si no ha leído la primera parte, puede familiarizarse con ella aquí .

Ahora hablaremos sobre el proceso de construcción, optimización y elección de un modelo que dará la respuesta: ¿vale la pena sospechar de una persona de fraude?

Anteriormente, analizamos uno de los conjuntos de datos abiertos que proporciona información sobre sospechosos en el caso de Enron y fraude en él. Además, se corrigió el sesgo en los datos iniciales, se rellenaron los huecos (NaN), después de lo cual se normalizaron los datos y se completó la selección de atributos.

El resultado fue familiar para muchos:

• X_train e y_train: la muestra utilizada para el entrenamiento (111 registros);
• X_test e y_test: una muestra en la que se comprobará la exactitud de las predicciones de nuestros modelos (28 entradas).

Hablando de modelos ... Para predecir correctamente si vale la pena sospechar de una persona, en función de algunos signos que caracterizan sus actividades, utilizaremos la clasificación. Los principales tipos de modelos utilizados para resolver problemas en este segmento se pueden tomar de Sklearn:

• Naive Bayes (clasificador ingenuo de Bayes);
• SVM (máquina de vectores de referencia);
• K-vecinos más cercanos (método para encontrar vecinos más cercanos);
• Bosque aleatorio (bosque aleatorio);
• Red neuronal.

También hay una imagen que ilustra su aplicabilidad bastante bien:

Entre ellos hay un árbol de decisión (árbol de decisión), familiar para muchos, pero, tal vez, no tiene sentido en una tarea usar este método junto con Random Forest, que es un conjunto de árboles de decisión. Por lo tanto, reemplácelo con Regresión logística, que puede actuar como un clasificador y producir una de las opciones esperadas (0 o 1).

Inicio

Inicializamos todos los clasificadores mencionados con valores predeterminados:

from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.neural_network import MLPClassifier from sklearn.ensemble import RandomForestClassifier random_state = 42 gnb = GaussianNB() svc = SVC() knn = KNeighborsClassifier() log = LogisticRegression(random_state=random_state) rfc = RandomForestClassifier(random_state=random_state) mlp = MLPClassifier(random_state=random_state) 

También los agruparemos para que sea más conveniente trabajar con ellos como un agregado, en lugar de escribir código para cada individuo. Por ejemplo, podemos entrenarlos a todos a la vez:

 classifiers = [gnb, svc, knn, log, rfc, mlp] for clf in classifiers: clf.fit(X_train, y_train) 

Después de entrenar a los modelos, llegó el momento de la primera prueba de su calidad de predicción. Además, visualizamos nuestros resultados usando Seaborn:

 from sklearn.metrics import accuracy_score def calculate_accuracy(X, y): result = pd.DataFrame(columns=['classifier', 'accuracy']) for clf in classifiers: predicted = clf.predict(X_test) accuracy = round(100.0 * accuracy_score(y_test, predicted), 2) classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'accuracy': accuracy}, ignore_index=True) print('Accuracy is {accuracy}% for {classifier_name}'.format(accuracy=accuracy, classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='accuracy', palette=cmap, data=result) 

Echemos un vistazo a la idea general de la precisión de los clasificadores:

 calculate_accuracy(X_train, y_train) 

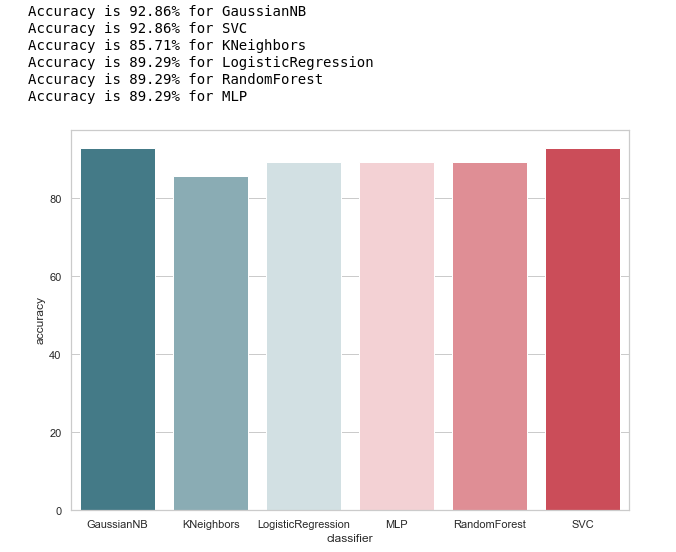
A primera vista, se ve bastante bien, la precisión de las predicciones en la muestra de prueba fluctúa alrededor del 90%. Parece que la tarea es brillante!

 def QuaziAlgo(features): return 0 

Pero aún así, antes de halagarnos, construyamos una matriz de confusión para los resultados de la predicción:

 from sklearn.metrics import confusion_matrix def make_confussion_matrices(X, y): matrices = {} result = pd.DataFrame(columns=['classifier', 'recall']) for clf in classifiers: classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') predicted = clf.predict(X_test) print(f'{predicted}-{classifier}') matrix = confusion_matrix(y_test,predicted,labels=[1,0]) matrices[classifier] = matrix.T return matrices 

Calculamos las matrices de error para cada clasificador y, junto con esto, vemos lo que predijeron:

 matrices = make_confussion_matrices(X_train,y_train) 

Incluso una representación textual del resultado del trabajo de los clasificadores es suficiente para entender que algo claramente salió mal.

El método de vecinos más cercanos no reveló un solo sospechoso en la muestra de prueba. Surgen dos preguntas:

1. ¿Cuál es la razón de este comportamiento del clasificador de KNeighbours?
2. ¿Por qué creamos matrices de error si no las usamos, pero solo miramos los resultados de la predicción?

Echa un vistazo más profundo

Comencemos con la segunda pregunta. Intentemos visualizar nuestras matrices de errores y presentar los datos en formato gráfico para comprender dónde se produce el error de clasificación:

 import itertools from collections import Iterable def draw_confussion_matrices(row,col,matrices,figsize = (16,12)): fig, (axes) = plt.subplots(row,col, sharex='col', sharey='row',figsize=figsize ) if any(isinstance(i, Iterable) for i in axes): axes = list(itertools.chain.from_iterable(axes)) idx = 0 for name,matrix in matrices.items(): df_cm = pd.DataFrame( matrix, index=['True','False'], columns=['True','False'], ) ax = axes[idx] fig.subplots_adjust(wspace=0.1) sns.heatmap(df_cm, annot=True,cmap=cmap,cbar=False ,fmt="d",ax=ax,linewidths=1) ax.set_title(name) idx += 1 

Los mostramos en 2 filas y 3 columnas:

 draw_confussion_matrices(2,3,matrices) 

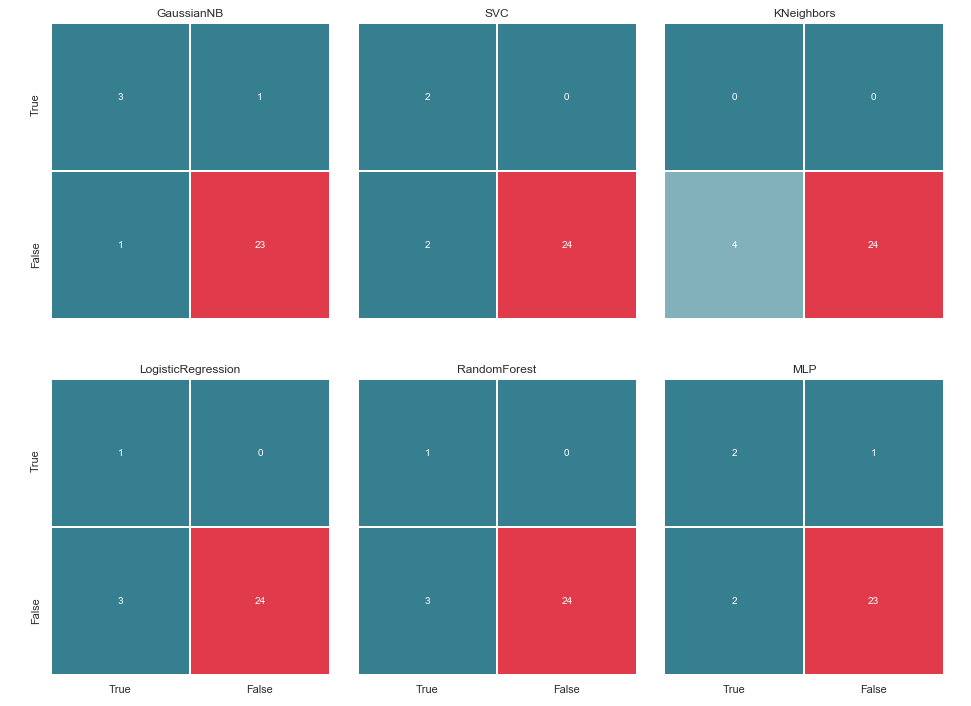
Antes de continuar, vale la pena dar algunas aclaraciones. La designación Verdadero, que se encuentra a la izquierda de la matriz de error de un clasificador particular, significa que el clasificador considera a la persona sospechosa, el valor Falso significa que la persona está fuera de toda sospecha. Del mismo modo, Verdadero y Falso en la parte inferior de la imagen nos da una situación real, que puede no coincidir con la decisión del clasificador.

Por ejemplo, vemos que las decisiones de KNeighbours con una precisión de predicción del 85,71% coincidieron con el estado real de las cosas cuando el clasificador incluyó a 24 personas, que estaban fuera de sospecha, en una lista similar. Pero 4 personas de la lista de sospechosos también se incluyeron en esta lista. Si este clasificador tomara decisiones, tal vez alguien podría haber evitado la corte.

Por lo tanto, las matrices de error son una muy buena herramienta para comprender qué salió mal con los problemas de clasificación. Su principal ventaja es la visibilidad y, por lo tanto, les atraemos.

Métricas

En términos generales, esto se puede ilustrar con la siguiente imagen:

¿Y qué es TP, TN, FP y algún tipo de FN en este caso?

$$$TP \ - \ verdadero positivo \ solución \\ TN \ - \ verdadero negativo \ solución \\ FP \ - \ falso positivo \ solución \\ FN \ - \ falso negativo \ solución$

En otras palabras, nos esforzamos por garantizar que las respuestas del clasificador y el estado real de las cosas coincidan. Es decir, para garantizar que todos los números se distribuyan entre las celdas TP y TN (soluciones verdaderas) y no caigan en FN y FP (soluciones falsas).

Y dado que estamos hablando de abreviaturas, es hora de recordar las métricas de precisión (Precisión) e integridad (Recuperación).

Si se aleja del registro formal, la precisión se puede expresar como:

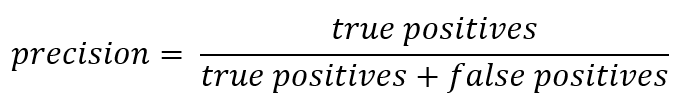
En otras palabras, se mantiene una cuenta de cuántas respuestas positivas recibidas del clasificador son correctas. Cuanto mayor sea la precisión, menor será el número de falsos aciertos (la precisión es 1 si no hubiera FP).

El retiro generalmente se presenta como:

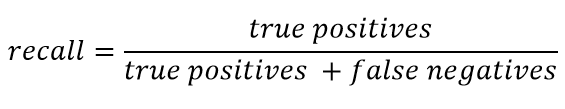
Recordar caracteriza la capacidad del clasificador de "adivinar" tantas respuestas positivas como sea posible. Cuanto mayor sea la integridad, menor será el FN.

Por lo general, intentan equilibrar entre los dos, pero en este caso la prioridad se dará por completo a Precision. La razón: un enfoque más humanista, el deseo de minimizar el número de falsos positivos y, como resultado, evitar la sospecha de inocentes.

Calculamos la precisión para nuestros clasificadores:

 from sklearn.metrics import precision_score def calculate_precision(X, y): result = pd.DataFrame(columns=['classifier', 'precision']) for clf in classifiers: predicted = clf.predict(X_test) precision = precision_score(y_test, predicted, average='macro') classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'precision': precision}, ignore_index=True) print('Precision is {precision} for {classifier_name}'.format(precision=round(precision,2), classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='precision', palette=cmap, data=result) calculate_precision(X_train, y_train) 

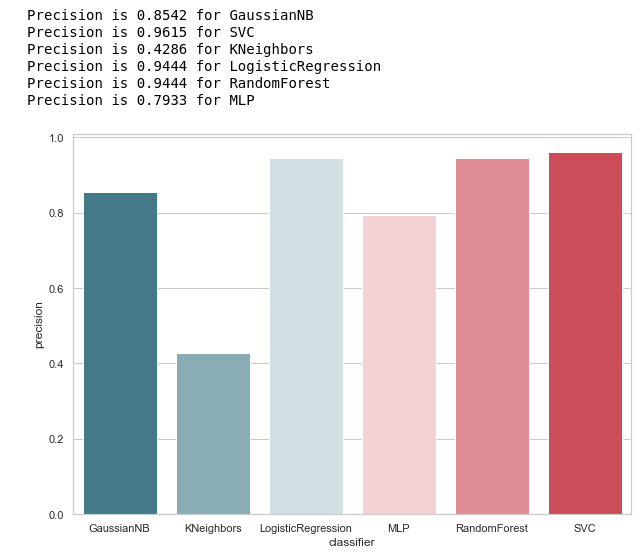
Como se desprende de la figura, salió como se esperaba: la precisión de KNeighbours resultó ser la más baja, porque el valor de TP es el más bajo.

Al mismo tiempo, hay un buen artículo sobre métricas sobre el Habré, y aquellos que quieran profundizar en este tema deben familiarizarse con él.

Selección de hiperparámetros

Después de encontrar la métrica que mejor se adapta a las condiciones seleccionadas (reducimos el número de FP), podemos volver a la primera pregunta: ¿Cuál es la razón de este comportamiento del clasificador KNeighbours?

La razón radica en la configuración predeterminada con la que se creó este modelo. Y, muy probablemente, muchos podrían exclamar a esta etapa: ¿por qué entrenar con los parámetros predeterminados? Existen herramientas de selección especiales, por ejemplo, el GridSearchCV de uso frecuente.
Sí, lo es, y ha llegado el momento de recurrir a él,

Pero antes de eso, eliminamos el clasificador bayesiano de nuestra lista. Permite un FP y, al mismo tiempo, este algoritmo no acepta ningún parámetro variable, por lo que el resultado no cambiará.

 classifiers.remove(gnb) 

Ajuste fino

Definimos una cuadrícula de parámetros para cada clasificador:

 parameters = {'SVC':{'kernel':('linear', 'rbf','poly'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'KNeighbors':{'algorithm':('ball_tree', 'kd_tree'), 'n_neighbors':[i for i in range(2,20)]}, 'LogisticRegression':{'penalty':('l1', 'l2'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'RandomForest':{'n_estimators':[i for i in range(10,101,10)],'random_state': (random_state,)}, 'MLP':{'activation':('relu','logistic'),'solver':('sgd','lbfgs'),'max_iter':(500,1000), 'hidden_layer_sizes':[(7,),(7,7)],'random_state': (random_state,)}} 

Además, quería prestar atención a la cantidad de capas / neuronas en MLP.
Se decidió establecerlos no mediante una búsqueda exhaustiva de todos los valores posibles, sino seguir basándose en la fórmula :

$$$N_h = \ frac {N_s} {(\ alpha * (N_i + N_o))} = \ frac {117} {(2 * (7 + 1))} \ aprox 7$

Quiero decir de inmediato, la capacitación y la validación cruzada se realizarán solo en la muestra de capacitación. Supongo que existe la opinión de que puede hacer esto en todos los datos, como en el ejemplo con Iris Dataset. Pero, en mi opinión, este enfoque no está completamente justificado, ya que no será posible confiar en los resultados de la verificación en una muestra de prueba.

Realizaremos la optimización y reemplazaremos nuestros clasificadores con su versión mejorada:

 from sklearn.model_selection import GridSearchCV warnings.filterwarnings('ignore') for idx,clf in enumerate(classifiers): classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') params = parameters.get(classifier) if not params: continue new_clf = clf.__class__() gs = GridSearchCV(new_clf, params, cv=5) result =gs.fit(X_train, y_train) print(f'The best params for {classifier} are {result.best_params_}') classifiers[idx] = result.best_estimator_ 

Después de elegir una métrica para la evaluación y realizar GridSearchCV, estamos listos para trazar la línea final.

Para resumir

Matriz de error v.2

 matrices = make_confussion_matrices(X_train,y_train) draw_confussion_matrices(1,2,first_row,figsize = (10.5,6)) draw_confussion_matrices(1,3,second_row,figsize = (16,6)) 

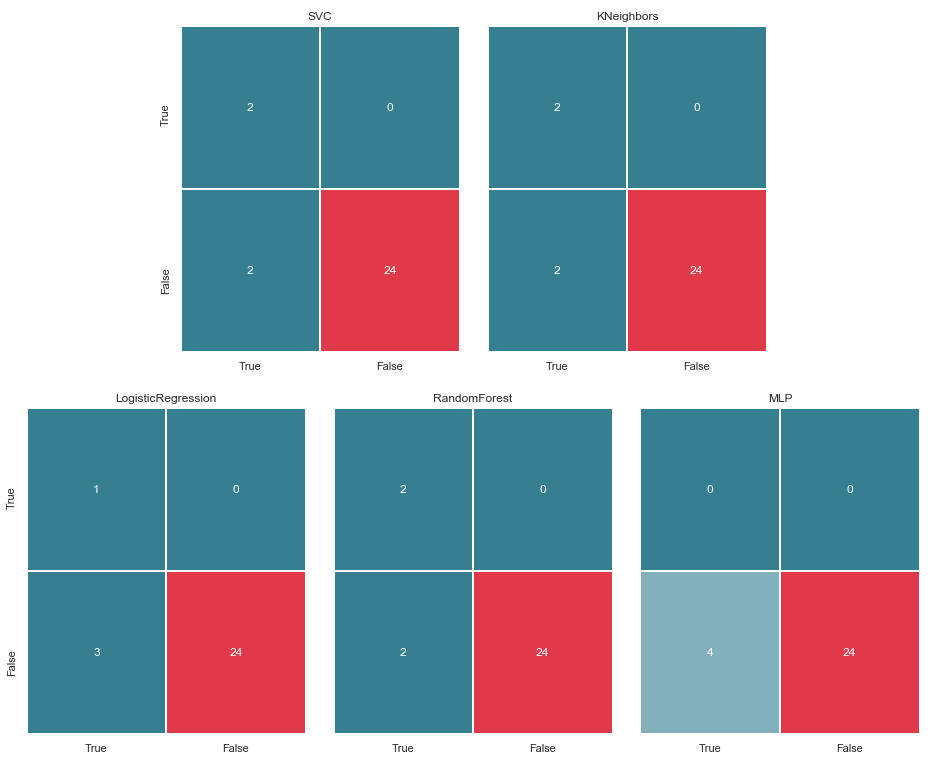
Como se puede ver en la matriz, MLP mostró degradación y consideró que no había sospechosos en la muestra de prueba. Random Forest ganó precisión y corrigió los parámetros para Falso negativo y Verdadero positivo. Y KNeighbours mostró una mejora en la predicción. El pronóstico para otros no ha cambiado.

Exactitud v.2

Ahora, ninguno de nuestros clasificadores actuales tiene errores con Falso Positivo, lo cual es una buena noticia. Pero, si expresamos todo en el idioma de los números, obtenemos la siguiente imagen:

 calculate_precision(X_train, y_train) 

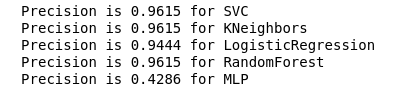
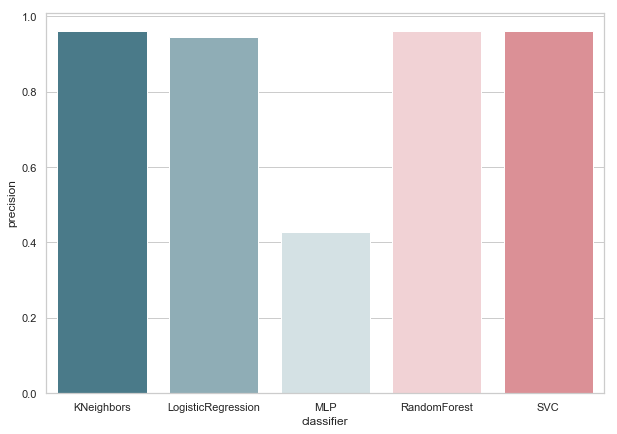
Se identificaron 3 clasificadores con la puntuación de precisión más alta. Y tienen los mismos valores, basados ​​en la matriz de error. ¿Qué clasificador elegir?

Quien es mejor

Me parece que esta es una pregunta bastante difícil para la que no hay una respuesta universal. Sin embargo, mi punto de vista en este caso se vería así:

1. El clasificador debe ser lo más simple posible en su implementación técnica. Entonces tendrá menos riesgo de reentrenamiento (probablemente esto sucedió con MLP). Por lo tanto, este no es el Bosque Aleatorio, ya que este algoritmo es un conjunto de 30 árboles y, como resultado, depende de ellos. En consonancia con una de las ideas de Python Zen: simple es mejor que complejo.

2. No está mal cuando el algoritmo era intuitivo. Es decir, KNeighbours se percibe de manera más simple que los SVM con potencial espacio multidimensional.
Lo que a su vez es similar a otra declaración: explícito es mejor que implícito.

Por lo tanto, KNeighbours con 3 vecinos, en mi opinión, es el mejor candidato.

Este es el final de la segunda parte, que describe el uso de Enron Dataset como un ejemplo de la tarea de clasificación en el aprendizaje automático. Basado en los materiales del curso de Introducción al aprendizaje automático sobre Udacity. También hay un cuaderno de Python que refleja toda la secuencia de acciones descrita.