Teoría de juegos: toma de decisiones con ejemplos en Kotlin

La teoría de juegos es una disciplina matemática que considera modelar las acciones de los jugadores que tienen un objetivo, que es elegir las estrategias óptimas para el comportamiento en un conflicto. En Habré, este tema ya se ha cubierto , pero hoy hablaremos sobre algunos de sus aspectos con más detalle y consideraremos ejemplos sobre Kotlin.

Entonces, una estrategia es un conjunto de reglas que determinan la elección de un curso de acción para cada movimiento personal, dependiendo de la situación. La estrategia óptima del jugador es la estrategia que asegura la mejor posición en un juego determinado, es decir. ganancia máxima Si el juego se repite varias veces y contiene, además de movimientos personales al azar, la estrategia óptima proporciona la ganancia máxima promedio.

La tarea de la teoría de juegos es identificar las estrategias óptimas para los jugadores. La suposición principal, en base a la cual se encuentran las estrategias óptimas, es que el oponente (u oponentes) no es menos inteligente que el propio jugador, y hace todo lo posible para lograr su objetivo. El cálculo de un oponente razonable es solo una de las posibles posiciones en el conflicto, pero en la teoría de los juegos es la base.

Hay juegos con la naturaleza en los que solo hay un participante que maximiza sus ganancias. Los juegos con la naturaleza son modelos matemáticos en los que la elección de la solución depende de la realidad objetiva. Por ejemplo, demanda del consumidor, estado de la naturaleza, etc. "Naturaleza" es un concepto generalizado de un adversario que no persigue sus propios objetivos. En este caso, se utilizan varios criterios para seleccionar la estrategia óptima.
Hay dos tipos de tareas en los juegos con la naturaleza:

1. la tarea de tomar decisiones en condiciones de riesgo cuando se conocen las probabilidades con las que la naturaleza acepta cada uno de los estados posibles;
2. tareas de toma de decisiones en condiciones de incertidumbre, cuando no es posible obtener información sobre las probabilidades de ocurrencia de estados de la naturaleza.

Brevemente sobre estos criterios se describe aquí .

Ahora consideraremos los criterios de toma de decisiones en estrategias puras, y al final del artículo resolveremos el juego en estrategias mixtas por el método analítico.

Declaración del problema.

Analizaremos todos los criterios de toma de decisiones utilizando un ejemplo directo. La tarea es esta: el agricultor necesita determinar en qué proporciones sembrar su campo con tres cultivos, si el rendimiento de estos cultivos y, por lo tanto, el beneficio, depende de cómo será el verano: fresco y lluvioso, normal o cálido y seco. El agricultor calculó el beneficio neto de 1 hectárea de diferentes cultivos según el clima. El juego está determinado por la siguiente matriz:



Además presentaremos esta matriz en forma de estrategias:

$$

$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$$

La estrategia óptima deseada se denota por $$$u_ {opt}$ . Resolveremos el juego utilizando los criterios de Wald, optimismo, pesimismo, Savage y Hurwitz en condiciones de incertidumbre y los criterios de Bayes y Laplace en condiciones de riesgo.

Como se mencionó anteriormente, los ejemplos estarán en Kotlin. Observo que, en general, existen soluciones como Gambit (escrito en C), Axelrod y PyNFG (escrito en Python), pero montaremos nuestra propia bicicleta, montada en la rodilla, solo para pinchar un poco con estilo, moda y lenguaje de programación juvenil.

Para implementar mediante programación la solución del juego, presentaremos varias clases. Primero, necesitamos una clase que nos permita describir una fila o columna de una matriz de juego. La clase es extremadamente simple y contiene una lista de posibles valores (alternativas o estados de la naturaleza) y su nombre correspondiente. El campo key se utilizará para la identificación, así como para la comparación, y será necesaria la comparación en la implementación de la dominación.


La matriz del juego contiene información sobre alternativas y estados de la naturaleza. Además, implementa algunos métodos, por ejemplo, encontrar el conjunto dominante y el precio neto del juego.


Describimos la interfaz que cumple con los criterios.

Toma de decisiones bajo incertidumbre

Tomar decisiones ante la incertidumbre sugiere que el oponente razonable no se opone al jugador.

Criterio de Wald

El criterio de Wald maximiza el peor resultado posible:

$$

$$u_ {opt} = max_ {i} min_ {j} [U]$$

Usar el criterio asegura contra el peor resultado, pero el precio de tal estrategia es la pérdida de la oportunidad de obtener el mejor resultado posible.

Considera un ejemplo. Para estrategias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encuentra los mínimos y obtén los siguientes tres $$$S = (0, 1, -1)$ . El máximo para el triple indicado será el valor 1, por lo tanto, de acuerdo con el criterio de Wald, la estrategia ganadora es la estrategia $$$U_ {2} = (2,3,1)$ correspondiente al cultivo de plantación 2.

La implementación del software del criterio de Wald es simple:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

En aras de la claridad, por primera vez mostraré cómo se vería la solución como una prueba:


Es fácil adivinar que para otros criterios, la diferencia solo estará en la creación del objeto de criteria .

Criterio de optimismo

Cuando se utiliza el criterio de un optimista, el jugador elige una solución que ofrezca el mejor resultado, mientras que el optimista supone que las condiciones del juego serán más favorables para él:

$$

$$u_ {opt} = max_ {i} max_ {j} [U]$$

La estrategia de un optimista puede tener consecuencias negativas cuando la oferta máxima coincide con la demanda mínima: la empresa puede recibir pérdidas al cancelar productos no vendidos. Al mismo tiempo, la estrategia del optimista tiene un cierto significado, por ejemplo, no necesita atender a clientes insatisfechos, ya que cualquier demanda posible siempre se satisface, por lo tanto, no es necesario mantener la ubicación de los clientes. Si se alcanza la máxima demanda, entonces la estrategia del optimista le permite obtener la máxima utilidad, mientras que otras estrategias conducirán a la pérdida de beneficios. Esto le da ciertas ventajas competitivas.

Considera un ejemplo. Para estrategias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encontrar, encontrar el máximo y obtener los siguientes tres $$$S = (5, 3, 4)$ . El máximo para el triple indicado será el valor 5, por lo tanto, según el criterio de optimismo, la estrategia ganadora es la estrategia $$$U_ {1} = (0.2.5)$ correspondiente al cultivo de plantación 1.

La implementación del criterio de optimismo casi no es diferente del criterio de Wald:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Criterio de pesimismo

Este criterio está destinado a seleccionar el elemento más pequeño de la matriz del juego de sus elementos mínimos posibles:

$$

$$u_ {opt} = min_ {i} min_ {j} [U]$$

El criterio del pesimismo sugiere que el desarrollo de los eventos será desfavorable para el tomador de decisiones. Al utilizar este criterio, el responsable de la toma de decisiones se guía por la posible pérdida de control sobre la situación, por lo tanto, trata de excluir los riesgos potenciales eligiendo la opción con una rentabilidad mínima.

Considera un ejemplo. Para estrategias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encontrar, encontrar el mínimo y obtener los siguientes tres $$$S = (0, 1, -1)$ . El mínimo para el triple indicado será el valor -1, por lo tanto, de acuerdo con el criterio de pesimismo, la estrategia ganadora es la estrategia $$$U_ {3} = (4.3, -1)$ correspondiente al cultivo de plantación 3.

Después de conocer los criterios y el optimismo de Wald, es fácil adivinar cómo se verá la clase del criterio de pesimismo:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } } 

Criterio salvaje

El criterio Salvaje (criterio de un pesimista arrepentido) implica minimizar las mayores ganancias perdidas, en otras palabras, minimizar el mayor arrepentimiento por las ganancias perdidas:

$$

$$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i, j} = (max \ begin {bmatrix} u_ {1, j} \\ u_ {2, j} \\. .. \\ u_ {n, j} \ end {bmatrix} - u_ {i, j})$$

En este caso, S es la matriz de los arrepentimientos.

La solución óptima según el criterio de Savage debería dar el menor pesar de los arrepentimientos encontrados en el paso anterior. La solución correspondiente a la utilidad encontrada será óptima.

Las características de la solución obtenida incluyen una ausencia garantizada de las mayores decepciones y una disminución garantizada en las ganancias máximas posibles de otros jugadores.

Considera un ejemplo. Para estrategias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ hacer una matriz de arrepentimientos:



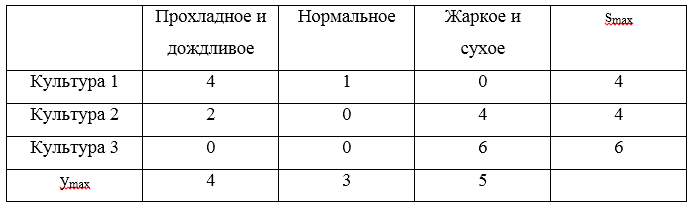
Tres arrepentimientos máximos $$$S = (4,4,6)$ . El valor mínimo de estos riesgos será un valor de 4, que corresponde a las estrategias. $$$U_ {1}$ y $$$U_ {2}$ .

Programar la prueba Savage es un poco más difícil:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } } 

Criterio de Hurwitz

El criterio de Hurwitz es un compromiso regulado entre el pesimismo extremo y el optimismo completo:

$$

$$u_ {opt} = max (\ gamma × A (k) + A (0) × (1 - \ gamma))$$

A (0) es la estrategia del pesimista extremo, A (k) es la estrategia del optimista completo, $$$\ gamma = 1$ - valor establecido del coeficiente de peso: $$$0 \ leq \ gamma \ leq1$ ; $$$\ gamma = 0$ - pesimismo extremo, $$$\ gamma = 1$ - Completo optimismo.

Con una pequeña cantidad de estrategias discretas, establecer el valor deseado del coeficiente de peso $$$\ gamma$ , y luego redondea el resultado al valor más cercano posible, teniendo en cuenta la discretización realizada.

Considera un ejemplo. Para estrategias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ . Suponemos que el coeficiente de optimismo $$$\ gamma = $ 0.$ . Ahora haz una tabla:



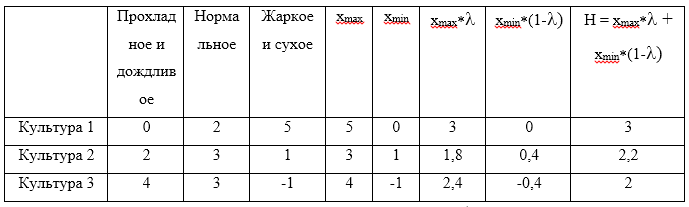
El valor máximo del H calculado será el valor 3, que corresponde a la estrategia. $$$U_ {1}$ .

La implementación del criterio de Hurwitz ya es más voluminosa:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } } 

Toma de decisiones en riesgo

Los métodos de toma de decisiones pueden basarse en criterios para la toma de decisiones en condiciones de riesgo, sujeto a las siguientes condiciones:

• falta de información confiable sobre las posibles consecuencias;
• la presencia de distribuciones de probabilidad;
• conocimiento de la probabilidad de resultados o consecuencias para cada decisión.

Si se toma una decisión en condiciones de riesgo, los costos de las decisiones alternativas se describen mediante distribuciones de probabilidad. En este sentido, la decisión se basa en el uso del criterio del valor esperado, según el cual se comparan soluciones alternativas en términos de maximizar las ganancias esperadas o minimizar los costos esperados.

El criterio del valor esperado se puede reducir para maximizar el beneficio esperado (promedio) o para minimizar los costos esperados. En este caso, se supone que el beneficio (costos) asociado con cada solución alternativa es una variable aleatoria.

La formulación de tales tareas suele ser la siguiente: una persona elige cualquier acción en una situación donde los eventos aleatorios influyen en el resultado de la acción. Pero el jugador tiene algún conocimiento sobre las probabilidades de estos eventos y puede calcular la combinación y secuencia más rentable de sus acciones.

Para continuar dando ejemplos, complementamos la matriz del juego con probabilidades:



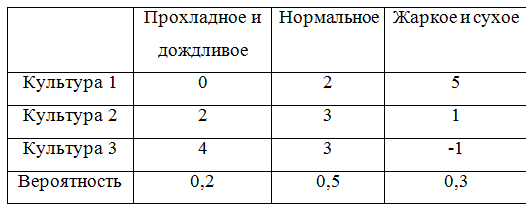
Para tener en cuenta las probabilidades, una clase que describa la matriz del juego tendrá que rehacerse ligeramente. Resultó, en verdad, no muy elegante, pero bueno.

Criterio de Bayes

El criterio de Bayes (criterio de expectativa) se utiliza en problemas de toma de decisiones en condiciones de riesgo como una evaluación de la estrategia $$$u_ {i}$ Aparece la expectativa matemática de la variable aleatoria correspondiente. De acuerdo con esta regla, la estrategia óptima del jugador $$$u_ {opt}$ se encuentra a partir de la condición:

$$

$$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i, j} \ cdot y_ {j} ^ 0$$

En otras palabras, un indicador de ineficiencia de la estrategia. $$$u_ {i}$ según el criterio de Bayes con respecto a los riesgos es el valor promedio (expectativa) de los riesgos de la i-ésima fila de la matriz $$$U$ cuyas probabilidades coinciden con las probabilidades de la naturaleza. Entonces lo óptimo entre las estrategias puras según el criterio de Bayes con respecto a los riesgos es la estrategia $$$u_ {opt}$ tener una ineficiencia mínima, es decir, un riesgo promedio mínimo. El criterio bayesiano es equivalente con respecto a las ganancias y relativo a los riesgos, es decir. si la estrategia $$$u_ {opt}$ es óptimo según el criterio de Bayes con respecto a las victorias, luego es óptimo según el criterio de Bayes con respecto a los riesgos, y viceversa.

Pasemos al ejemplo y calculemos las expectativas matemáticas:

$$

$$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0;$$

La expectativa matemática máxima es $$$M_1$ por lo tanto, una estrategia ganadora es una estrategia $$$U_1$ .

Implementación de software del criterio Bayes:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Criterio de Laplace

El criterio de Laplace presenta una maximización simplificada de la expectativa matemática de utilidad cuando el supuesto de niveles iguales de probabilidad de demanda es válido, lo que elimina la necesidad de recopilar estadísticas reales.

En general, cuando se utiliza el criterio de Laplace, la matriz de utilidades esperadas y el criterio óptimo se determinan de la siguiente manera:

$$

$$u_ {opt} = max [\ overline {U}] \\ \ overline {U} = \ begin {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix}, \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i, j }$$

Considere el ejemplo de la toma de decisiones según el criterio de Laplace. Calculamos la media aritmética para cada estrategia:

$$

$$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2.0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = $ 2.$$

Entonces la estrategia ganadora es la estrategia $$$U_1$ .

Implementación de software del criterio de Laplace:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Estrategias mixtas. Método analítico

El método analítico le permite resolver el juego en estrategias mixtas. Para formular un algoritmo para encontrar una solución a un juego mediante un método analítico, consideramos algunos conceptos adicionales.

Estrategia $$$U_ {i}$ domina la estrategia $$$U_ {i-1}$ si todo $$$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .En otras palabras, si en una fila de una matriz de pago todos los elementos son mayores o iguales que los elementos correspondientes de otra fila, entonces la primera fila domina a la segunda y se llama fila dominante. Y también si en alguna columna de la matriz de pago todos los elementos son menores o iguales que los elementos correspondientes de otra columna, entonces la primera columna domina a la segunda y se llama columna dominante.

El precio más bajo del juego se llama$$$\alpha = max_i min_j u_{ij}$ .
El precio más alto del juego se llama $$$\beta = min_j max_i u_{ij}$ .

Ahora puedes formular un algoritmo para resolver el juego por el método analítico:

1. Calcular fondo $$α y superior$\alpha$$$precios de los juegos β . Si$\beta$$$α = β , luego escriba la respuesta en estrategias puras; de lo contrario, continúe con la solución$\alpha = \beta$
2. Eliminar filas dominantes columnas dominantes. Puede haber varios. En su lugar en la estrategia óptima, los componentes correspondientes serán 0
3. Resuelve el juego matricial mediante programación lineal.

Para dar un ejemplo, debe dar una clase que describa la solución


Y la clase que realiza la solución por el método simplex. Como no entiendo las matemáticas, utilicé la implementación preparada de Apache Commons Math


Ahora ejecutamos la solución por el método analítico. Para mayor claridad, tomamos otra matriz de juego:

$$

$$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$$

Hay un conjunto dominante en esta matriz:
$$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$$

Solución de juego $$( 0 , 33 ; 0 , 67 ; 0 ) con el precio del juego igual a 3.33$(0,33; 0,67; 0)$

En lugar de una conclusión

Espero que este artículo sea útil para aquellos que necesitan una primera aproximación con la solución de los juegos con la naturaleza. En lugar de conclusiones, un enlace a GitHub .

Estaría agradecido por los comentarios constructivos!