Hola Habr! Les presento la portada de Solving multiarmed bandits: una comparación de epsilon-codicioso y Thompson .

El problema del bandido multi-armado

El problema del bandido multi-armado es una de las tareas más básicas en la ciencia de las soluciones. A saber, este es el problema de la asignación óptima de recursos en condiciones de incertidumbre. El nombre "bandido multi-armado" en sí proviene de máquinas tragamonedas antiguas controladas por manijas. Estos rifles de asalto fueron apodados "bandidos", porque después de hablar con ellos, la gente generalmente se sentía robada. Ahora imagine que hay varias máquinas de este tipo y la posibilidad de ganar contra diferentes autos es diferente. Desde que comenzamos a jugar con estas máquinas, queremos determinar qué posibilidad es mayor y usar esta máquina con más frecuencia que otras.

El problema es este: ¿cómo entendemos de manera más eficiente qué máquina es la más adecuada y, al mismo tiempo, probamos muchas funciones en tiempo real? Este no es un tipo de problema teórico, es un problema que una empresa enfrenta todo el tiempo. Por ejemplo, una empresa tiene varias opciones para los mensajes que deben mostrarse a los usuarios (por ejemplo, los mensajes incluyen anuncios, sitios, imágenes) para que los mensajes seleccionados maximicen una determinada tarea empresarial (conversión, clics, etc.)

Una forma típica de resolver este problema es ejecutar pruebas A / B muchas veces. Es decir, durante varias semanas para mostrar cada una de las opciones con la misma frecuencia, y luego, con base en pruebas estadísticas, decidir qué opción es mejor. Este método es adecuado cuando hay pocas opciones, digamos, 2 o 4. Pero cuando hay muchas opciones, este enfoque se vuelve ineficaz, tanto en tiempo perdido como en pérdida de ganancias.

El origen del tiempo perdido debería ser fácil de entender. Más opciones: se necesitan más pruebas A / B, se necesita más tiempo para tomar una decisión. La ocurrencia de ganancias perdidas no es tan obvia. Pérdida de oportunidad (costo de oportunidad): los costos asociados con el hecho de que en lugar de una acción realizamos otra, es decir, esto es lo que perdimos al invertir en A en lugar de B. Invertir en B es la ganancia perdida de invertir en A. Lo mismo con la comprobación de opciones. Las pruebas A / B no deben interrumpirse hasta que hayan terminado. Esto significa que el experimentador no sabe qué opción es mejor hasta que finalice la prueba. Sin embargo, todavía se cree que una opción será mejor que la otra. Esto significa que al prolongar las pruebas A / B, no mostramos las mejores opciones para un número suficientemente grande de visitantes (aunque no sabemos qué opciones no son las mejores), con lo que perdemos nuestras ganancias. Este es el beneficio perdido de las pruebas A / B. Si solo hay una prueba A / B, entonces tal vez la ganancia perdida no sea del todo grande. Una gran cantidad de pruebas A / B significa que durante mucho tiempo tenemos que mostrar a los clientes muchas de las mejores opciones. Sería mejor si pudiera descartar rápidamente las malas opciones en tiempo real, y solo entonces, cuando quedan pocas opciones, use las pruebas A / B para ellas.

Los muestreadores o agentes son formas de probar y optimizar rápidamente la distribución de opciones. En este artículo, le presentaré el muestreo de Thompson y sus propiedades. También compararé el muestreo de Thompson con el algoritmo de épsilon codicioso, otra opción popular para el problema de los bandidos con múltiples brazos. Todo se implementará en Python desde cero: todo el código se puede encontrar aquí .

Breve diccionario de conceptos

Agente, muestra, bandido ( agente, muestra, bandido ): un algoritmo que toma decisiones sobre qué opción mostrar.
Variante: una variante diferente del mensaje que ve el visitante.
Acción: la acción que ha elegido el algoritmo (qué opción mostrar).
Uso ( explotación ): elija maximizar la recompensa total en función de los datos disponibles.
Explore, explore : tome decisiones para comprender mejor el reembolso de cada opción.
Premio, puntos ( puntaje, recompensa ): una tarea empresarial, por ejemplo, conversión o clics. Por simplicidad, creemos que se distribuye binomialmente y es igual a 1 o 0 - clic o no.
Entorno, el contexto en el que opera el agente, opciones y su "recuperación" oculta para el usuario.
Retribución, probabilidad de éxito ( tasa de pago ): una variable oculta igual a la probabilidad de obtener una puntuación = 1, para cada opción es diferente. Pero el usuario no la ve.
Prueba ( prueba ): el usuario visita la página.
Lamentar es la diferencia entre cuál sería el mejor resultado de todas las opciones disponibles y cuál fue el resultado de la opción disponible en el intento actual. Cuanto menos se arrepientan de las acciones ya tomadas, mejor.
Mensaje ( mensaje ): un banner, una opción de página y más, diferentes versiones de las cuales queremos probar.
Muestreo: la generación de una muestra a partir de una distribución dada.

Explora y explota

Los agentes son algoritmos que buscan un enfoque para la toma de decisiones en tiempo real con el fin de lograr un equilibrio entre explorar el espacio de opciones y usar la mejor opción. Este equilibrio es muy importante. El espacio de opciones debe investigarse para tener una idea de qué opción es la mejor. Si descubrimos por primera vez esta opción óptima, y luego la usamos todo el tiempo, maximizaremos la recompensa total que nos ofrece el medio ambiente. Por otro lado, también queremos explorar otras opciones posibles: ¿qué pasaría si resultaran mejores en el futuro, pero todavía no lo sabemos? En otras palabras, queremos asegurarnos contra posibles pérdidas, tratando de experimentar un poco con opciones subóptimas para aclarar por sí mismos su recuperación. Si su recuperación es realmente mayor, se pueden mostrar con más frecuencia. Otra ventaja de investigar opciones es que podemos comprender mejor no solo la recuperación promedio, sino también la distribución aproximada de la recuperación, es decir, podemos estimar mejor la incertidumbre.
El principal problema, por lo tanto, es resolver: cuál es la mejor manera de salir del dilema entre exploración y explotación (compensación de exploración-explotación).

Algoritmo codicioso de Epsilon

Una forma típica de salir de este dilema es el algoritmo épsilon-codicioso. "Codicioso" significa exactamente lo que pensabas. Después de un período inicial, cuando accidentalmente hacemos intentos, digamos 1000 veces, el algoritmo elige ansiosamente la mejor opción k en el porcentaje de intentos. Por ejemplo, si e = 0.05, el algoritmo 95% del tiempo selecciona la mejor opción, y en el 5% restante selecciona intentos aleatorios. De hecho, este es un algoritmo bastante efectivo, sin embargo, puede que no sea suficiente para explorar el espacio de opciones, y por lo tanto, no será lo suficientemente bueno para evaluar qué opción es la mejor, para quedarse atascado en una opción subóptima. Vamos a mostrar en el código cómo funciona este algoritmo.

Pero primero, algunas dependencias. Debemos definir el entorno. Este es el contexto en el que se ejecutarán los algoritmos. En este caso, el contexto es muy simple. Llama al agente para que el agente decida qué acción elegir, luego el contexto lanza esta acción y devuelve los puntos recibidos por el agente (que de alguna manera actualiza su estado).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward

Los puntos se distribuyen binomialmente con probabilidad p dependiendo del número de la acción (así como podrían distribuirse continuamente, la esencia no habría cambiado). También definiré la clase BaseSampler: se necesita solo para almacenar registros y varios atributos.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

A continuación definimos 10 opciones y amortización para cada una. La mejor opción es la opción 9 con una recuperación de la inversión del 0,11%.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

Para tener algo sobre lo que construir, también definimos la clase RandomSampler. Esta clase es necesaria como modelo de referencia. Simplemente elige al azar una opción en cada intento y no actualiza sus parámetros.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

Otros modelos tienen la siguiente estructura. Todos tienen choose_k y métodos de actualización. choose_k implementa el método por el cual el agente selecciona una opción. actualizar actualiza los parámetros del agente: este método caracteriza cómo cambia la capacidad del agente para elegir la opción (con RandomSampler esta capacidad no cambia de ninguna manera). Ejecutamos el agente en el entorno utilizando el siguiente patrón.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs)

La esencia del algoritmo épsilon-codicioso es la siguiente.

Seleccione aleatoriamente k para n intentos.
En cada intento, para cada opción, evalúe las ganancias.
Después de todos los intentos n:
Con probabilidad 1 - e elija k con la ganancia más alta;
Con probabilidad e elija K al azar.

Código codicioso de Epsilon:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

A continuación, en el gráfico, puede ver los resultados de un muestreo puramente aleatorio, es decir, aquí no hay ningún modelo. El gráfico muestra qué elección realizó el algoritmo en cada intento, si hubo 10 mil intentos. El algoritmo solo lo intenta, pero no aprende. En total, anotó 418 puntos.

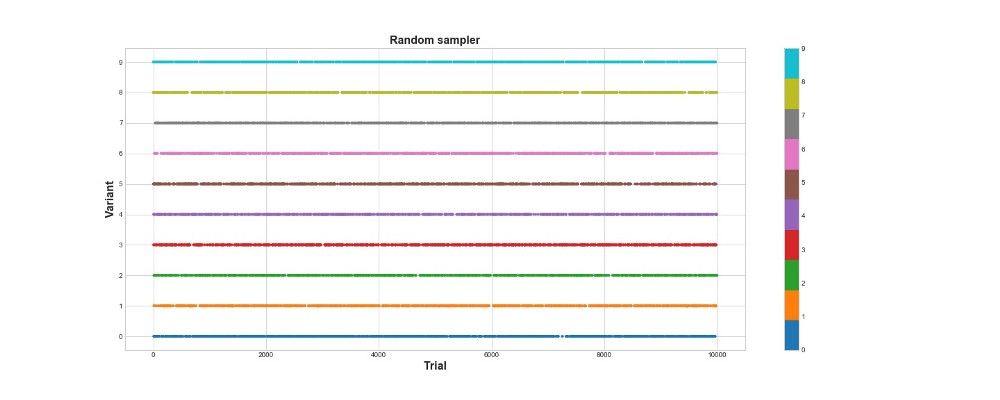
Veamos cómo se comporta el algoritmo épsilon-codicioso en el mismo entorno. Ejecute el algoritmo para 10 mil intentos con e = 0.1 y n_learning = 500 (el agente simplemente intenta los primeros 500 intentos, luego lo intenta con probabilidad e = 0.1). Vamos a evaluar el algoritmo de acuerdo con el número total de puntos que puntúa en el entorno.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg)

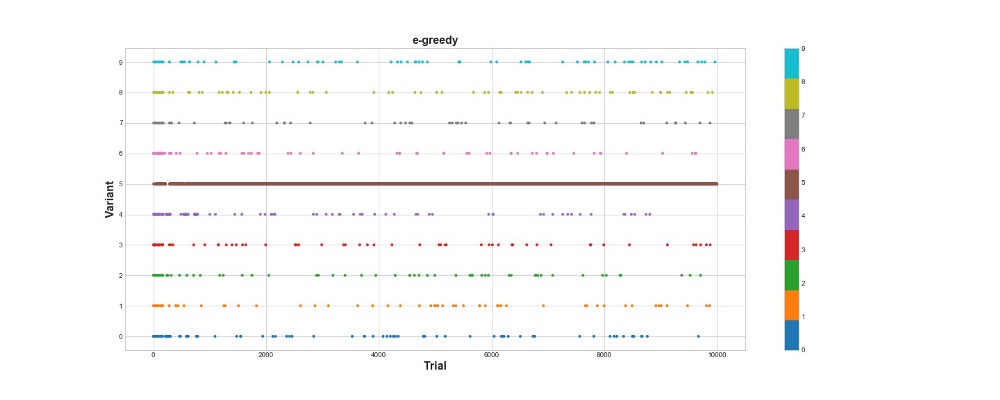
El algoritmo codicioso de Epsilon obtuvo 788 puntos, casi 2 veces mejor que el algoritmo aleatorio, ¡súper! El segundo gráfico explica este algoritmo bastante bien. Vemos que para los primeros 500 pasos las acciones se distribuyen aproximadamente de manera uniforme y K se elige al azar. Sin embargo, entonces comienza a explotar fuertemente la opción 5: esta es una opción bastante fuerte, pero no la mejor. También vemos que el agente todavía selecciona aleatoriamente el 10% del tiempo.

Esto es bastante bueno: escribimos solo unas pocas líneas de código, y ahora ya tenemos un algoritmo bastante poderoso que puede explorar el espacio de opciones y tomar decisiones cercanas a lo óptimo. Por otro lado, el algoritmo no encontró la mejor opción. Sí, podemos aumentar el número de pasos para aprender, pero de esta manera pasaremos aún más tiempo en una búsqueda aleatoria, empeorando aún más el resultado final. Además, la aleatoriedad se cose en este proceso de forma predeterminada; es posible que no se encuentre el mejor algoritmo.

Más tarde, ejecutaré cada uno de los algoritmos muchas veces para que podamos compararlos entre sí. Pero por ahora, echemos un vistazo al muestreo de Thompson y probémoslo en el mismo entorno.

Muestreo de Thompson

El muestreo de Thompson es fundamentalmente diferente del algoritmo de épsilon codicioso en tres puntos principales:

No es codicioso.
Hace intentos de una manera más sofisticada.
Es bayesiano.

El punto principal es el párrafo 3, los párrafos 1 y 2 se siguen de él.

La esencia del algoritmo es esta:

Establezca la distribución beta inicial entre 0 y 1 para el reembolso de cada opción.
Pruebe las opciones de esta distribución, seleccione el parámetro Theta máximo.
Elija la opción k que está asociada con la mayor theta.
Ver cuántos puntos se han puntuado, actualizar los parámetros de distribución.

Lea más sobre la distribución beta aquí .
Y sobre su uso en Python, aquí .

Código de algoritmo:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

La notación formal del algoritmo se ve así.

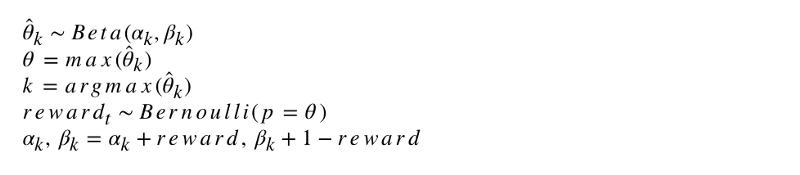
Programemos este algoritmo. Al igual que otros agentes, ThompsonSampler hereda de BaseSampler y define sus propios métodos choose_k y update. Ahora lanza nuestro nuevo agente.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa)

Como puede ver, obtuvo más puntajes que el algoritmo de épsilon codicioso. Genial Veamos el gráfico de la selección de intentos. Dos cosas interesantes son visibles en él. En primer lugar, el agente descubrió correctamente la mejor opción (opción 9) y la utilizó al máximo. En segundo lugar, el agente usó otras opciones, pero de una manera más complicada: después de aproximadamente 1000 intentos, el agente, además de la opción principal, utilizó principalmente las opciones más poderosas entre las demás. En otras palabras, no eligió al azar, sino de manera más competente.

¿Por qué funciona esto? Es simple: la incertidumbre en la distribución posterior de los beneficios esperados para cada opción significa que cada opción se selecciona con una probabilidad aproximadamente proporcional a su forma, determinada por los parámetros alfa y beta. En otras palabras, en cada intento, el muestreo de Thompson activa la opción de acuerdo con la probabilidad posterior de que tenga el beneficio máximo. En términos generales, teniendo en cuenta la información de distribución sobre la incertidumbre, el agente decide cuándo examinar el entorno y cuándo usar la información. Por ejemplo, una opción débil con alta incertidumbre posterior puede pagar más por este intento. Pero para la mayoría de los intentos, cuanto más fuerte es su distribución posterior, mayor es su promedio y menor es su desviación estándar, y por lo tanto, mayor es la posibilidad de elegirlo.

Otra propiedad notable del algoritmo de Thompson: dado que es bayesiano, podemos estimar la incertidumbre en la estimación de recuperación de la inversión para cada opción utilizando sus parámetros. El siguiente gráfico muestra distribuciones posteriores en 6 puntos diferentes y en 20,000 intentos. Verá cómo las distribuciones comienzan a converger gradualmente a la opción con la mejor recuperación de la inversión.

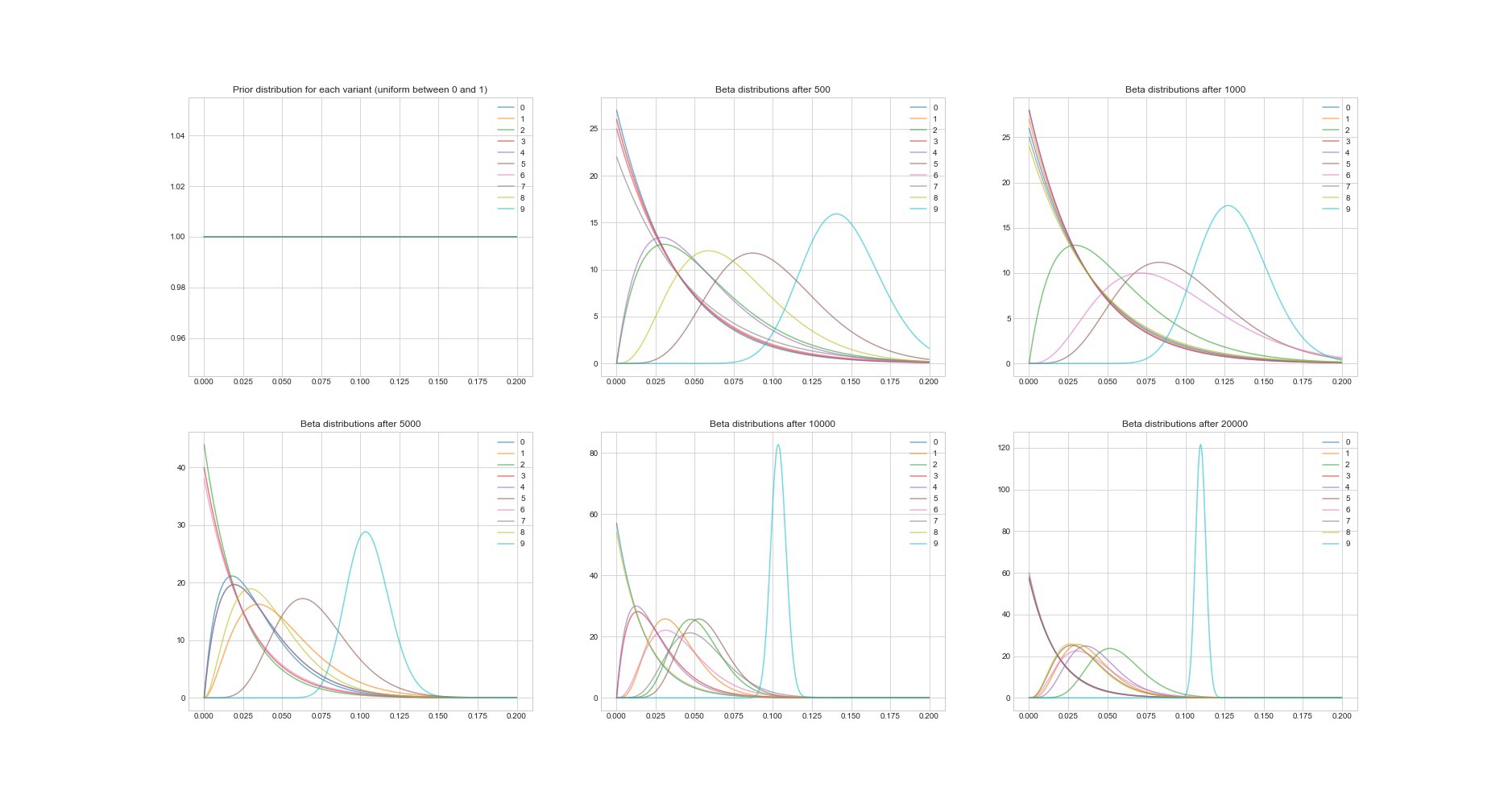
Ahora compare los 3 agentes en 100 simulaciones. 1 simulación es un lanzamiento de agente en 10,000 intentos.

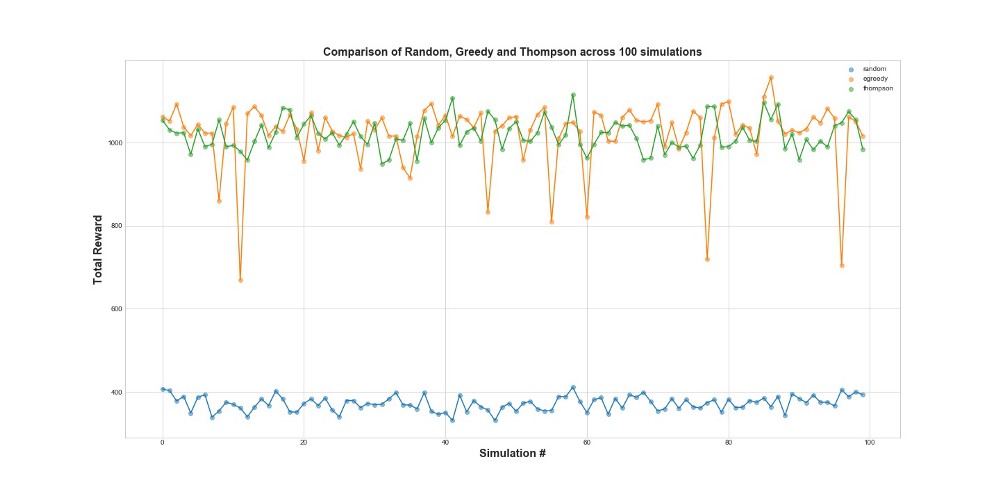
Como puede ver en el gráfico, tanto la estrategia de épsilon codicioso como el muestreo de Thompson funcionan mucho mejor que el muestreo aleatorio. Puede sorprenderle que la estrategia de épsilon codicioso y el muestreo de Thompson sean realmente comparables en términos de su rendimiento. La estrategia codiciosa de Epsilon puede ser muy efectiva, pero es más arriesgada, ya que puede atascarse en una opción subóptima; esto se puede ver en las fallas del gráfico. Pero el muestreo de Thompson no puede, porque hace la elección en el espacio de opciones de una manera más compleja.

Arrepentimiento

Otra forma de evaluar qué tan bien funciona el algoritmo es evaluar el arrepentimiento. En términos generales, cuanto más pequeño es, en relación con las acciones ya tomadas, mejor. A continuación se muestra un gráfico del arrepentimiento total y el arrepentimiento por el error. Una vez más, cuanto menos arrepentimiento, mejor.

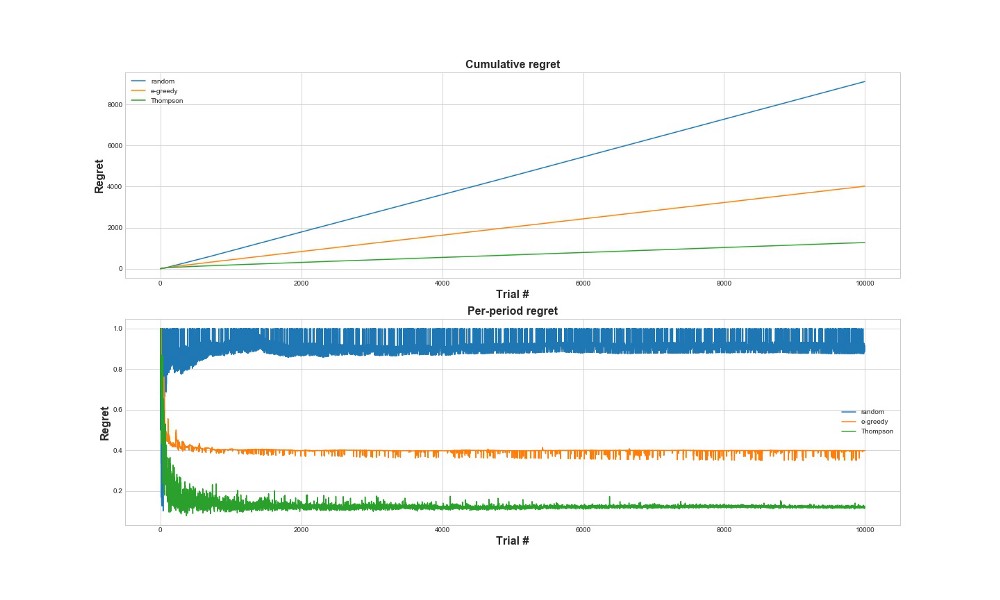
En el gráfico superior, vemos el arrepentimiento total, y en el arrepentimiento inferior el intento. Como se puede ver en los gráficos, el muestreo de Thompson converge a un arrepentimiento mínimo mucho más rápido que la estrategia de épsilon codicioso. Y converge a un nivel inferior. Con el muestreo de Thompson, el agente lamenta menos porque puede detectar mejor la mejor opción y probar mejor las opciones más prometedoras, por lo que el muestreo de Thompson es particularmente adecuado para casos de uso más avanzados, como modelos estadísticos o redes neuronales para elegir k.

Conclusiones

Esta es una publicación técnica bastante larga. Para resumir, podemos usar métodos de muestreo bastante sofisticados si tenemos muchas opciones que queremos probar en tiempo real. Una de las características muy buenas del muestreo de Thompson es que equilibra el uso y la exploración de una manera bastante complicada. Es decir, podemos permitirle optimizar la distribución de opciones de solución en tiempo real. Estos son algoritmos geniales, y deberían ser más útiles para un negocio que las pruebas A / B.

Importante! El muestreo de Thompson no significa que no necesite hacer pruebas A / B. Por lo general, primero encuentran las mejores opciones con su ayuda, y luego hacen pruebas A / B en ellas.

El problema de los bandidos con varios brazos: compare la estrategia codiciosa de Epsilon y el muestreo de Thompson