 Un recorrido completo de aprendizaje automático en Python: segunda parte
Un recorrido completo de aprendizaje automático en Python: segunda parteReunir todas las partes de un proyecto de aprendizaje automático puede ser complicado. En esta serie de artículos, revisaremos todas las etapas de la implementación del proceso de aprendizaje automático utilizando datos reales y descubriremos cómo se combinan entre sí las diversas técnicas.
En el
primer artículo, limpiamos y estructuramos los datos, realizamos un análisis exploratorio, recopilamos un conjunto de atributos para usar en el modelo y establecimos una línea de base para evaluar los resultados. Con la ayuda de este artículo, aprenderemos cómo implementar en Python y comparar varios modelos de aprendizaje automático, realizar ajustes hiperparamétricos para optimizar el mejor modelo y evaluar el rendimiento del modelo final en un conjunto de datos de prueba.
Todo el código del proyecto está
en GitHub , y
aquí está el segundo cuaderno relacionado con el artículo actual. ¡Puede usar y modificar el código como lo desee!
Evaluación y selección de modelos
Memo: Estamos trabajando en una tarea de regresión controlada, utilizando
la información energética de los edificios en Nueva York para crear un modelo que prediga qué
puntaje Energy Star recibirá
un edificio en particular. Estamos interesados tanto en la precisión del pronóstico como en la interpretabilidad del modelo.
Hoy puede elegir entre los
muchos modelos de aprendizaje automático disponibles , y esta abundancia puede ser intimidante. Por supuesto, hay
revisiones comparativas en la red que lo ayudarán a navegar al elegir un algoritmo, pero prefiero probar algunas en el trabajo y ver cuál es mejor. En su mayor parte, el aprendizaje automático se basa en resultados
empíricos en lugar de teóricos , y es casi
imposible comprender de antemano qué modelo es más preciso .
En general, se recomienda que comience con modelos simples e interpretables, como la regresión lineal, y si los resultados no son satisfactorios, continúe con métodos más complejos, pero generalmente más precisos. Este gráfico (muy anti-científico) muestra la relación entre la precisión e interpretabilidad de algunos algoritmos:
 Interpretabilidad y precisión ( Fuente ).
Interpretabilidad y precisión ( Fuente ).Evaluaremos cinco modelos de diversos grados de complejidad:
- Regresión lineal.
- El método de k-vecinos más cercanos.
- "Bosque al azar".
- Aumento de gradiente.
- Método de vectores de soporte.
Consideraremos no el aparato teórico de estos modelos, sino su implementación. Si le interesa la teoría, consulte
Introducción al aprendizaje estadístico (disponible de forma gratuita) o
Aprendizaje automático práctico con Scikit-Learn y TensorFlow . En ambos libros, la teoría se explica perfectamente y se muestra la efectividad del uso de los métodos mencionados en los lenguajes R y Python, respectivamente.
Rellene los valores faltantes
Aunque cuando borramos los datos, eliminamos las columnas en las que faltan más de la mitad de los valores, todavía tenemos muchos valores. Los modelos de aprendizaje automático no pueden funcionar con datos faltantes, por lo que debemos
completarlos .
Primero, consideramos los datos y recordamos cómo se ven:
import pandas as pd import numpy as np
Cada valor de
NaN es un registro faltante en los datos.
Puede completarlos de diferentes maneras , y utilizaremos el método de imputación mediana bastante simple, que reemplaza los datos faltantes con los valores promedio de las columnas correspondientes.
En el siguiente código, crearemos un
Imputer Scikit
-Learn Imputer con una estrategia mediana. Luego lo entrenamos en los datos de entrenamiento (usando
imputer.fit ), y lo aplicamos para completar los valores faltantes en los conjuntos de entrenamiento y prueba (usando
imputer.transform ). Es decir, los registros que faltan en los
datos de la
prueba se completarán con el valor medio correspondiente de los
datos de entrenamiento .
Hacemos el llenado y no entrenamos el modelo sobre los datos tal como están, para evitar el problema de la
fuga de datos de prueba cuando la información del conjunto de datos de prueba ingresa al entrenamiento.
Ahora todos los valores están llenos, no hay huecos.
Escalado de características
El escalado es el proceso general de cambiar el rango de una característica.
Este es un paso necesario , porque los signos se miden en diferentes unidades, lo que significa que cubren diferentes rangos. Esto distorsiona en gran medida los resultados de algoritmos tales como
el método del
vector de soporte y el método vecino k-más cercano, que tienen en cuenta las distancias entre las mediciones. Y el escalado le permite evitar esto. Aunque los métodos como
la regresión lineal y el "bosque aleatorio" no requieren la escala de las características, es mejor no descuidar este paso al comparar varios algoritmos.
Escalaremos usando cada atributo a un rango de 0 a 1. Tomamos todos los valores del atributo, seleccionamos el mínimo y lo dividimos por la diferencia entre el máximo y el mínimo (rango). Este método de escala a menudo se llama
normalización, y la otra forma principal es la estandarización .
Este proceso es fácil de implementar manualmente, por lo que utilizaremos el objeto
MinMaxScaler de Scikit-Learn. El código para este método es idéntico al código para completar los valores faltantes, solo se usa la escala en lugar de pegar. Recuerde que aprendemos el modelo solo en el conjunto de entrenamiento y luego transformamos todos los datos.
Ahora, cada atributo tiene un valor mínimo de 0 y un máximo de 1. Rellenar los valores faltantes y escalar los atributos: estas dos etapas son necesarias en casi cualquier proceso de aprendizaje automático.
Implementamos modelos de aprendizaje automático en Scikit-Learn
Después de todo el trabajo preparatorio, el proceso de creación, capacitación y ejecución de modelos es relativamente simple. Utilizaremos la biblioteca
Scikit-Learn en Python, que está bellamente documentada y con una sintaxis elaborada para construir modelos. Al aprender a crear un modelo en Scikit-Learn, puede implementar rápidamente todo tipo de algoritmos.
Ilustraremos el proceso de creación, capacitación (
.fit ) y prueba (
.predict ) usando el aumento de gradiente:
from sklearn.ensemble import GradientBoostingRegressor
Solo una línea de código para crear, entrenar y probar. Para construir otros modelos, usamos la misma sintaxis, cambiando solo el nombre del algoritmo.

Para evaluar los modelos objetivamente, calculamos el nivel base usando el valor medio de la meta y obtuvimos 24.5. Y los resultados fueron mucho mejores, por lo que nuestro problema puede resolverse mediante el aprendizaje automático.
En nuestro caso, el
aumento de gradiente (MAE = 10.013) resultó ser ligeramente mejor que el "bosque aleatorio" (10.014 MAE). Aunque estos resultados no pueden considerarse completamente honestos, porque para los hiperparámetros usamos principalmente los valores predeterminados. La efectividad de los modelos depende en gran medida de estos ajustes,
especialmente en el método del vector de soporte . Sin embargo, en función de estos resultados, elegiremos el aumento de gradiente y comenzaremos a optimizarlo.
Optimización del modelo hiperparamétrico.
Después de elegir un modelo, puede optimizarlo para la tarea a resolver ajustando los hiperparámetros.
Pero antes que nada, comprendamos
qué son los hiperparámetros y cómo se diferencian de los parámetros ordinarios .
- Los hiperparámetros del modelo pueden considerarse la configuración del algoritmo, que establecemos antes del inicio de su entrenamiento. Por ejemplo, el hiperparámetro es el número de árboles en el "bosque aleatorio", o el número de vecinos en el método k-vecinos más cercanos.
- Parámetros del modelo: lo que aprende durante el entrenamiento, por ejemplo, pesos en regresión lineal.
Al controlar el hiperparámetro, influimos en los resultados del modelo, cambiando el equilibrio entre su
subeducación y su reentrenamiento . El aprendizaje insuficiente es una situación en la que el modelo no es lo suficientemente complejo (tiene muy pocos grados de libertad) para estudiar la correspondencia de signos y objetivos. Un modelo poco entrenado tiene un
alto sesgo, que puede corregirse complicando el modelo.
La reentrenamiento es una situación en la que el modelo recuerda esencialmente los datos de entrenamiento. El modelo reentrenado tiene una
alta varianza, que se puede ajustar limitando la complejidad del modelo a través de la regularización. Los modelos poco entrenados y reentrenados no podrán generalizar bien los datos de prueba.
La dificultad para elegir los hiperparámetros correctos es que para cada tarea habrá un conjunto óptimo único. Por lo tanto, la única forma de elegir la mejor configuración es probar diferentes combinaciones en el nuevo conjunto de datos. Afortunadamente, Scikit-Learn tiene una serie de métodos que le permiten evaluar con eficacia los hiperparámetros. Además, proyectos como
TPOT intentan optimizar la búsqueda de hiperparámetros utilizando enfoques como
la programación genética . En este artículo, nos limitamos a usar Scikit-Learn.
Búsqueda aleatoria de verificación cruzada
Implementemos un método de ajuste de hiperparámetros llamado búsquedas aleatorias de validación cruzada:
- Búsqueda aleatoria : una técnica para seleccionar hiperparámetros. Definimos una cuadrícula y luego seleccionamos al azar varias combinaciones de ella, en contraste con la búsqueda de cuadrícula, en la que probamos sucesivamente cada combinación. Por cierto, la búsqueda aleatoria funciona casi tan bien como la búsqueda de cuadrícula , pero mucho más rápido.
- La verificación cruzada es una forma de evaluar la combinación seleccionada de hiperparámetros. En lugar de dividir los datos en conjuntos de entrenamiento y prueba, lo que reduce la cantidad de datos disponibles para el entrenamiento, utilizaremos la validación cruzada de bloque k (validación cruzada de plegado en K). Para hacer esto, dividiremos los datos de entrenamiento en k bloques, y luego ejecutaremos el proceso iterativo, durante el cual primero entrenaremos el modelo en bloques k-1, y luego compararemos el resultado al aprender en el bloque k-ésimo. Repetiremos el proceso k veces, y al final obtendremos el valor de error promedio para cada iteración. Esta será la evaluación final.
Aquí hay una ilustración gráfica de la validación cruzada de bloque k en k = 5:

Todo el proceso de búsqueda aleatoria de validación cruzada se ve así:
- Establecemos una cuadrícula de hiperparámetros.
- Seleccione aleatoriamente una combinación de hiperparámetros.
- Crea un modelo usando esta combinación.
- Evaluamos el resultado del modelo utilizando la validación cruzada de bloque k.
- Decidimos qué hiperparámetros dan el mejor resultado.
¡Por supuesto, todo esto no se hace manualmente, sino que usa
RandomizedSearchCV de Scikit-Learn!
Utilizaremos un modelo de regresión basado en el aumento de gradiente. Este es un método colectivo, es decir, el modelo consiste en numerosos "estudiantes débiles", en este caso, de árboles de decisión separados. Si los estudiantes aprenden en
algoritmos paralelos
como "bosque aleatorio" , y luego el resultado de la predicción se selecciona mediante votación, entonces en los
algoritmos de impulso como el aumento de gradiente, los estudiantes reciben capacitación secuencial y cada uno de ellos se "enfoca" en los errores cometidos por los predecesores.
En los últimos años, los algoritmos de refuerzo se han vuelto populares y, a menudo, ganan en competencias de aprendizaje automático.
El aumento de gradiente es una de las implementaciones en las que se utiliza Gradient Descent para minimizar el costo de la función. La implementación del aumento de gradiente en Scikit-Learn no se considera tan efectiva como en otras bibliotecas, por ejemplo, en
XGBoost , pero funciona bien en pequeños conjuntos de datos y proporciona pronósticos bastante precisos.
Volver a la configuración hiperparamétrica
En la regresión que usa el aumento de gradiente, hay muchos hiperparámetros que deben configurarse, para obtener más detalles, le remito a la documentación de Scikit-Learn. Optimizaremos:
loss : minimización de la función de pérdida;n_estimators : el número de árboles de decisión débiles utilizados (árboles de decisión);max_depth : profundidad máxima de cada árbol de decisión;min_samples_leaf : el número mínimo de ejemplos que deberían estar en el nodo hoja del árbol de decisión;min_samples_split : la cantidad mínima de ejemplos necesarios para dividir el nodo del árbol de decisión;max_features : el número máximo de características que se utilizan para separar nodos.
No estoy seguro de si alguien realmente comprende cómo funciona todo, y la única forma de encontrar la mejor combinación es probar diferentes opciones.
En este código, creamos una cuadrícula de hiperparámetros, luego creamos un objeto
RandomizedSearchCV y buscamos mediante la validación cruzada de 4 bloques para 25 combinaciones diferentes de hiperparámetros:
Puede usar estos resultados para una búsqueda de cuadrícula seleccionando parámetros para la cuadrícula que estén cerca de estos valores óptimos. Pero es poco probable que un ajuste adicional mejore significativamente el modelo. Hay una regla general: la construcción competente de características tendrá un impacto mucho mayor en la precisión del modelo que la configuración de hiperparámetro más costosa. Esta es la
ley de la disminución de la rentabilidad en relación con el aprendizaje automático : el diseño de atributos proporciona el mayor rendimiento, y el ajuste hiperparamétrico solo ofrece beneficios modestos.
Para cambiar el número de estimadores (árboles de decisión) mientras se conservan los valores de otros hiperparámetros, se puede realizar un experimento que demuestre el papel de esta configuración. La implementación se da
aquí , pero aquí está el resultado:
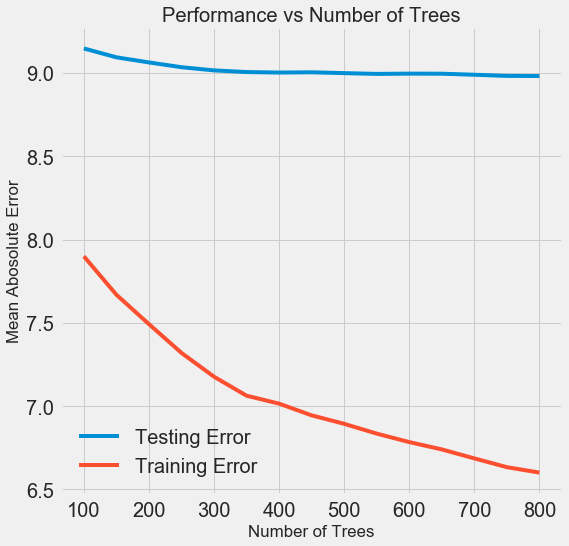
A medida que aumenta el número de árboles utilizados por el modelo, disminuye el nivel de errores durante el entrenamiento y las pruebas. Pero los errores de aprendizaje disminuyen mucho más rápido y, como resultado, el modelo se vuelve a entrenar: muestra excelentes resultados en los datos de entrenamiento, pero funciona peor en los datos de las pruebas.
En los datos de la prueba, la precisión siempre disminuye (porque el modelo ve las respuestas correctas para el conjunto de datos de entrenamiento), pero una caída significativa
indica una nueva capacitación. Este problema se puede resolver aumentando la cantidad de datos de entrenamiento o
reduciendo la complejidad del modelo utilizando hiperparámetros . Aquí no tocaremos los hiperparámetros, pero le recomiendo que siempre preste atención al problema del reciclaje.
Para nuestro modelo final, tomaremos 800 evaluadores, porque esto nos dará el nivel más bajo de error en la validación cruzada. ¡Ahora prueba el modelo!
Evaluación utilizando datos de prueba
Como personas responsables, nos aseguramos de que nuestro modelo de ninguna manera obtuviera acceso a los datos de las pruebas durante la capacitación. Por
lo tanto,
podemos usar la precisión cuando trabajamos con datos de prueba como un indicador de calidad del modelo cuando se admite en tareas reales.
Alimentamos los datos de prueba del modelo y calculamos el error. Aquí hay una comparación de los resultados del algoritmo de aumento de gradiente predeterminado y nuestro modelo personalizado:
El ajuste hiperparamétrico ayudó a mejorar la precisión del modelo en aproximadamente un 10%. Dependiendo de la situación, esto puede ser una mejora muy significativa, pero lleva mucho tiempo.
Puede comparar el tiempo de entrenamiento para ambos modelos usando el
%timeit magic
%timeit en Jupyter Notebooks. Primero, mida la duración predeterminada del modelo:
%%timeit -n 1 -r 5 default_model.fit(X, y) 1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
Un segundo para estudiar es muy decente. Pero el modelo ajustado no es tan rápido:
%%timeit -n 1 -r 5 final_model.fit(X, y) 12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)
Esta situación ilustra el aspecto fundamental del aprendizaje automático:
se trata de compromisos . Es constantemente necesario elegir un equilibrio entre precisión e interpretabilidad, entre
desplazamiento y dispersión , entre precisión y tiempo de operación, etc. La combinación correcta está completamente determinada por la tarea específica. En nuestro caso, un aumento de 12 veces en la duración del trabajo en términos relativos es grande, pero en términos absolutos es insignificante.
Obtuvimos los resultados finales del pronóstico, ahora analicémoslos y descubramos si hay desviaciones notables. A la izquierda hay un gráfico de la densidad de los valores predichos y reales, a la derecha hay un histograma del error:
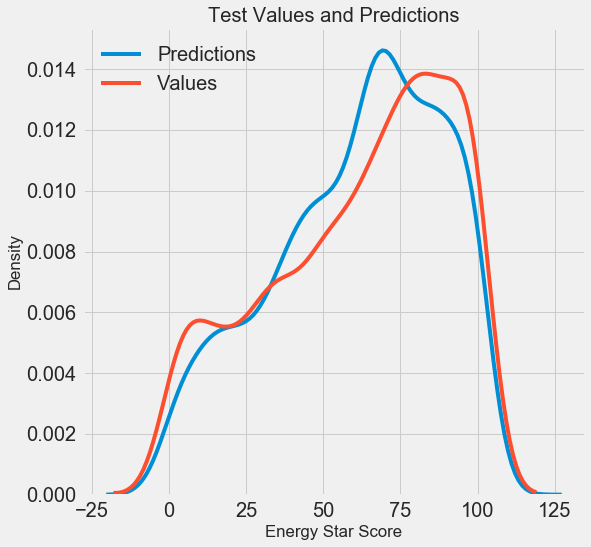

El pronóstico del modelo repite bien la distribución de los valores reales, mientras que en los datos de entrenamiento, el pico de densidad se ubica más cerca del valor medio (66) que del pico de densidad real (aproximadamente 100). Los errores tienen una distribución casi normal, aunque hay varios valores negativos grandes cuando el pronóstico del modelo es muy diferente de los datos reales. En el próximo artículo, examinaremos con más detalle la interpretación de los resultados.
Conclusión
En este artículo, examinamos varias etapas para resolver el problema del aprendizaje automático:
- Relleno de valores faltantes y funciones de escala.
- Evaluación y comparación de los resultados de varios modelos.
- Ajuste hiperparamétrico mediante búsqueda aleatoria de cuadrícula y validación cruzada.
- Evaluación del mejor modelo utilizando datos de prueba.
Los resultados indican que podemos utilizar el aprendizaje automático para predecir el puntaje Energy Star basado en las estadísticas disponibles. Con la ayuda del aumento de gradiente, se logró un error de 9.1 en los datos de prueba. El ajuste hiperparamétrico puede mejorar en gran medida los resultados, pero a costa de una desaceleración significativa. Esta es una de las muchas compensaciones a considerar en el aprendizaje automático.
En el próximo artículo, intentaremos descubrir cómo funciona nuestro modelo. También veremos los principales factores que influyen en el Energy Star Score. Si sabemos que el modelo es preciso, intentaremos comprender por qué predice de esta manera y qué nos dice sobre el problema en sí.