Solución simbólica de ecuaciones diferenciales lineales y sistemas mediante el método de transformación de Laplace utilizando SymPy

La implementación de algoritmos en Python usando cálculos simbólicos es muy conveniente para resolver problemas de modelado matemático de objetos definidos por ecuaciones diferenciales. Para resolver tales ecuaciones, las transformadas de Laplace se usan ampliamente, lo que, en términos simplificados, permite reducir el problema a la resolución de ecuaciones algebraicas simples.

En esta publicación, propongo considerar las funciones de las transformadas directas e inversas de Laplace de la biblioteca SymPy, que le permiten utilizar el método de Laplace para resolver ecuaciones y sistemas diferenciales usando Python.

El método de Laplace en sí y sus ventajas en la resolución de ecuaciones diferenciales lineales y sistemas están ampliamente cubiertos en la literatura, por ejemplo, en la publicación popular [1]. En el libro, el método de Laplace se presenta para su implementación en paquetes de software con licencia Mathematica, Maple y MATLAB (que implica la compra de este software por parte de una institución educativa) utilizando ejemplos seleccionados por el autor.

Hoy trataremos de considerar no un ejemplo separado de resolver un problema de aprendizaje usando Python, sino un método general para resolver ecuaciones diferenciales lineales y sistemas usando las funciones de transformadas de Laplace directas e inversas. Al mismo tiempo, ahorraremos un momento de aprendizaje: el lado izquierdo de la ecuación diferencial lineal con condiciones de Cauchy será formado por el propio alumno, y la parte rutinaria de la tarea, que consiste en la transformación directa de Laplace del lado derecho de la ecuación, se realizará utilizando la función laplace_transform () .

La historia de la autoría de la transformación de Laplace

Las transformaciones de Laplace (imágenes de Laplace) tienen una historia interesante. Por primera vez, la integral en la definición de la transformación de Laplace apareció en una de las obras de L. Euler. Sin embargo, generalmente se acepta en matemáticas llamar a una metodología o teorema el nombre del matemático que lo descubrió después de Euler. De lo contrario, habría varios cientos de teoremas diferentes de Euler.

En este caso, el siguiente después de Euler fue el matemático francés Pierre Simon de Laplace (Pierre Simon de Laplace (1749-1827)). Fue él quien utilizó tales integrales en su trabajo sobre la teoría de la probabilidad. El propio Laplace no aplicó los llamados "métodos operativos" para encontrar soluciones de ecuaciones diferenciales basadas en transformadas de Laplace (imágenes de Laplace). Estos métodos fueron descubiertos y popularizados por ingenieros prácticos, especialmente el ingeniero eléctrico inglés Oliver Heaviside (1850-1925). Mucho antes de que se probara rigurosamente la validez de estos métodos, el cálculo operativo se utilizó con éxito y ampliamente, aunque su legitimidad fue cuestionada en gran medida incluso a principios del siglo XX, y hubo un debate muy feroz sobre este tema.

Funciones de la transformada de Laplace directa e inversa.

1. Función de transformación directa de Laplace:
   sympy.integrals.transforms. laplace_transform (t, s, ** sugerencias).
   La función laplace_transform () realiza las transformadas de Laplace de la función f (t) de la variable real en la función F (s) de la variable compleja, de modo que:
   

   $$

   $$F (s) = \ int_ {0} ^ {∞} f (t) e ^ {- st} dt.$$
   
   Esta función devuelve (F, a, cond) , donde F (s) es la transformada de Laplace de la función f (t) , a <Re (s) es el semiplano donde se define F (s) , y cond son condiciones auxiliares para la convergencia de la integral.
   Si la integral no se puede calcular en forma cerrada, esta función devuelve un objeto LaplaceTransform no computarizado .
   Si configura la opción noconds = True , la función solo devuelve F (s) .
2. Función de transformación inversa de Laplace:
   
   sympy.integrals.transforms. inverse_laplace_transform (F, s, t, plane = None, ** pistas).
   
   La función inverse_laplace_transform () realiza la transformación inversa de Laplace de la función de la variable compleja F (s) en la función f (t) de la variable real, de modo que:
   

   $$

   $$f (t) = \ frac {1} {2 \ pi i} \ int_ {c-∞ \ cdot i} ^ {c + ∞ \ cdot i} e ^ {st} F (s) ds.$$
   
   Si la integral no se puede calcular en forma cerrada, esta función devuelve un objeto InverseLaplaceTransform sin calcular .
   

La transformación inversa de Laplace en el ejemplo de determinar las características de transición de los reguladores

La función de transferencia del controlador PID tiene la forma [2]:

$$

$$W (s) = (1+ \ frac {K_ {d} \ cdot T_ {d} \ cdot s} {1 + T_ {d} \ cdot s}) \ cdot K_ {p} \ cdot (1+ \ frac {1} {T_ {i} \ cdot s}) \ cdot \ frac {1} {s}.$$

Escribiremos un programa para obtener ecuaciones para las características transitorias de los controladores PID y PI para la función de transferencia reducida, y adicionalmente derivaremos el tiempo dedicado a la transformación visual inversa de Laplace.


Obtenemos:

Tiempo de transformación de Laplace visual inversa: 2,68 s



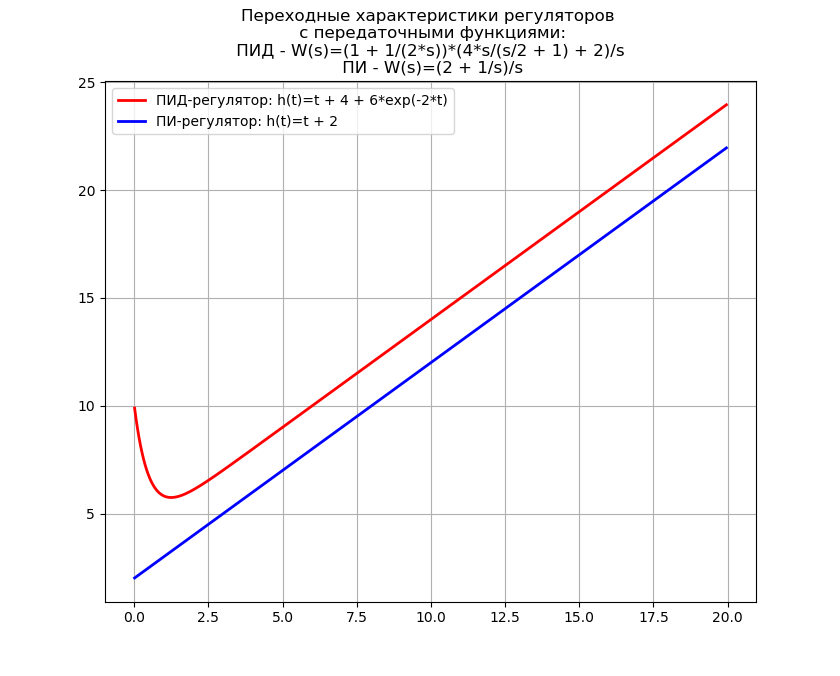
La transformación inversa de Laplace se usa a menudo en la síntesis de armas autopropulsadas, donde Python puede reemplazar costosos "monstruos" de software como MathCAD, por lo que el uso anterior de la transformación inversa es de importancia práctica.

Transformada de Laplace a partir de derivados de órdenes superiores para resolver el problema de Cauchy

Nuestra discusión continuará con la aplicación de transformadas de Laplace (imágenes de Laplace) para la búsqueda de soluciones de una ecuación diferencial lineal con coeficientes constantes de la forma:

$$

$$a \ cdot x '' (t) + b \ cdot x '(t) + c \ cdot x (t) = f (t). (1)$$

Si ayb son constantes, entonces

$$

$$L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ right \} (2)$$

para todos los s de manera que existan transformaciones de Laplace (imagen de Laplace) de las funciones f (t) y q (t) .

Verifiquemos la linealidad de las transformadas directas e inversas de Laplace utilizando las funciones previamente consideradas laplace_transform () e inverse_laplace_transform () . Para esto, tomamos f (t) = sin (3t) , q (t) = cos (7t) , a = 5 , b = 7 como ejemplo, y usamos el siguiente programa.


Obtenemos:

(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
Cierto
5 * sin (3 * t) + 7 * cos (7 * t)
5 * sin (3 * t) + 7 * cos (7 * t)

El código anterior también demuestra la unicidad de la transformación inversa de Laplace.

Suponiendo que $$$q (t) = f '(t)$ satisface las condiciones del primer teorema, luego de este teorema se deducirá que:

$$

$$L \ left \ {f '' (t) \ right \} = L \ left \ {q '(t) \ right \} = sL \ left \ {q (t) \ right \} - q (0) = sL \ left \ {f '(t) \ right \} - f' (0) = s \ left [sL \ left \ {f (t) -f (0) \ right \} \ right],$$

y asi

$$

$$L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).$$

Repetir este cálculo da

$$

$$L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).$$

Después de un número finito de tales pasos, obtenemos la siguiente generalización del primer teorema:

$$

$$L \ left \ {f ^ {(n)} (t) \ right \} = s ^ {n} L \ left \ {f (t) \ right \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =$$

$$

$$= s ^ {n} F (s) -s ^ {n-1} f (0) - \ cdot \ cdot \ cdot -sf ^ {(n-2)} (0) -f ^ {(n- 1)} (0). (3)$$

Aplicando la relación (3) que contiene los derivados transformados de Laplace de la función deseada con las condiciones iniciales de la ecuación (1), podemos obtener su solución de acuerdo con el método especialmente desarrollado en nuestro departamento con el apoyo activo de Scorobey para la biblioteca SymPy.

Un método para resolver ecuaciones diferenciales lineales y sistemas de ecuaciones basados ​​en transformadas de Laplace utilizando la biblioteca SymPy

Para demostrar el método, utilizamos una ecuación diferencial simple que describe el movimiento de un sistema que consiste en un punto material de una masa dada, montado en un resorte al que se aplica una fuerza externa. La ecuación diferencial y las condiciones iniciales para dicho sistema tienen la forma:

$$

$$x '' + 4x = \ sin (3t); x (0) = 1.2; x '(0) = 1, (4)$$

donde $$$x (0)$ - posición inicial reducida de la masa, $$$x '(0)$ - Velocidad de masa inicial reducida.

Un modelo físico simplificado definido por la ecuación (4) con condiciones iniciales distintas de cero [1]:



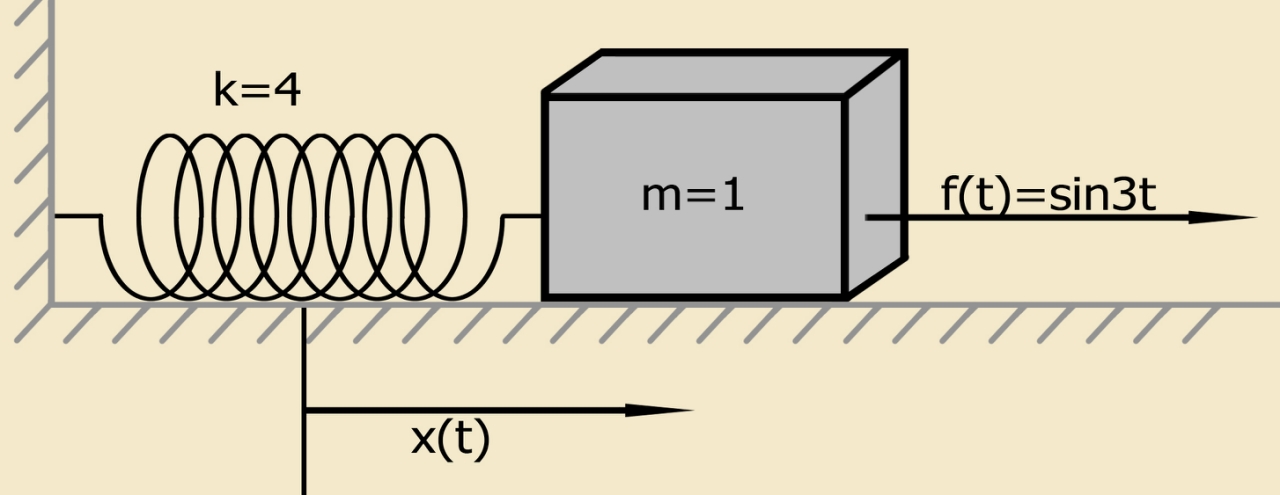
Un sistema que consiste en un punto material de una masa dada fijada en un resorte satisface el problema de Cauchy (un problema con las condiciones iniciales). El punto material de una masa dada está inicialmente en reposo en su posición de equilibrio.

Para resolver esta y otras ecuaciones diferenciales lineales mediante el método de transformación de Laplace, es conveniente utilizar el siguiente sistema obtenido de las relaciones (3):
$$$L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),$
$$$L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),$
$$$L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),$
$$$L \ left \ {f ^ {I} (t) \ right \} = s \ cdot F (s) -f (0), L \ left \ {f (t) \ right \} = F (s) .$
$$$L \ left \ {f (t) \ right \} = F (s). (5)$

La secuencia de soluciones que usan SymPy es la siguiente:

1. cargar los módulos necesarios y definir explícitamente variables simbólicas:
   
   

    from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function) 

   
   
2. Especifique la versión de la biblioteca Sympy para tener en cuenta sus características. Para hacer esto, ingrese las siguientes líneas:
   
   

    import SymPy print ('  sympy – %' % (sympy._version_)) 

   
   
3. Según el significado físico del problema, la variable de tiempo se determina para una región que incluye cero y números positivos. Establecemos las condiciones iniciales y la función en el lado derecho de la ecuación (4) con su transformada de Laplace posterior. Para las condiciones iniciales, debe usar la función Racional, ya que el uso del redondeo decimal da como resultado un error.
   
   

    #    : x0 = Rational(6, 5) #   : x01 = Rational(1, 1) g = sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) 

   
   
4. usando (5), reescribimos los derivados convertidos de Laplace incluidos en el lado izquierdo de la ecuación (4), formando el lado izquierdo de esta ecuación a partir de ellos, y comparamos el resultado con su lado derecho:
   
   

    d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg) 

   
   
5. resolvemos la ecuación algebraica obtenida para la transformación X (s) y realizamos la transformación inversa de Laplace:
   
   

    rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t) 

   
   
6. Transferimos del trabajo en la biblioteca SymPy a la biblioteca NumPy:
   
   

    f = lambdify(t, soln, 'numpy') 

   
   
7. trazamos el método Python habitual:
   
   

    x = np.linspace(0, 6*np.pi, 100) plt.title(',     \n  :\n  (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show() 

   
   

Obtenemos:
Versión de la biblioteca Sympy - 1.3



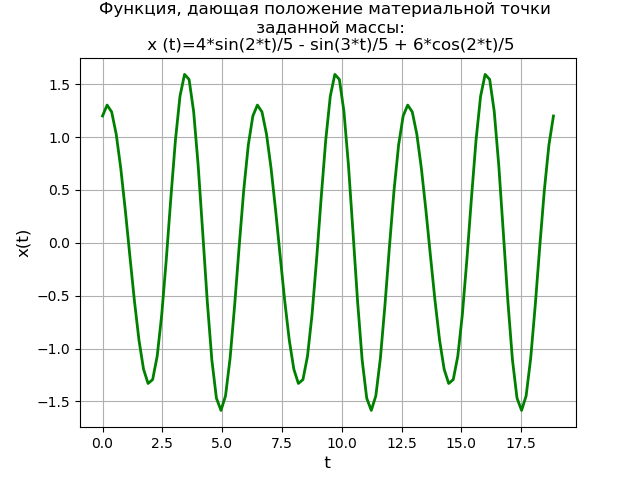
Se obtiene un gráfico de la función periódica que da la posición del punto material de una masa dada. El método de transformación de Laplace que usa la biblioteca SymPy brinda una solución no solo sin la necesidad de encontrar primero una solución general a una ecuación homogénea y una solución particular a la ecuación diferencial heterogénea inicial, sino también sin la necesidad de usar el método de fracción elemental y las tablas de Laplace.

Al mismo tiempo, el valor educativo del método de solución se conserva debido a la necesidad de utilizar el sistema (5) y acudir a NumPy para estudiar soluciones utilizando métodos más productivos.

Para demostrar aún más el método, resolvemos el sistema de ecuaciones diferenciales:
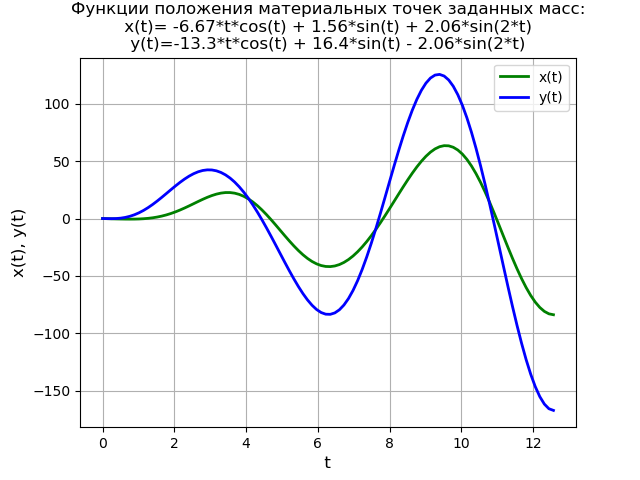
$$$\ begin {cases} 2x '' + 6x-2 = 0, \\ y '' - 2x + 2y = 40 \ cdot \ sin (3t), \ end {cases} (6)$
con condiciones iniciales $$$x (0) = y (0) = y '(0) = 0.$

Un modelo físico simplificado definido por el sistema de ecuaciones (6) bajo cero condiciones iniciales:



Por lo tanto, la fuerza f (t) se aplica repentinamente al segundo punto material de una masa dada en el tiempo t = 0 , cuando el sistema está en reposo en su posición de equilibrio.

La solución del sistema de ecuaciones es idéntica a la solución previamente considerada de la ecuación diferencial (4), por lo tanto, doy el texto del programa sin explicación.


Obtenemos: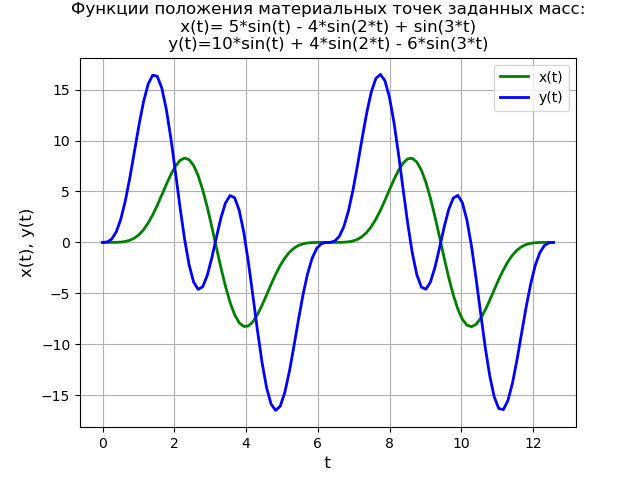



Para condiciones iniciales distintas de cero, el texto del programa y el gráfico de funciones adoptarán la forma:




Considere la solución de una ecuación diferencial lineal de cuarto orden con cero condiciones iniciales:
$$$x ^ {(4)} + 2 \ cdot x '' + x = 4 \ cdot t \ cdot e ^ {t};$
$$$x (0) = x '(0) = x' '(0) = x ^ {(3)} (0) = 0.$


Horario de decisión:



Resolvemos la ecuación diferencial lineal de cuarto orden:
$$$x ^ {(4)} + 13x '' + 36x = 0;$
con condiciones iniciales $$$x (0) = x '' (0) = 0$ , $$$x '(0) = 2$ , $$$x ^ {(3)} (0) = - 13$ .


Horario de decisión: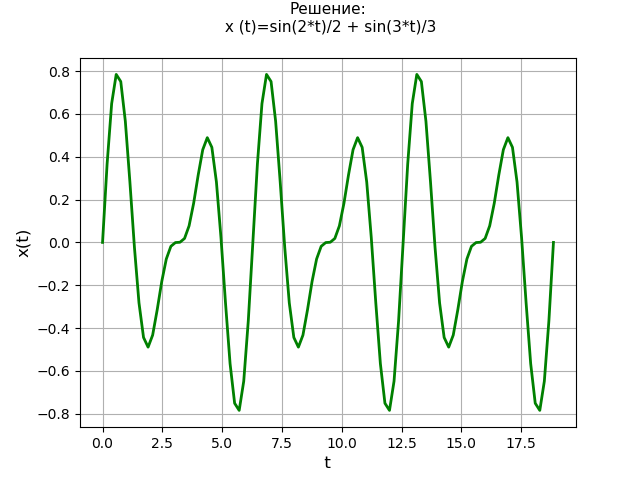

Funciones para resolver ODE

Para los sistemas ODE y ODE con una solución analítica, se utiliza la función dsolve () :
sympy.solvers.ode. dsolve (eq, func = None, pista = 'default', simplify = True, ics = None, xi = None, eta = None, x0 = 0, n = 6, ** kwargs)

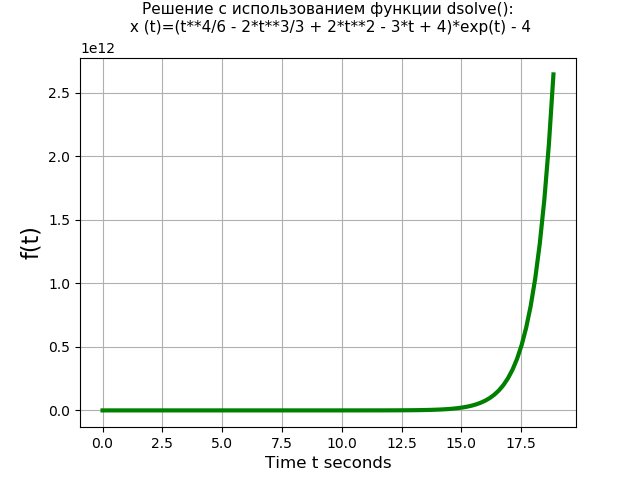
Comparemos el rendimiento de la función dsolve () con el método de Laplace. Por ejemplo, tome la siguiente ecuación diferencial de cuarto grado con cero condiciones iniciales:
$$$x ^ {(IV)} (t) = 3 \ cdot x '' '(t) -x (t) = 4 \ cdot t \ cdot \ exp (t);$
$$$x (0) = x '(0) = x' '(0) = x' '' (0) = 0.$


Obtenemos:

Tiempo de ecuación con la función dsolve (): 1.437 s




Obtenemos:

Tiempo de ecuación usando la transformada de Laplace: 3.274 s



Entonces, la función dsolve () (1.437 s) resuelve la ecuación de cuarto orden más rápido que la solución por el método de transformación de Laplace (3.274 s) más de dos veces. Sin embargo, debe tenerse en cuenta que la función dsolve () no resuelve el sistema de ecuaciones diferenciales de segundo orden, por ejemplo, al resolver el sistema (6) usando la función dsolve (), se produce un error:

 from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez)) 

Obtenemos:

raiseNotImplementedError
NotImplementedError

Este error significa que la solución del sistema de ecuaciones diferenciales que utiliza la función dsolve () no puede representarse simbólicamente. Mientras que con la ayuda de las transformadas de Laplace obtuvimos una representación simbólica de la solución, y esto demuestra la efectividad del método propuesto.

Nota

Para encontrar el método necesario para resolver ecuaciones diferenciales usando la función dsolve () , debe usar classify_ode (eq, f (x)) , por ejemplo:

 from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez) 

Obtenemos:

Eq (f (x), C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('separable', '1st_exact', 'casi_linear', '1st_power_series', 'lie_group', 'separable_Integral', '1st_exact_Integral', 'casi_linear_Integral')
[Eq (f (x), -acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Eq (f (x), acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x)))]]

Por lo tanto, para la ecuación eq = Eq (f (x) .diff (x, x) + f (x), 0) , cualquier método de la primera lista funciona:

nth_linear_constant_coeff_homogeneous,
2nd_power_series_ordinary

Para la ecuación eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) , cualquier método de la segunda lista funciona:

separable, 1st_exact, casi_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, casi_linear_Integral

Para usar el método seleccionado, la entrada de la función dsolve () tomará la forma, por ejemplo:

 rez = dsolve(eq, hint='almost_linear_Integral') 

Conclusión

Este artículo tuvo como objetivo mostrar cómo usar las herramientas de las bibliotecas SciPy y NumPy en el ejemplo de la resolución de sistemas ODE lineales utilizando el método del operador. Así, se consideraron los métodos de solución simbólica de ecuaciones diferenciales lineales y sistemas de ecuaciones por el método de Laplace. Se realiza el análisis del rendimiento de este método y los métodos implementados en la función dsolve ().

Referencias

1. Ecuaciones diferenciales y problemas de valor límite: modelado y cálculo usando Mathematica, Maple y MATLAB. 3ª edición.: Per. del ingles - M .: LLC "I.D. Williams, 2008. - 1104 p .: Ill. - Paral. tit. Ingles
2. Usando la transformación inversa de Laplace para analizar los enlaces dinámicos de los sistemas de control