Aprende OpenGL. Leccion 6.1. PBR o renderizado físicamente correcto. Teoría

Representación físicamente correcta

PBR, o representación basada físicamente, es un conjunto de técnicas de visualización basadas en una teoría que concuerda bastante bien con la teoría real de la propagación de la luz. Dado que el propósito de PBR es una simulación de luz físicamente confiable, parece mucho más realista en comparación con los modelos de iluminación Phong y Blinn-Fong que utilizamos anteriormente. No solo se ve mejor, sino que también brinda una buena aproximación a la física real, lo que nos permite (y a los artistas en particular) crear materiales basados ​​en las propiedades físicas de las superficies sin recurrir a trucos baratos para hacer que la iluminación se vea realista. La principal ventaja de este enfoque es que los materiales que creamos se verán según lo planeado, independientemente de las condiciones de iluminación, lo que no se puede decir sobre otros enfoques, no PBR.

Sin embargo, PBR sigue siendo una aproximación de la realidad (basada en las leyes de la física), por lo que se llama representación físicamente correcta en lugar de representación física. Para que el modelo de iluminación pueda llamarse físicamente correcto, debe cumplir 3 condiciones (no se preocupe, las veremos pronto):

• Basado en un modelo de micro facetas reflectantes.
• Obedecer la ley de conservación de la energía.
• Utilice la función de distribución de reflectancia de doble haz (BRDF)

En esta serie de tutoriales, nos centraremos en el enfoque PBR, desarrollado originalmente en Disney y adaptado para la visualización en tiempo real por Epic Games. Su enfoque, basado en un flujo de trabajo dieléctrico de metal ( flujo de trabajo de Ing. Metallic, no pudo encontrar una mejor traducción, aprox. Ed. ), Está bien documentado, ampliamente aceptado en muchos motores populares y se ve increíble. Al final de esta sección, obtenemos algo similar a esto:

Tenga en cuenta que los artículos de esta sección son bastante avanzados, por lo que se recomienda que comprenda bien OpenGL y la iluminación del sombreador. Estos son algunos de los conocimientos que necesitará para estudiar esta sección: búfer de cuadros , mapas cúbicos , corrección gamma , HDR y mapas normales . También profundizaremos un poco en las matemáticas, pero prometo hacer todo lo posible para explicar todo lo más claramente posible.

Modelo de micro facetas reflectantes

Todas las técnicas de PBR se basan en la teoría de las micro caras. Esta teoría dice que cada superficie a gran aumento puede representarse como un conjunto de espejos microscópicos llamados micro caras . Debido a la rugosidad de la superficie, estos micro-espejos pueden orientarse en diferentes direcciones:

Cuanto más rugosa es la superficie, más al azar se orientan sus microcaras. El resultado de esta disposición de estos pequeños espejos es (en particular cuando se trata de destellos y reflejos especulares) que los rayos de luz incidentes se dispersan en diferentes direcciones en superficies rugosas, lo que conduce a un destello especular más amplio. Y viceversa: en superficies lisas, es más probable que los rayos incidentes se reflejen en una dirección, lo que dará un resplandor más pequeño y más nítido:

A nivel microscópico, no hay superficies absolutamente lisas, pero dado que las microcaras son lo suficientemente pequeñas y no podemos distinguirlas dentro de nuestro espacio de píxeles, aproximamos estadísticamente la rugosidad de la superficie al introducir un coeficiente de rugosidad . Usando este coeficiente, podemos calcular la fracción de microcaras orientadas en la dirección de un determinado vector $$$h$ . Este vector $$$h$ nada más que un vector mediano que yace en el medio entre la dirección de la luz incidente $$$l$ y dirección del observador $$$v$ . Hablamos de eso anteriormente en una lección sobre iluminación avanzada , donde lo definimos como la relación de la suma de vectores $$$l$ y $$$v$ a la longitud del vector resultante:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

Cuantas más micro caras estén orientadas en la dirección del vector mediano, más nítido y brillante será el resaltado especular. Debido al coeficiente de rugosidad, que se encuentra entre 0 y 1, podemos aproximar estadísticamente la orientación de las micro caras:

Como puede ver, un valor más alto del coeficiente de rugosidad proporciona un punto de reflejo de espejo de mayor tamaño, en comparación con un punto pequeño y afilado en superficies lisas.

Conservación de energía.

Usar la aproximación teniendo en cuenta las microcaras ya conlleva una cierta forma de conservación de energía: la energía de la luz reflejada nunca excederá la energía de la luz incidente (si la superficie no brilla por sí misma). Mirando la imagen de arriba, vemos que con un aumento en la rugosidad de la superficie, aumenta el punto de luz reflejada, pero al mismo tiempo disminuye su brillo. Si la intensidad de la luz reflejada fuera la misma para todos los píxeles, independientemente del tamaño del punto, las superficies más rugosas emitirían mucha más energía, lo que violaría la ley de conservación de la energía. Por lo tanto, los reflejos especulares son más brillantes en superficies lisas y tenues en superficies rugosas.

Para que se conserve la energía, debemos hacer una separación clara entre los componentes difusos y espejos. En ese momento, cuando un rayo de luz alcanza la superficie, se divide en componentes reflejados y refractados . El componente reflejado es la luz reflejada directamente y no penetra en la superficie; lo conocemos como un componente espejo de la luz. El componente refractado es la luz que penetra en la superficie y es absorbida por ella; es conocido por nosotros como el componente difuso de la luz.

Pero hay algunos matices asociados con la absorción de luz: no ocurre instantáneamente, tan pronto como la luz toca la superficie. Desde el curso de la física, sabemos que la luz puede describirse como un haz de fotones con energía que se mueve en línea recta hasta que pierde toda la energía como resultado de una colisión con obstáculos. Cada material consta de micropartículas que pueden interactuar con un rayo de luz, como se muestra en la figura a continuación. Estas partículas absorben parte o la totalidad de la energía de la luz en cada colisión, convirtiéndola en calor.

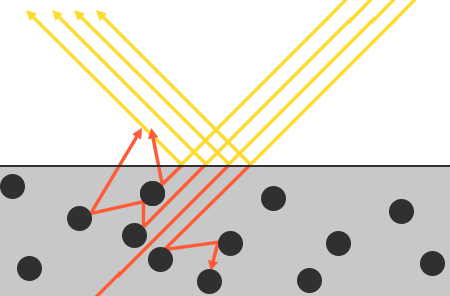
En el caso general, no toda la energía se absorbe, y la luz continúa dispersándose en direcciones (predominantemente) aleatorias, donde nuevamente choca con otras partículas hasta que se queda sin energía o sale de la superficie nuevamente. Por lo tanto, la superficie comienza a reemitir rayos de luz, haciendo una contribución en forma del color observado (difuso) de la superficie. Usando PBR, hacemos la suposición simplificada de que toda la luz refractada es absorbida y dispersada en un área de influencia pequeña, ignorando el efecto de la luz dispersa que abandona la superficie a una distancia de esta área. Las técnicas especiales de sombreado que tienen esto en cuenta, conocidas como técnicas de dispersión subsuperficial , mejoran significativamente la calidad visual de materiales como cuero, mármol, cera, pero son caras en términos de rendimiento.

Aparecen sutilezas adicionales cuando la luz se refracta y se refleja en superficies metálicas . Las superficies metálicas interactúan de manera diferente con la luz que no metálica (es decir, dieléctricos). Obedecen las mismas leyes de refracción y reflexión, con una excepción: toda la luz refractada es absorbida por la superficie sin dispersarse, solo queda la luz reflejada en el espejo; en otras palabras, las superficies metálicas no tienen un color difuso. Debido a esta obvia diferencia entre metales y dieléctricos, se procesarán de manera diferente en el transportador PBR en el que iremos más adelante en el curso de este artículo.

Esta diferencia entre luz reflejada y refractada nos lleva a otra observación con respecto a la conservación de energía: sus valores son mutuamente excluyentes. La energía de la luz reflejada no puede ser absorbida por el material. Por lo tanto, la energía absorbida por la superficie en forma de luz refractada es la energía restante después de tener en cuenta la luz reflejada.
Usamos esta relación, calculando primero la parte reflejada como un porcentaje de la energía de los rayos incidentes reflejados por la superficie, y luego la fracción de la luz refractada directamente del reflejado, como:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

De esta manera, aprendemos los significados de las partes reflejadas y refractadas gracias a la ley de conservación de la energía. Con este enfoque, ni la parte refractada (difusa) ni la reflejada excederán 1.0, asegurando que su energía total no exceda el valor de la energía de luz incidente, que no pudimos tener en cuenta en lecciones anteriores.

Ecuación de reflexión

Lo anterior nos lleva a la llamada ecuación de representación : una ecuación compleja inventada por muchachos muy inteligentes, y hoy es el mejor modelo para simular la iluminación. PBR sigue estrictamente una versión más específica de esta ecuación, conocida como la ecuación de reflexión . Para comprender bien el PBR, es importante tener una comprensión completa de la ecuación de reflexión:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Al principio parece aterrador, pero lo desmontaremos gradualmente, en partes, y verá cuán lentamente comenzará a tener sentido. Para entender esta ecuación tendremos que profundizar un poco más en la radiometría. La radiometría es la ciencia de medir la radiación electromagnética (incluida la luz visible). Hay varias cantidades radiométricas que podemos usar para medir la iluminación, pero solo usaremos una relacionada con la ecuación de reflexión, conocida como Energy Luminance (inglés radiance) y designada aquí por la letra L. EI se usa para cuantificar la magnitud o intensidad de la luz, viniendo de cierta dirección. EJ, a su vez, es una combinación de varias cantidades físicas, y para que nos resulte más fácil imaginarlo, nos centraremos en cada una de ellas individualmente.

Flujo radiante

Flujo de radiación ( $$$\ Phi$ ) es el poder de la energía transmitida por la luz, medida en vatios. La energía total de la luz consta de muchos términos para diferentes longitudes de onda, cada una de las cuales corresponde a su propio color del espectro. La energía emitida por la fuente de luz, en este caso, puede representarse en función de todas estas longitudes de onda. Las longitudes de onda de 390 nm a 700 nm constituyen la parte visible del espectro, es decir, la radiación en este rango puede ser percibida por el ojo humano. En la imagen a continuación puede ver los valores de las energías para diferentes longitudes de onda que componen la luz del día:

El flujo de radiación corresponde al área bajo el gráfico de esta función para todas las longitudes de onda. El uso directo de las longitudes de onda de la luz como entrada en los gráficos de computadora no es práctico, por lo que recurrimos a una representación simplificada del flujo de radiación, en lugar de utilizar una función de todas las longitudes de onda, un triplete de colores, conocido como RGB (o, como generalmente lo llamamos, el color de la iluminación). Tal vista conduce a una pérdida de información, pero en general afectará ligeramente la imagen final.

Ángulo sólido

Ángulo sólido denotado por $$$\ omega$ nos da el tamaño o área de la figura proyectada en la esfera de la unidad. Puedes imaginarlo como una dirección que tiene un volumen de:

Imagina que estás en el centro de una esfera y estás mirando en la dirección de la figura. El tamaño de la silueta resultante será un ángulo sólido.

Intensidad de la radiación

La fuerza de radiación mide la cantidad de flujo de radiación por ángulo sólido, o la fuerza de una fuente de luz por unidad de área definida por el ángulo sólido. Por ejemplo, para una fuente de luz omnidireccional que emite igualmente en todas las direcciones, la fuerza de radiación significa la energía de la luz por área específica (ángulo sólido):

La ecuación que describe la fuerza de la radiación se ve así:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, donde I es el flujo de radiación f por ángulo sólido $$${d \ omega}$

Conociendo el flujo de radiación, la fuerza y ​​el ángulo sólido, podemos describir la ecuación de brillo de energía que describe la energía total observada en el área A, limitada por el ángulo sólido O para la luz por la fuerza $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

El brillo energético es la cantidad radiométrica de luz en un área que depende del ángulo de la luz incidente. $$$\ theta$ (ángulo entre la dirección de la luz y la normal a la superficie) a través $$$cos \ theta$ : La luz es más débil cuando se emite a lo largo de la superficie y es más fuerte cuando está perpendicular a ella. Esto es similar a nuestros cálculos para luz difusa en el tutorial sobre conceptos básicos de iluminación desde $$$cos \ theta$ nada más que un producto escalar entre la dirección de la luz y el vector normal a la superficie:

 float cosTheta = dot(lightDir, N); 

La ecuación de brillo de energía es muy útil para nosotros, porque contiene la mayoría de las cantidades físicas que nos interesan. Si suponemos que el ángulo sólido ω y el área A son infinitesimales, podemos usar el EE para medir el flujo de un rayo de luz por un punto en el espacio. Esto nos permitirá calcular la IE de un solo rayo de luz que actúa sobre un único punto (fragmento); en realidad traducimos el ángulo sólido $$$\ omega$ en vector de dirección $$$\ omega$ y $$$A$ hasta el punto $$$p$ . Por lo tanto, podemos usar directamente la EI en nuestros sombreadores para calcular la contribución de un solo rayo de luz para cada fragmento.

De hecho, cuando se trata de EE, generalmente estamos interesados ​​en todo el incidente de luz entrante en el punto p, que es la suma de todo el EE, y se conoce como irradiancia. Conociendo la IE y la irradiación, podemos volver a la ecuación de reflexión:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Ahora sabemos que $$$L$ en la ecuación de representación es la EI para algún punto de la superficie py un ángulo sólido infinitamente pequeño de la luz entrante $$$\ omega_i$ , que puede considerarse como un vector de dirección de entrada $$$\ omega_i$ . Recuerda que la energía se multiplica por $$$cos \ theta$ - el ángulo entre la dirección de incidencia de la luz y la normal a la superficie, que se expresa en la ecuación de reflexión del producto $$$n \ cdot \ omega_i$ . La ecuación de reflexión calcula la suma de la EI reflejada $$$L_o (p, \ omega_o)$ puntos $$$p$ hacia $$$ω_o$ , que es la dirección saliente para el observador. O si no: $$$L_o$ mide la irradiancia reflejada de un punto $$$p$ si se ve desde $$$\ omega_o$ .

Dado que la ecuación de reflexión se basa en la irradiación, que es la suma de toda la radiación entrante, medimos la luz no solo de una dirección de luz entrante, sino de todas las direcciones de luz entrantes dentro del hemisferio $$$\ Omega$ centrado en $$$p$ . Se puede describir como media esfera orientada a lo largo de la superficie normal $$$n$ :

Para calcular la suma de todos los valores dentro de la región o, en el caso de un hemisferio, el volumen, integramos la ecuación en todas las direcciones entrantes $$$d \ omega_i$ dentro del hemisferio $$$\ Omega$ . Como no existe una solución analítica tanto para la ecuación de render como para la ecuación de reflexión, resolveremos la integral numéricamente. Esto significa que obtendremos resultados para pequeños pasos discretos de la ecuación de reflexión del hemisferio $$$\ Omega$ y promediarlos sobre el tamaño del paso. Esto se llama la suma de Riemann , que podemos representar aproximadamente con el siguiente código:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

dW para cada paso discreto puede considerarse como $$$d \ omega_i$ en la ecuación de reflexión. Matemáticamente $$$d \ omega_i$ es el diferencial por el cual calculamos la integral, y aunque no es lo mismo que dW en el código (ya que este es un paso discreto de la suma de Riemann), podemos considerarlo como tal para facilitar el cálculo. Tenga en cuenta que el uso de pasos discretos siempre nos dará una cantidad aproximada, no el valor exacto de la integral. Un lector atento notará que podemos aumentar la precisión de la suma de Riemann al aumentar el número de pasos.

La ecuación de reflexión resume la radiación de todas las direcciones de luz entrantes. $$$\ omega_i$ hemisferio $$$\ Omega$ eso llega al punto $$$p$ y devuelve la cantidad de luz reflejada $$$L_o$ hacia el espectador. La radiación entrante puede provenir de fuentes de luz con las que ya estamos familiarizados, o de mapas ambientales que determinan el EI de cada dirección entrante, de lo que hablaremos en el tutorial de IBL.

Ahora lo único desconocido a la izquierda es el símbolo $$$f_r$ , conocida como la función BRDF o la función de reflectancia de dos haces , que escala (o pesa) el valor de la radiación entrante en función de las propiedades del material de la superficie.

BRDF

BRDF es una función que acepta la dirección de la luz incidente. $$$\ omega_i$ , dirección al observador $$$\ omega_o$ normal a la superficie $$$n$ y parámetro $$$a$ , que es la rugosidad de la superficie. BRDF se aproxima a la cantidad de cada haz de luz individual $$$\ omega_i$ contribuye a la luz reflejada final de una superficie opaca, teniendo en cuenta las propiedades de su material. Por ejemplo, si la superficie es completamente lisa (casi como un espejo), la función BRDF devolverá 0.0 para todos los rayos de luz entrantes $$$\ omega_i$ excepto uno que tenga el mismo ángulo (después de la reflexión) que el haz $$$\ omega_o$ para lo cual la función devolverá 1.0.

BRDF se aproxima a las propiedades reflectantes y refractivas de un material basado en la teoría de micro caras mencionada anteriormente. Para que el BRDF sea físicamente plausible, debe obedecer la ley de conservación de la energía, es decir, la energía total de la luz reflejada nunca debe exceder la energía de la luz incidente. Técnicamente, el modelo Blinn-Fong se considera un BRDF que acepta lo mismo $$$\ omega_i$ y $$$\ omega_o$ en la entrada Sin embargo, el modelo Blinn-Fong no se considera físicamente correcto, ya que no garantiza el cumplimiento de la ley de conservación de energía. Hay varios BRDF físicamente correctos para aproximar la respuesta de la superficie a la iluminación. Sin embargo, casi todas las canalizaciones de gráficos en tiempo real utilizan el BRDF, conocido como Cook-Torrance BRDF .

Cook-Torrens BRDF contiene una parte difusa y una espejo:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cocinero - torrance}$$

aqui $$$k_d$ - fracción refractada de la energía luminosa entrante, $$$k_s$ - reflejado. El lado izquierdo del BRDF contiene la parte difusa de la ecuación, denotada aquí como $$$f_ {lambert}$ . Esta es la llamada dispersión de Lambert. Es similar a lo que usamos para la iluminación difusa, y es constante:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

donde $$$c$ - albedo o color superficial (textura superficial difusa). División por $$$\ pi$ necesario para normalizar la luz dispersa, ya que la integral que contiene BRDF anteriormente indicada se multiplica por $$$\ pi$ (llegaremos a esto en el tutorial de IBL).

Puede que se sorprenda de cómo esta dispersión lambertiana se asemeja a la expresión de iluminación difusa que usamos antes: el color de la superficie multiplicado por el producto escalar entre la superficie normal y la dirección de la luz. El producto escalar todavía está presente, pero se infiere del BRDF, ya que tenemos $$$n \ cdot \ omega_i$ en la integral $$$L_o$ .

Hay varias ecuaciones para la parte difusa de BRDF que parecen más realistas, pero son más caras en términos de rendimiento. Además, como concluyeron los Epic Games: la dispersión lambertiana es suficiente para la mayoría de los propósitos de renderizado en tiempo real.

La porción del espejo del Cook-Torrens BRDF se mejora ligeramente y se describe como:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

Consta de tres funciones y un coeficiente de estandarización en el denominador. Cada una de las letras D, F y G representa un cierto tipo de función que se aproxima a una cierta parte de las propiedades reflectantes de la superficie. Se conocen como la función de distribución normal (NDF), la ecuación de Fresnel y la función de geometría:

• Función de distribución normal: aproxima el número de microfaces de superficie orientadas a lo largo del vector mediano, en función de la rugosidad de la superficie; Esta es la función principal que se aproxima a las micro caras.
• Función de geometría: describe la propiedad de sombreado automático de las micro caras. Cuando la superficie es bastante rugosa, algunas microcaras de la superficie pueden superponerse a otras, reduciendo así la cantidad de luz reflejada por la superficie.
• Ecuación de Fresnel: describe el coeficiente de reflexión de la superficie en diferentes ángulos.

Cada una de estas funciones es una aproximación de su equivalente físico, y para ellas hay varias implementaciones destinadas a una aproximación más precisa al modelo físico subyacente; algunos dan resultados más realistas, otros son más efectivos en términos de rendimiento. Brian Caris, de Epic Games, ha investigado mucho sobre diferentes tipos de aproximaciones, sobre las que puede obtener más información aquí . Utilizaremos las mismas funciones que en Unreal Engine 4 de Epic Games, a saber: Trowbridge-Reitz GGX para D, aproximación de Fresnel-Schlick para F y Smith's Schlick-GGX para G.

Función de distribución normal

La función de distribución normal D aproxima estadísticamente el área de superficie relativa de las micro caras que están orientadas con precisión a lo largo del vector mediano $$$h$ . Hay muchos NDF que determinan la aproximación estadística de la alineación general de las micro caras teniendo en cuenta algunos parámetros de rugosidad. Utilizaremos uno conocido como Trowbridge-Reitz GGX:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

aqui $$$h$ Es el vector mediano $$$\ alpha$ - valor de la rugosidad de la superficie. Si elegimos $$$h$ como el vector mediano entre lo normal a la superficie y la dirección de la luz, luego cambiando el parámetro de rugosidad, obtenemos la siguiente imagen:

Cuando la rugosidad es pequeña (es decir, la superficie es lisa), las micro caras orientadas en la dirección del vector mediano se concentran en un radio pequeño. Debido a esta alta concentración, NDF da un punto muy brillante. En una superficie rugosa, donde las micro caras están orientadas en direcciones más aleatorias, encontrará un número mucho mayor de micro caras orientadas en la dirección del vector mediano $$$h$ pero ubicado en un radio mayor, lo que hace que el color plano sea más gris.

En el código GLSL, la función de distribución normal Trowbridge-Reitz GGX se verá así:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

Función de geometría

La función de geometría se aproxima estadísticamente al área de superficie relativa, donde se superponen sus irregularidades microscópicas, lo que evita que penetren los rayos de luz.

Como en el caso de NDF, la función de geometría acepta el coeficiente de rugosidad de la superficie como entrada, lo que en este caso significa lo siguiente: las superficies más rugosas tendrán una mayor probabilidad de sombrear las microcaras. La función de geometría que utilizaremos es una combinación de las aproximaciones de GGX y Schlick-Beckmann, y se conoce como Schlick-GGX:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

Aqui $$$k$ es una redesignación $$$\ alpha$ dependiendo de si usamos la función de geometría para iluminación directa o iluminación IBL:

$$

$$k_ {directo} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

Tenga en cuenta que el valor $$$\ alpha$ puede variar dependiendo de cómo su motor traduzca la aspereza en $$$\ alpha$ . En las siguientes lecciones discutiremos en detalle cómo y dónde esta reasignación se vuelve relevante.

Para aproximar efectivamente la geometría, debemos tener en cuenta tanto la dirección de la vista (geometría superpuesta) como el vector de dirección de la luz (auto-sombreado de la geometría). Podemos considerar ambos casos utilizando el método Smith :

$$

$$G (n, v, l, k) = G_ {sub} (n, v, k) G_ {sub} (n, l, k)$$

Usando el Método Smith con Schlick-GGX como $$$G_ {sub}$ da la siguiente imagen con diferente rugosidad R:

La función de geometría es un factor entre [0.0, 1.0], donde el blanco (o 1.0) significa que no hay sombreado de las micro-caras, y el negro (o 0.0) significa el sombreado completo de las micro-caras.

En GLSL, una función de geometría se convierte al siguiente código:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

Ecuación de Fresnel

La ecuación de Fresnel describe la proporción de luz reflejada y refractada, que depende del ángulo en el que miramos la superficie. Cuando la luz golpea una superficie, la ecuación de Fresnel nos da el porcentaje de luz reflejada en función del ángulo en el que vemos esta superficie. A partir de esta relación de reflexión y la ley de conservación de la energía, podemos obtener directamente la parte refractada de la luz, que será igual a la energía restante.

Cada superficie o material tiene un nivel de reflectividad básica , que se observa cuando se mira directamente a la superficie, pero si se observa la superficie en ángulo, todas las reflexiones se vuelven más notables. Puede verificar esto usted mismo mirando su mesa probablemente de madera o metal primero perpendicularmente y luego en un ángulo cercano a 90 grados. Verá que los reflejos se vuelven mucho más notables. Todas las superficies, teóricamente, reflejan completamente la luz cuando se ven desde ellas en un ángulo ideal de 90 grados. Este efecto se llama Fresnel y se describe mediante la ecuación de Fresnel .

La ecuación de Fresnel es bastante compleja, pero, afortunadamente, se puede simplificar usando la aproximación de Fresnel-Schlick :

$$

$$F_ {Schlick} (h, v, F_0) = F_0 + (1 - F_0) (1− (h \ cdot v)) ^ 5$$

$$$F_0$ representa la reflectividad básica de la superficie, que calculamos utilizando algo llamado índices de refracción o IOR (índices de refracción) y, como puede ver en la superficie de la esfera, cuanto más cerca esté la dirección de visualización de los límites de la esfera visible (el ángulo entre la dirección de visualización y la mediana) 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

Materiales relacionados

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.