El principio de menor acción. Parte 2

La última vez examinamos brevemente uno de los principios físicos más notables: el principio de menor acción, y nos decidimos por un ejemplo que, al parecer, lo contradice. En este artículo, trataremos este principio con más detalle y veremos qué sucede en este ejemplo.

Esta vez necesitamos un poco más de matemáticas. Sin embargo, intentaré exponer la parte principal del artículo nuevamente a nivel elemental. Destacaré puntos un poco más rigurosos y complejos, se pueden omitir sin perjuicio de la comprensión básica del artículo.

Condiciones de contorno

Comenzaremos con el objeto más simple: una bola que se mueve libremente en el espacio, sobre la cual no actúan fuerzas. Tal bola, como se sabe, se mueve de manera uniforme y rectilínea. Para simplificar, suponga que se mueve a lo largo del eje $$$x$ :

Para describir con precisión su movimiento, como regla, se especifican las condiciones iniciales. Por ejemplo, se especifica que en el momento inicial del tiempo $$$t_A$ la pelota estaba en un punto $$$A$ con coordenadas $$$x_A$ y tenía velocidad $$$v_A$ . Después de establecer las condiciones iniciales de esta forma, determinamos de manera única el movimiento adicional de la pelota: se moverá a una velocidad constante y su posición en el momento $$$t$ será igual a la posición inicial más la velocidad multiplicada por el tiempo transcurrido: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ . Esta forma de establecer las condiciones iniciales es muy natural e intuitivamente familiar. Pedimos toda la información necesaria sobre el movimiento de la pelota en el momento inicial, y luego su movimiento está determinado por las leyes de Newton.

Sin embargo, esta no es la única forma de especificar el movimiento de la pelota. Otra forma alternativa es establecer la posición de la pelota en dos puntos diferentes en el tiempo. $$$t_A$ y $$$t_B$ . Es decir pregunta eso:

1) a tiempo $$$t_A$ la pelota estaba en un punto $$$A$ (con coordenada $$$x_A$ );
2) a tiempo $$$t_B$ la pelota estaba en un punto $$$B$ (con coordenada $$$x_B$ )

La expresión "estaba en un punto $$$A$ "No significa que la pelota haya descansado en un punto $$$A$ . A tiempo $$$t_A$ él podría volar sobre un punto $$$A$ . Significa que su posición en el tiempo $$$t_A$ coincidió con un punto $$$A$ . Lo mismo se aplica al punto $$$B$ .

Estas dos condiciones también determinan de manera única el movimiento de la pelota. Su movimiento es fácil de calcular. Para satisfacer ambas condiciones, la velocidad de la pelota obviamente debe ser $$$(x_B-x_A) / (t_B-t_A)$ . Posición de la pelota en el momento $$$t$ nuevamente será igual a la posición inicial más la velocidad multiplicada por el tiempo transcurrido:

$$

$$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

Tenga en cuenta que en las condiciones del problema no necesitábamos establecer la velocidad inicial. Se determina únicamente a partir de las condiciones 1) y 2).

Establecer condiciones en la segunda forma parece inusual. Quizás no esté claro por qué en general puede ser necesario preguntarles de esta forma. Sin embargo, en el principio de menor acción, se utilizan precisamente las condiciones en la forma 1) y 2), y no en la forma de establecer la posición inicial y la velocidad inicial.

Trayectoria de menor acción

Ahora pasemos un poco del movimiento libre real de la pelota y consideremos el siguiente problema puramente matemático. Supongamos que tenemos una bola que podemos mover manualmente de la forma que queramos. En este caso, debemos cumplir las condiciones 1) y 2). Es decir en el medio $$$t_A$ y $$$t_B$ tenemos que moverlo desde el punto $$$A$ hasta el punto $$$B$ . Esto se puede hacer de maneras completamente diferentes. Cada uno de estos métodos se llamará la trayectoria de la pelota y se puede describir por la función de la posición de la pelota a tiempo $$$x (t)$ . Pospongamos varias de esas trayectorias en el gráfico de la dependencia de la posición de la pelota en el tiempo:

Por ejemplo, podemos mover la pelota a la misma velocidad igual a $$$(x_B-x_A) / (t_B-t_A)$ (camino verde). O podemos mantenerlo a medio punto $$$A$ y luego doble velocidad para moverse al punto $$$B$ (trayectoria azul). Primero puede moverlo en la dirección opuesta. $$$B$ lado y luego ya se mueven a $$$B$ (trayectoria marrón). Puedes moverlo de un lado a otro (trayectoria roja). En general, puede moverlo como desee, si solo se observan las condiciones 1) y 2).

Para cada trayectoria, podemos unir un número. En nuestro ejemplo, es decir en ausencia de fuerzas que actúen sobre la pelota, este número es igual a la energía cinética acumulada total durante todo el tiempo de su movimiento en el intervalo entre $$$t_A$ y $$$t_B$ y se llama una acción.

En este caso, la palabra energía cinética "acumulada" no transmite con precisión el significado. En realidad, la energía cinética no se acumula en ninguna parte; la acumulación se usa solo para calcular la acción de la trayectoria. En matemáticas, para tal acumulación hay un muy buen concepto: la integral:

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} Tdt$$

La acción generalmente se indica con la letra $$$S$ . Símbolo $$$T$ significa energía cinética. Esta integral significa que la acción es igual a la energía cinética acumulada de la pelota durante un período de tiempo desde $$$t_A$ antes $$$t_B$ .

Como ejemplo, tomemos una pelota que pese 1 kg., Establezca algunas condiciones de contorno y calcule la acción para dos trayectorias diferentes. Deja el punto $$$B$ está a 1 metro del punto $$$A$ y tiempo $$$t_B$ distante del tiempo $$$t_A$ por 1 segundo Es decir debemos mover la pelota que en el momento inicial estaba en el punto $$$A$ , en un segundo a una distancia de 1 m a lo largo del eje $$$x$ .

En el primer ejemplo (trayectoria verde) movimos la pelota de manera uniforme, es decir con la misma velocidad, que, obviamente, debería ser igual a: $$$v = 1$ m / s La energía cinética de la pelota en cada momento es igual a: $$$T = mv ^ 2/2$ = 1/2 J. En un segundo, 1/2 J se acumulará $$$\ cdot$ con energía cinética Es decir válido para tal trayectoria es: $$$S = 1/2$ J $$$\ cdot$ s

Ahora no transfiramos inmediatamente la pelota desde el punto $$$A$ hasta el punto $$$A$ y manténgalo en un punto durante medio segundo $$$A$ , y luego, durante el tiempo restante, lo transferimos uniformemente al punto $$$B$ . En el primer medio segundo, la pelota está en reposo y su energía cinética es cero. Por lo tanto, la contribución a la acción de esta parte de la trayectoria también es igual a cero. Para el segundo medio segundo transferimos la pelota a doble velocidad: $$$v = 2$ m / s La energía cinética será igual a $$$T = mv ^ 2/2$ = 2 J. La contribución de este período de tiempo a la acción será 2 J multiplicada por medio segundo, es decir. 1 J $$$\ cdot$ s Por lo tanto, la acción general para tal trayectoria es igual a $$$S = 1$ J $$$\ cdot$ s

De manera similar, cualquier otra trayectoria con las condiciones de contorno especificadas 1) y 2) corresponde a un cierto número igual a la acción para una trayectoria dada. Entre todas estas trayectorias, hay una trayectoria en la que la acción es la menor. Se puede demostrar que esta trayectoria es una trayectoria verde, es decir movimiento uniforme de la pelota. Para cualquier otra trayectoria, no importa cuán difícil sea, la acción será más de 1/2.

En matemáticas, dicha comparación para cada función de un número determinado se llama funcional. Muy a menudo en física y matemáticas, surgen tareas como la nuestra, es decir para encontrar una función para la cual el valor de un funcional particular es mínimo. Por ejemplo, una de las tareas de gran importancia histórica para el desarrollo de las matemáticas es el problema de la bachistochrone . Es decir Encontrar una curva a lo largo de la cual la bola rueda más rápido. Nuevamente, cada curva puede ser representada por la función h (x), y a cada función se le puede asignar un número, en este caso el tiempo de rodadura de la pelota. Una vez más, el problema se reduce a encontrar una función para la cual el valor de lo funcional sea mínimo. El área de las matemáticas que se ocupa de tales problemas se llama cálculo de variaciones.

Principio de menor acción

En los ejemplos discutidos anteriormente, tenemos dos trayectorias especiales obtenidas de dos maneras diferentes.

La primera trayectoria se obtiene de las leyes de la física y corresponde a la trayectoria real de una bola libre, que no se ve afectada por ninguna fuerza y ​​cuyas condiciones límite se dan en las formas 1) y 2).

La segunda trayectoria se obtiene del problema matemático de encontrar una trayectoria con las condiciones límite 1) y 2), para las cuales la acción es mínima.

El principio de menor acción establece que estas dos trayectorias deben coincidir. En otras palabras, si se sabe que la bola se movió de tal manera que se cumplieron las condiciones límite 1) y 2), entonces necesariamente se movió a lo largo de una ruta para la cual la acción es mínima en comparación con cualquier otra ruta con las mismas condiciones límite.

Uno podría considerar esto como una mera coincidencia. Hay muchos problemas en los que aparecen trayectorias uniformes y líneas rectas. Sin embargo, el principio de menor acción es un principio muy general, válido en otras situaciones, por ejemplo, para el movimiento de la pelota en un campo gravitacional uniforme. Para hacer esto, solo necesita reemplazar la energía cinética con la diferencia en energía cinética y potencial. Esta diferencia se llama la función Lagrangiana o Lagrange y la acción ahora se vuelve igual al total de Lagrangian acumulado. De hecho, la función Lagrange contiene toda la información necesaria sobre las propiedades dinámicas del sistema.

Si lanzamos una pelota en un campo de gravedad uniforme para que pase un punto $$$A$ a tiempo $$$t_A$ y voló al punto $$$B$ a tiempo $$$t_B$ , entonces él, de acuerdo con las leyes de Newton, volará una parábola. Es esta parábola que coincide con las trayectorias para las cuales la acción será mínima.

Por lo tanto, para un cuerpo que se mueve en un campo potencial, por ejemplo, en el campo gravitacional de la Tierra, la función de Lagrange es igual a: $$$L = T (v) -V (x, y, z)$ . Energía cinética $$$T$ depende de la velocidad del cuerpo y del potencial, de su posición, es decir coordenadas $$$x, y, z$ . En mecánica analítica, el conjunto completo de coordenadas que determinan la posición de un sistema generalmente se denota con una letra $$$q$ . Para una pelota que se mueve libremente en un campo gravitacional, $$$q$ significa coordenadas $$$x$ , $$$y$ y $$$z$ .

Para indicar la tasa de cambio de una cantidad, en física muy a menudo simplemente ponen fin a esta cantidad. Por ejemplo $$$\ dot x$ indica la tasa de cambio de coordenada $$$x$ o, en otras palabras, la velocidad del cuerpo en la dirección $$$x$ . Usando estas convenciones, la velocidad de nuestra pelota en mecánica analítica se denota como $$$\ dot q$ . Es decir $$$\ dot q$ componentes de velocidad media $$$v_x, v_y, v_z$ .

Dado que la función Lagrange depende de la velocidad y las coordenadas, también puede depender explícitamente del tiempo (explícitamente depende del tiempo significa que el valor $$$L$ en diferentes momentos, diferentes, a las mismas velocidades y posiciones de la pelota), entonces la acción en forma general se escribe como

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} L (\ dot q, q, t) dt$$

No siempre mínimo

Sin embargo, al final de la parte anterior, vimos un ejemplo en el que el principio de menor acción claramente no funciona. Para hacer esto, nuevamente tomamos una bola libre, que no se ve afectada por ninguna fuerza, y colocamos una pared de resorte al lado.
Establecemos las condiciones de contorno de manera que los puntos $$$A$ y $$$B$ emparejar Es decir y a la vez $$$t_A$ y a la vez $$$t_B$ la pelota debe estar en el mismo punto $$$A$ . Una de las posibles trayectorias será la posición de la pelota en su lugar. Es decir todo el tiempo entre $$$t_A$ y $$$t_B$ él se parará en un punto $$$A$ . La energía cinética y potencial en este caso será igual a cero, por lo tanto, la acción para tal trayectoria también será igual a cero.

Estrictamente hablando, la energía potencial puede tomarse no igual a cero, sino a cualquier número, ya que la diferencia en la energía potencial en diferentes puntos del espacio es importante. Sin embargo, un cambio en el valor de la energía potencial no afecta la búsqueda de una trayectoria con una acción mínima. Es solo que para todas las trayectorias, el valor de la acción cambiará en el mismo número, y la trayectoria con acción mínima seguirá siendo la trayectoria con acción mínima. Por conveniencia, para nuestra pelota elegiremos la energía potencial igual a cero.

Otra posible trayectoria física con las mismas condiciones de contorno sería una trayectoria en la cual la pelota vuela primero a la derecha, pasando un punto $$$A$ a tiempo $$$t_A$ . Luego choca con el resorte, lo comprime, el resorte se endereza, empuja la pelota hacia atrás y nuevamente vuela más allá del punto $$$A$ . Puedes elegir la velocidad de la pelota para que, rebotando en la pared, vuele un punto $$$A$ justo en este momento $$$t_B$ . La acción con esta trayectoria será básicamente igual a la energía cinética acumulada durante el vuelo entre el punto. $$$A$ y pared y espalda. Habrá un cierto período de tiempo cuando la bola comprima el resorte y aumente su energía potencial, y durante este período la energía potencial hará una contribución negativa a la acción. Pero ese período de tiempo no será muy largo y la acción no se reducirá en gran medida.



La figura muestra las dos trayectorias físicamente posibles de la pelota. El camino verde corresponde a una pelota en reposo, mientras que el azul corresponde a una pelota que rebota en la pared del resorte.

Sin embargo, solo uno de ellos tiene un efecto mínimo, ¡el primero! La segunda trayectoria tiene más acción. Resulta que en este problema hay dos trayectorias físicamente posibles y solo una con una acción mínima. Es decir en este caso, el principio de menor acción no funciona.

Puntos estacionarios

Para entender cuál es el problema aquí, vamos a desviarnos del principio de menor acción por el momento y tomemos las funciones habituales. Tomemos alguna función $$$y (x)$ y dibuja su horario:

En el gráfico, marqué cuatro puntos especiales en verde. ¿Qué es común a estos puntos? Imagine que un gráfico de función es una diapositiva real sobre la que puede rodar una bola. Los cuatro puntos marcados son especiales porque si instala la bola exactamente en este punto, no rodará en ningún lado. En todos los demás puntos, por ejemplo, el punto E, no podrá permanecer en su lugar y comenzará a deslizarse hacia abajo. Dichos puntos se llaman estacionarios. Encontrar estos puntos es una tarea útil, ya que cualquier máximo o mínimo de la función, si no tiene torceduras agudas, debe ser un punto estacionario.

Si clasificamos con mayor precisión estos puntos, entonces el punto A es el mínimo absoluto de la función, es decir, su valor es menor que cualquier otro valor de función. Punto B: no es un máximo ni un mínimo, y se denomina punto de silla de montar. El punto C se llama máximo local, es decir el valor en ella es mayor que en los puntos vecinos de la función. Y el punto D es un mínimo local, es decir el valor en ella es menor que en los puntos vecinos de la función.

La búsqueda de tales puntos se lleva a cabo mediante una rama de las matemáticas llamada análisis matemático. De otra manera, a veces se le llama análisis de infinitesimal, ya que sabe cómo trabajar con cantidades infinitesimales. Desde el punto de vista del análisis matemático, los puntos estacionarios tienen una propiedad especial, gracias a la cual se encuentran. Para comprender qué es esta propiedad, debemos comprender cómo se ve la función a distancias muy pequeñas desde estos puntos. Para hacer esto, tomamos un microscopio y lo miramos en nuestros puntos. La figura muestra cómo se ve la función cerca de varios puntos con diferentes aumentos.

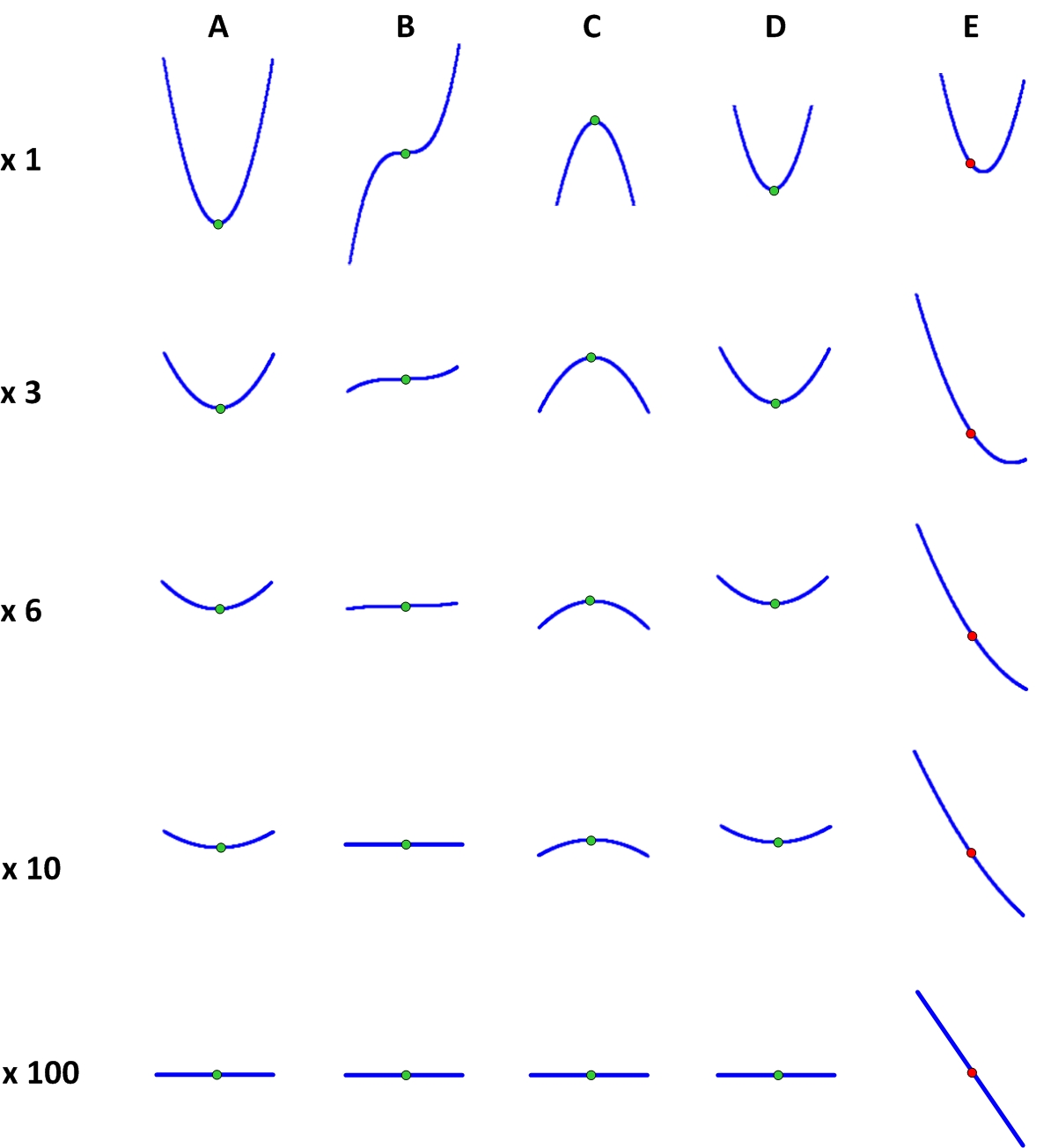
Se puede ver que con un aumento muy grande (es decir, con desviaciones muy pequeñas x), los puntos estacionarios se ven exactamente iguales y difieren mucho del punto no estacionario. Es fácil entender cuál es esta diferencia: la gráfica de la función en un punto estacionario con el aumento se convierte en una línea estrictamente horizontal, y en una no estacionaria se convierte en una línea inclinada. Es por eso que una bola montada en un punto estacionario no rodará.

La horizontalidad de la función en el punto estacionario se puede expresar de manera diferente: la función en el punto estacionario prácticamente no cambia con un cambio muy pequeño en su argumento $$$x$ , incluso en comparación con el argumento en sí. La función está en un punto no estacionario con un pequeño cambio. $$$x$ varía en proporción a $$$x$ . Y cuanto mayor es el ángulo de la función, más fuerte cambia la función al cambiar $$$x$ . De hecho, la función con tamaño creciente se vuelve cada vez más similar a la tangente a la gráfica en el punto en cuestión.

En lenguaje matemático estricto, la expresión "función prácticamente no cambia en un punto $$$x_0$ con muy poco cambio $$$x$ "Significa que la relación entre el cambio de función y el cambio de su argumento $$$Δy / Δx$ tiende a 0 en $$$∆x$ tendiendo a 0:

$$$$ display $$ \ lim_ {Δx \ to 0} \ frac {Δy (x_0)} {Δx} = \ lim_ {x \ to 0} \ frac {y (x_0 + Δx) -y (x_0) } {∆x} = 0 $$ mostrar $$

Para un punto no estacionario, esta relación tiende a un número distinto de cero, que es igual a la pendiente de la función en este punto. El mismo número se llama la derivada de la función en un punto dado. La derivada de la función muestra qué tan rápido cambia la función cerca de un punto dado con un pequeño cambio en su argumento $$$x$ . Por lo tanto, los puntos estacionarios son puntos en los que la derivada de la función es 0.

Trayectorias estacionarias

Por analogía con los puntos estacionarios, se puede introducir el concepto de trayectorias estacionarias. Recuerde que cada trayectoria corresponde a un cierto valor de acción, es decir algún número Entonces puede haber una trayectoria tal que para las trayectorias cercanas con las mismas condiciones de contorno, los valores de acción correspondientes prácticamente no diferirán de la acción para la trayectoria estacionaria misma. Tal trayectoria se llama estacionaria. En otras palabras, cualquier trayectoria cercana a la estacionaria tendrá un valor de acción que difiere muy poco de la acción para esta trayectoria estacionaria.

Nuevamente, en el lenguaje matemático "poco diferente" tiene el siguiente significado exacto. Digamos que tenemos un funcional $$$S (x (t))$ para funciones con las condiciones límite requeridas 1) y 2), es decir $$$x (t_A) = A$ y $$$x (t_B) = B$ . Supongamos que la trayectoria $$$x (t)$ - estacionario

Podemos tomar cualquier otra función $$$g (t)$ tal que al final toma valores cero, es decir $$$g (t_A)$ = $$$g (t_B)$ = 0. También tome la variable $$$ε$ que haremos cada vez menos. De estas dos funciones y variables $$$ε$ podemos hacer una tercera función $$$x '(t) = x (t) + εg (t)$ , $$$f'(t_A)=A$ y $$$f'(t_B)=B$ . $$$ε$ , $$$x'(t)$ , $$$x(t)$ .

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ . Es decir

$$

$$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ . «» « ».

$$$δS=0$ .

Dos matemáticos encontraron Euler y Lagrange el método para encontrar funciones estacionarias (no solo por el principio de menor acción, sino también por muchos otros problemas). Resulta que la función estacionaria, cuya función funcional se expresa mediante una integral similar a la integral de acción, debe satisfacer una cierta ecuación, que ahora se llama ecuación de Euler-Lagrange.

Principio estacionario

La situación con un mínimo de acción para trayectorias es similar a la situación con un mínimo de funciones. Para que la trayectoria tenga el menor efecto, debe ser una trayectoria estacionaria. Sin embargo, no todas las trayectorias estacionarias son trayectorias con acción mínima. Por ejemplo, una trayectoria estacionaria puede tener una acción mínima localmente. Es decirsu acción será menor que la de cualquier otra trayectoria adyacente. Sin embargo, en algún lugar lejano puede haber otras trayectorias para las cuales la acción será aún menor.

Resulta que los cuerpos reales no necesariamente se mueven a lo largo de trayectorias con la menor acción. Pueden moverse a lo largo de un conjunto más amplio de trayectorias especiales, a saber, trayectorias estacionarias. Es decirLa trayectoria real del cuerpo siempre será estacionaria. Por lo tanto, el principio de menor acción se llama más correctamente el principio de acción estacionaria. Sin embargo, según la tradición establecida, a menudo se le llama el principio de menor acción, lo que implica para esto no solo la minimidad, sino también la estacionariedad de las trayectorias.

Ahora podemos escribir el principio de la acción estacionaria en un lenguaje matemático, como generalmente se escribe en los libros de texto:

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

.

Aqui $$$q$Son coordenadas generalizadas, es decir Un conjunto de variables que especifican de forma exclusiva la posición del sistema.
$$$\dot q$ - la tasa de cambio de coordenadas generalizadas.
$$$L(\dot q,q,t)$ - la función de Lagrange, que depende de las coordenadas generalizadas, sus velocidades y, posiblemente, el tiempo.
$$$S$ - una acción que depende de la trayectoria específica del sistema (es decir, $$$q(t)$ )

Las trayectorias reales del sistema son estacionarias, es decir. para ellos una variación de acción$$$δS=0$ .

Si volvemos al ejemplo con una pelota y una pared elástica, la explicación de esta situación ahora se vuelve muy simple. Dadas las condiciones de contorno que la pelota también debe$$$t_A$ y durante $$$t_B$ llegar al punto $$$A$ . . , . , , . .

( ) , .