
Lo más probable es que tenga una pregunta razonable: ¿por qué?
Desde un punto de vista pragmático, no hay necesidad) Siempre puede usar Tungsteno condicional, y si necesita hacer esto en python, use módulos especiales que no son tan difíciles de dominar.
Pero si de repente se le dio esa tarea o si realmente le gusta la programación, como a mí, entonces tendrá emocionantes, y a veces no muy, horas de escribir un programa y depurarlo)
Al escribir esta obra maestra, realmente necesitamos una depuración paso a paso, así que descargue PyCharm, VS o algo más con esta función. Para construir tablas, la falta de esta función no es tan crítica, pero para trazar ...
Entonces, ¿cuál será mi programa? En la entrada, tomará tres valores: el comienzo y el final del segmento en el que queremos ver nuestra función y el paso con el que nos moveremos. A continuación, dibujaremos una tabla de valores de función en cada punto del rango de valores especificado por los datos de entrada. Bueno, entonces dibujaremos la gráfica de la función en sí con el eje y en movimiento.
Así que vamosPara comenzar, declararé varias funciones cuyos valores consideraremos. Tomaré especialmente bastante simple
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
Ahora tenemos tres funciones, dos de las cuales tienen un punto de ruptura. Desde el módulo matemático, que almacena todos los bollos matemáticos (incluidos cosenos, arcotangentes y otros trigonometría), importamos sqrt, es decir, la raíz cuadrada. Lo necesitamos para leer la función y3.
Después de eso, necesitamos leer el rango de la función por x y el paso con el que pasamos por este rango. Para esto, usaré el mapa.
Como primer parámetro, esta función toma alguna función que de alguna manera transforma los datos que necesitamos, y como segundo argumento, algún tipo de hoja de datos que necesitamos procesar
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
Leemos los tres valores ingresados a través de un espacio, los dividimos en elementos por un espacio (usando el método de división, que, cuando se llama sin parámetros, dividirá automáticamente la cadena que especifique por espacios). Los datos ingresados usando input () serán por defecto de tipo str, es decir, una cadena, por lo que no tendremos ningún error aquí.
Dado que los números de límite de rango pueden ser fraccionarios, convertimos cada elemento de la matriz resultante en un número real utilizando la función flotante.
Tenga en cuenta que las variables se declaran sin especificar un tipo de datos. Se determina automáticamente (el tipo de datos del valor que está intentando asignar a una variable), o usando las funciones str, int, float, etc. establecido manualmente por variables, aplicando estas mismas funciones a los valores. La misma variable puede tener un tipo de datos diferente en todo el programa: simplemente asigne un nuevo valor con un tipo de datos diferente.
Por ejemplo
auxiliary_variable = ""
Volvamos a nuestro programa. Necesitamos verificar si los datos ingresados son correctos.
El programa debe imprimir que los datos ingresados son incorrectos si:
- el paso es 0
- el límite inferior del rango es mayor que el superior, y el paso es positivo (es decir, tenemos una progresión aritmética de la forma xn = from_x + pace_x * (n - 1) , en la cual from_x> to_x . Dado que pace_x> 0, esta progresión aumentará y nosotros nunca llegue a_x )
- el límite inferior del rango es menor que el superior, y el paso es negativo (razonamiento similar)
- los gráficos que consisten en un punto no son informativos, por lo tanto, el segmento en el que construimos la función debe contener al menos dos valores
Formulamos estas condiciones en el código. Obviamente, el primer elemento es fácil de configurar. El segundo y el tercero se pueden combinar en uno, si observa que el signo de la diferencia entre el primero (from_x) y el último (to_x) debe coincidir con el signo del paso. Bueno, el cuarto punto tampoco es tan complicado: el módulo de la diferencia del primer y último valor no debe ser menor que el módulo de pasos.
Debido al módulo, podemos tener una situación en la que los signos de la diferencia y el paso no coincidirán, pero la segunda condición cortará estos casos, por lo que la condición es correcta.
Como resultado, estas tres condiciones se verán así:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
Procedemos directamente a la mesa. Para facilitar la depuración, crearé varias variables con nombres para hablar que serán responsables de la precisión de los números, el número de espacios antes del número, el número de espacios después del número, etc.
dials_precision = "%10.6g"
Entonces, ¿qué está pasando aquí?

dials_precision = "%10.6g"
en esta línea establezco la precisión del número. Máximo 10 caracteres para el número entero y 6 caracteres para la parte fraccionaria. Si tenemos un valor demasiado grande para este rango, aparecerán todo tipo de
e-15 o algo similar.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision es una cadena, por lo que podemos tomar una porción de esta cadena, es decir, algún tipo de subcadena. En este caso, necesitamos obtener el número 10, por lo que tomamos los caracteres en los índices 1 y 2, convertimos esta subcadena en un tipo de datos entero, lo dividimos por dos y lo redondeamos hacia abajo.
Necesitamos esta variable para que las inscripciones en el encabezado de la tabla estén centradas en la celda.
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
Como su nombre lo indica, esta variable es responsable de la longitud de los límites inferiores de las celdas de la tabla de valores de la función. En total, el número ocupa 10 posiciones, lo que significa que la columna no puede tener menos de 10. Cuando obtenemos números con el formato e-15 (descrito anteriormente), el valor toma entre 11 y 12 posiciones. Por lo tanto, a 10 agregamos otro deuce.
4 es responsable del número de columnas (x, y1, y2, y3), y 5 es el número de caracteres que limitan la celda en una fila.
El resto de las variables parecen ser intuitivas, así que pasemos a imprimir la placa
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
Si conectamos todo el código que ya escribimos, en la consola veremos esto:
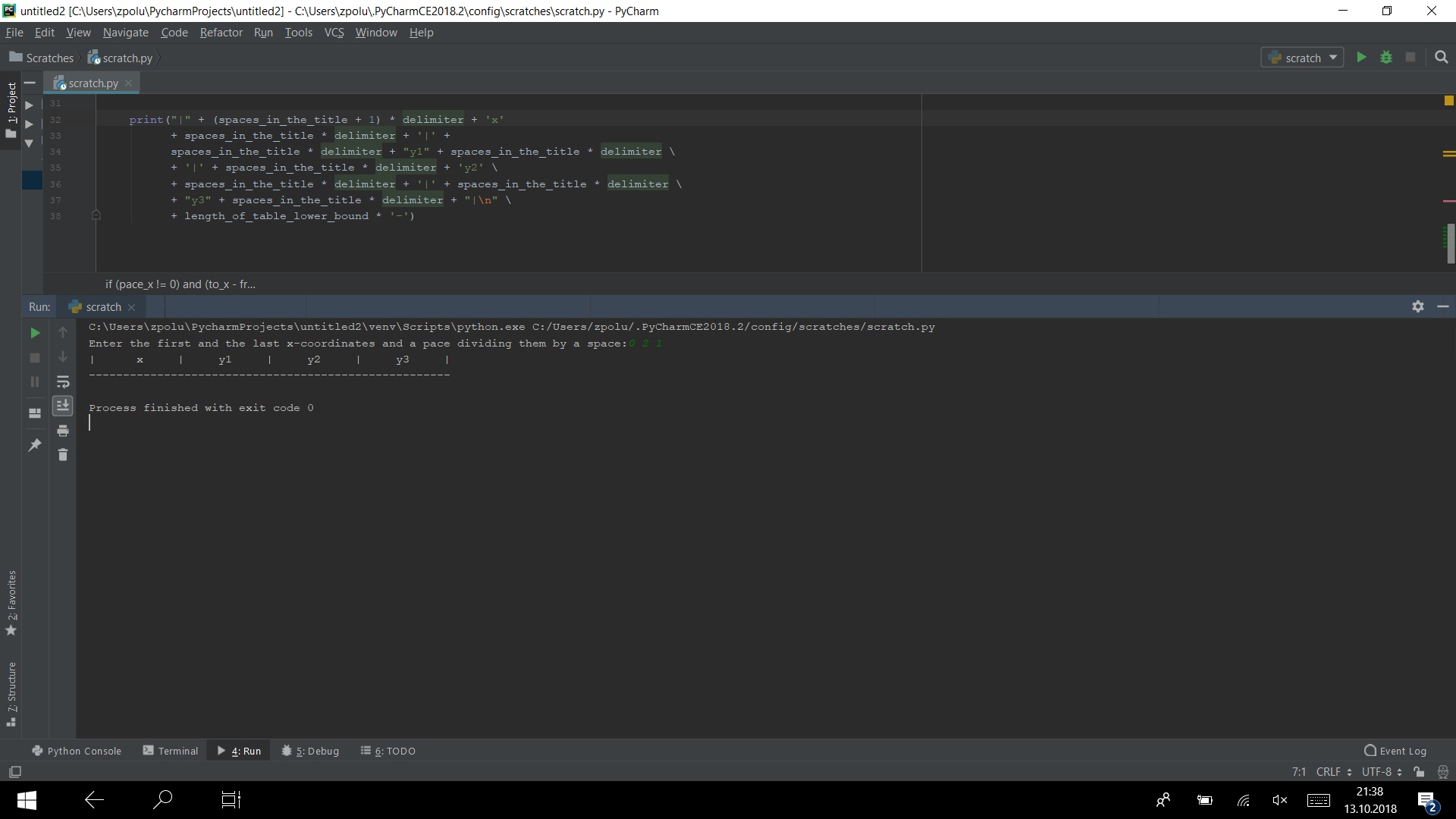
Ahora necesitamos imprimir los valores mismos. Para hacer esto, necesitas un bucle. Dado que los datos ingresados pueden ser fraccionarios, el uso del
rango no funcionará, por lo que usaré un ciclo regular.
Dado que podemos tener tanto una secuencia decreciente de X como una secuencia creciente, las condiciones del ciclo deben establecerse de manera que se tengan en cuenta estas dos opciones. Tenemos una variable creada previamente que almacena la respuesta sobre la naturaleza de la secuencia en forma de 0 o 1. Por lo tanto, es suficiente considerar dos casos y seleccionar la condición apropiada para cada
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
Como para el gráfico necesitamos el mínimo y el máximo del gráfico y1, que dibujaremos, introducimos variables especiales que serán responsables de min y max
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
la construcción, en esencia, repite la construcción de
if: ... else: ... , solo a través de desigualdades booleanas.
y1_cur_value almacena el valor actual de la función. Creé una variable para no llamar constantemente a una función cuando se necesita su valor en un punto.
También necesitaremos la presencia de valores negativos para el trazado.

Ahora imprima directamente los valores. Quiero que todo sea hermoso y centrado en cada una de las celdas, así que tengo que procesar manualmente cada valor para verificar la longitud del número y seleccionar el número de espacios dependiendo de él para alinear el valor.
Nota
Centrar literalmente el número no funcionará. La variable responsable de la precisión tiene el parámetro g. Él dice que un cierto número de posiciones para los números están reservados para un número (en nuestro caso, 10 por defecto). Si no se marcan 10 dígitos, las posiciones en blanco se ubicarán a la izquierda de las posiciones llenas. Por lo tanto, solo podemos centrar una fila de 10 posiciones.
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x : una cadena que ya se ha llevado a una vista con una precisión dada. Ahora necesitamos verificar la longitud del número y seleccionar el número requerido de espacios. Como no se necesita más de un espacio en cada lado, las variables
bool eva son perfectas como guardianas del número de estos mismos espacios.
aux_2 detecta el caso cuando la longitud del número es 11.
También hacemos para los valores de tres funciones
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
Como dije al principio, la segunda y la tercera función tienen puntos de interrupción: ambas funciones no existen en el punto x = 0. Por lo tanto, también necesitamos detectar estos casos.
Bueno, no olvide aumentar el valor actual de x para que no tengamos un ciclo sin fin.
Recopilemos todo el código en un programa y ejecútelo, por ejemplo, en la prueba -1.2 3.6 0.3
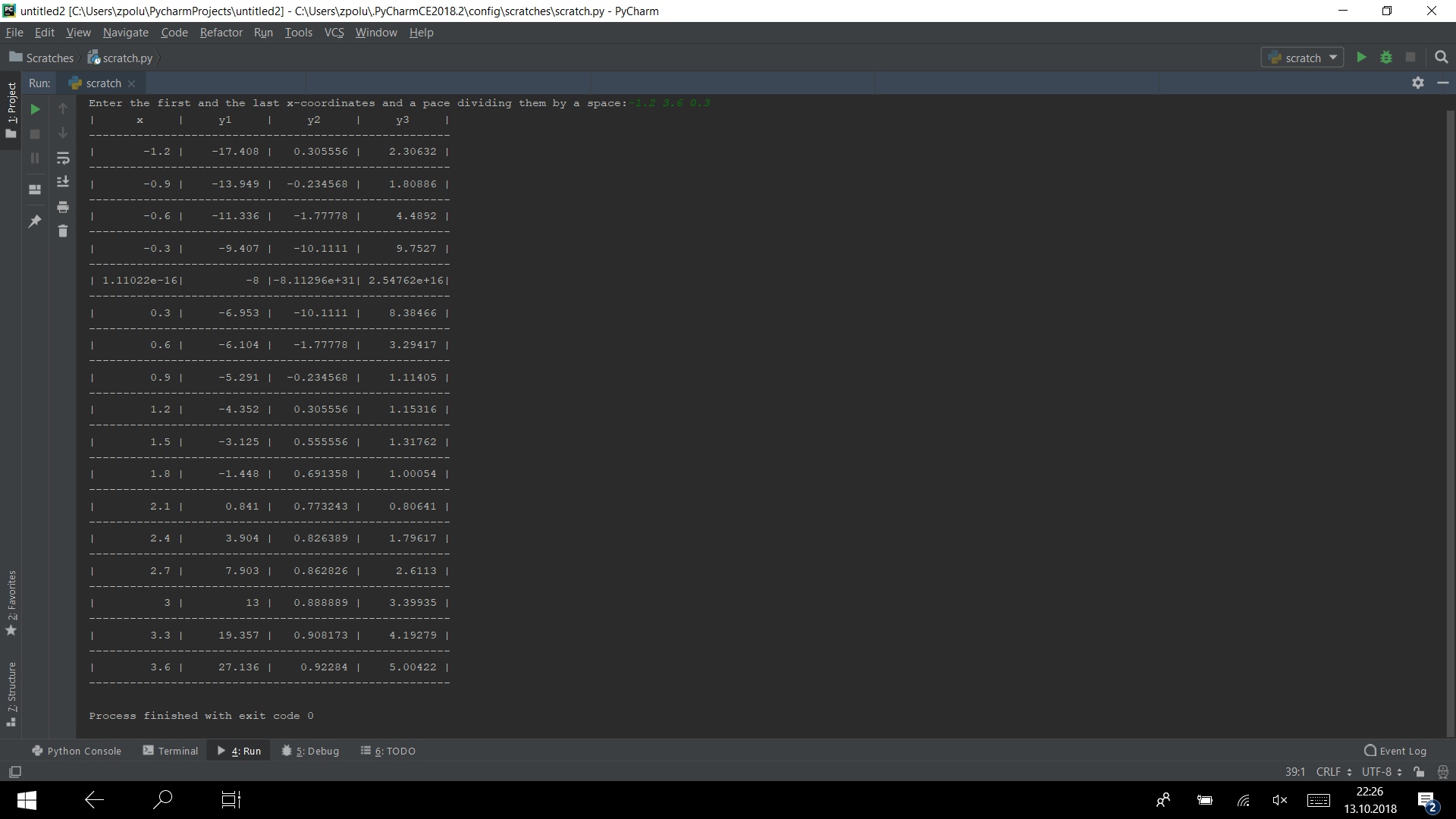
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
En la segunda parte de esta creación, construiremos gráficos
 Continuará ...
Continuará ...