Juego usando tablas de matemáticas en lugar de tablas

En esta captura de pantalla, se te presenta un juego aparentemente normal con gráficos de píxeles. Sin embargo, no todo es tan simple.

El relieve del suelo en algunos lugares se asemeja a una onda sinusoidal, y las balas son similares a dos gráficos simétricos de la raíz de x.

De hecho, todo lo que ves en la pantalla de una forma u otra se relaciona con las matemáticas, las curvas y los gráficos matemáticos.

Antecedentes

Una vez, mientras veía el video del canal "Numberphile", me encontré con un material de video muy interesante llamado "La fórmula de todo" .

En este video, se presentó la fórmula autorreferencial de Tapper , que, con un cierto valor de k, recreó su imagen en el gráfico. Esta fórmula se ve así:

$$

$$\ frac {1} {2} <\ lfloor mod (\ lfloor \ frac {y} {17} \ rfloor 2 ^ {-17 \ lfloor x \ rfloor - mod (\ lfloor y \ rfloor, 17)}, 2 ) \ rfloor$$

Esta fórmula realmente me interesó, y tuve una idea:

"Pero, ¿qué pasa si creas un juego donde en lugar de texturas ordinarias que se almacenan en varios archivos de formato .png y .jpg, se utilizarán gráficos y curvas matemáticas?"

Esta idea me pareció bastante interesante y difícil de implementar.

Las tareas

Me enfrenté a las siguientes tareas:

• Piensa en el significado del juego, jugabilidad
• Derive fórmulas, cuyos gráficos serán las siluetas de personajes, viñetas, superficies que necesito
• Implementa todo esto en el juego

Jugabilidad y significado del juego.

La jugabilidad y el significado del juego cambiaron varias veces durante el desarrollo de este juego. Todo esto se debe a que hubo algunas dificultades, en particular, con la derivación de fórmulas para ciertas siluetas. Pero en general, este juego trata sobre un platillo volador solitario que vuela alrededor de los planetas, los explora y mata a los enemigos que se interponen en su camino.

Fórmulas y su posterior implementación en el juego.

He combinado los dos párrafos siguientes en un subtítulo, porque no es práctico "saltar" entre una fórmula y su implementación.

Para crear el juego, se eligió el lenguaje de programación c ++ y la biblioteca SFML para crear ventanas y dibujar cualquier cosa sobre ellas.

Como estoy en la escuela y recientemente descubrí qué es una sinusoide y cómo se ve, tuve grandes problemas para obtener varias fórmulas. Muy a menudo, esto terminó con una simple selección.

Al final del artículo habrá un enlace a GitHub, donde se publicará todo el código. En el artículo, solo se darán pequeños trozos de código para no tirar basura.

Superficie del planeta

Para la superficie del planeta, deduje la siguiente fórmula:

$$

$$f (x) = | sin (x) |$$

Una fórmula bastante simple, pero cuando se implementó, era necesario controlar la altura y la longitud de una sinusoide dada. Además, para evitar la curvatura del relieve, x se multiplica por π. Por lo tanto, el código final se ve así:

int groundC = ceil(abs(sin(((i+1)*groundScale*M_PI)))*groundHeight); 

Textura del planeta en el espacio

La textura del planeta consiste en un círculo y un patrón en él. El juego tiene 4 fórmulas para crear patrones y 12 texturas de planetas con un patrón diferente. Dependiendo del "paso" de la fórmula, se crean varios patrones. Además, al generar un planeta, se configura de forma pseudoaleatoria para colorear, dimensionar y posicionar en el espacio.

Balas

Imagen de una bala del juego. La bala está vuelta.

Para las viñetas, se eligió una fórmula muy simple:

$$

$$\ sqrt {x}$$

La trama de esta fórmula se refleja en la abscisa.

Protagonista

Entonces llegamos a las fórmulas más complejas.

Deducí la fórmula del protagonista con gran dificultad. Se ve así:

$$

$$\ sqrt {x ^ {\ frac {1} {2.8}} + x ^ {10.9-x ^ {9.3-x}}} - 0.3$$

Sí, una fórmula muy torcida, muy fea. Pero lo principal no es la fórmula, el resultado principal.

Para lograr el resultado, al principio solo quería moverme a lo largo del eje x con un cierto paso, escribir las coordenadas y, y luego conectar todos estos puntos, obteniendo así nuestra placa. Pero luego, accidentalmente di un paso demasiado pequeño, y todo mi plato se alzó maravillosamente con la excepción de dos puntos finales, que finalmente se conectaron. Como resultado, la placa se ve así:



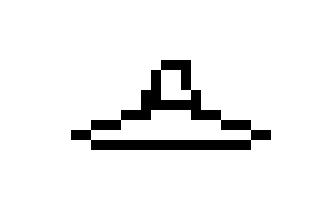
Luego, necesitábamos la textura del protagonista en el espacio. Se ve así:



Se basó en un círculo. La cabina principal se realiza con la siguiente fórmula:

$$

$$(x ^ {7-x}) ^ {\ frac {0.8} {x}}$$

El gráfico de esta fórmula se refleja a lo largo del eje de ordenadas.

Así es como se ve esta fórmula en c ++:

 int x = round(pow(pow(i, 7 - i), 0.8 / i)); 

Enemigos y su engendrador

A la derecha de la imagen hay un generador azul, los objetos rojos son enemigos.

Spauner es un planeta ordinario con un patrón inusual. Este patrón es un gráfico de la fórmula:

$$

$$sin (x) * x ^ {0.8}$$

Fórmula de textura enemiga:

$$

$$(x ^ {3-x}) ^ {\ frac {1} {x}}$$

Arboles

Admito que no pude derivar o seleccionar una fórmula para crear la silueta de los árboles. Pero, para no violar el concepto básico de todo el juego y las reglas de no usar ningún archivo de formato .png y .jpg, utilicé un truco. Usé fractales para crear árboles.


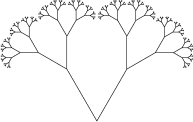Ejemplo de árbol fractal

Lo más probable es que esté de acuerdo en que los árboles fractales se ven bastante aburridos. Si agrega algunos elementos de aleatoriedad, por ejemplo, 2 ramas pueden no necesariamente crecer, sino también 3 o 1, o no crecer. Además, no es posible hacer el mismo ángulo de inclinación en todas partes.

Por supuesto, uno podría hacer un pseudo máquina normal, que se basaba en tics de computadora, pero la siguiente idea me pareció más interesante:

"¿Y si cada árbol recibe un número específico (semilla) a partir del cual se calcularán números pseudoaleatorios que afectan los parámetros del árbol?"

Afortunadamente, c ++ tiene una biblioteca pseudorandum separada.

Como resultado, los árboles generados se ven así:



A la izquierda hay un árbol con semilla 13, y a la derecha - 22

Y el código que genera estos árboles es:

 Branch Branch::createNewBranch(Branch cur, Tree* parent, float angleMultiplier, int level) { Vector2f sp(cur.startPoint.x, cur.startPoint.y); float randomAngle = ((*parent).getRand() * 15) - 5; float t = cur.thickness * 0.75; float l = cur.length * 0.67; float a = cur.angle + 30*angleMultiplier + randomAngle; sp.y -= (cos((cur.angle-180)*3.1415926 / 180) * cur.length); sp.x += (sin((cur.angle-180)*3.1415926 / 180) * cur.length); Branch gen(sp, t, l, a, level); if (level > 0) { int count = 100 * (*parent).getRand(); if (count >= 25 && count < 80) { //     ,      && count < 80,        ,  . , -          20%  10%,  ,    count<90 (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } if (count >= 80) { //    ,    count >= 90 if (count % 2 == 0) { (*parent).addBranch(gen.createNewBranch(gen, parent, -1, level - 1)); } else { (*parent).addBranch(gen.createNewBranch(gen, parent, 1, level - 1)); } } } return gen; } 

Nota Sí, sé que "codifiqué" algunas variables, pero no me culpes por esto. Pensé que no tenía sentido crear variables constantes separadas, que en principio solo afectan la posibilidad de crear una nueva rama.

Un poco más de código

Arriba, proporcioné código solo para generar texturas. En este subtítulo, describiré el código del juego en sí. Todo el código está en GitHub, el enlace al proyecto está en conclusión.

Jugador

El reproductor tiene dos métodos de actualización diferentes: spaceUpdate y planetUpdate. En consecuencia, spaceUpdate actualiza el reproductor cuando está en el espacio, planetUpdate, cuando está en el planeta. En el planeta, se calculan la aceleración y la velocidad del jugador. Dependiendo de la aceleración horizontal, el ángulo de inclinación de la placa cambia de 30 grados a -30. Al acercarse a las barreras, la velocidad del jugador disminuye. Dichas barreras existen para el eje x (0; mapSize.x) y para el eje y. Para el eje y, las cosas son un poco más complicadas. Hay una altura mínima, que se calcula de la siguiente manera: se toma la altura mínima de la tierra, se agrega a la altura de la onda sinusoidal y se agrega la altura de los árboles. La altura de los árboles se calcula de una manera muy simple: la longitud inicial de la rama multiplicada por el número de ciclos realizados durante la generación del árbol. No hay borde superior: al volar fuera del mapa desde arriba, el jugador cambia a spaceUpdate y se dibuja el espacio.

SpaceUpdate funciona de la siguiente manera: se calculan la aceleración y la velocidad del jugador. A continuación, se calcula el ángulo de rotación del jugador. El ángulo se calcula de la siguiente manera: si la aceleración es cero, entonces el ángulo se calcula en relación con la velocidad del jugador, si no, en relación con la aceleración. Además, en el espacio, el jugador tiene la posibilidad de disparar. El disparo se produce de la siguiente manera: se crea una viñeta con una rotación como la de un jugador y se agrega a la lista. Al actualizar un jugador en el espacio, cada viñeta en esta lista también se actualiza. Al representar a un jugador, también se dibujan viñetas. Además, en el espacio, las cosas son un poco más complicadas con las barreras. El espacio se divide en sectores, en cada sector 4 planetas, en total: 1 000 000 planetas y 25 000 sectores. Cada sector tiene una identificación única. Si el resto al dividir por 500 es igual a 0 - hay una barrera izquierda, si el resto de 499 es correcto, si al dividir por 500 el resultado es 0 - la barrera superior está presente, si 499 es la superior. Si no hay barreras, entonces, al volar fuera del cuadro, el jugador se mueve al sector correspondiente.

Espacio

Ya he esbozado la mayor parte, pero aún quedan algunas cosas. En cada uno de los sectores del espacio hay 4 planetas. Cuando un jugador presiona la tecla E, si está a un radio de distancia de este planeta, entonces el jugador se mueve al planeta.

Enemigos

La IA de los enemigos es muy estúpida: si hay un jugador en el radio de su visibilidad, simplemente tienden a chocar contra él y hay un pequeño error, por lo que su camino es una curva bastante. Si no hay ningún jugador en el radio de su visibilidad, entonces son enviados a su generador.

Engendrador

En cada sector del espacio hay 1 generador. Los spauners pueden ser de diferentes tamaños. El tamaño afecta la visibilidad del jugador. Si el jugador está en su zona de visibilidad, el generador crea enemigos cada 5 segundos, pero el número de enemigos no puede exceder los 10.

Conclusión

Después de pasar aproximadamente una semana, creé un juego que no usa ningún archivo .png o .jpg.

Enlace al proyecto en GitHub

Para aquellos que son demasiado flojos para descargar el proyecto y ejecutar el juego, un video corto sobre el juego: