
Continuamos conociendo al muy joven, pero increíblemente bello y poderoso lenguaje de programación Julia . La versión beta de seis años finalmente ha finalizado, por lo que ahora no puede temer los cambios de sintaxis. Y mientras todos discuten si es bueno o malo comenzar a indexar a partir de uno, la comunidad agitada está jugando activamente: están surgiendo nuevas bibliotecas, se están actualizando las antiguas, están comenzando proyectos serios y los estudiantes están enseñando activamente este idioma en las universidades. ¡Así que no nos quedemos atrás! ¡Hacemos el té más fuerte, porque codificaremos esta noche!
Preparación para el trabajo
Aquí hay una pequeña revisión en ruso, también en el centro hay un conocimiento del idioma y las instrucciones de instalación . Una vez más, centrándonos en la necesidad del Marco de administración de Windows , habrá problemas con la descarga de paquetes.
Después de la actualización, JuliaPRO ahora solo incluye a Juno . Pero personalmente me gusta más Jupyter : no hubo problemas con él en la computadora portátil, además es conveniente trabajar en el navegador e inmediatamente crear notas y fórmulas, en general, ideal para crear informes, diapositivas o manuales.
Casarse con Jupyter y Julia 1.0.1 Hay varios paquetes para Julia, los más exitosos se incluyen en los gráficos como backends. Plots.jl : metalenguaje de Plots.jl : es decir, una interfaz para varias bibliotecas de gráficos. Por lo tanto, Plots.jl realidad solo interpreta sus comandos y luego crea gráficos usando algún tipo de biblioteca de gráficos. Estas bibliotecas de gráficos de fondo se denominan backends. La mejor parte es que puede usar muchas bibliotecas de gráficos diferentes con la sintaxis Plots.jl , ¡y también veremos que Plots.jl agrega nuevas características a cada una de estas bibliotecas!
Instalar paquetes gráficosPara instalar paquetes, ejecute los comandos en REPL, Juno o Jupyter:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
No es necesario instalar todos los paquetes, pero debe saber que cada uno de ellos tiene sus propias características . Prefiero plotlyjs () : aunque no difiere en velocidad, es muy interactivo. Hay un zoom que se mueve a lo largo del plano, así como la capacidad de guardar el archivo, y si guarda el documento Jupyter como html, se guardarán todas las características. Para que pueda agregar al sitio o hacer una presentación interactiva. Más información en las páginas: Parcelas , Gadfly
Patrón principal sin fin
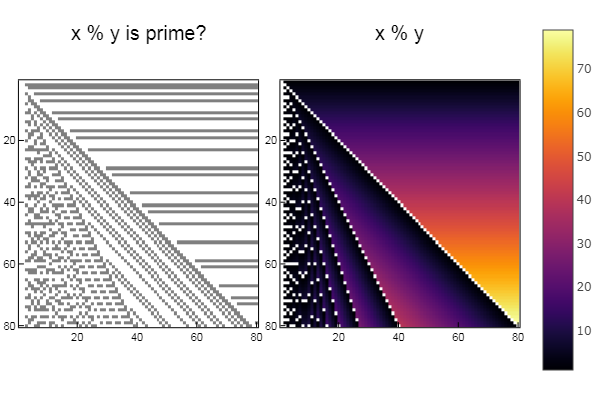
Implementó la idea de un artículo sobre Habr . En pocas palabras: ¿qué pasa si tomamos la coordenada del punto y usamos una operación, por ejemplo, XOR o AND bit a bit entre la abscisa y la ordenada, y luego verificamos el número por simplicidad o por pertenecer a los números de Fibonacci, y si la respuesta es sí, llene el punto con un color, y con un negativo en otro? Comprobar:
Para operación% using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
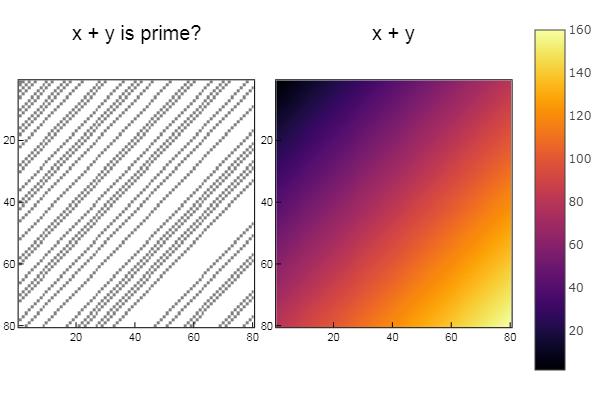
Para operación + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
Para la operación | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

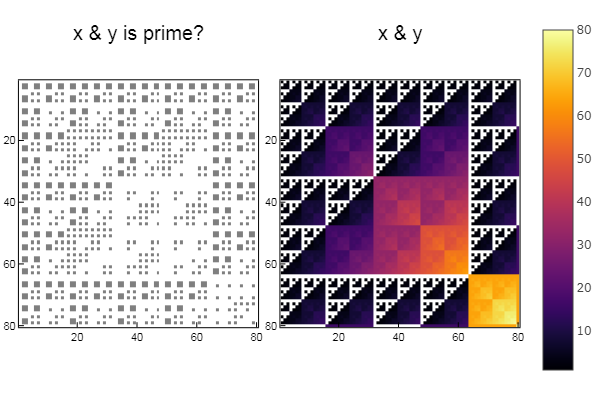
Para la operación y W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
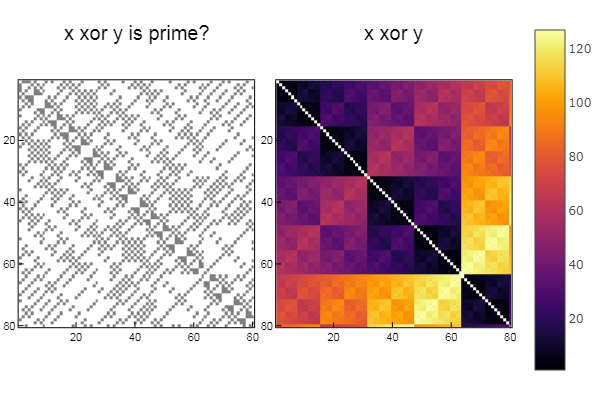
Para la operación xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
Y ahora todo es igual, pero para los números de FibonacciPuedes hacer una serie como de costumbre con algo como:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
Pero usemos la representación matricial (con más detalle ):
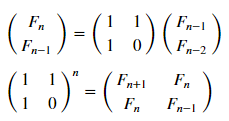
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
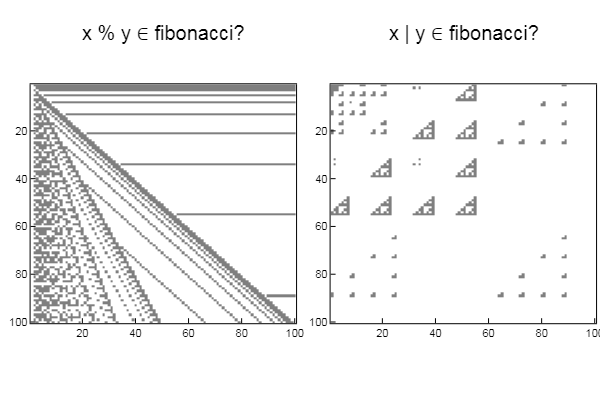
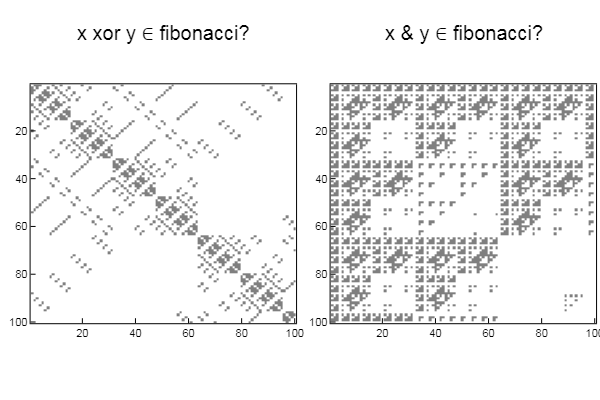
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
Reflexión de una figura relativamente recta
Este tipo de visualización está determinado por la matriz:
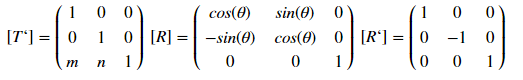
donde [T '], [R] y [R'], respectivamente, las matrices de desplazamiento, rotación y reflexión. Como funciona Analicemos un ejemplo de un desplazamiento: para un punto con coordenadas (x, y), el desplazamiento por m por x y por n por el juego estará determinado por la transformación:
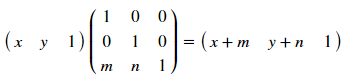
Estas matrices permiten transformaciones para varios polígonos, lo principal es registrar las coordenadas una debajo de la otra y no olvidarse de la columna de la unidad al final. Así [T]:
- desplaza la línea en el origen junto con el polígono que se transforma
- lo gira para que coincida con el eje X
- refleja todos los puntos del polígono con respecto a X
- seguido de rotación inversa y transferencia
El tema se describe con más detalle en el libro Rogers D., Adams J. Mathematical Foundations of Computer Graphics
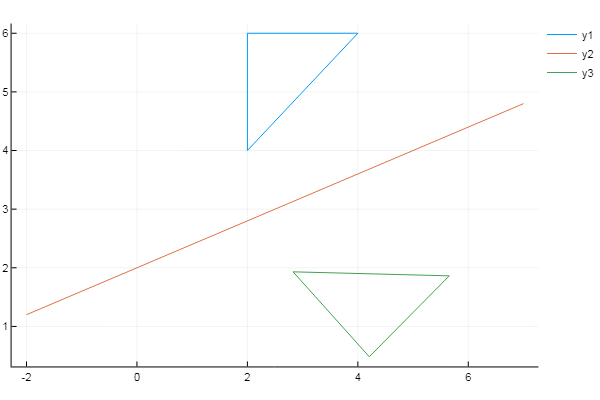
¡Ahora codifícalo!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
Dato interesante: si se deshace de los caracteres griegos y reemplaza la primera línea con
function y=f(x,t) y=0.4*x + 2 endfunction,
Dado que los corchetes [] enmarcan los índices de las matrices en () y las balsas en el plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) , este código se ejecuta prácticamente en Scilab .
Trabaja con gráficos tridimensionales.
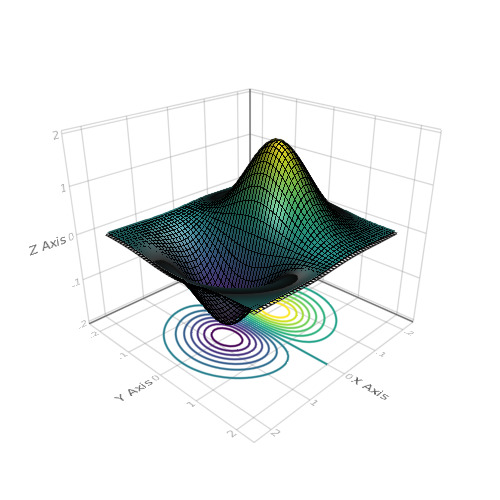
Algunos de estos paquetes admiten la construcción de gráficos tridimensionales. Pero me gustaría mencionar por separado la herramienta de visualización bastante potente de Makie , que funciona en conjunto con los paquetes GLFW y GLAbstraction que implementan las funciones de OpenGL en julia. Más información sobre Makie . Escondemos su aprobación bajo
spoiler using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
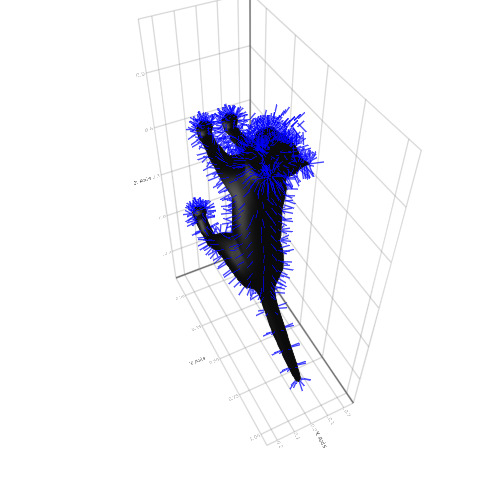
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
Eso es todo con los gráficos. Interactividad, animación, 3D, big data o construcción rápida de gráficos simples: los paquetes en constante evolución satisfarán casi cualquier gusto y necesidad, además, todo es muy fácil de aprender. ¡No dudes en descargar ejercicios prácticos y seguir comprendiendo a Julia!
UPD: Todos los listados anteriores están hechos en Jupyter con julia 0.6.4. Desafortunadamente, algunas funciones del metapaquete Plots se eliminaron o cambiaron de nombre, por lo que seguimos monitoreando las actualizaciones, pero por ahora el espía se reemplaza por completo:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)