Comience comenzó
La última vez decidí construir una tabla de valores de funciones. Ha llegado el momento de proceder con la construcción del programa en sí, para lo cual, de hecho, todo esto comenzó.
Entonces, la idea principal es la siguiente. Gire el eje de coordenadas 90 grados en sentido horario. Esto es necesario para simplificar la construcción sin almacenar datos sobre cada punto en ninguna hoja.
A continuación, limitamos el eje de coordenadas del juego a 82 caracteres para una mejor legibilidad de la tabla. Está claro que al hacerlo perdemos precisión y el cronograma será más esquemático (demasiado apretado), especialmente para funciones "geniales", pero aún así.
Después de eso, calculamos la posición del eje x con respecto al eje de los jugadores, es decir, observamos dónde tendremos un punto (x, 0). Bueno, entonces asignaremos línea por línea x el valor de la función y1 en este punto.
Vamos
Primero, necesitamos la siguiente fórmula:
Asignaremos 80 puestos al horario en sí, los dos lugares restantes serán puramente decorativos. Con esta fórmula, encontramos qué rango de valores corresponde a una posición en nuestro gráfico. Entonces podemos marcar correctamente el punto actual en él.
Se resumen las ideas principales, así que pasemos al código mismo
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Incluyendo gracias a los comentarios a la primera parte, aprendí sobre el
formato . Me pareció realmente más conveniente que mis bailes con una pandereta, por lo que un gran código de cálculo de sangría se convirtió en un par de líneas
print("{1:>{0}}".format(len(label) + dial_length, label), '\n')
La unidad es responsable del número del elemento pasado como argumento para la función de formato, es decir, es un "enlace" (no literalmente) a la variable de etiqueta, que en realidad mostramos en la pantalla. La numeración va exactamente igual que en las hojas, desde cero.
Un par de caracteres
:> se usa para alinear el texto mostrado en el lado derecho. Bueno,
{0} después del carácter
> es necesario para determinar el número de posiciones de línea que necesita.
Es decir, en este caso, reservamos para la etiqueta de línea len (etiqueta) + posiciones dial_length, y la etiqueta en sí solo toma len (etiqueta), y alineamos el texto en el lado derecho dentro del conjunto de estas posiciones.
print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print(dial_length*' ' + label, '\n')
estas lineas son equivalentes
Sí, para las cadenas, es probable que sea más fácil usar la segunda opción, pero aplicar la primera para el desarrollo general no afectará)
print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Incluso las matrices del tipo r_value (en C ++) se pueden agrupar en formato, es decir, crear directamente al pasar un argumento.
Arreglamos las variables que son constantes con nosotros, es decir, no dependen del valor actual de la función.
En python no hay
constantes condicionales para designar constantes, por lo que es habitual llamar a tales variables en mayúsculas y simplemente no cambiarlas.
MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81
Como RATIO por razones obvias no puede ser igual a 0, MAX_Y1_VALUE_DIFFERENCE debe ser un número positivo. Es por eso que el segundo término está en el lado derecho de la tarea.
La posición del eje x que calculamos mediante la fórmula
¿De dónde viene esta fórmula? Simplemente calculamos la relación de los segmentos (en el eje del juego) desde el principio del eje (min (y1)) hasta el valor actual de la función (y1 (x)) y el segmento desde el principio del eje hasta su final (max (y1)). Bueno, multiplicamos esta relación por 80 para encontrar la distancia desde el comienzo del eje hasta el valor actual en espacios (por lo tanto, solo puede usar enteros), lo que reflejará la fórmula de la relación en el gráfico.
Como estamos interesados en la posición en y1 (x) = 0, sustituimos los valores necesarios y listo en la fórmula.
Ahora puede ir directamente a imprimir valores
while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE)
El ciclo ya nos es familiar. Tendremos que contar cada valor de la función por segunda vez, para no almacenarlos en una hoja u otra cosa.
La posición del juego se calcula mediante la fórmula anterior.
Tendremos que corregir la diferencia superior de la fórmula, teniendo en cuenta el caso cuando en la fórmula obtenemos la incertidumbre de la forma cero por cero. Si surge tal incertidumbre, significará que el valor actual es y1 (x) = max (y1), lo que significa que el valor actual del juego coincidirá con el final del eje y.
print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Esta parte del código es directamente responsable de imprimir el gráfico en sí.
print("{1:^{0}.6g}".format(dial_length, from_x), end='')
Aquí, el formato fue muy útil y simplificó el código.
^ nos permite alinear el número en el centro del área seleccionada (en este caso, 12 posiciones).
g es responsable de los números: si no tienen una parte fraccionaria, no se imprimirá (número como int); de lo contrario, 6 decimales
Dado que nuestro gráfico está limitado a un espacio de 80 caracteres a lo largo del eje y, en nuestro gráfico el valor de la función en el punto coincidirá con el eje x no solo en el caso y1 (x) = 0, sino también en la vecindad [0 - RATIO / 2, 0 + RATIO / 2].
En total, tenemos tres casos de la ubicación del asterisco (es decir, el punto) y el palo vertical (es decir, el eje x): '* |' (y1 (x) <= 0 - RATIO / 2), '*' (0 - RATIO / 2 <y1 (x) <0 + RATIO / 2), '| *' (y1 (x)> = 0 + RATIO / 2), consideraremos estos tres casos.
- y1 (x) <= 0 - RELACIÓN / 2
En este caso, el punto está ubicado en el eje x, por lo que estamos buscando la distancia desde el punto al eje en espacios. Debido al redondeo de los números, puede suceder que los valores de las variables AXIS_X_POS y pos_of_y puedan coincidir. Pero esto no puede ser, ya que en este caso estaríamos en el tercer caso. En nuestro caso, el punto no coincide con el eje x, por lo tanto, es necesaria una condición adicional, que reducirá en 1 la variable pos_of_y en caso de igualdad. - y (x)> = 0 + RATIO / 2
El caso es idéntico al primer caso, solo el punto se ubicará en el otro lado del eje x y todas las acciones anteriores se ajustan para esto - el resto
El caso más simple: simplemente imprima un asterisco en lugar del eje
Es decir, si tenemos valores negativos (y1 (x) <0). Si no, simplemente escriba '|' y determinar la posición del punto.
Bueno, terminamos el programa con un eje x adicional.
Entonces, el código que terminó:
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:^{0}.6f}".format(dial_length, x_copy)) print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 81, 'y' , 82*'-']), end=''); MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Ejecute el programa en varias pruebas
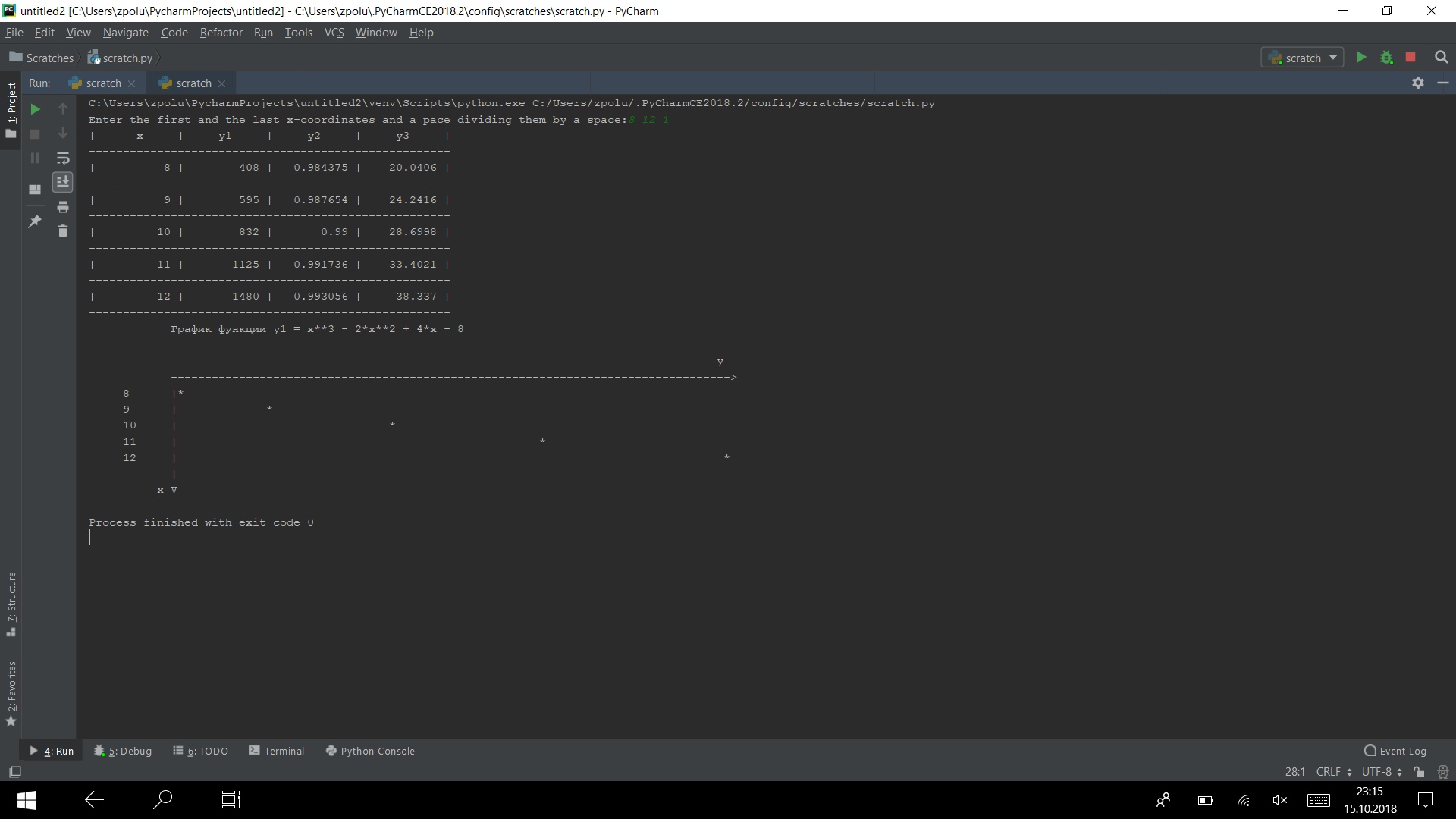
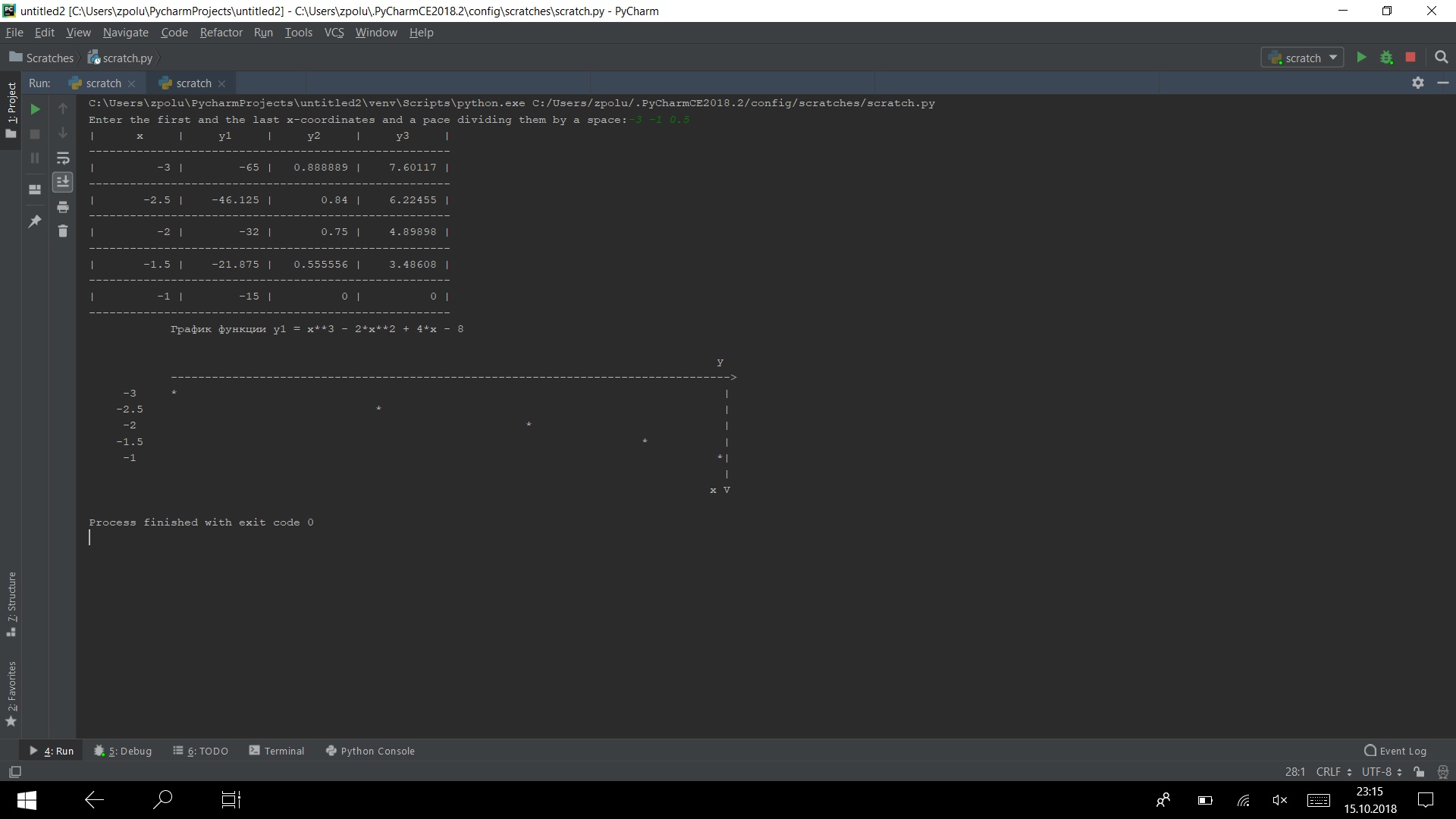
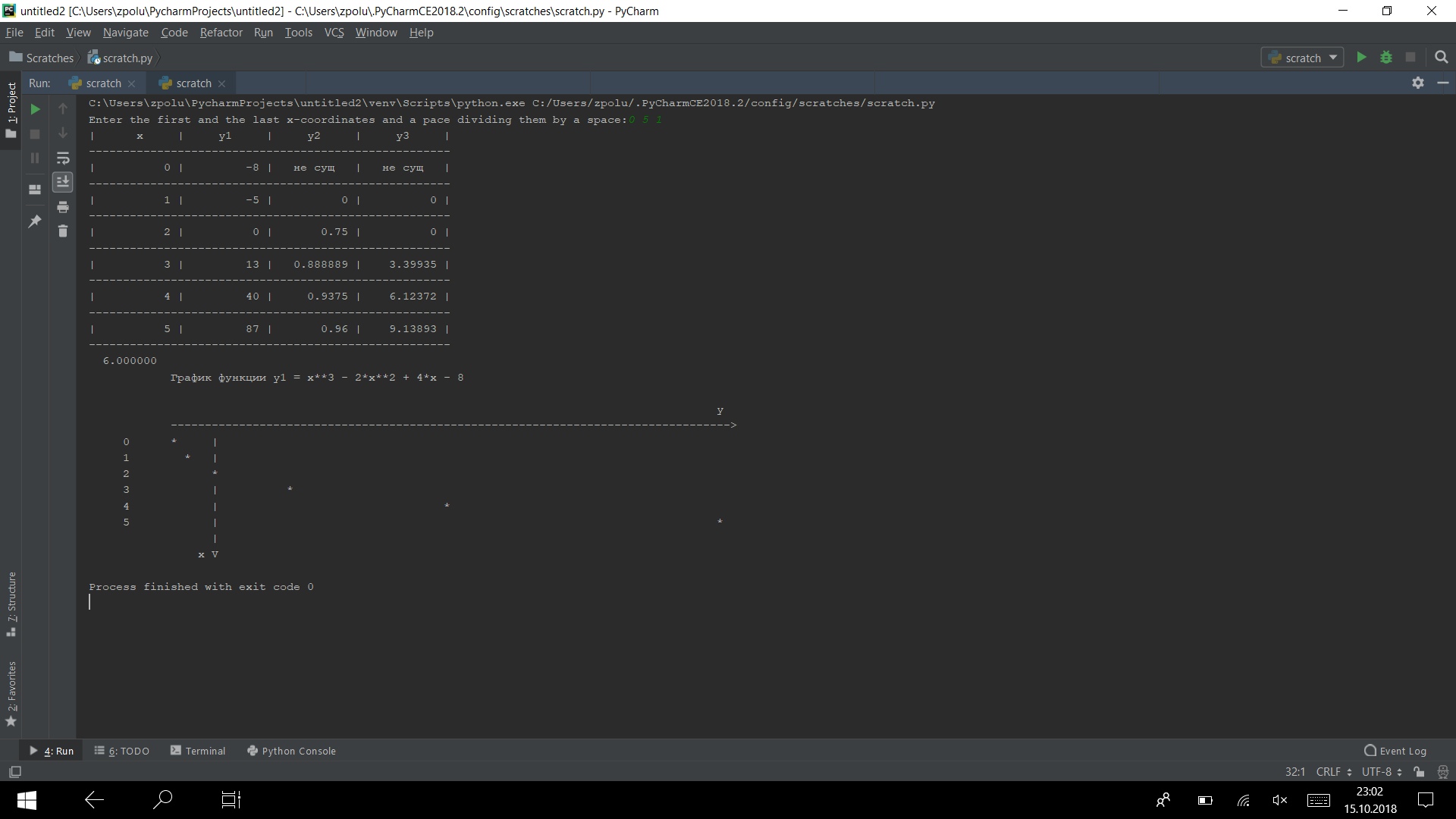
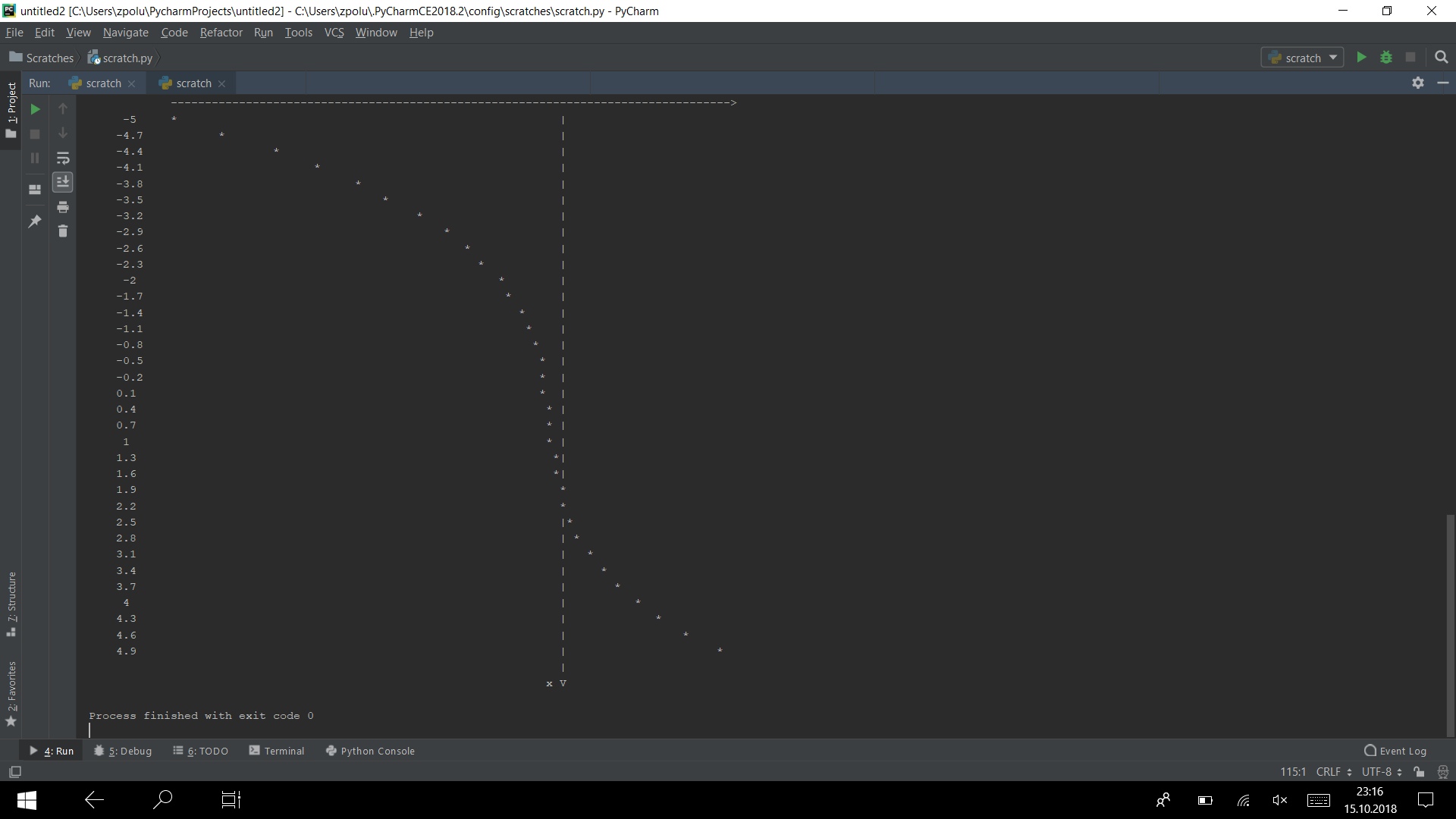
Funciona)
