Espiral giratoria: matemáticas y alucinaciones

Al tratar de imaginar alucinaciones causadas por sustancias narcóticas, me vienen a la mente formas psicodélicas en espiral que se parecen a la visión de túnel . Pero tales estructuras geométricas pueden causar no solo drogas alucinógenas como el LSD, el cannabis o la mescalina . Las personas hablaron sobre la aparición de tales visiones en el momento en que estaban en la muerte, durante condiciones dolorosas como la epilepsia y la esquizofrenia, como resultado de la privación sensorial , o incluso después de una simple presión en los globos oculares. Tales alucinaciones geométricas están tan extendidas que durante el siglo pasado, los científicos comenzaron a preguntarse si podrían decirnos algo fundamental sobre la estructura de nuestro cerebro. Y, al parecer, lo es.


Constantes de forma creadas en una computadora. Las dos imágenes superiores imitan el embudo y la espiral que ocurre después de recibir LSD. La esquina inferior izquierda es el panal creado por la marihuana. La esquina inferior derecha es la web.

Las alucinaciones geométricas sistemáticas comenzaron a ser investigadas por primera vez en la década de 1920 por un psicólogo estadounidense-alemán, Heinrich Kluver . El interés de Kluver en la percepción visual finalmente lo llevó a experimentar con el peyote , un cactus, celebrado por Carlos Castaneda , cuyo ingrediente psicoactivo, la mescalina, jugó un papel importante en los rituales chamánicos de muchas tribus centroamericanas. La mescalina es bien conocida por causar vívidas alucinaciones visuales. Usando peyote en el laboratorio con un asistente, Kluver notó la repetición de formas geométricas en alucinaciones causadas por la mescalina, y las dividió en cuatro tipos, llamándolos constantes : túneles y embudos, espirales, celosías, que incluyen panales y triángulos, y telarañas.

En la década de 1970, los matemáticos Jack Cowan y Bard Ermentraut usaron la clasificación de Kluver para crear una teoría que describe lo que sucede en el cerebro cuando nos hace creer que vemos patrones geométricos. Su teoría fue desarrollada por otros científicos, incluido Paul Breslov, profesor de neurobiología matemática y computacional en el recientemente fundado Centro Oxford de Matemática Aplicada Colaborativa.

¿Dónde están las tiras de la corteza cerebral *

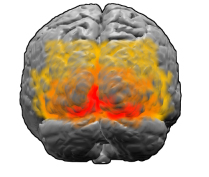La corteza visual. Área marcada en rojo V1

[ * Referencia al cuento de hadas vietnamita "¿De dónde viene el tigre de la tira" / aprox. perev. ]

La primera área de la corteza visual del cerebro que procesa imágenes en humanos y mamíferos es el área conocida como V1. La evidencia experimental, como las imágenes de fMRI , sugiere que los patrones de Kluver también provienen principalmente de V1 y no aparecen más adelante en algún lugar del sistema visual. Al igual que el resto del cerebro, V1 tiene una estructura compleja, arrugada y doblada; sin embargo, hay una forma sorprendentemente directa de traducir lo que vemos en nuestro campo de visión en la actividad de las neuronas en V1. "Imagina que estamos implementando V1", dice Breslov. - Se puede imaginar como un tejido nervioso de varios milímetros de grosor, con varias capas de neuronas. En una primera aproximación, las neuronas a lo largo de la profundidad de la corteza se comportan de manera similar, por lo que si las aplana, puede imaginar V1 como una lámina bidimensional ".

El objeto o escena del mundo visual se proyecta en forma de imagen bidimensional sobre la retina de cada ojo, por lo que lo que vemos también puede considerarse como una hoja plana: campo de visión. Cada punto en esta hoja puede ser designado por dos coordenadas, como un punto en el mapa, o un punto en un modelo plano V1. Las áreas alternas de luz y oscuridad que componen las alucinaciones geométricas son causadas por las áreas alternas de alta y baja actividad de las neuronas en V1, áreas donde las neuronas se activan muy rápidamente y áreas donde ocurre lo contrario.

Para traducir los patrones visuales en actividad neuronal, es necesaria una cuadrícula de coordenadas, una regla según la cual cada punto del campo de visión está conectado con un punto del modelo plano V1. En la década de 1970, los científicos, incluido Cowen, crearon una cuadrícula basada en el conocimiento de la anatomía de la interacción de las neuronas retinianas con las neuronas en V1. Para cada porción clara u oscura del campo de visión, el mapeo define una porción de actividad neuronal alta o baja en V1.

¿Cómo transforma esta imagen de la retina y la corteza los patrones geométricos de Kluver? Resulta que las alucinaciones, que causan espirales, círculos y rayos que emanan del centro, corresponden a las tiras de actividad de las neuronas en V1 que pasan en ángulos dados. Los enrejados como los panales o las células corresponden a los patrones hexagonales de actividad en V1. Esto en sí mismo puede no ser tan interesante, pero hay un precedente: fueron las rayas y los hexágonos que los científicos observaron al modelar otros ejemplos de la formación de patrones, por ejemplo, convección de líquidos o, lo que es más sorprendente, la aparición de manchas y rayas en las pieles de animales. La matemática que rige la formación de estos patrones era bien conocida, y también propuso un mecanismo para modelar el funcionamiento de la corteza visual.

Del campo de visión a la corteza visual

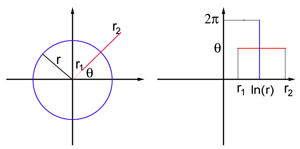
Imagine el campo de visión en forma de una hoja plana con coordenadas polares: cada punto P está definido por dos números, (r, θ), donde r es la distancia al origen y θ es el ángulo entre el segmento OP y el eje x. El punto de referencia corresponde al centro del campo de visión. V1 también se modela como una hoja plana, pero esta vez con coordenadas cartesianas (x, y). La visualización de coordenadas exactas del campo de visión y el modelo plano V1 es demasiado complicada para este artículo, pero para puntos lo suficientemente lejos del centro del campo de visión (es decir, para una r suficientemente grande) se asemeja a un mapa logarítmico:

$$

$$x = \ ln {r} \\ y = \ theta$$

El mapeo traduce un círculo de radio r en el campo de visión en un segmento vertical recto con x = ln r, y un rayo que proviene del origen de las coordenadas O en un ángulo θ en un segmento horizontal recto con y = θ

¿Dónde ve el leopardo?

El primer modelo para formar patrones de piel animal se remonta a Alan Turing , mejor conocido como el padre de la informática moderna y un hacker de Bletchley Park que descifró códigos. Turing estaba interesado en cómo un sistema espacialmente homogéneo como una bola de células uniforme, que es el embrión del animal, puede crear patrones espacialmente no homogéneos, pero estáticos, como las rayas de cebra.

Turing sugirió que estos patrones aparecen como resultado de un proceso de reacción-difusión . Imagine un embrión animal en cuya piel viven dos compuestos químicos. Uno de ellos es un inhibidor que suprime la producción de sí mismo y de otro químico. El otro es un catalizador que provoca la producción de ambas sustancias.

En el momento inicial del modelo de Turing, dos productos químicos se equilibran idealmente entre sí: están en equilibrio y su concentración en diferentes puntos del embrión no cambia con el tiempo. Ahora imagine que por alguna razón, en un punto, la concentración de catalizador aumentó ligeramente. Esta ligera perturbación pone en marcha todo el sistema. El aumento de la concentración local del catalizador significa que allí se producen más catalizador e inhibidor. Sin embargo, ambos compuestos también se difunden sobre la piel del embrión, inhibiendo y catalizando su producción en otros lugares.

Por ejemplo, si un inhibidor se difunde más rápido que un catalizador, rodeará rápidamente el punto de perturbación y reducirá la concentración de catalizador en él. Como resultado, obtenemos una sección con una alta concentración de catalizador, rodeada por una alta concentración de inhibidor; en otras palabras, una mancha de catalizador en el fondo del inhibidor. Dependiendo de la velocidad de difusión de los dos compuestos, es posible que tal patrón manchado aparezca en toda la piel del embrión y finalmente se estabilice.

Thuring escribió un sistema de ecuaciones diferenciales que describe la competencia entre los dos compuestos: puede dejar que se desarrollen a tiempo y ver si aparecen patrones. Estas ecuaciones dependen de parámetros que describen la velocidad de difusión de dos compuestos: si los selecciona correctamente, el sistema eventualmente se estabiliza, formando un cierto patrón que puede cambiarse cambiando los parámetros. El enlace proporciona un applet en Java , en el que puede jugar con los parámetros y observar los patrones resultantes.

Ecuaciones de patrones animales

Para simplificar, imagine un embrión en forma de línea unidimensional. En cualquier momento ty en cualquier punto x del embrión, la concentración del catalizador (activador) e inhibidor (inhibidor) está determinada por las funciones A (x, t) e I (x, t). Cambian con el tiempo de acuerdo con las siguientes reglas:

$$

$$\ frac {\ partial A} {\ partial t} = f (A, I) + \ frac {\ partial ^ 2 A} {\ partial x ^ 2} \\ \ frac {\ partial I} {\ partial t } = g (A, I) + d \ frac {\ partial ^ 2 I} {\ partial x ^ 2}$$

El primer término a la derecha de cada ecuación describe la cantidad de producción de catalizador e inhibidor. Son funciones de las concentraciones de catalizador e inhibidor, ya que ambas afectan la velocidad de reacción.

El segundo término a la derecha de cada ecuación es la segunda derivada, que describe la tasa de cambio del gradiente del catalizador y el inhibidor. Establecen la velocidad de difusión.

Un término adicional d en el lado derecho de la segunda ecuación es el coeficiente de difusión, que muestra cuánto difunde el inhibidor más rápido que el catalizador. Turing ha demostrado que la superioridad en la velocidad del inhibidor es un parámetro crítico para la generación de manchas.

Patrones cerebrales

La actividad de las neuronas en el cerebro no es un proceso de reacción difusa, sin embargo, tiene analogías con el modelo de Turing. "Las neuronas se envían señales entre sí a través de canales de salida de datos llamados axones", dice Breslov. Las neuronas reaccionan a las señales del otro, aquí está la reacción. "Las señales viajan tan rápido en comparación con el proceso de creación de patrones que pueden confundirse con interacciones instantáneas". Por lo tanto, en lugar de difusión, un proceso local, tenemos interacción instantánea a distancia. Las funciones de catalizador e inhibidor son desempeñadas por dos clases diferentes de neuronas. "Hay neuronas excitadoras, que aumentan la probabilidad de que otras neuronas se activen, y hay neuronas inhibidoras que reducen esta probabilidad", dice Breslov. "La competencia entre las dos clases de neuronas es análoga al mecanismo inhibidor del catalizador en el modelo de Turing".


Rayas, patrones hexagonales y rectangulares de actividad nerviosa en V1 generados por un modelo matemático

Inspirados por las analogías de los procesos de Turing, Cowan y Ermentraut crearon un modelo de actividad nerviosa en V1 utilizando un conjunto de ecuaciones formuladas por Cowan y Hugh Wilson. Aunque las ecuaciones resultaron ser más complicadas que las de Turing, todavía puedes jugar el mismo juego, dejando que el sistema evolucione con el tiempo y veas si se desarrollan patrones de actividad nerviosa. "Puede encontrar que, bajo ciertas condiciones, si aumenta el parámetro, que representa, por ejemplo, el efecto de las drogas en la corteza, esto conducirá al crecimiento de patrones periódicos", dice Breslov.

El modelo de Cowan y Ermentraut sugiere que las alucinaciones geométricas son el resultado de la inestabilidad en V1: algo, por ejemplo, la presencia de una droga, elimina la red neuronal de un estado equilibrado, iniciando un proceso de interacción de neuronas excitantes y supresoras, que luego se estabiliza, lo que luego estabiliza en forma de patrones rayados o hexagonales de actividad nerviosa en V1. Luego "observamos" este patrón en forma de estructuras geométricas descritas por Kluver en el campo de visión.

Simetrías en el cerebro

De hecho, no todo es tan simple como en el modelo de Cowan y Ermentraut, ya que las neuronas responden no solo a las imágenes claras y oscuras. Por el grosor V1, las neuronas se alinean en columnas conocidas como hipercolumnas , cada una de las cuales responde aproximadamente a una pequeña porción del campo visual. Pero no todas las neuronas en la hipercolumna son iguales: además de reconocer las áreas claras y oscuras, cada neurona se especializa en reconocer caras locales, líneas que separan las áreas claras y oscuras en una parte de la imagen, una cierta orientación. Algunos reconocen caras horizontales, otros - verticales, otros - caras ubicadas en un ángulo de 45 °, y así sucesivamente. Cada hipercolumna contiene columnas de neuronas de todas las orientaciones preferidas; por lo tanto, una hipercolumna puede responder a las caras de todas las orientaciones en un área determinada del campo visual. Es la composición de las hipercolumnas y las preferencias de orientación que nos permiten reconocer los contornos, las superficies y las texturas del mundo visual.


Conexiones en V1: las neuronas en una hipercolumna interactúan con la mayoría de las otras neuronas. Pero reaccionan con las neuronas en otras hipercolumnas solo si las columnas están ubicadas en la dirección de su orientación, y las neuronas tienen la misma preferencia de orientación.

En los últimos años, se ha recogido una gran cantidad de evidencia anatómica de cómo las neuronas interactúan entre sí con diferentes preferencias de orientación. Dentro de su geocolumna, las neuronas interactúan con la mayoría de las otras neuronas, independientemente de sus preferencias. Pero, en cuanto a las neuronas de otras hipercolumnas, actúan de manera más selectiva, interactuando solo con neuronas de preferencias similares, para garantizarnos la capacidad de reconocer contornos continuos en el mundo visual.

Breslov, junto con Cowan, el matemático Martin Golubitsky y otros científicos, generalizó el modelo original de Cowen y Ermentraut para tener en cuenta estas nuevas pruebas anatómicas. Nuevamente utilizaron el plano como base del modelo V1: cada hipercolumna está representada en el plano por un punto (x, y), y cada punto (x, y) corresponde a una hipercolumna. Las neuronas con una preferencia dada por la orientación θ (donde θ es el ángulo entre 0 y π se denotan por la posición de la hipercolumna (x, y) junto con el ángulo θ, es decir, se denotan por tres unidades de información, (x, y, θ). Los modelos V1 no son un plano, sino un plano con un conjunto completo de orientaciones para cada punto.


Si dos elementos, (x, y, θ) y (s, t, θ) interactúan, entonces otros elementos con la misma orientación interactúan en los puntos (x + a, y + b) y (s + a, t + b ) y elementos con la orientación -θ en los puntos (x, -y) y (s, -t).

Para cumplir con la evidencia anatómica, Breslov y sus colegas sugirieron que la neurona indicada por el punto (x ₀ , y ₀ , θ ₀ ) interactúa con todas las demás neuronas en la misma hipercolumna (x ₀ , y ₀ ). Pero interactúa con las neuronas de otras hipercolumnas solo si se encuentran en su orientación preferida θ ₀ : en el plano, debe dibujar una línea a través del punto (x ₀ , y ₀ ) en un ángulo θ ₀ . Luego, las neuronas denotadas por el punto (x ₀ , y ₀ , θ ₀ ) interactúan solo con las neuronas de las hipercolumnas que se encuentran en la misma línea, es decir, que tienen la misma orientación preferida θ ₀ .

Este esquema de interacción es muy simétrico. Por ejemplo, no cambia cuando el plano se desplaza en cualquier dirección por cualquier distancia: si dos elementos, (x ₀ , y ₀ , θ ₀ ) y (s ₀ , t ₀ , φ ₀ ), interactúan, entonces los elementos obtenidos por el cambio, (x ₀ + a, y ₀ + b, θ ₀ ) y (s ₀ + a, t ₀ + b, φ ₀ ) para algunos ayb, interactúan de la misma manera. Por el mismo principio, el esquema es invariante con respecto a las rotaciones y reflexiones del plano.


Una alucinación reticular creada por un modelo matemático. Se parece mucho a las alucinaciones que ocurren al tomar marihuana.

Breslov y sus colegas utilizaron una versión generalizada de las ecuaciones del modelo original para permitir que el sistema se desarrolle. El resultado es un modelo que no solo es más preciso en términos de la anatomía de V1, sino que también es capaz de generar patrones geométricos en el campo de visión que el modelo original no era capaz de hacer. Esto incluye túneles de celosía, panales y telarañas, cuya orientación de los contornos los caracteriza mejor que las áreas de contraste claro y oscuro.

Además, el modelo es sensible a las simetrías de los esquemas de interacción neuronal: los matemáticos han demostrado que son estas simetrías las que generan la formación de patrones periódicos de actividad nerviosa. Por lo tanto, el modelo supone que las alucinaciones dan lugar a la disposición de hipercolumnas y preferencias de orientación, es decir, mecanismos que nos ayudan a reconocer las caras, contornos, superficies y texturas del mundo visual. Es cuando estos mecanismos pierden estabilidad, por ejemplo, como resultado de la exposición al medicamento, aparecen patrones de actividad que se convierten en alucinaciones visuales.

Más allá de las alucinaciones

El modelo de Breslov no solo permite obtener información sobre los mecanismos que generan alucinaciones visuales, sino que también proporciona pistas sobre la arquitectura del cerebro en un sentido más amplio. Junto con su esposa, un neurobiólogo experimental, Breslov estudió los contornos de las conexiones de las hipercolumnas con visión normal para comprender cómo se procesan las imágenes visuales. “Las personas están acostumbradas a creer que las neuronas en V1 simplemente definen caras locales, y que uno necesita ir a niveles más altos del cerebro para recolectar estas caras y reconocer cosas más complejas como contornos y superficies. Pero de nuestro trabajo con mi esposa está claro que estas estructuras en V1 realmente permiten que la corteza visual reconozca los contornos en una etapa temprana y realice un procesamiento más global. Se creía que procesábamos aspectos cada vez más complejos de la imagen, subiendo más en la jerarquía del cerebro. Ahora quedó claro que hay una retroalimentación activa entre las partes superior e inferior de la corteza."Este no es un simple proceso jerárquico, sino un sistema increíblemente complejo y activo, que llevará muchos años entender".

Entre las aplicaciones prácticas de este trabajo está la visión por computadora: los científicos informáticos ya están construyendo estructuras con conexiones internas con las que jugaron Breslov y sus colegas para construir modelos que enseñen a las computadoras cómo definir contornos y texturas. Si muestra un poco de imaginación, puede imaginar que este estudio algún día podrá ayudar a restaurar la visión de las personas con discapacidad. "La pregunta es si es posible estimular de alguna manera parte de la corteza visual, sin pasar por el ojo, y usar esto para orientar a los ciegos", dice Breslov. "Si comprende cómo está estructurada la corteza y cómo reacciona a la estimulación, quizás entonces sea posible inventar el mejor método para su estimulación correcta".

Incluso hay áreas de aplicación que no están conectadas con el cerebro. Breslov aplicó las ideas obtenidas a través de su trabajo a otras situaciones en las que los objetos se ubican en un espacio con cierta orientación, por ejemplo, fibroblastos de tejidos humanos y animales. Mostró que, bajo ciertas condiciones, estas células y moléculas que interactúan pueden alinearse y producir patrones similares a los que aparecen en V1.

La gente hablaba de ver alucinaciones desde el principio de los tiempos, y en casi todas las culturas, incluso se pueden encontrar imágenes de alucinaciones en los petroglifos.y pinturas rupestres. En las tradiciones de los chamanes de todo el mundo, son tratados como mensajes del mundo de los espíritus. Pocos neurocientíficos modernos estarán de acuerdo con la participación de los espíritus en esto, pero como mensajeros del mundo oculto, esta vez, el mundo oculto de nuestro cerebro, estas alucinaciones no han perdido sus capacidades.