Bicicletas Neuróticas: Génesis

El otro día, Youtube pensó que sería interesante ver un video titulado "AI aprende a jugar Hill Climb Racing". Es curioso, porque un par de minutos antes había cometido los siguientes cambios en el proyecto, donde mis colegas y yo, entre el trabajo y el trabajo, resolvemos este problema. Es cierto que no había "AI" en ese video : el autor entretuvo a la audiencia con indulgencia con Box2D y se calmó al respecto. Sin embargo, propongo considerar este hecho como una prueba convincente de la relevancia del tema y desmontar el dispositivo de nuestro sonajero.

Brevemente sobre la tarea: el vehículo, en nuestro caso es Alien o la máquina de coser Singer sobre ruedas, llamémoslo simplemente "agente", debe conducir a lo largo de las dunas con el mismo nombre de principio a fin. Así es como se ve el agente en su caja de arena:



Un agente que toca la parte posterior de la pista o no muestra un celo adecuado al avanzar hacia la meta es eliminado de la pista.

Resolveremos el problema utilizando redes neuronales, pero optimizado por el algoritmo genético (GA): este proceso se llama neuroevolución . Utilizamos el método NEAT (NeuroEvolution of Augmenting Topologies) inventado por Kenneth Stanley y Risto Miikkulainen a principios de siglo [1] : en primer lugar, trabajó bien en problemas importantes para la economía nacional y, en segundo lugar, comenzamos a trabajar en el proyecto ya tenía su propio marco implementando NEAT. Entonces, francamente, no elegimos un método de solución, sino que elegimos una tarea en la que puede manejar lo que ya está listo.

La figura muestra un esquema aproximado de algoritmos genéticos:



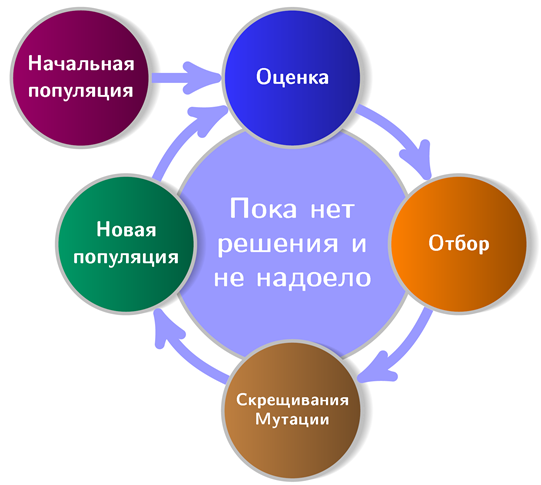
Se puede ver que cualquier GA decente comienza con la población inicial (la población es un conjunto de soluciones potenciales). Nos comprometeremos en su creación y al mismo tiempo nos familiarizaremos con el primer principio de NEAT . Según este principio, todos los agentes en la población inicial deberían tener la topología más simple y "mínima" de la red neuronal. ¿Qué tiene que ver la topología con ella? El hecho es que en NEAT junto con la optimización de los pesos de conexión, la arquitectura de red también evoluciona. Esto, por cierto, elimina la necesidad de su diseño para la tarea. Pasar de arquitecturas simples a complejas no solo es lógico, sino también práctico (hay menos espacio de búsqueda), por lo que debe comenzar con el mínimo de topologías posibles: así es como razonaron los autores del método.

Para nuestro y todos los casos similares, esta topología mínima se deriva de las siguientes consideraciones. Para hacer algo significativo, el agente necesita:

• tener información sobre el medio ambiente y su condición,
• procesar esta información
• interactúa con tu mundo.

El primer papel lo juegan los sensores : las neuronas de la capa de entrada, a las que proporcionaremos información útil para el agente. Las neuronas de la capa de salida procesarán los datos de los sensores. Los actores , dispositivos que realizan acciones mecánicas en respuesta a una señal de "su" neurona de la capa de salida, son responsables de interactuar con el entorno. Por lo tanto, el principio general de la construcción de la configuración inicial es el siguiente: determinamos con sensores y actuadores, iniciamos una neurona por actuador, conectamos todos los sensores y una neurona especial más: una neurona de desplazamiento ( sesgo , a continuación) con pesos aleatorios para todas las neuronas. capa de salida. Algo como esto:



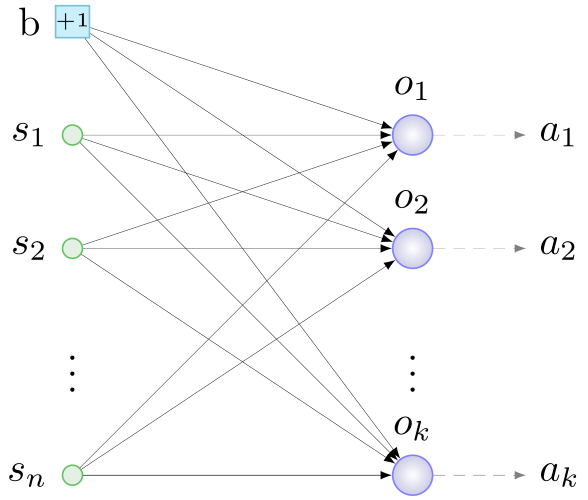b - sesgo, s - sensores, o - neuronas de la capa de salida, a - actuadores, n - número de sensores, k - número de actuadores

Y aquí está el NS mínimo para nuestra tarea:



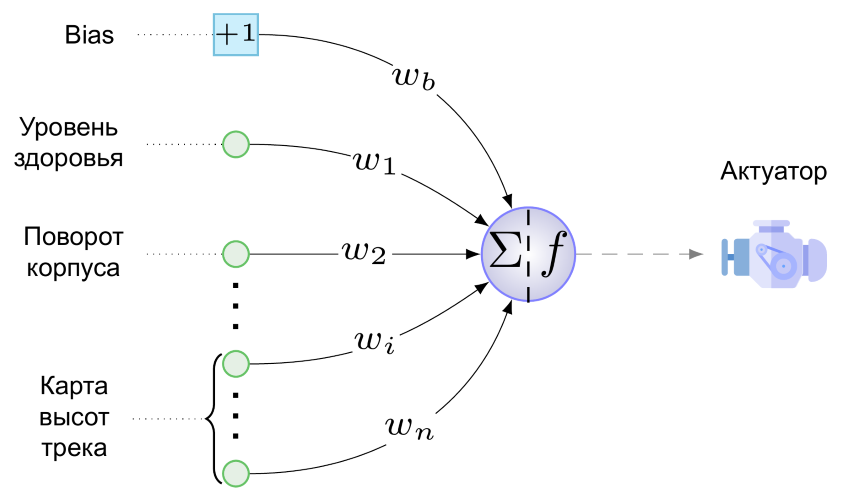
Tenemos un solo actuador: este es el motor de nuestra creación con ruedas. Todavía no sabe cómo disparar, saltar y tocar la tubería. El siguiente valor se proporciona al motor desde una sola neurona de la capa de salida (es una pena llamarla capa):


Aquí w _b es el valor del peso de la conexión que pasa del sesgo a la neurona de salida, multiplicado por el hecho de que cualquier sesgo "produce", es decir +1, s _i es el valor normalizado al rango [0,1] en el sensor i-ésimo, w _i es el valor del peso de conexión desde el sensor i-ésimo hasta la neurona de salida, yf es la función de activación.

Como función de activación, usamos esta fantasía de softsign:


- Ella demostró el mejor rendimiento en las pruebas de un conocido neuroevolucionista en círculos estrechos [2] . Y no tiene sentido comparar la suavidad de las curvas y la simetría de la gráfica de esta función con el LeLy ReLU con curva angular:



Esta figura muestra la reacción del agente a diferentes valores de la función de activación. A valores cercanos a la unidad, el motor hace girar las ruedas en el sentido de las agujas del reloj, acelerando el agente hacia adelante e inclinando fuertemente la carcasa hacia atrás, de modo que los débiles, pero valientes, se vuelcan rápidamente y mueren. Con valores cercanos a 0, lo contrario es cierto, y con un valor de 0.5, el motor del agente no funciona.

La misma figura muestra el papel de la neurona de polarización: el peso del enlace que va de ella a la neurona de la capa de salida es responsable, como se deduce de (1), de la magnitud y dirección de la polarización f (x) a lo largo de la abscisa. La línea de puntos en la figura muestra un gráfico de la función de activación en w _b = -1. Resulta que incluso en ausencia de una señal en los sensores, un agente con dicha conexión retrocederá rápidamente: f (x) = f (-1 + 0) ≈0.083 <0.5. En general, cambiar los valores de la función horizontalmente permite que la conexión de polarización se ajuste sutilmente (bien o de forma gruesa, dependiendo del peso) a la reacción del motor a todos los valores del sensor y al peso de sus conexiones a la vez. Parece que se ha agregado una nueva dimensión al espacio de búsqueda (se deberá buscar el valor "correcto" para w _b ), pero los beneficios en forma de un grado adicional de libertad superan la posibilidad de tales desplazamientos.

Bueno, presentamos las redes neuronales de agentes de la futura población inicial. Pero NEAT es un algoritmo genético, y funciona con genotipos : las estructuras a partir de las cuales se forman las redes o, más generalmente, los fenotipos en el proceso de decodificación. Desde que comenzamos con el fenotipo, haremos todo al revés: intenta codificar la red presentada anteriormente en el genotipo. Aquí no puede prescindir del segundo principio NEAT , cuya esencia principal es la siguiente: en el genotipo, además de la estructura de la red neuronal y los pesos de sus conexiones, la información se almacena en la historia del origen de todos sus elementos. Con la excepción de este aspecto histórico, el fenotipo está codificado en el genotipo casi "uno a uno", por lo tanto, ahora ilustraremos el segundo principio con fragmentos de redes neuronales.

El valor de este principio es difícil de sobreestimar: brinda a los agentes la posibilidad de reproducción sexual. El tema es bastante delicado, por lo que primero consideraremos la reproducción asexual . Sucede así: se hace una copia de todos los genes del agente, se realiza uno de varios tipos de cambios sobre ellos: mutaciones . En nuestra versión de NEAT, son posibles las siguientes mutaciones:

• cambio de peso de conexión
• desvincular
• agregar enlace
• Inserción de neuronas.

Los primeros tres tipos de mutaciones son simples y comprensibles sin más explicaciones. La inserción de una neurona se muestra en la figura a continuación, siempre se realiza en lugar de la conexión existente, la conexión se elimina y aparecen dos nuevas en su lugar:



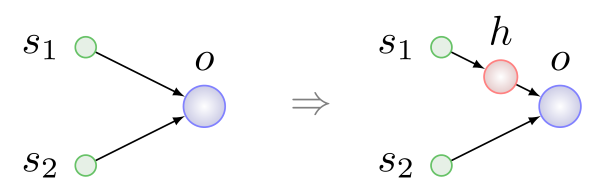
Aquí h es una neurona oculta .

Dos agentes están involucrados en la reproducción sexual o cruces - padres, y como resultado aparece un tercero - un niño. En el proceso de formación del genotipo del niño, se produce un intercambio, digamos, de genes o grupos de genes de padres que tienen un significado idéntico. El segundo principio es justo lo que necesita para buscar genes con el mismo significado.

Imagine que queremos cruzar agentes con genotipos que han sufrido diferentes series de mutaciones de la lista anterior:



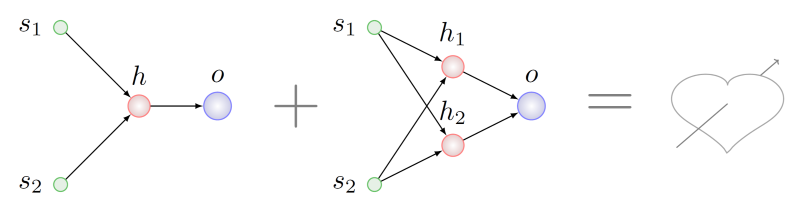
Parece lógico buscar algunos fragmentos que son comunes en términos de topología en ambos padres y tomar un fragmento de estos fragmentos para el genotipo del feto. Será difícil hacer esto, incluso NP es difícil en el caso general, pero supongamos que lo logramos. En este caso, encontramos que en el padre a la derecha hay dos subgrafos isomorfos a la gráfica del padre izquierdo. En la figura siguiente, los arcos de estas subgrafías se resaltan en diferentes colores:



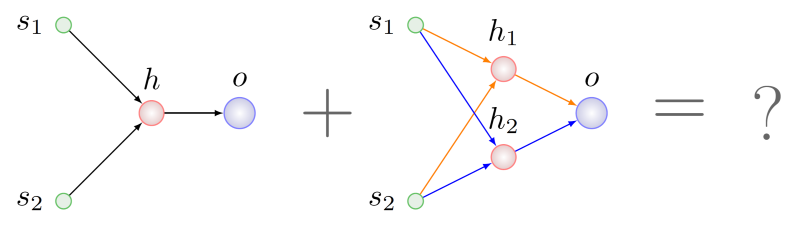
¿Cuál elegir para la recombinación con los genes parentales izquierdos?

Pasemos a la historia de la aparición de estos genotipos:



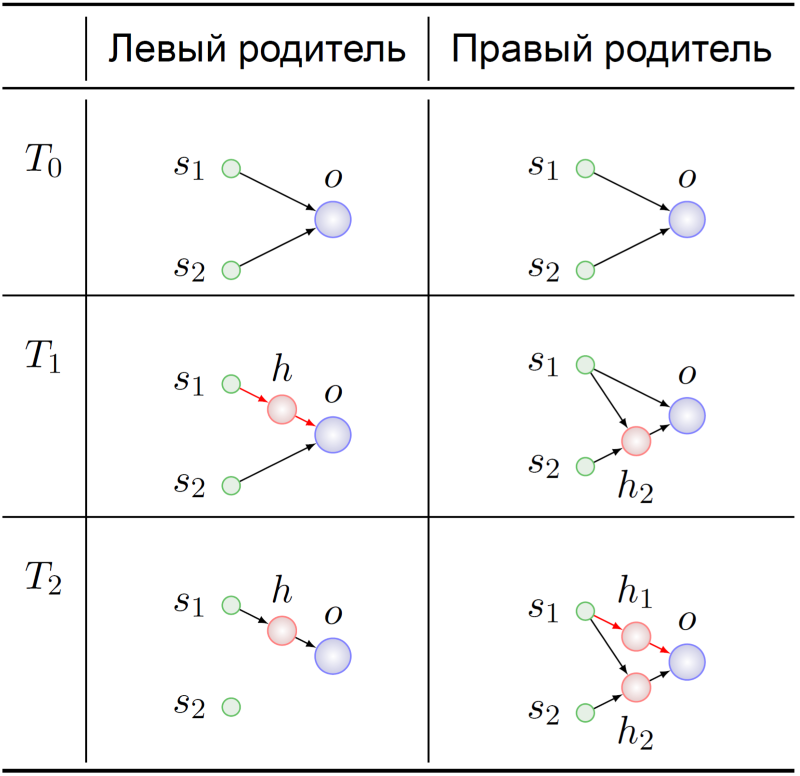
Ambos antepasados ​​de los agentes principales comenzaron, como se esperaba, con un mínimo de NS (T ₀ ). Sus genomas de alguna manera mutaron allí, y en el momento T ₁ , la neurona oculta se insertó en la conexión s ₁ -> o en el ancestro del progenitor izquierdo. En este momento dramático, los genes que codifican los enlaces s ₁ -> h y h -> o encuentran su significado en el antepasado del progenitor izquierdo: sustitución del enlace s ₁ -> o .
Los genes s ₁ -> h ₁ y h ₁ -> o en el genotipo del progenitor derecho en el momento T ₂ tienen exactamente el mismo significado. El futuro de nuestros antepasados ​​no es de particular interés para nosotros, ya sabemos con qué mezclarnos:



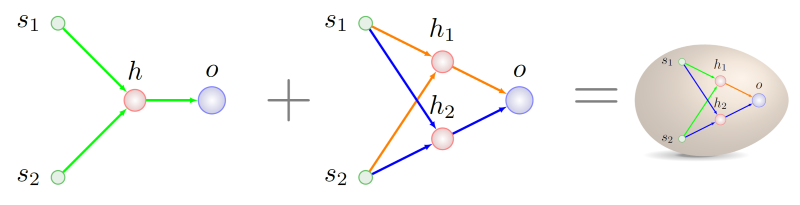
Cómo escribir la historia genética correctamente, será posible distinguir la próxima vez, especialmente dado que tenemos algunos pequeños hallazgos en esta área, están asociados con la adaptación de la técnica original a un esquema de reproducción estable.

Es hora de redondear. El artículo comenzó con Youtube, y lo completaremos. En una versión anterior del simulador, un colega que escribió el código para generar la pista lo terminó sin nada, un abismo sin fondo. La reacción de una red neuronal que ha evolucionado durante mucho tiempo en presencia de un firmamento terrestre bajo ruedas a un diseño de este pequeño universo tal vez se pueda llamar un "quiebre de plantilla":


Se puede encontrar una extensa colección de otras historias anecdóticas de la vida de los cibernaturalistas en [3] .

Fuentes

[1] KO Stanley y R .. Miikkulainen, Evolución de las redes neuronales a través del aumento de topologías Computación evolutiva, vol. 10, no. 2, pp. 99-127, 2002.
[2] C. Green, "Una revisión de las funciones de activación en SharpNEAT", 19 de junio de 2017.
[3] J. Lehman et al, "La creatividad sorprendente de la evolución digital: una colección de anécdotas de las comunidades de investigación evolutiva de computación y vida artificial", arXiv: Neural and Evolutionary Computing, 2018.