Desenfoque de Laplace: ¿es posible borrar Laplace en lugar de Gauss, cuántas veces es más rápido y vale la pena perder 1/32 de precisión?

"Desenfoque" en la gente común es un efecto de desenfoque en el procesamiento de imágenes digitales. Puede ser muy eficaz en sí mismo y como componente de animaciones de interfaz o efectos derivados más complejos (bloom / focusBlur / motionBlur). Con todo esto, los azules honestos en la frente son bastante lentos. Y a menudo las implementaciones integradas en la plataforma de destino dejan mucho que desear. O la velocidad es triste, los artefactos lastiman los ojos. La situación da lugar a muchas implementaciones de compromiso que son mejores o peores para ciertas condiciones. Una implementación original con buena calidad de confiabilidad y la velocidad más alta, mientras que la dependencia más baja del hardware lo está esperando. Buen provecho!

(Desenfoque de Laplace - Nombre del algoritmo original propuesto)

Hoy, mi demoscene interno me dio una patada y me obligó a escribir un artículo que tenía que ser escrito hace seis meses. Como aficionado, durante el tiempo libre, para desarrollar algoritmos de efectos originales, me gustaría ofrecer al público un algoritmo de "casi blurah gausiano", caracterizado por el uso de instrucciones de procesador excepcionalmente rápidas (cambios y máscaras), y por lo tanto accesible para la implementación hasta microcontroladores (extremadamente rápido en un entorno limitado).

De acuerdo con mi tradición de escribir artículos sobre Habr, daré ejemplos en JS como el lenguaje más popular, y lo creas o no, es muy conveniente para la creación rápida de prototipos de algoritmos. Además, la capacidad de implementar esto de manera efectiva en JS vino con matrices escritas. En mi portátil no muy potente, la imagen de pantalla completa se procesa a una velocidad de 30 fps (no se incluyó el subprocesamiento múltiple de los trabajadores).


Esta descripción está presente aquí más bien para explicar el curso de mis pensamientos y conjeturas que me llevaron al resultado. Para quienes estén interesados:

Función original de Gauss:



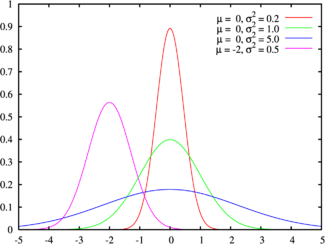
g (x) = a * e ** (- ((xb) ** 2) / c), donde
a es la amplitud (si tenemos ocho bits de color por canal, entonces = 256)
e es la constante de Euler ~ 2.7
b - cambio de gráfico en x (no necesitamos = 0)
c - parámetro que afecta el ancho del gráfico asociado con él como ~ w / 2.35

Nuestra función privada (menos del exponente eliminado con el reemplazo de la multiplicación por división):



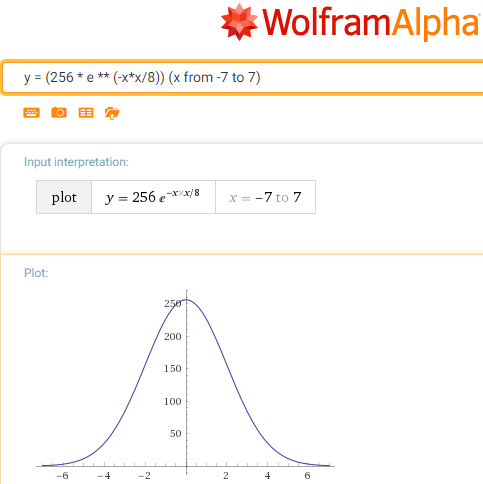
g (x) = 256 / e ** (x * x / c)

Que comience la acción de aproximación sucia:
Tenga en cuenta que el parámetro c está muy cerca de la mitad del ancho y establece 8 (esto se debe a cuántos pasos puede cambiar un canal de 8 bits cada uno).

También reemplazamos aproximadamente e por 2, sin embargo, notando que esto afecta la curvatura de la "campana" más que sus bordes. En realidad, afecta 2 / e veces, pero la sorpresa es que este error compensa el parámetro c, de modo que las condiciones de contorno todavía están en orden, y el error aparece solo en una "distribución normal" ligeramente incorrecta, para el gráfico algoritmos, esto afectará la dinámica de las transiciones de color de gradiente, pero es casi imposible notarlo a simple vista.

Entonces ahora nuestra función es la siguiente:
gg (x) = 256/2 ** (x * x / 8) o gg (x) = 2 ** (8 - x * x / 8)
Tenga en cuenta que el exponente (x * x / 8) tiene el mismo rango de valores [0-8] que la función de un orden inferior abs (x), por lo tanto, este último es un candidato para el reemplazo. Comprobaremos rápidamente la suposición observando cómo cambia el gráfico con ella gg (x) = 256 / (2 ** abs (x)):

GaussBlur vs LaplasBlur:



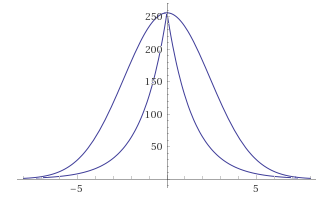
Las desviaciones parecen ser demasiado grandes, además, la función, habiendo perdido su suavidad, ahora tiene un pico. Pero oye.

Primero, no olvidemos que la suavidad de los gradientes obtenidos al difuminar no depende de la función de densidad de probabilidad (que es la función de Gauss), sino de su integral: la función de distribución. En ese momento, no conocía este hecho, pero de hecho, después de haber llevado a cabo una aproximación "destructiva" con respecto a la función de densidad de probabilidad (Gauss), la función de distribución se mantuvo bastante similar.

Fue:



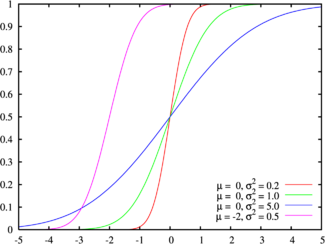
Se convirtió en:



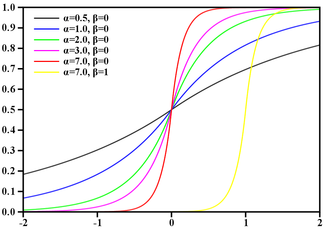
La prueba, tomada del algoritmo listo para usar, coincide:



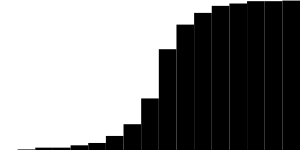
(Mirando hacia el futuro, diré que el error de desenfoque de mi algoritmo en relación con Gausian x5 fue solo del 3%).

Entonces, nos hemos acercado mucho más a la función de distribución de Laplace. Quién lo hubiera pensado, pero pueden lavar las imágenes un 97% no peor.

Prueba, diferencias Gausian blura x5 y "Laplace blura" x7:



(¡esto no es una imagen negra! Puedes estudiar en el editor)

La suposición de esta transformación nos permitió pasar a la idea de obtener el valor mediante filtrado iterativo, a lo que planeé reducir inicialmente.

Antes de decir un algoritmo específico, será honesto si corro hacia adelante e inmediatamente describo su único inconveniente (aunque la implementación se puede solucionar con una pérdida de velocidad). Pero este algoritmo se implementa usando aritmética de corte, y las potencias de 2 son su limitación. Por lo tanto, el original está hecho para difuminar x7 (que en las pruebas es más cercano a Gausian x5). Esta limitación de implementación se debe al hecho de que con un color de ocho bits, cambiando el valor en la unidad de filtro en un bit por paso, cualquier acción desde el punto finaliza en un máximo de 8 pasos. También implementé una versión un poco más lenta a través de proporciones y adiciones adicionales, que implementa una división rápida por 1.5 (resultando en un radio de x15). Pero con la aplicación adicional de este enfoque, el error aumenta y la velocidad disminuye, lo que no permite que se use así. Por otro lado, vale la pena señalar que x15 ya es suficiente para no notar la diferencia, el resultado se obtiene del original o de la imagen muestreada hacia abajo. Por lo tanto, el método es bastante adecuado si necesita una velocidad extraordinaria en un entorno limitado.

Entonces, el núcleo del algoritmo es simple, se realizan cuatro pases del mismo tipo:

1. La mitad del valor de la unidad t (inicialmente igual a cero) se agrega a la mitad del valor del siguiente píxel, el resultado se le asigna. Continúe de esta manera hasta el final de la línea de la imagen. Para todas las lineas.

Al completar la primera pasada, la imagen se ve borrosa en una dirección.

2. En la segunda pasada, hacemos lo mismo en la dirección opuesta para todas las líneas.
Obtenemos una imagen que está completamente borrosa horizontalmente.

3-4. Ahora haz lo mismo verticalmente.
Hecho

Inicialmente, utilicé un algoritmo de dos pasadas con la implementación de back-blur a través de la pila, pero es difícil de entender, no es elegante, y resultó ser más lento en las arquitecturas actuales. Quizás el algoritmo de una pasada sea más rápido en los microcontroladores, y la capacidad de generar el resultado progresivamente también será una ventaja.

El método actual de implementación de cuatro vías, miré a Habré del gurú anterior sobre algoritmos de desenfoque. habr.com/post/151157 Aprovecho esta oportunidad para expresarle mi solidaridad y mi profunda gratitud.

Pero los hacks no terminaron allí. ¡Ahora sobre cómo calcular los tres canales de color en una instrucción de procesador! El hecho es que el desplazamiento de bits utilizado como división entre dos le permite controlar muy bien la posición de los bits de resultado. El único problema es que los bits más bajos de los canales se deslizan hacia los canales vecinos más altos, pero simplemente puede restablecerlos, que solucionar el problema, con cierta pérdida de precisión. Y de acuerdo con la fórmula de filtro descrita, la adición de la mitad del valor de la unidad con la mitad del valor de la siguiente celda (sujeto a restablecer los bits descargados) nunca conduce al desbordamiento, por lo que no debe preocuparse por eso. Y la fórmula del filtro para el cálculo simultáneo de todos los dígitos se convierte en esto:

buf32 [i] = t = (((t >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

Sin embargo, se requiere una adición más: se descubrió experimentalmente que la pérdida de precisión en esta fórmula es demasiado significativa, el brillo de la imagen salta visualmente significativamente. Quedó claro que el bit perdido debe redondearse al entero más cercano y no descartarse. Una manera fácil de hacer esto en aritmética de enteros es agregar la mitad del divisor antes de la división. Nuestro divisor es dos, por lo que debe agregar uno, en todos los dígitos, la constante 0x010101. Pero con cualquier adición, uno debe tener cuidado con el desbordamiento. Por lo tanto, no podemos usar dicha corrección para calcular la mitad del valor de la siguiente celda. (Si hay color blanco, obtendremos un desbordamiento, por lo tanto, no lo corregiremos). Pero resultó que el error principal fue cometido por la división múltiple de la unidad, que podemos corregir. Porque, de hecho, incluso con tal corrección, el valor en la unidad no aumentará por encima de 254. Pero cuando se agrega a 0x010101, no se garantizará el desbordamiento. Y la fórmula del filtro con corrección toma la forma:

buf32 [i] = t = (((((0x010101 + t) >> 1) & 0x7F7F7F) + ((buf32 [i] >> 1) & 0x7F7F7F);

De hecho, la fórmula realiza la corrección bastante bien, por lo que cuando aplica repetidamente este algoritmo a la imagen, los artefactos comienzan a ser visibles solo en los segundos diez pases. (no el hecho de que repetir la blura gausiana no producirá tales artefactos).

Además, hay una propiedad maravillosa con muchos pases. (Esto no se debe a mi algoritmo, sino a la "normalidad" de la distribución normal). Ya en el segundo paso de Laplace Blura, la función de densidad de probabilidad (si supuse que todo está bien) se verá así:



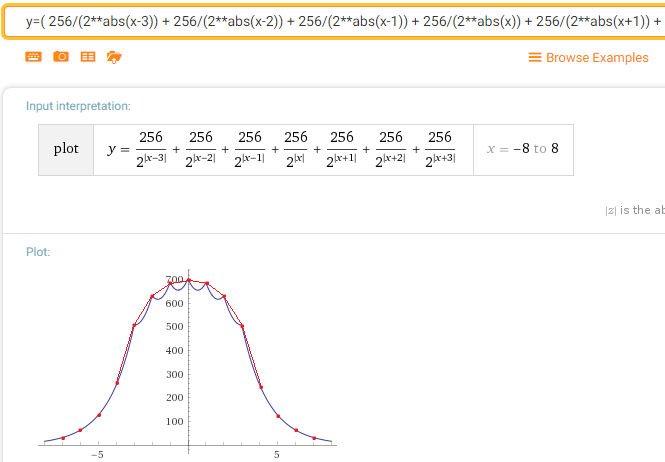
Lo cual, ya ves, ya está muy cerca del gaussiano.

Empíricamente, descubrí que usar modificaciones con un radio grande es permisible en pares, porque la propiedad descrita anteriormente compensa los errores si la última pasada es más precisa (la más precisa es el algoritmo de desenfoque x7 descrito aquí).

demo
rap
codpen

Un atractivo para los matemáticos geniales:
Lo que sería interesante saber qué tan correcto es usar dicho filtro por separado, no estoy seguro de si hay una imagen de distribución simétrica. Aunque la heterogeneidad del ojo no es visible.

upd: Aquí subiré enlaces útiles, amablemente presentados por comentaristas, y encontrados de otros Khabrovites.
1. Cómo funcionan los asistentes de inteligencia basados ​​en el poder de SSE - software.intel.com/en-us/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (gracias vladimirovich )
2. Base teórica sobre el tema "Convoluciones de imagen rápidas" + algunas de sus aplicaciones personalizadas en relación con el honesto gaussiano azul - blog.ivank.net/fastest-gaussian-blur.html (gracias Grox )

Sugerencias, comentarios, críticas constructivas son bienvenidas!