Verificación numérica de la hipótesis abc (sí, esa)

Hola Habr

Ya se han publicado varios artículos sobre la hipótesis abc en el Geektimes Habr (por ejemplo, en 2013 y 2018 ). La historia en sí misma sobre un teorema que al principio no se puede probar durante muchos años, y luego no se puede verificar durante el mismo número de años, ciertamente merece al menos una película. Pero a la sombra de esta maravillosa historia, el teorema en sí mismo se considera demasiado superficialmente, aunque no es menos interesante. Ya al ​​menos por el hecho de que la hipótesis ABC es uno de los pocos problemas no resueltos de la ciencia moderna, la declaración del problema que incluso un alumno de quinto grado puede entender. Si esta hipótesis es realmente cierta, entonces fácilmente sigue la prueba de otros teoremas importantes, por ejemplo, la prueba del teorema de Fermat .

Sin reclamar los laureles de Motizuki, también decidí tratar de comprobar con una computadora cuánto se cumple la igualdad prometida en la hipótesis. En realidad, ¿por qué no? Los procesadores modernos no son solo para jugar, sino por qué no usar una computadora para su propósito principal (computación) ...

A quién le importa lo que pasó, por favor, debajo del gato.

Declaración del problema.

Comencemos desde el principio. ¿De qué trata el teorema? Como dice Wikipedia (la redacción en la versión en inglés es un poco más clara), para números primos mutuamente (que no tienen divisores comunes) a, byc de modo que a + b = c, para cualquier ε> 0 hay un número limitado de triples a + b = c, de modo que:



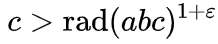
La función rad se llama radical y denota el producto de factores primos de un número. Por ejemplo, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 es un número primo), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1,000,000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.

En realidad, la esencia del teorema es que el número de triples es bastante pequeño. Por ejemplo, si tomamos al azar ε = 0.2 y la igualdad 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1.2 es claramente mayor que 127, la desigualdad no se cumple. Pero hay excepciones, por ejemplo, para la igualdad 49 + 576 = 625, se cumple la condición del teorema (aquellos que lo deseen pueden verificar por sí mismos).

El siguiente momento clave para nosotros es un número limitado de estas igualdades, según el teorema. Es decir Esto significa que simplemente puede intentar ordenarlos en una computadora. Como resultado, esto nos da al Premio Nobel una tarea de programación bastante interesante.

Entonces comencemos.

Código fuente

La primera versión fue escrita en Python, y aunque este lenguaje es demasiado lento para tales cálculos, escribir código en él es fácil y simple, lo cual es conveniente para la creación de prototipos.

Obteniendo el radical : descomponemos el número en factores primos, luego eliminamos las repeticiones, convirtiendo la matriz en un conjunto. Luego solo obtenga el producto de todos los elementos.

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

Números primos mutuos : factoriza los números y simplemente verifica la intersección de los conjuntos.

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

Verificación : utilizamos funciones ya creadas, todo es simple aquí.

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

Aquellos que lo deseen pueden experimentar de forma independiente copiando el código anterior en cualquier editor de lenguaje Python en línea. Por supuesto, el código se ejecuta como se esperaba y enumerar todos los triples a al menos un millón sería demasiado largo. Debajo del spoiler hay una versión optimizada, se recomienda usarlo.

La versión final se reescribió en C ++ utilizando subprocesos múltiples y cierta optimización (trabajar en C con conjuntos de intersección sería demasiado duro, aunque probablemente más rápido). El código fuente está debajo del spoiler, se puede compilar en el compilador g ++ gratuito, el código funciona en Windows, OSX e incluso en Raspberry Pi.


Para aquellos que son demasiado flojos para instalar el compilador de C ++, se proporciona una versión de Python ligeramente optimizada, que se puede ejecutar en cualquier editor en línea (utilicé https://repl.it/languages/python ).

Resultados

Los triples a, b, c son realmente muy pocos.

Algunos resultados se dan a continuación:
N = 10 : 1 "tres", tiempo de entrega <0.001c
1 + 8 = 9

N = 100 : 2 "triples", tiempo de ejecución <0.001c
1 + 8 = 9
1 + 80 = 81

N = 1000 : 8 "triples", tiempo de ejecución <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

N = 10000 : 23 "triples", tiempo de ejecución 2s


N = 100000 : 53 triples, tiempo de ejecución 50c


Con N = 1,000,000, tenemos solo 102 "triples", una lista completa se da debajo del spoiler.


Por desgracia, el programa aún funciona lentamente, no esperé los resultados para N = 10,000,000, el tiempo de cálculo es más de una hora (tal vez cometí un error al optimizar el algoritmo en algún lugar, y puedo hacerlo mejor).

Es aún más interesante ver los resultados gráficamente:



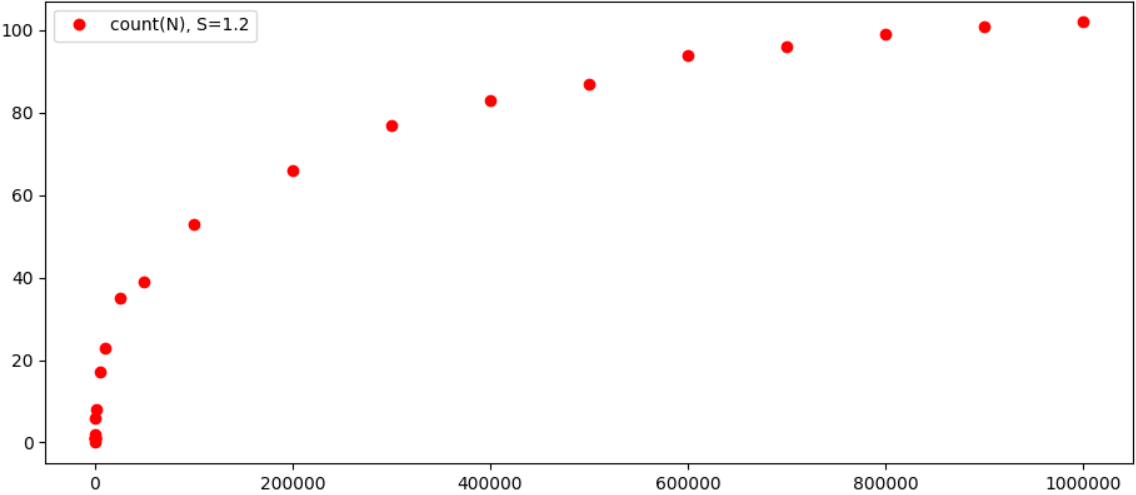
En principio, es bastante obvio que la dependencia del número de triples posibles en N crece notablemente más lento que N en sí mismo, y es probable que el resultado converja en algún número específico para cada ε. Por cierto, con un aumento en ε, el número de triples disminuye notablemente, por ejemplo, para ε = 0.4 tenemos solo 2 igualdades para N <100000 (1 + 4374 = 4375 y 343 + 59049 = 59392). Entonces, en general, parece que el teorema realmente se cumple (bueno, y probablemente ya se haya probado en computadoras más potentes, y tal vez todo esto se haya calculado durante mucho tiempo).

Aquellos que lo deseen pueden experimentar por su cuenta, si alguien tiene resultados para números 10,000,000 y superiores, estaré encantado de agregarlos al artículo. Por supuesto, sería interesante "contar" hasta el momento en que el conjunto de "triples" deje de crecer por completo, pero puede llevar mucho tiempo, la velocidad de cálculo parece depender de N como N * N (o tal vez N ^ 3), y el proceso muy largo Sin embargo, hay algo sorprendente cerca, y aquellos que lo deseen pueden unirse a la búsqueda.

Editar: como se sugiere en los comentarios, Wikipedia ya tiene una tabla con los resultados : en el rango N hasta 10 ^ 18 el número de "triples" sigue creciendo, por lo que aún no se ha encontrado el "final" del conjunto. Aún más interesante: la intriga aún permanece.