Más recientemente, tuve que resolver otra tarea trivial de capacitación de mi maestro. Sin embargo, al resolverlo, logré llamar la atención sobre cosas en las que no había pensado antes, y es posible que tampoco lo hayas pensado. Es más probable que este artículo sea útil para los estudiantes y para todos los que comienzan su viaje al mundo de la programación paralela utilizando MPI.

Nuestro "Dado:"
Entonces, la esencia de nuestra tarea esencialmente computacional es comparar cuántas veces un programa que usa transferencias punto a punto retardadas sin bloqueo es más rápido que el que usa transferencias punto a punto de bloqueo. Realizaremos mediciones para matrices de entrada de 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 elementos. Por defecto, se propone resolverlo mediante cuatro procesos. Y aquí, de hecho, es lo que consideraremos:
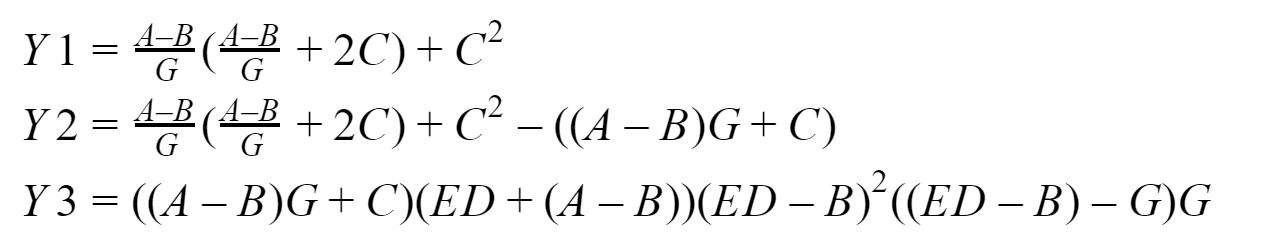
En la salida, deberíamos obtener tres vectores: Y1, Y2 e Y3, que el proceso cero recopilará. Probaré todo esto en mi sistema basado en
un procesador Intel con 16 GB de RAM. Para desarrollar programas, utilizaremos la implementación del estándar
MPI de Microsoft versión 9.0.1 (en el momento de la redacción, es relevante), Visual Studio Community 2017 y no Fortran.
Materiel
No me gustaría describir en detalle cómo funcionan las funciones MPI que se utilizarán, siempre puede ir a
ver la documentación para esto , por lo que solo daré una breve descripción de lo que usaremos.
Bloqueo de intercambio
Para bloquear la mensajería punto a punto, utilizaremos las funciones:MPI_Send : implementa el envío de mensajes de bloqueo, es decir después de llamar a la función, el proceso se bloquea hasta que los datos que se le envían se escriben desde su memoria en el búfer interno del sistema MPI, después de lo cual el proceso continúa trabajando más;
MPI_Recv : realiza la recepción de mensajes de bloqueo, es decir Después de llamar a la función, el proceso se bloquea hasta que lleguen los datos del proceso de envío y hasta que el entorno MPI escriba completamente estos datos en el búfer del proceso de recepción.
Intercambio diferido sin bloqueo
Para mensajes diferidos de punto a punto sin bloqueo, utilizaremos las funciones:MPI_Send_init : en segundo plano, prepara el entorno para enviar datos que sucederán en el futuro y sin bloqueos;
MPI_Recv_init : esta función funciona de manera similar a la anterior, solo que esta vez para recibir datos;
MPI_Start : inicia el proceso de recibir o transmitir un mensaje, también se ejecuta en segundo plano a.k.a. sin bloqueo
MPI_Wait : se utiliza para verificar y, si es necesario, esperar a que finalice el envío o la recepción de un mensaje, pero simplemente bloquea el proceso si es necesario (si los datos no se "envían" o "no se reciben"). Por ejemplo, un proceso quiere usar datos que aún no lo hayan alcanzado; no es bueno, por lo tanto, insertamos MPI_Wait delante del lugar donde necesitará estos datos (los insertamos incluso si simplemente existe el riesgo de corrupción de datos). Otro ejemplo, el proceso comenzó la transferencia de datos en segundo plano, y después de comenzar la transferencia de datos, inmediatamente comenzó a cambiar estos datos de alguna manera, no es bueno, por lo que insertamos MPI_Wait delante del lugar en el programa donde comienza a cambiar estos datos (aquí también los insertamos incluso si simplemente existe el riesgo de corrupción de datos).
Por lo tanto,
semánticamente la secuencia de llamadas con un intercambio diferido sin bloqueo es la siguiente:
- MPI_Send_init / MPI_Recv_init: preparación del entorno para recibir o transmitir
- MPI_Start - comienza el proceso de recepción / transmisión
- MPI_Wait: llamamos a riesgo de daños (incluyendo "comprensión" y "recepción insuficiente") de datos transmitidos o recibidos
También utilicé
MPI_Startall ,
MPI_Waitall en mis programas de prueba, su significado es básicamente el mismo que MPI_Start y MPI_Wait, respectivamente, solo que operan en varios paquetes y / o transmisiones. Pero esta no es la lista completa de las funciones de inicio y espera, hay varias funciones más para verificar la integridad de las operaciones.
Arquitectura entre procesos
Para mayor claridad, construimos un gráfico para realizar cálculos mediante cuatro procesos. En este caso, uno debería tratar de distribuir todas las operaciones aritméticas vectoriales de manera relativamente uniforme sobre los procesos. Esto es lo que obtuve:
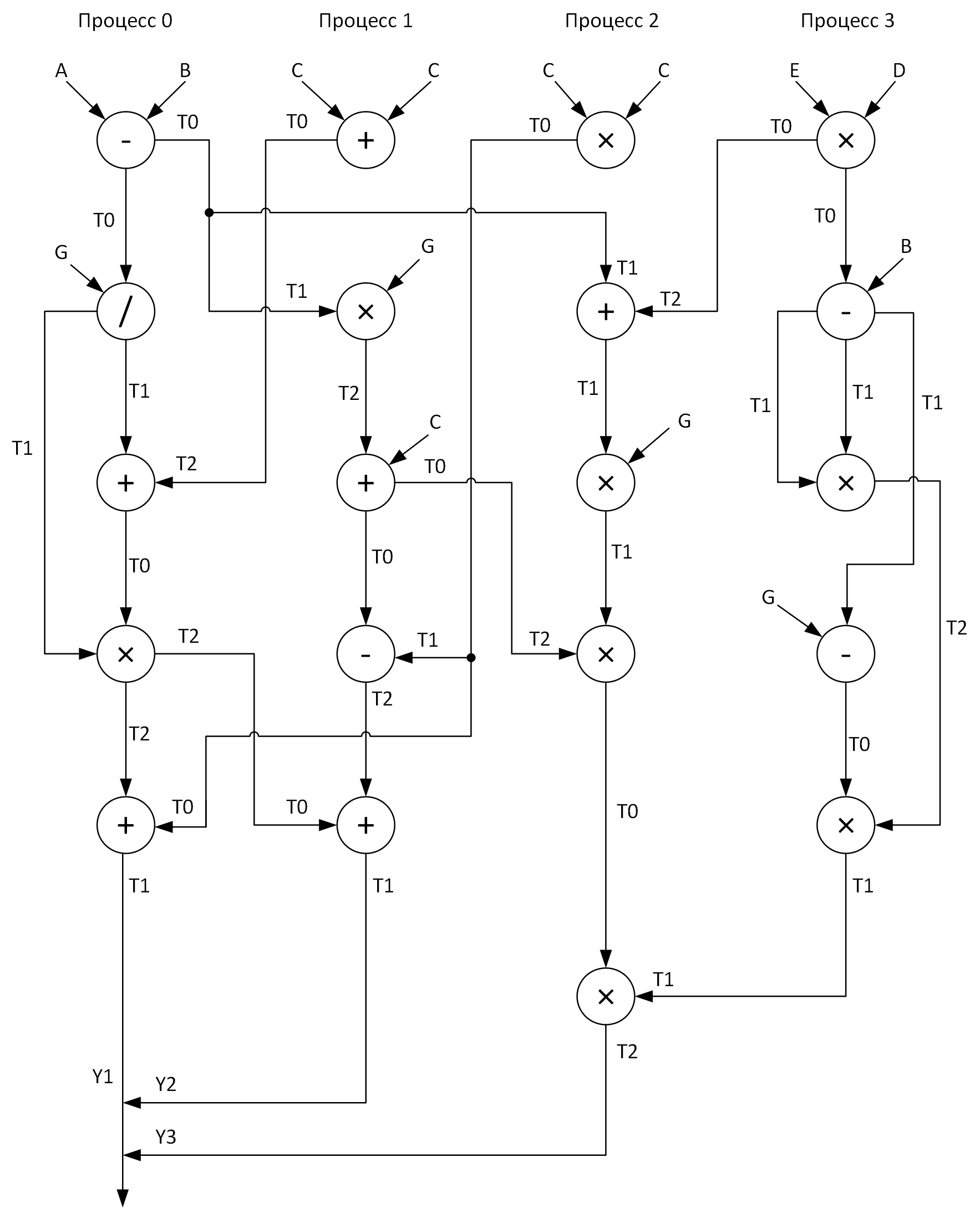
Ver estos arreglos T0-T2? Estos son buffers para almacenar resultados intermedios de operaciones. Además, en un gráfico al enviar mensajes de un proceso a otro, al comienzo de la flecha se encuentra el nombre de la matriz cuyos datos se transmiten, y al final de la flecha se encuentra la matriz que recibe estos datos.
Bueno, cuando finalmente respondimos las preguntas:
- ¿Qué tipo de problema estamos resolviendo?
- ¿Qué herramientas usaremos para resolverlo?
- ¿Cómo lo resolveremos?
Solo queda resolverlo ...
Nuestra "solución"
A continuación, presentaré los códigos de los dos programas discutidos anteriormente, pero para empezar, daré algunas explicaciones más de qué y cómo.
Saqué todas las operaciones aritméticas de vectores en procedimientos separados (add, sub, mul, div) para aumentar la legibilidad del código. Todas las matrices de entrada se inicializan de acuerdo con las fórmulas que indiqué
casi al azar. Dado que el proceso cero recopila los resultados del trabajo de todos los demás procesos, por lo tanto, funciona más tiempo, por lo tanto, es lógico considerar el tiempo de su trabajo igual al tiempo de ejecución del programa (como recordamos, estamos interesados en: aritmética + mensajería) en el primer y segundo casos.
Mediremos los intervalos de tiempo usando la función
MPI_Wtime, y al mismo tiempo decidí mostrar qué resolución de los relojes tengo allí usando
MPI_Wtick (en algún lugar de mi alma espero que encajen en mi TSC invariante, en este caso, incluso estoy listo para perdonarles el error asociado con el momento en que la función se llamaba MPI_Wtime). Entonces, reuniremos todo lo que escribí anteriormente y de acuerdo con el gráfico finalmente desarrollaremos estos programas (y depuración, por supuesto).
A quién le importa ver el código:
Programa con bloqueo de transferencias de datos#include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Status status; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double (2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); sub(A, B, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); div(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); add(T0, T2, T1, n); MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { add(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); mul(T1, G, T2, n); add(T2, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T1, T0, T2, n); MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); add(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 2) { mul(C, C, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status); MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD); MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); add(T1, T2, T0, n); mul(T0, G, T1, n); MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status); mul(T1, T2, T0, n); MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status); mul(T0, T1, T2, n); MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD); } if (rank == 3) { mul(E, D, T0, n); MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); sub(T0, B, T1, n); mul(T1, T1, T2, n); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Programa con transferencias de datos no bloqueadas diferidas #include "pch.h" #include <iostream> #include <iomanip> #include <fstream> #include <mpi.h> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main(int argc, char **argv) { if (argc < 2) { return 1; } int n = atoi(argv[1]); int rank; double start_time, end_time; MPI_Request request[7]; MPI_Status statuses[4]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; double *D = new double[n]; double *E = new double[n]; double *G = new double[n]; double *T0 = new double[n]; double *T1 = new double[n]; double *T2 = new double[n]; for (int i = 0; i < n; i++) { A[i] = double(2 * i + 1); B[i] = double(2 * i); C[i] = double(0.003 * (i + 1)); D[i] = A[i] * 0.001; E[i] = B[i]; G[i] = C[i]; } cout.setf(ios::fixed); cout << fixed << setprecision(9); MPI_Init(&argc, &argv); MPI_Comm_rank(MPI_COMM_WORLD, &rank); if (rank == 0) { start_time = MPI_Wtime(); MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);// MPI_Start(&request[2]); sub(A, B, T0, n); MPI_Startall(2, &request[0]); div(T0, G, T1, n); MPI_Waitall(3, &request[0], statuses); add(T1, T2, T0, n); mul(T0, T1, T2, n); MPI_Startall(2, &request[3]); MPI_Wait(&request[3], &statuses[0]); add(T0, T2, T1, n); MPI_Startall(2, &request[5]); MPI_Wait(&request[4], &statuses[0]); MPI_Waitall(2, &request[5], statuses); end_time = MPI_Wtime(); cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl; cout << "Thread " << rank << " execution time: " << end_time - start_time << endl; } if (rank == 1) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);// MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);// MPI_Start(&request[0]); add(C, C, T0, n); MPI_Start(&request[1]); MPI_Wait(&request[0], &statuses[0]); mul(T1, G, T2, n); MPI_Start(&request[2]); MPI_Wait(&request[1], &statuses[0]); add(T2, C, T0, n); MPI_Start(&request[3]); MPI_Wait(&request[2], &statuses[0]); sub(T1, T0, T2, n); MPI_Wait(&request[3], &statuses[0]); MPI_Start(&request[4]); MPI_Wait(&request[4], &statuses[0]); add(T0, T2, T1, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); } if (rank == 2) { MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);// MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);// MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);// MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);// MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);// MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);// MPI_Startall(2, &request[0]); mul(C, C, T0, n); MPI_Startall(2, &request[2]); MPI_Waitall(4, &request[0], statuses); add(T1, T2, T0, n); MPI_Start(&request[4]); mul(T0, G, T1, n); MPI_Wait(&request[4], &statuses[0]); mul(T1, T2, T0, n); MPI_Start(&request[5]); MPI_Wait(&request[5], &statuses[0]); mul(T0, T1, T2, n); MPI_Start(&request[6]); MPI_Wait(&request[6], &statuses[0]); } if (rank == 3) { MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]); MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]); mul(E, D, T0, n); MPI_Start(&request[0]); sub(T0, B, T1, n); mul(T1, T1, T2, n); MPI_Wait(&request[0], &statuses[0]); sub(T1, G, T0, n); mul(T0, T2, T1, n); MPI_Start(&request[1]); MPI_Wait(&request[1], &statuses[0]); } MPI_Finalize(); delete[] A; delete[] B; delete[] C; delete[] D; delete[] E; delete[] G; delete[] T0; delete[] T1; delete[] T2; return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Pruebas y análisis.
Ejecutemos nuestros programas para matrices de diferentes tamaños y veamos qué sucede. Los resultados de la prueba se resumen en la tabla, en la última columna de la cual calculamos y escribimos el coeficiente de aceleración, que definimos de la siguiente manera: K
accele = T
ex. sin bloque. / T
bloque.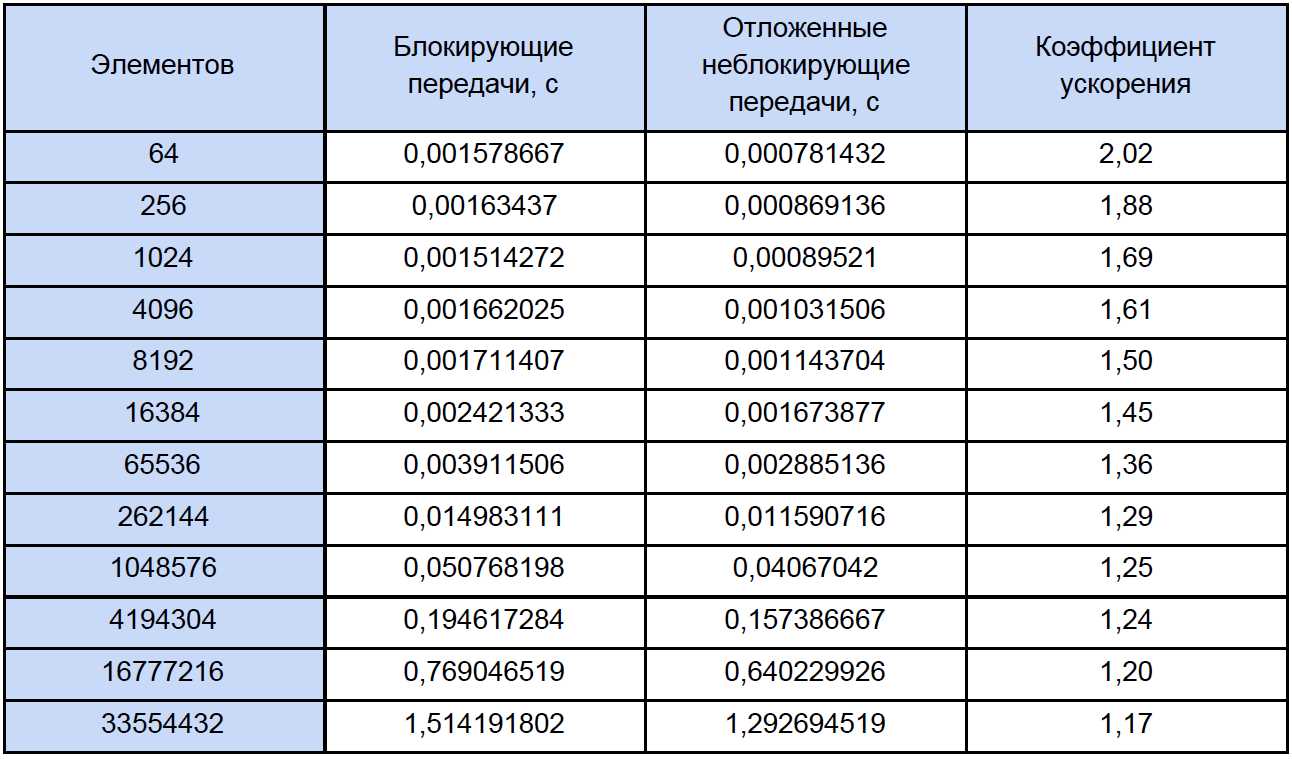
Si observa esta tabla con un poco más de cuidado de lo habitual, notará que con un aumento en el número de elementos procesados, el coeficiente de aceleración disminuye de alguna manera de esta manera:

¿Intentamos determinar cuál es el problema? Para hacer esto, propongo escribir un pequeño programa de prueba que mida el tiempo de cada operación aritmética vectorial y reduzca cuidadosamente los resultados a un archivo de texto ordinario.
Aquí, de hecho, el programa en sí:
Medida del tiempo #include "pch.h" #include <iostream> #include <iomanip> #include <Windows.h> #include <fstream> using namespace std; void add(double *A, double *B, double *C, int n); void sub(double *A, double *B, double *C, int n); void mul(double *A, double *B, double *C, int n); void div(double *A, double *B, double *C, int n); int main() { struct res { double add; double sub; double mul; double div; }; int i, j, k, n, loop; LARGE_INTEGER start_time, end_time, freq; ofstream fout("test_measuring.txt"); int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 }; SetConsoleOutputCP(1251); cout << " loop: "; cin >> loop; fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9); fout << " : " << loop << endl; fout << setw(10) << "\n " << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << setw(30) << ". (c)" << endl; QueryPerformanceFrequency(&freq); cout << "\n : " << freq.QuadPart << " " << endl; for (k = 0; k < sizeof(N) / sizeof(int); k++) { res output = {}; n = N[k]; double *A = new double[n]; double *B = new double[n]; double *C = new double[n]; for (i = 0; i < n; i++) { A[i] = 2.0 * i; B[i] = 2.0 * i + 1; C[i] = 0; } for (j = 0; j < loop; j++) { QueryPerformanceCounter(&start_time); add(A, B, C, n); QueryPerformanceCounter(&end_time); output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); sub(A, B, C, n); QueryPerformanceCounter(&end_time); output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); mul(A, B, C, n); QueryPerformanceCounter(&end_time); output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); QueryPerformanceCounter(&start_time); div(A, B, C, n); QueryPerformanceCounter(&end_time); output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart); } fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop << setw(30) << output.mul / loop << setw(30) << output.div / loop << endl; delete[] A; delete[] B; delete[] C; } fout.close(); cout << endl; system("pause"); return 0; } void add(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] + B[i]; } } void sub(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] - B[i]; } } void mul(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] * B[i]; } } void div(double *A, double *B, double *C, int n) { for (size_t i = 0; i < n; i++) { C[i] = A[i] / B[i]; } }
Al inicio, le pide que ingrese el número de ciclos de medición, probé durante 10,000 ciclos. En la salida, obtenemos el resultado promedio para cada operación:
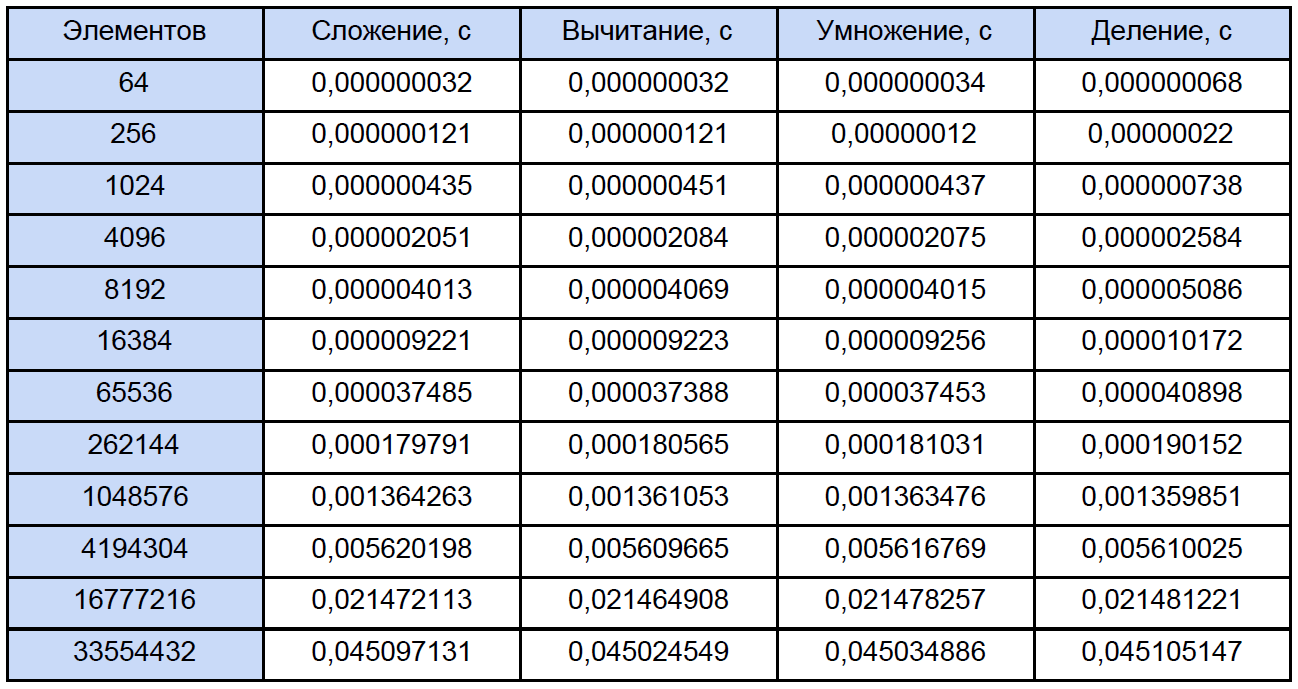
Para medir el tiempo, utilicé el
QueryPerformanceCounter de alto nivel. Recomiendo leer
estas preguntas frecuentes para que la mayoría de las preguntas sobre la medición del tiempo con esta función desaparezcan por sí mismas. Según mis observaciones, se aferra al TSC (pero en teoría puede que no sea por ello), pero devuelve, según la ayuda, el número actual de tics del contador. Pero el hecho es que mi contador físicamente no puede medir el intervalo de tiempo de 32 ns (vea la primera fila de la tabla de resultados). Este resultado se debe al hecho de que entre las dos llamadas del QueryPerformanceCounter pasan 0 ticks o 1 ticks. Para la primera fila de la tabla, solo podemos concluir que aproximadamente un tercio de los 10,000 resultados son 1 tick.
Entonces, los datos en esta tabla para 64, 256 e incluso para 1024 elementos son algo aproximados. Ahora, abramos cualquiera de los programas y calculemos cuántas operaciones totales de cada tipo encuentra, tradicionalmente "distribuiremos" todo según la siguiente tabla:
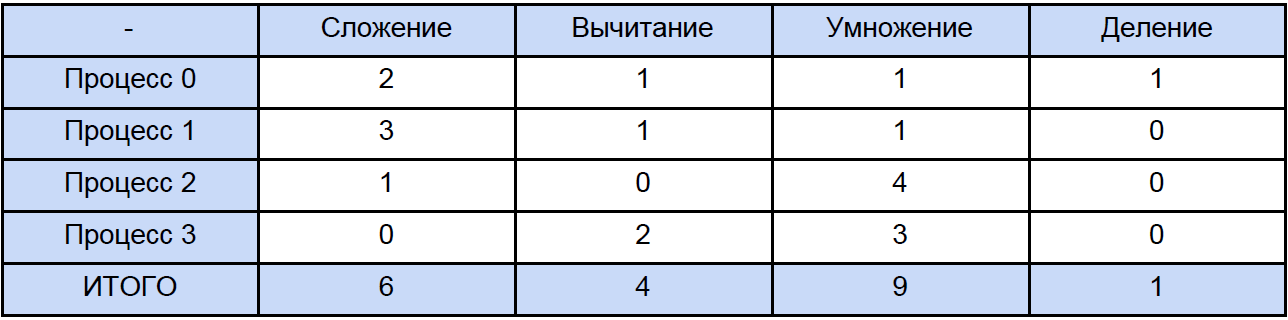
Finalmente, sabemos el tiempo de cada operación aritmética de vectores y cuánto es en nuestro programa, tratamos de averiguar cuánto tiempo se dedica a estas operaciones en programas paralelos y cuánto tiempo se dedica al bloqueo y al intercambio diferido de datos sin bloqueo entre procesos y nuevamente, para mayor claridad, reduciremos esto a tabla:
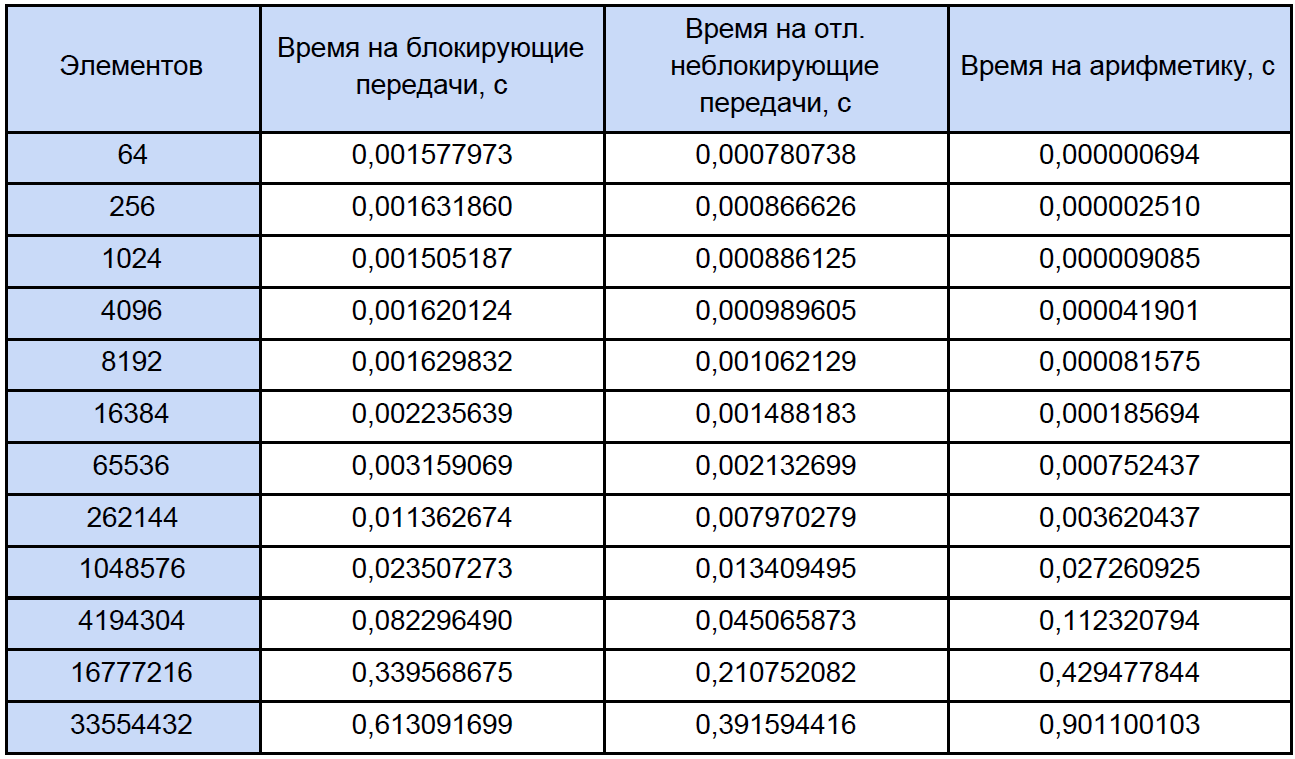
Con base en los resultados de los datos obtenidos, construimos un gráfico de tres funciones: la primera describe el cambio en el tiempo dedicado a bloquear transferencias entre procesos, a partir del número de elementos de la matriz, la segunda describe el cambio en el tiempo dedicado a transferencias diferidas sin bloqueo entre procesos, en la cantidad de elementos de la matriz y la tercera describe el cambio en el tiempo, gastado en operaciones aritméticas, a partir del número de elementos de las matrices:
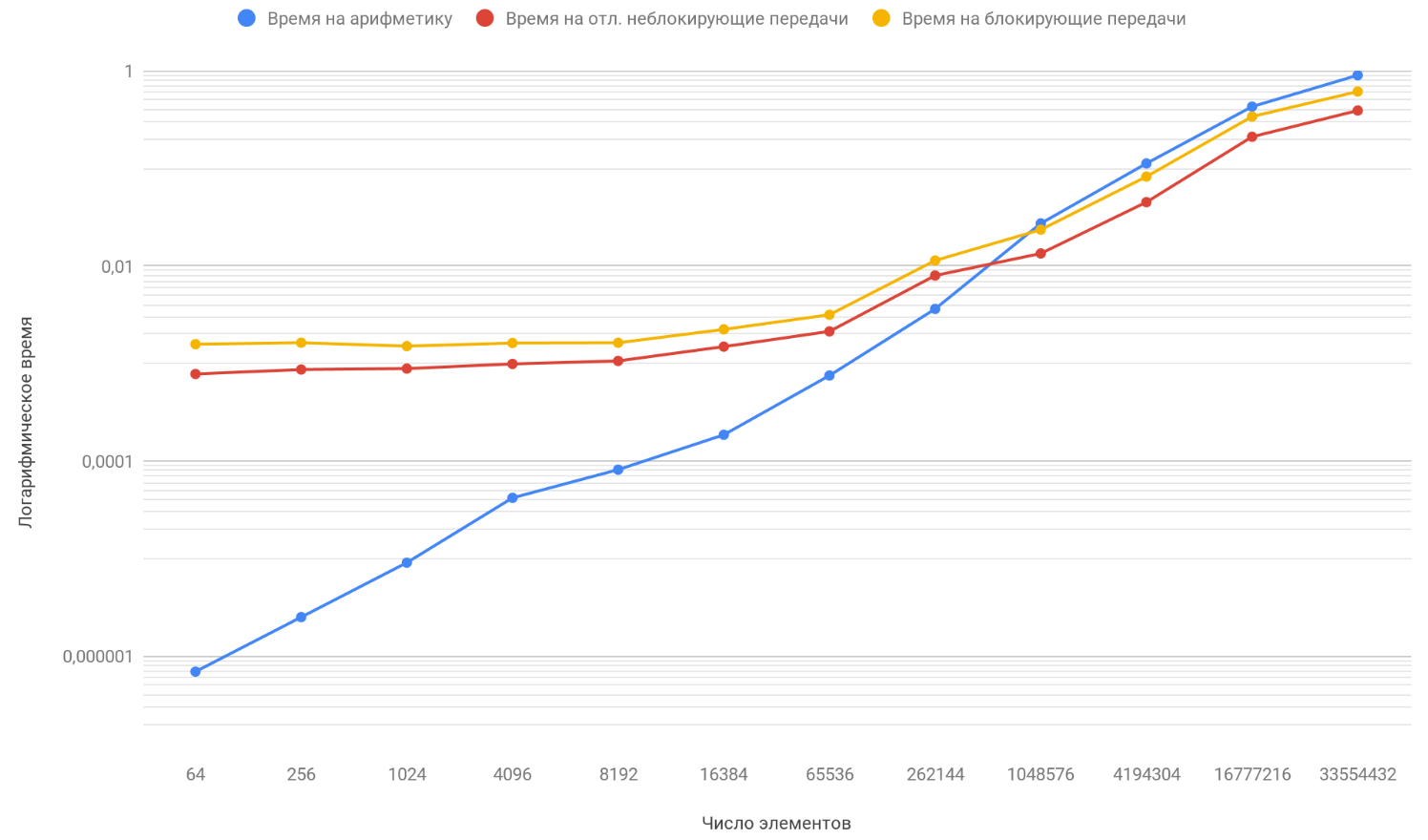
Como ya ha notado, la escala vertical del gráfico es logarítmica, es una medida necesaria, porque la dispersión de los tiempos es demasiado grande y, en un gráfico regular, nada habría sido visible. Preste atención a la función de la dependencia del tiempo dedicado a la aritmética en el número de elementos, ya que supera con seguridad las otras dos funciones en aproximadamente 1 millón de elementos. El caso es que crece al infinito más rápido que sus dos oponentes. Por lo tanto, con un aumento en el número de elementos procesados, el tiempo de ejecución de los programas está cada vez más determinado por la aritmética en lugar de las transferencias. Suponga que aumenta el número de transferencias entre procesos, conceptualmente solo verá que el momento en que la función aritmética supere a las otras dos sucederá más tarde.
Resumen
Por lo tanto, si continúa aumentando la longitud de las matrices, llegará a la conclusión de que un programa con transferencias diferidas sin bloqueo será solo un poco más rápido que el que usa el intercambio de bloqueo. Y si dirige la longitud de las matrices al infinito (bueno, o simplemente toma matrices muy largas), entonces el tiempo de funcionamiento de su programa estará determinado al 100% por los cálculos, y el coeficiente de aceleración tenderá a 1 de manera segura.