En marzo de 2016, Robert J. Lemke-Oliver y Kannan Sundararajan de la Universidad de Stanford
abrieron un nuevo patrón en la distribución de números primos. Resultó que los primos se distribuyen
específicamente en el espacio numérico. Para más detalles, vea la traducción del artículo
"Estructura y aleatoriedad de primos" en Habré.
Expertos de otros campos, incluida la química, se unieron al estudio del tema. Y con exito. El profesor de Química Teórica
Salvatore Torcuato, junto con el teórico de números
Matthew de Courcy-Irlanda, encontró
nuevos patrones en la distribución de los números primos que no se conocían previamente. Resultó que la distribución de los números primos forma un patrón de difracción de tipo fractal, algo similar al patrón de difracción de cuasicristales exóticos.
El profesor Torcuato se especializa en el estudio de patrones en las estructuras de sistemas físicos, como cristales y coloides. La forma estándar de estudiar la estructura es la difracción de rayos X. Las moléculas aleatorias en líquidos o gases reflejan los rayos en todas las direcciones sin crear un patrón notable. Pero los átomos ubicados simétricamente en el cristal reflejan sincrónicamente las ondas de luz, creando puntos brillantes periódicos de difracción pronunciada (
picos de Bragg ). Un análisis de los picos de Bragg permite comprender la estructura interna de un cristal u otro material que crea dicha imagen.
Entonces, en nuevos artículos científicos de Torkuato y otros (
1 ,
2 ,
3 ) se muestra que la estructura ordenada descubierta en la distribución de los números primos no es más que un patrón de difracción similar a un fractal, similar al de los cuasicristales.
La imagen de los picos de Bragg en una red de números primos es similar a los cuasicristales, pero aún difiere de ellos. Torcuato
dice que los primos como sistema físico "son una categoría completamente nueva de estructuras". Los investigadores han llamado a este nuevo patrón tipo fractal "periodicidad límite efectiva".
La figura consiste en una secuencia periódica de picos brillantes que reflejan los intervalos de números primos más comunes: todos son impares (excepto 2), muchos uno al lado del otro. Los picos más brillantes (pares separados por dos dígitos) se alternan a intervalos regulares con picos menos brillantes, reflejando números primos separados por seis dígitos. Entre ellos hay picos incluso más débiles que corresponden a pares de primos más distantes, etc. Todo esto es un número infinito de picos de Bragg colocados uno dentro del otro.
Una estructura similar de los picos de Bragg se observó anteriormente, en los patrones de difracción de cuasicristales.
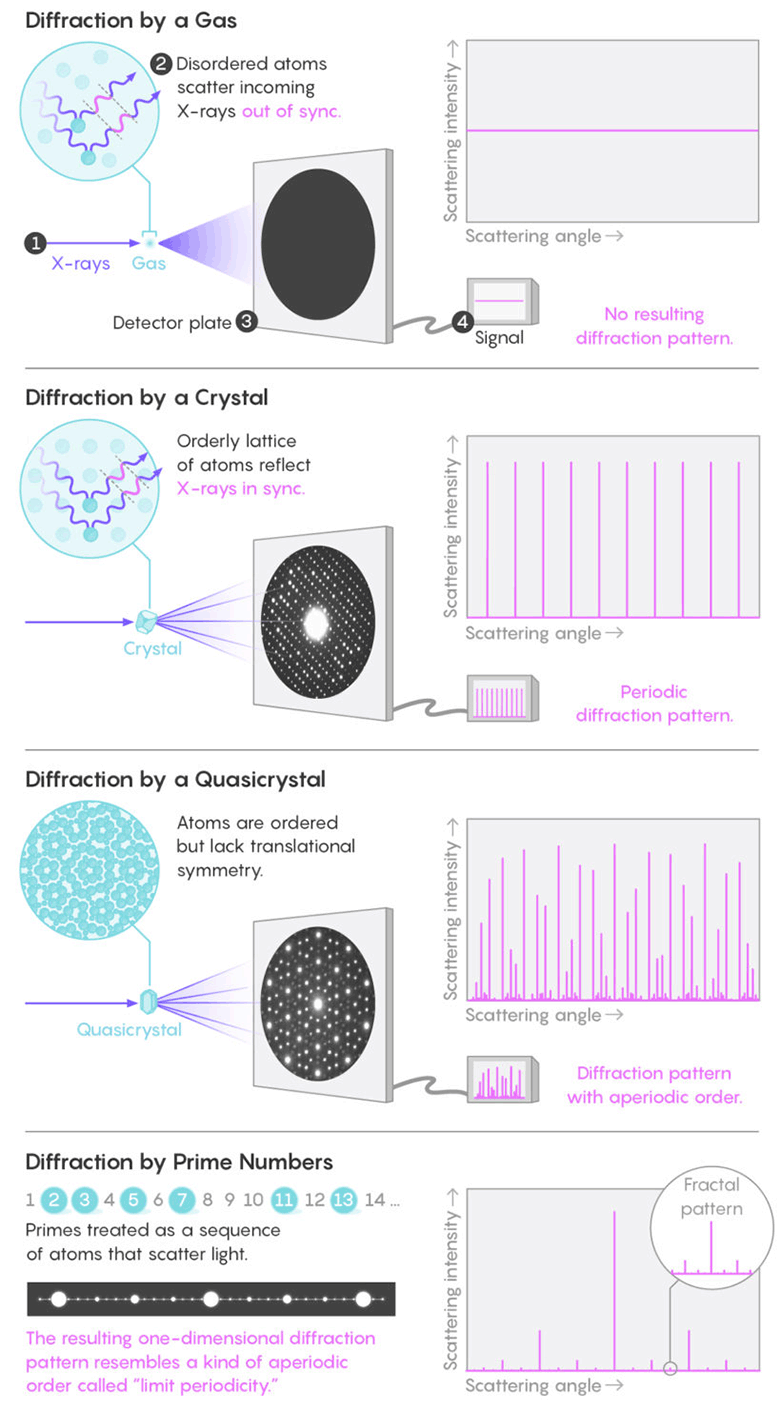Las moléculas aleatorias en líquidos o gases reflejan los rayos en todas las direcciones sin crear un patrón notable. Pero los átomos ubicados simétricamente en un cristal reflejan sincrónicamente las ondas de luz, creando puntos brillantes periódicos de difracción pronunciada. Al final resultó que, el patrón de distribución de primos forma un patrón de difracción fractal, similar al de los cuasicristales.Los cuasicristales son materiales extraños descubiertos en la década de 1980. Se caracterizan por la simetría prohibida en la cristalografía clásica y la presencia de un orden de largo alcance. Los mosaicos aperiódicos del tipo del famoso
mosaico de Penrose son un modelo matemático de cuasicristales. En estos mosaicos, la simetría traslacional está ausente, la repetibilidad y la cuasicristalinidad están presentes (simetría de quinto orden).
Fragmento de mosaico de Penrose tipo P1 (de azulejos de seis tipos)En el caso de los números primos, las distancias entre los picos son proporcionales entre sí, en contraste con los picos de cuasicristales Bragg espaciados irracionalmente. "Los números primos en realidad implican un estado completamente diferente de las posiciones de las partículas, similar a los cuasicristales, pero no como los cuasicristales",
dijo Torcuato.
El descubrimiento del patrón de difracción no puede llamarse un descubrimiento revolucionario para la teoría de números, porque la mayor parte de estos patrones ya se han descrito previamente, solo por otros métodos matemáticos (no a través de la difracción de cuasicristales). Entonces, usando el patrón de difracción, es posible predecir "dobles" de los tipos 17 y 19; este es el equivalente matemático de la
primera hipótesis de Hardy-Littlewood con respecto a la existencia de tuplas de números primos en un segmento dado de la recta numérica. Una de las reglas prohíbe trillizos de números impares consecutivos después de {3, 5, 7}. Esto también explica por qué el siguiente pico de Bragg más brillante en el patrón de difracción corresponde a números separados por seis dígitos en lugar de cuatro.
Un nuevo trabajo científico es solo una nueva mirada al problema de la distribución uniforme de números primos y una forma más fácil de derivar una cierta "ley única" para ellos. Además, esta es una forma inusual de analizar un problema matemático desde el punto de vista de la cristalografía, es decir, desde el punto de vista de un campo de investigación relativamente joven llamado "orden aperiódico", que estudia modelos no repetitivos y se encuentra en la intersección de la cristalografía, los sistemas dinámicos, el análisis armónico y la geometría discreta. Esta rama de la ciencia creció después del descubrimiento de cuasicristales, cuando quedó claro que los viejos métodos no funcionaban aquí.
La distribución de números primos se asemeja a un orden aperiódico especial, conocido desde la década de 1950. Se llama periodicidad límite. En tales sistemas, los intervalos periódicos se anidan en una jerarquía infinita, de modo que en cualquier intervalo, el sistema contiene partes de patrones que se repiten solo en un intervalo mayor, como en el mosaico de Taylor-Sokolar.
Azulejo Taylor-SokolarLos cálculos teóricos muestran que las fases periódicas máximas de una sustancia deberían poder formarse en la naturaleza, y tales sistemas pueden tener propiedades inusuales. Pero nadie supuso conectar la periodicidad limitante con los números primos. Ahora sabemos que existe tal conexión, y los números primos demuestran un nuevo tipo de periodicidad límite: la periodicidad límite “efectiva”, porque el sincronismo en las distancias entre los números primos en todo el sistema solo se observa estadísticamente.
Surge la pregunta: ¿cómo pueden los patrones en la distribución de números primos afectar la fuerza de los algoritmos criptográficos?
“Recibo muchas cartas sobre este tema. Aunque este es un estudio interesante, no tiene nada que ver con la criptografía ”,
escribió el famoso criptógrafo Bruce Schneier en su blog. - Los criptógrafos no están interesados en encontrar números primos o incluso su distribución. La persistencia de los algoritmos de criptografía de clave pública de tipo RSA está asociada con la dificultad de factorizar números compuestos grandes, que son producto de números primos. Y este es un asunto completamente diferente ".
Entonces, a pesar del progreso en el estudio de la distribución de números primos, no hay necesidad de preocuparse por la fuerza de los códigos criptográficos todavía.
