Problemas de la escritura moderna de textos matemáticos.

En un artículo reciente, el camarada KvanTTT planteó la pregunta :

¿Puede explicar lo que no le gusta de las fórmulas modernas (enunciados matemáticos y) y cómo se puede mejorar?

Traté de responder en un comentario, pero el tamaño del campo de texto no me permitió terminar los cálculos. Este artículo es una respuesta demasiado detallada.

Debo decir que el material es holivarny. En parte demasiado emocional. Muy controvertido Demasiado personal: a menudo basado en la experiencia personal, no rico, aunque diverso. La publicación se relaciona con los libros de texto escolares y universitarios: la literatura "profesional" tiene sus propios detalles, su propia audiencia . No hay solución al problema en las realidades actuales. Al mismo tiempo, algunas de mis observaciones mucho antes que yo fueron expresadas por autoridades como Knut y Hamming; chicos un poco menos populares incluso apuntaron la instrucción " Cómo leer matemáticas ".

Entonces, en mi opinión, la queja principal no es tanto escribir fórmulas como presentar un material . Además, a la presentación de material en casi todos los niveles de educación, comenzando desde la escuela y terminando con la ciencia avanzada. El comienzo de la situación actual fue establecido por Euclides, quien declaró la ausencia del camino real en matemáticas. El camino real no ha sido pavimentado hasta ahora. Euclides lo hizo, y nosotros podemos.

El primer problema es la importancia no se muestra . Otro regalo de Euclides: "Déle al centavo un centavo si está buscando beneficios, no matemáticas". Los autores comienzan a introducir definiciones, probar teoremas y hacer otras matemáticas sin explicar por qué es necesario. Ejemplo: un libro de texto sobre análisis matemático de Fichtenholtz . Lea el primer capítulo: "del curso escolar conoce los números racionales, pero las necesidades de las matemáticas nos obligan a introducir números reales ..." y comenzó. ¿Cuáles son las necesidades, qué tipo de matemática, por qué son racionales, no felices? Sí, el perro lo conoce. "Obviamente".

O otro ejemplo del mismo tutorial. "El número constante a se llama límite de opciones $$ si por cada positivo $$ no importa cuán pequeño sea, existe un número N tal que todos los valores $$ para el cual el número n> N satisface la igualdad $$ . "

La mayoría de los estudiantes no entienden la definición anterior, pero después de seis meses se acostumbran. Incluso más estudiantes, incluso hacia el final de sus estudios, no son conscientes de por qué necesitan el concepto del límite de secuencia. Del mismo modo para funciones, integrales, series ... Fichtenholtz describe algunos objetos matemáticos, a veces da ejemplos particulares, y eso es todo. Bueno, sí, ahora entiendo que los límites son necesarios, por ejemplo, para la descripción correcta de las sumas superior / inferior al introducir integrales, ¡pero antes de las integrales dos semestres más!

O un determinante definido como una función multilineal sesgada simétrica. Chicos, ¿hablas en serio? ¿La única respuesta adecuada de un estudiante de primer año a tal definición de "y qué"? ¿Cuál es el beneficio de esta definición? No discuto, hay un beneficio, pero ¿puede alguien de primer año ser consciente de ello?

Falsa solución al problema : antecedentes. Aparece en todo tipo de conferencias. "El problema fue planteado por Jacob, examinado por su discípulo Abel, y el discípulo del discípulo Caín, y ciento quinientas encarnaciones de Vishnu". ¿Cuál es la esencia del problema, por qué fue resuelto por el autor original, por qué es tan importante matar horas de profesor? Se omite.

El siguiente problema: los autores no plantean problemas reales

En principio, es similar al anterior. Recuerda el curso de la teoría de la probabilidad. ¿Qué tareas prevalecen allí? "Hay 25 bolas negras y 10 blancas en la canasta ..." Ejemplos de casino, cartas, D&D, económicos - no, no escuchados. Utilizaremos los ejemplos más políticamente correctos, aunque la teoría de la probabilidad ha surgido de la investigación de dados.

Acerca de ejemplos en vivo recientemente escribió Free_Mic_RS


Las matemáticas comienzan con una tarea. Y las tareas muertas y unilaterales dejan la impresión de que la teoría solo funciona con ellas. La intención de los autores es buena: dar un ejemplo y luego pasar a lo general. Resumen del ejemplo. Pero unos pocos ejemplos "vivos" harían la transición a la abstracción mucho más útil. Al menos, creo firmemente que el proceso inverso (la transición de lo abstracto a lo particular) sería mucho más fácil.

Problema: brevedad excesiva e inconsistencia

¿Recuerdas la escuela? ¿Qué pasa con la fórmula discriminante? ¿Y cómo se prueba / deriva? Una forma: puramente algebraica . Tomamos la ecuación $$ , "Multiplica cada parte por $$ y agrega $$ "( ¿Por qué precisamente estos valores? ), Algunas transformaciones más, y ya está. Después de discriminante, los estudiantes reciben discriminante por incluso b. Y luego las fórmulas de Vieta. Y también cuadrados completos. Y un montón de ejemplos. Y lejos de explicar siempre por qué se necesitan todos estos métodos.

Ahora imagine la situación, se le dice al alumno: "hoy aprenderemos cómo resolver ecuaciones con $$ . Cualquiera ". Y una serie de ejemplos comienza con una complicación.

$$

Una gran cantidad de ejemplos que conducen orgánicamente a la solución de la ecuación a través de cuadrados completos. Luego puede ingresar el discriminante (como un algoritmo simple para resolver ecuaciones cuando los estudiantes se cansan de resaltar los cuadrados completos), y Viet con un discriminante uniforme como "know-how".

Un enfoque similar se utiliza en los libros de texto. Por desgracia, no en todos. Y no en todas partes se ve una secuencia clara. Según los rumores, algunos autores perdieron hojas de borradores en los tranvías y luego reemplazaron las piezas perdidas con expresiones como "es fácil mostrar que ...". Como resultado, en lugar de saltos tranquilos de un ejemplo a otro, los estudiantes se vieron obligados a saltar sobre el abismo. ¿Cuántas personas rompieron y aún se rompen por 10 + 6 años de escolaridad / universidad?

Ejemplo personal (solicitado en la publicación original). En el primer año de matan, sufrí. En silencio resolviendo los ejemplos, no aprendió la teoría en absoluto. Le pedí ayuda a un compañero de clase para calcular la longitud de la curva a través de la integral. Tomó una botella de cerveza, dibujó una curva aleatoria, la enderezó con segmentos infinitamente pequeños, seleccionó uno de esos segmentos, la construyó hasta el triángulo dl, dx, dy y preguntó: "¿Recuerdas el teorema de Pitágoras"? Entonces todo fue simple.



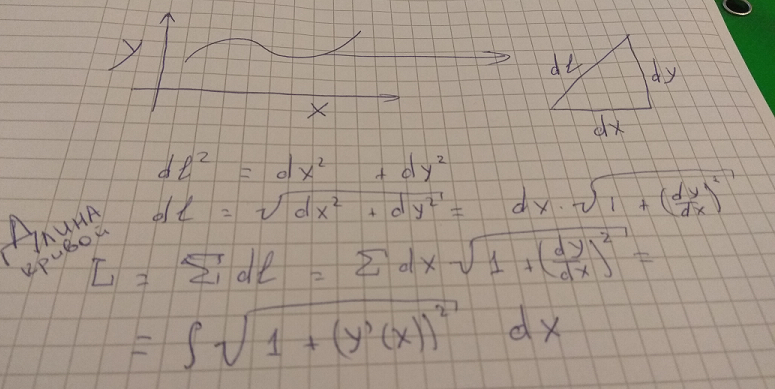
Le pregunté: ¿por qué esto no se muestra en pares / en libros de texto? Mostró un par de contraejemplos, explicó por qué se necesita formalismo en Matan, y me atasqué. Acabo de leer el teorema, destaqué lo principal, escribí / resolví ejemplos triviales, luego me ocupé del formalismo y realmente entendí lo que estaba sucediendo.

No sé si es posible utilizar de forma masiva el enfoque general general => contraejemplos => formalismo . No sé cuánto y qué teoría / práctica necesita ganar un estudiante antes del "avance", apenas puedo imaginar cómo poner experimentos pedagógicos sobre este tema, y ​​cuánto trabajo tendré que invertir en investigación. Pero el recuerdo de esa explicación ha estado viviendo durante 10 años. Y después de todos estos años, primero trato de darle al público una visión general, luego mostrar los problemas y luego sumergirme en los detalles.

Dirás que mis sentimientos personales pueden estar equivocados. Además de ellos, solo tengo ideas similares de Hamming :

... podría estudiar qué métodos fueron efectivos y cuáles no. Al asistir a las reuniones, ya estudié por qué algunos trabajos son recordados, y la mayoría no. Una persona técnica quiere dar una conferencia técnica muy limitada. Como regla general, la audiencia quiere una conferencia amplia de carácter general y quiere una visión general mucho más general e introducciones de las que el orador quiere dar. Como resultado, muchas conferencias son ineficaces. El profesor llama al tema y de repente se sumerge en los detalles. Pocas personas pueden seguir la pista. Debe dibujar una imagen general para decir por qué esto es importante, y luego desplegar lentamente un bosquejo de lo que se hizo. Luego, más personas dirán: "Sí, Joe lo hizo" o "Mary hizo lo que realmente veo de qué se trata. Sí, Mary dio una muy buena conferencia, entiendo lo que hizo ". Como regla, las personas dan una conferencia muy limitada y segura; Suele ser ineficaz. Además, muchas conferencias están llenas de información ...

Ideas a granel

Debo decir que mi experiencia en la enseñanza es extremadamente limitada. Puede que hayas notado que me limité al currículum escolar y al matanaliz. Por desgracia, estas son áreas donde tuve la oportunidad de poner la teoría en contacto con la práctica. Todavía no entiendo la esencia del determinante en álgebra, no me doy cuenta de la geometría proyectiva, y solo hace seis meses comencé a penetrar en las matrices (justo después de la práctica, eh). Una buena ilustración del dicho "la teoría sin práctica está muerta".

Como me dijeron, en NMU siempre se ha introducido un nuevo concepto con una docena de preguntas. ¿Y si es así? ¿Y si esta cláusula no se cumple? ¿Qué se necesita para complementar nuestro concepto a un semigrupo? A los oyentes se les permitió jugar con el tema. Acostúmbrate a ello. Creo que vale la pena pensar detenidamente sobre la experiencia de NMU.

Seguramente, en las ramas superiores de las matemáticas, el enfoque "primero un ejemplo, luego una abstracción" no funcionará. Por lo tanto, los ejemplos en una hoja de papel no ayudan a realizar RSA. Pero el creciente tiempo del programa con el aumento de la longitud de la clave ayuda a sentir los aspectos puramente prácticos.

Existe el temor de que los libros escolares "ideales / de efecto invernadero" causen conmoción al trabajar con la "torre". Parece que "un trabajador incondicional necesita ser educado desde una edad temprana".

Es bastante difícil desarrollar cursos, esperando que los estudiantes ya sepan algo. Cuanto mayor sea la base requerida, más probable es que el alumno no entienda algo de la base.

Dicen que el pico de la forma de los matemáticos tiene 30 años. Después de los 30, ya puede cargarlos para escribir libros de texto, dándole a un compañero un metodólogo especialista.

La tecnología actual le permite escribir textos usando git. Un artículo sobre la compilación de TeXa en pdf en el proceso de CI recientemente se deslizó en un hub Estoy seguro de que un equipo de autores con buenas herramientas puede escribir libros de texto mucho mejores.

Además de profesores, maestros, estudiantes y escolares, hay estados en matemáticas. Y regulaciones. Y los requisitos. Y certificación. Todo esto afecta los libros de texto, autores, maestros y la calidad del material.

Cómo mejorar el flujo de material en textos matemáticos.

En las realidades actuales (rusas), nada. Hay entusiastas, hay profesionales, no hay motivación.

Los profesores de matemáticas tienen suficientes tareas para escribir libros de texto. A veces no hay suficientes habilidades puramente humanitarias; los libros no se enseñan en las universidades. Además, la deformación profesional: lo "obvio" para un profesor puede ser abrumador para los estudiantes. Los maestros de matemáticas están ocupados. Y papeles. Y tutoría. No diré nada sobre el estado. Casi no se encontró con sus representantes, por lo que no hay nada que decir. A menos que mencione la política de reemplazar los libros de texto cada tres años. Después de la escuela, quería llevar mis libros de texto a la biblioteca, me dijeron "son viejos, no puedes quedarte con ellos". La motivación para escribir buenos libros de texto no agrega este enfoque.

En otras palabras, personalmente no espero un progreso positivo del sistema educativo. Espero, por supuesto, pero no espero. Lo que ayuda son vislumbres de TI y otras ingenierías. En una de las conferencias matemáticas, recibí un libro sobre gráficos de computadora de uno de los participantes. El autor trabajó en una oficina desarrollando un núcleo gráfico de algún sistema de dibujo, y el material fue bastante bueno. La matemática no era "pura", aplicada, pero el hecho de la existencia de un buen material educativo fue ciertamente agradable.

Otro enfoque: docentes de empresas que trabajan en universidades. No se pueden esperar textos matemáticos de estos tipos, los detalles no son los mismos. A menos que los desarrolladores de juegos escriban un manual sobre la teoría, o los gráficos escribirán sobre el álgebra / geometría necesaria para desarrollar los mismos sistemas CAD (si hay tales proyectos, llame) .

Finalmente, hay varias plataformas educativas no estatales, como el mismo Coursera. Estos tipos pueden hacer cualquier cosa, porque trabajan por dinero, compiten y reciben comentarios rápidamente. Pero tienen su propio inconveniente: el formato para enviar datos es diferente. No escriben textos directamente.

¿Y qué vendrá todo en el futuro?

Lo mas interesante. Tal vez todo permanecerá como está. Tal vez habrá una desviación de los textos en matemáticas. O tal vez los autores se inspirarán en la idea "el texto del producto debe ser conveniente para el cliente del lector ", y los pioneros podrán romper la tradición. Luego, en 30-50-100 años tendremos libros de texto que sean comprensibles para la mayoría de los lectores.

Upd1. Inserté una foto con el cálculo de la longitud de la sección de la curva.

Upd2. En los comentarios a menudo se menciona que el texto está dedicado a los problemas de la enseñanza, y no a las matemáticas profesionales. La razón es simple: la mayor parte del trabajo "profesional" que he visto en términos de presentación de material no difiere de los libros de texto. Al mismo tiempo, la literatura de la escuela / universidad es conocida por la mayoría en el habr, y "profesional" por ciento.