Hola a todos! Este artículo se centrará en una parte importante del procesamiento de señal digital: el filtrado de señal de ventana, en particular en FPGA. El artículo mostrará cómo diseñar ventanas clásicas de longitud estándar y ventanas "largas" de 64K a 16M + muestras. El lenguaje de desarrollo principal es VHDL, la base del elemento son los últimos cristales Xilinx FPGA de las últimas familias: estos son Ultrascale, Ultrascale +, 7-series. El artículo demostrará la implementación de CORDIC, el núcleo básico para configurar funciones de ventana de cualquier duración, así como funciones básicas de ventana. El artículo describe el método de diseño utilizando lenguajes de alto nivel C / C ++ en Vivado HLS. Como de costumbre, al final del artículo encontrará un enlace a los códigos fuente del proyecto.
KDPV: un esquema típico de transmisión de señal a través de nodos DSP para tareas de análisis de espectro.
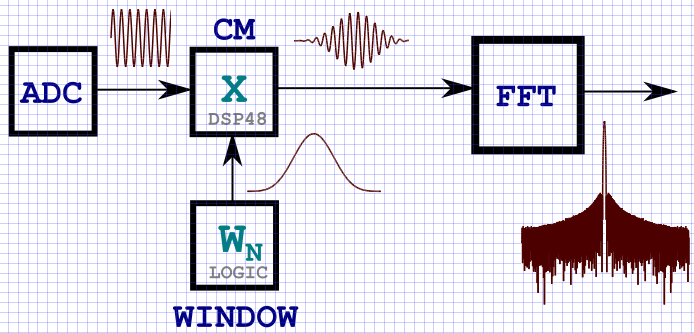
Introduccion
Del curso "Procesamiento de señal digital" muchas personas saben que para una forma de onda sinusoidal que es infinita en el tiempo, su espectro es una función delta en la frecuencia de la señal. En la práctica, el espectro de una señal armónica limitada en tiempo real es equivalente a la función
~ sin (x) / x , y el ancho del lóbulo principal depende de la duración del intervalo de análisis de señal
T. El límite de tiempo no es más que multiplicar la señal por una envoltura rectangular. Se sabe por el curso DSP que la multiplicación de señales en el dominio del tiempo es una convolución de sus espectros en el dominio de la frecuencia (y viceversa), por lo tanto, el espectro de la envoltura rectangular limitada de la señal armónica es equivalente a ~ sinc (x). Esto también se debe al hecho de que no podemos integrar la señal en un intervalo de tiempo infinito, y la transformada de Fourier en forma discreta, expresada a través de una suma finita, está limitada por el número de muestras. Como regla general, la longitud de la FFT en los modernos dispositivos de procesamiento digital FPGA lleva los valores de
NFFT de 8 a varios millones de puntos. En otras palabras, el espectro de la señal de entrada se calcula en el intervalo
T , que en muchos casos es igual a
NFFT . Al limitar la señal al intervalo
T , imponemos una "ventana" rectangular con una duración de
T muestras. Por lo tanto, el espectro resultante es el espectro de la señal armónica multiplicada y la envolvente rectangular. En las tareas DSP, se han inventado ventanas de varias formas durante mucho tiempo, que, cuando se superponen a una señal en el dominio del tiempo, pueden mejorar sus características espectrales. Una gran cantidad de varias ventanas se debe principalmente a una de las características principales de cualquier superposición de ventanas. Esta característica se expresa en la relación entre el nivel de los lóbulos laterales y el ancho del lóbulo central. Un patrón bien conocido: cuanto más fuerte es la supresión de los lóbulos laterales, más ancho es el lóbulo principal y viceversa.
Una de las aplicaciones de las funciones de ventana: detección de señales débiles en el contexto de las más fuertes al suprimir el nivel de los lóbulos laterales. Las funciones de la ventana principal en las tareas de DSP son una ventana triangular, sinusoidal, Lanczos, Hann, Hamming, Blackman, Harris, Blackman-Harris, ventana plana, ventana Natall, Gauss, Kaiser y muchas otras. La mayoría de ellos se expresan a través de una serie finita sumando señales armónicas con pesos específicos. Las ventanas de forma compleja se calculan tomando un exponente (ventana de Gauss) o una función Bessel modificada (ventana de Kaiser), y no se considerarán en este artículo. Puede leer más sobre las funciones de ventana en la literatura, que tradicionalmente daré al final del artículo.
La siguiente figura muestra las funciones de ventana típicas y sus características espectrales construidas con las herramientas CAD de Matlab.

Implementación
Al comienzo del artículo, inserté KDPV, que muestra en términos generales un diagrama estructural de la multiplicación de datos de entrada por una función de ventana. Obviamente, la forma más fácil de implementar el almacenamiento de una función de ventana en el FPGA es escribirlo en la memoria (bloquear
RAMB o distribuido
distribuido , no importa mucho), y luego recuperar cíclicamente los datos cuando llegan las muestras de entrada de la señal. Como regla general, en los FPGA modernos, la cantidad de memoria interna permite almacenar funciones de ventana de tamaños relativamente pequeños, que luego se multiplican con las señales de entrada entrantes. Por pequeño quiero decir funciones de ventana de hasta 64K muestras de largo.
Pero, ¿qué pasa si la función de ventana es demasiado larga? Por ejemplo, 1M de lecturas. Es fácil calcular que para dicha función de ventana presentada en una cuadrícula de bits de 32 bits, se requieren NRAMB = 1024 * 1024 * 32/32768 = 1024 celdas de memoria de bloque de los cristales de RAMGA36K tipo FPGA Xilinx. ¿Y para 16 millones de muestras? ¡16 mil celdas de memoria! Ni un solo FPGA moderno tiene tanta memoria. Para muchos FPGA esto es demasiado, y en otros casos es un uso derrochador de recursos FPGA (y, por supuesto, el dinero del cliente).
A este respecto, debe encontrar un método para generar muestras de funciones de ventana directamente al FPGA sobre la marcha, sin escribir coeficientes desde el dispositivo remoto en la memoria de bloque. Afortunadamente, las cosas básicas han sido inventadas por mucho tiempo para nosotros. Usando un algoritmo como
CORDIC (el método
dígito a dígito ), es posible diseñar muchas funciones de ventana cuyas fórmulas se expresan en términos de señales armónicas (Blackman-Harris, Hann, Hamming, Nattal, etc.)
CORDIC
CORDIC es un método iterativo simple y conveniente para calcular la rotación de un sistema de coordenadas, que le permite calcular funciones complejas realizando operaciones de suma y desplazamiento primitivas. Usando el algoritmo CORDIC, uno puede calcular los valores de las señales armónicas sin (x), cos (x), encontrar la fase - atan (x) y atan2 (x, y), funciones trigonométricas hiperbólicas, rotar el vector, extraer la raíz del número, etc.
Al principio, quería tomar el núcleo CORDIC terminado y reducir la cantidad de trabajo, pero me disgustan mucho los núcleos Xilinx. Después de estudiar los repositorios en el github, me di cuenta de que todos los núcleos presentados no son adecuados por varias razones (mal documentados e ilegibles, no universales, hechos para una tarea específica o base de elementos,
escritos en verilog , etc.). Luego le pedí al compañero
lazifo que hiciera este trabajo por mí. Por supuesto, lo hizo frente, porque la implementación de CORDIC es una de las tareas más simples en el campo de DSP. Pero como soy impaciente, en paralelo con su trabajo, escribí
mi bicicleta con mi
propio núcleo parametrizado. Las características principales son la profundidad de bits configurable de las señales de salida
DATA_WIDTH y la fase de entrada normalizada
PHASE_WIDTH de -1 a 1, y la precisión de los cálculos de
PRECISIÓN . El núcleo CORDIC se ejecuta de acuerdo con el circuito paralelo de la tubería: en cada ciclo de reloj, el núcleo está listo para realizar cálculos y recibir muestras de entrada. El núcleo gasta N ciclos para calcular la muestra de salida, cuyo número depende de la capacidad de las muestras de salida (cuanto más capacidad, más iteraciones para calcular el valor de salida). Todos los cálculos ocurren en paralelo. Por lo tanto, CORDIC es el núcleo base para crear funciones de ventana.
Funciones de ventana
En el marco de este artículo, me doy cuenta solo de esas funciones de ventana que se expresan a través de señales armónicas (Hann, Hamming, Blackman-Harris de varios órdenes, etc.). ¿Qué se necesita para esto? En términos generales, la fórmula para construir una ventana se parece a una serie de longitud finita.

Un cierto conjunto de coeficientes
a k y miembros de la serie determina el nombre de la ventana. La ventana más popular y de uso frecuente es la ventana Blackman-Harris: de diferente orden (de 3 a 11). La siguiente es una tabla de coeficientes para las ventanas Blackman-Harris:

En principio, el conjunto de ventanas Blackman-Harris es aplicable en muchos problemas de análisis espectral, y no hay necesidad de intentar usar ventanas complejas como Gauss o Kaiser. Las ventanas Nattal o planas son solo una variedad de ventanas con diferentes pesos, pero los mismos principios básicos que Blackman-Harris. Se sabe que cuantos más miembros de la serie, más fuerte es la supresión del nivel de los lóbulos laterales (sujeto a una elección razonable de la profundidad de bits de la función de ventana). En función de la tarea, el desarrollador solo tiene que elegir el tipo de ventanas utilizadas.
Implementación de FPGA - enfoque tradicional
Todos los núcleos de las funciones de ventana están diseñados utilizando el enfoque clásico para describir circuitos digitales en FPGA y están escritos en el lenguaje VHDL. A continuación se muestra una lista de los componentes realizados:
- bh_win_7term - Orden Blackman-Harris 7, una ventana con máxima supresión de andamios laterales.
- bh_win_5term : orden de Blackman-Harris 5, incluye una ventana con una parte superior plana.
- bh_win_4term - Blackman-Harris 4 pedidos, incluye la ventana Nattal y Blackman-Nattal.
- bh_win_3term - Blackman-Harris 3 pedidos,
- hamming_win : ventanas de Hamming y Hann.
El código fuente para el componente de ventana Blackman-Harris es de 3 órdenes de magnitud:
entity bh_win_3term is generic ( TD : time:=0.5ns;
En algunos casos, utilicé la biblioteca
UNISIM para incrustar los
nodos DSP48E1 y DSP48E2 en el proyecto, lo que finalmente
me permite aumentar la velocidad de los cálculos debido a la canalización dentro de estos bloques, pero como la práctica ha demostrado, es más rápido y fácil dar rienda suelta y escribir algo como
P = A * B + C y especifique las siguientes directivas en el código:
attribute USE_DSP of <signal_name>: signal is "YES";
Esto funciona bien y establece rígidamente el tipo de elemento en el que se implementa la función matemática para el sintetizador.
Vivado hls
Además, implementé todos los núcleos utilizando las herramientas
Vivado HLS . Enumeraré las principales
ventajas de Vivado HLS: alta velocidad de diseño (
tiempo de comercialización ) en lenguajes de alto nivel C o C ++, modelado rápido de nodos desarrollados debido a la falta de un concepto de frecuencia de reloj, configuración flexible de soluciones (en términos de recursos y rendimiento) mediante la introducción pragmas y directivas en el proyecto, así como un umbral de entrada bajo para desarrolladores en lenguajes de alto nivel. La principal desventaja es el costo subóptimo de los recursos de FPGA en comparación con el enfoque clásico. Además, no es posible alcanzar esas velocidades proporcionadas por los antiguos métodos RTL clásicos (VHDL, Verilog, SV). Bueno, el mayor
inconveniente es bailar con una pandereta, pero esto es característico de todos los CAD de Xilinx. (Nota: en el depurador Vivado HLS y en el modelo C ++ real, a menudo se obtuvieron resultados diferentes, porque Vivado HLS funciona de manera torcida utilizando las ventajas de la
precisión arbitraria ).
La siguiente imagen muestra el registro del núcleo CORDIC sintetizado en Vivado HLS. Es bastante informativo y muestra mucha información útil: la cantidad de recursos utilizados, la interfaz de usuario del núcleo, los bucles y sus propiedades, el retraso en la computación, el intervalo para calcular el valor de salida (importante al diseñar circuitos en serie y en paralelo):

También puede ver la forma de calcular datos en varios componentes (funciones). Se puede ver que en la fase cero, se leen los datos de la fase, y en los pasos 7 y 8, se muestra el resultado del nodo CORDIC.

El resultado de Vivado HLS: un núcleo RTL sintetizado creado a partir del código C. El registro muestra que en el análisis de tiempo, el núcleo pasa con éxito todas las restricciones:

Otra gran ventaja de Vivado HLS es que para verificar el resultado, ella misma realiza un banco de pruebas del código RTL sintetizado en función del modelo que se utilizó para verificar el código C. Esta puede ser una prueba primitiva, pero creo que es lo suficientemente genial y conveniente para comparar el funcionamiento del algoritmo en C y en HDL. A continuación se muestra una captura de pantalla de Vivado que muestra una simulación del modelo de función del núcleo de una función de ventana obtenida por Vivado HLS:

Por lo tanto, para todas las funciones de la ventana, se obtuvieron resultados similares, independientemente del método de diseño, en VHDL o en C ++. Sin embargo, en el primer caso, se logra una mayor frecuencia de operación y un menor número de recursos, y en el segundo caso, se logra la velocidad máxima de diseño. Ambos enfoques tienen derecho a la vida.
Calculé específicamente cuánto tiempo dedicaría al desarrollo utilizando diferentes métodos. Implementé un proyecto C ++ en Vivado HLS ~ 12 veces más rápido que en VHDL.
Comparación de enfoques
Compare el código fuente de HDL y C ++ para el núcleo CORDIC. El algoritmo, como se dijo anteriormente, se basa en las operaciones de suma, resta y desplazamiento. En VHDL, se ve así: hay tres vectores de datos: uno es responsable de la rotación del ángulo y los otros dos determinan la longitud del vector a lo largo de los ejes X e Y, que es equivalente a sin y cos (ver la imagen de la wiki):
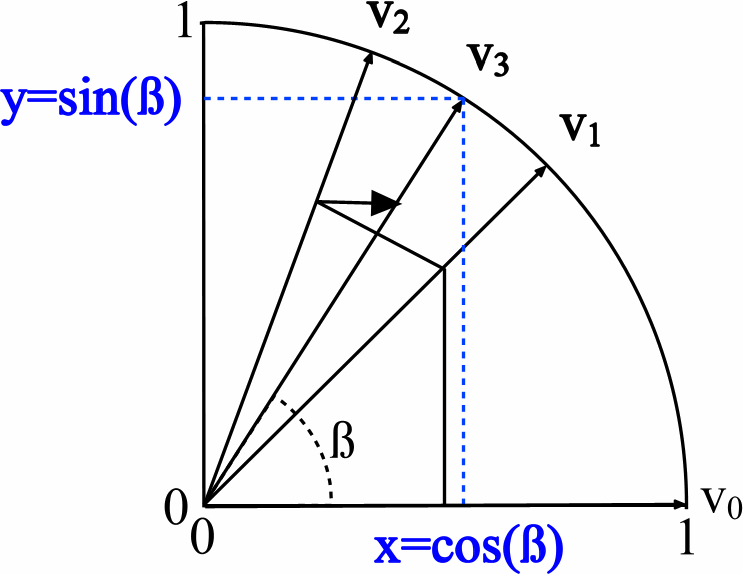
Al calcular iterativamente el valor Z, los valores X e Y se calculan en paralelo. El proceso de búsqueda cíclica de valores de salida en HDL:
constant ROM_LUT : rom_array := ( x"400000000000", x"25C80A3B3BE6", x"13F670B6BDC7", x"0A2223A83BBB", x"05161A861CB1", x"028BAFC2B209", x"0145EC3CB850", x"00A2F8AA23A9", x"00517CA68DA2", x"0028BE5D7661", x"00145F300123", x"000A2F982950", x"000517CC19C0", x"00028BE60D83", x"000145F306D6", x"0000A2F9836D", x"0000517CC1B7", x"000028BE60DC", x"0000145F306E", x"00000A2F9837", x"00000517CC1B", x"0000028BE60E", x"00000145F307", x"000000A2F983", x"000000517CC2", x"00000028BE61", x"000000145F30", x"0000000A2F98", x"0000000517CC", x"000000028BE6", x"0000000145F3", x"00000000A2FA", x"00000000517D", x"0000000028BE", x"00000000145F", x"000000000A30", x"000000000518", x"00000000028C", x"000000000146", x"0000000000A3", x"000000000051", x"000000000029", x"000000000014", x"00000000000A", x"000000000005", x"000000000003", x"000000000001", x"000000000000" ); pr_crd: process(clk, reset) begin if (reset = '1') then
En C ++, en Vivado HLS, el código se ve casi igual, pero el registro es varias veces más corto:
Aparentemente, se usa el mismo ciclo con turno y adiciones. Sin embargo, de forma predeterminada, todos los bucles en Vivado HLS están "colapsados" y se ejecutan secuencialmente, según lo previsto para el lenguaje C ++. La introducción del
pragma HLS UNROLL o
HLS PIPELINE convierte los cálculos en serie en paralelos. Esto conduce a un aumento en los recursos de FPGA, sin embargo, le permite calcular y enviar nuevos valores al núcleo en cada ciclo de reloj.
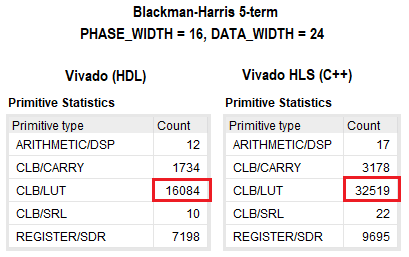
Los resultados de la síntesis del proyecto en VHDL y C ++ se presentan en la figura a continuación. Como puede ver, lógicamente, la diferencia es dos veces a favor del enfoque tradicional. Para otros recursos de FPGA, la discrepancia es insignificante. No profundicé en la optimización del proyecto en C ++, pero sin ambigüedades al establecer varias directivas o cambiar parcialmente el código, se puede reducir la cantidad de recursos utilizados. En ambos casos, los tiempos convergieron para una frecuencia central dada de ~ 350 MHz.
Características de implementación
Dado que los cálculos se realizan en un formato de punto fijo, las funciones de ventana tienen una serie de características que deben tenerse en cuenta al diseñar sistemas DSP en FPGA. Por ejemplo, cuanto mayor sea la profundidad de bits de los datos de la función de ventana, mejor será la precisión de la superposición de la ventana. Por otro lado, con una profundidad de bits insuficiente de la función de ventana, se introducirán distorsiones en la forma de onda resultante, lo que afectará la calidad de las características espectrales. Por ejemplo, una función de ventana debe tener al menos 20 bits cuando se multiplica por una señal con una duración de 2 ^ 20 = 1M muestras.
Conclusión
Este artículo muestra una forma de diseñar funciones de ventana sin usar memoria externa o memoria de bloque FPGA. Se da el método de usar recursos exclusivamente lógicos de FPGA (y en algunos casos bloques DSP). Usando el algoritmo CORDIC, es posible obtener funciones de ventana de cualquier profundidad de bits (dentro de lo razonable), de cualquier longitud y orden, y por lo tanto tener un conjunto de prácticamente cualquier característica espectral de la ventana.
Como parte de uno de los estudios, logré obtener un núcleo de trabajo estable de la función de ventana Blackman-Harris de 5 y 7 órdenes de magnitud en muestras 1M a una frecuencia de ~ 375 MHz, y también hacer un generador de coeficientes rotativos para un FFT basado en CORDIC a una frecuencia de ~ 400 MHz. Cristal FPGA usado: Kintex Ultrascale + (xcku11p-ffva1156-2-e).
Enlace al
proyecto github aquí . El proyecto contiene un modelo matemático en Matlab, códigos fuente para funciones de ventana y CORDIC en VHDL, así como modelos de las funciones de ventana enumeradas en C ++ para Vivado HLS.
Artículos útiles
También aconsejo un libro muy popular sobre DSP:
Ayficher E., Jervis B. Procesamiento de señal digital. Enfoque prácticoGracias por su atencion!