Robomóviles sin conductores entregan pizza. Los taxis sin chófer transportan personas. Los camiones sin conductores llevan cargas de varias toneladas. Si analizamos todos estos proyectos espectaculares, llegaremos a diferentes tareas típicas, la más importante de las cuales es la búsqueda y optimización de rutas. Tales problemas se resuelven usando la
teoría de grafos . Este tema no es simple, se estudia principalmente en la universidad o, al menos, en clases especializadas de alto nivel. Pero en esta publicación, mostraré cómo usar el LEGO EV3 para aprender la teoría de gráficos ya en la escuela secundaria. Y sin abarrotar, pero a un nivel fascinante y aplicado.
 Transportador automotriz LAB EV3 de Danny Realmente colecciona autos LEGO. Pero no se trata poco de él.
Transportador automotriz LAB EV3 de Danny Realmente colecciona autos LEGO. Pero no se trata poco de él.Para que el transporte no tripulado llegue a donde se necesita, debe ser capaz de construir una ruta entre los puntos dados. El más corto y consistente con las reglas de tráfico es deseable. Para simular y resolver este problema, necesitamos la plataforma móvil LEGO EV3 y, de hecho, el mapa en el que se moverá esta plataforma.
Plataforma móvil LEGO EV3
Nuestra plataforma móvil debe estar equipada con sensores y servos. Todo lo que necesita se puede encontrar en el conjunto educativo básico de LEGO Mindstorms EV3 45544. Así es como se ve la plataforma:

El montaje no requiere conocimientos de electrónica y no lleva más de media hora. La plataforma tiene todo lo que necesita para alcanzar un alto nivel de abstracción al resolver un problema.
Hoja de ruta
Dibujemos una hoja de ruta en forma de cuadrícula. Las líneas son carreteras, los puntos de intersección son intersecciones de carreteras:
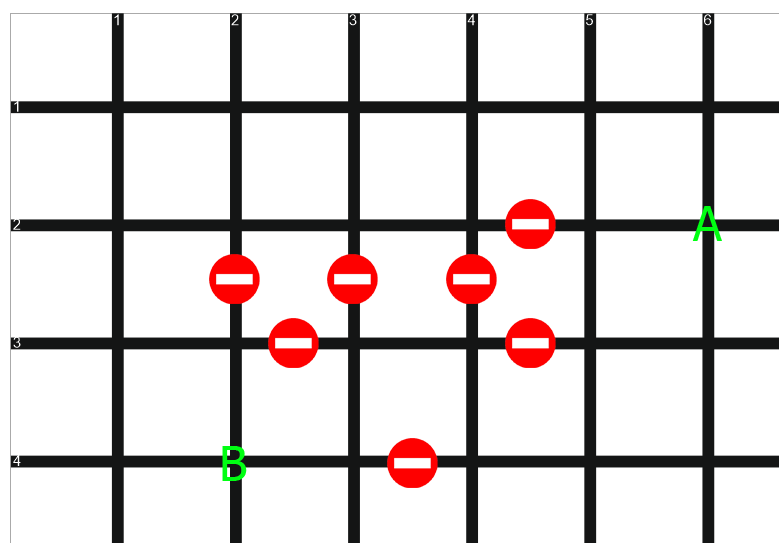
Todas las secciones de la carretera entre las intersecciones tienen la misma longitud, el tráfico en ellas es de dos vías. Algunas carreteras están bloqueadas, están marcadas con un "ladrillo". Además, todos los giros en nuestro mapa son múltiplos de 90 grados. La complicación de la red de carreteras no afectará el principio de resolver el problema, y para mayor claridad, lo haremos con una opción bastante simple. Nuestra tarea es conducir desde el punto A al punto B sobre el camino más corto.
Cuenta
Cada intersección tiene sus propias coordenadas: los números de línea horizontal y vertical. En la teoría de grafos, tales intersecciones se llaman
vértices . Las carreteras entre intersecciones se indican con flechas. En la teoría de grafos, estos son
bordes . Todos los caminos son bidireccionales (flechas en ambas direcciones) significa que el gráfico
no está
orientado . El costo (tiempo de viaje) es el mismo para todos los tramos de la carretera, lo que significa que el gráfico
no está
ponderado .

Matriz de adyacencia
El gráfico representado por la imagen muestra claramente el mapa y las conexiones dentro de él. Pero en una computadora, incluido EV3, es laborioso procesar información gráfica. Es óptimo codificar un gráfico con una matriz, una matriz de adyacencia.
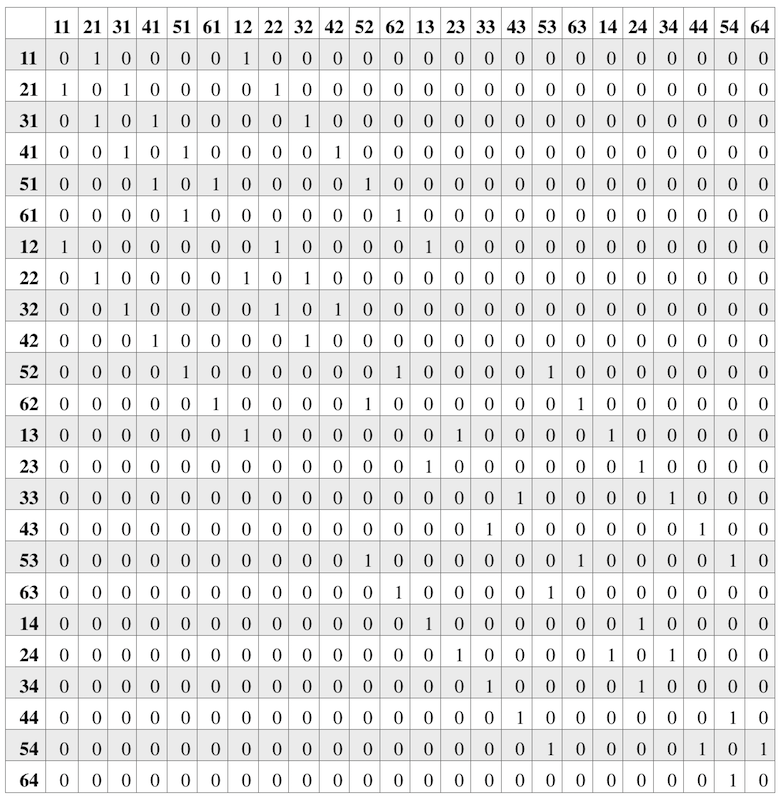
Si no hay una conexión directa entre las intersecciones, ponemos 0. Si la hay - 1. Si la hay - 1. Acordamos que todas las distancias entre las intersecciones adyacentes son iguales a 1. Si la gráfica fue ponderada, en lugar de la unidad en cada intersección pondríamos " peso "de la trama. Y si se tuviera en cuenta la dirección del movimiento, entonces la matriz anterior sería asimétrica: en una dirección podría ser 1 y en la otra 0.
Con una matriz de adyacencia, nuestro robot ya puede resolver el problema: encontrar la ruta más corta de A a B. Pero tenemos una matriz bidimensional, y en EV3 solo se pueden almacenar matrices unidimensionales. Podemos ir fácilmente a una matriz unidimensional a través del desplazamiento n * Y + X, donde n es el tamaño de la matriz.
Algoritmo de Dijkstra
El algoritmo de Dijkstra, el algoritmo para encontrar la ruta más corta entre un vértice de un gráfico y todos los demás, se utilizará para resolver. El algoritmo fue inventado en 1956 por el científico holandés Edsger Dijkstroy. Si la explicación es lo más simple posible, entonces el algoritmo se basa en el progreso secuencial a los vértices vecinos del gráfico con una evaluación constante de la distancia recorrida. Se puede encontrar un buen ejemplo ilustrativo y un diagrama de flujo básico del algoritmo en el artículo de Wikipedia.
En nuestro caso, el diagrama de flujo del algoritmo Dijkstra (nuestro "Dijkstra") se verá así:
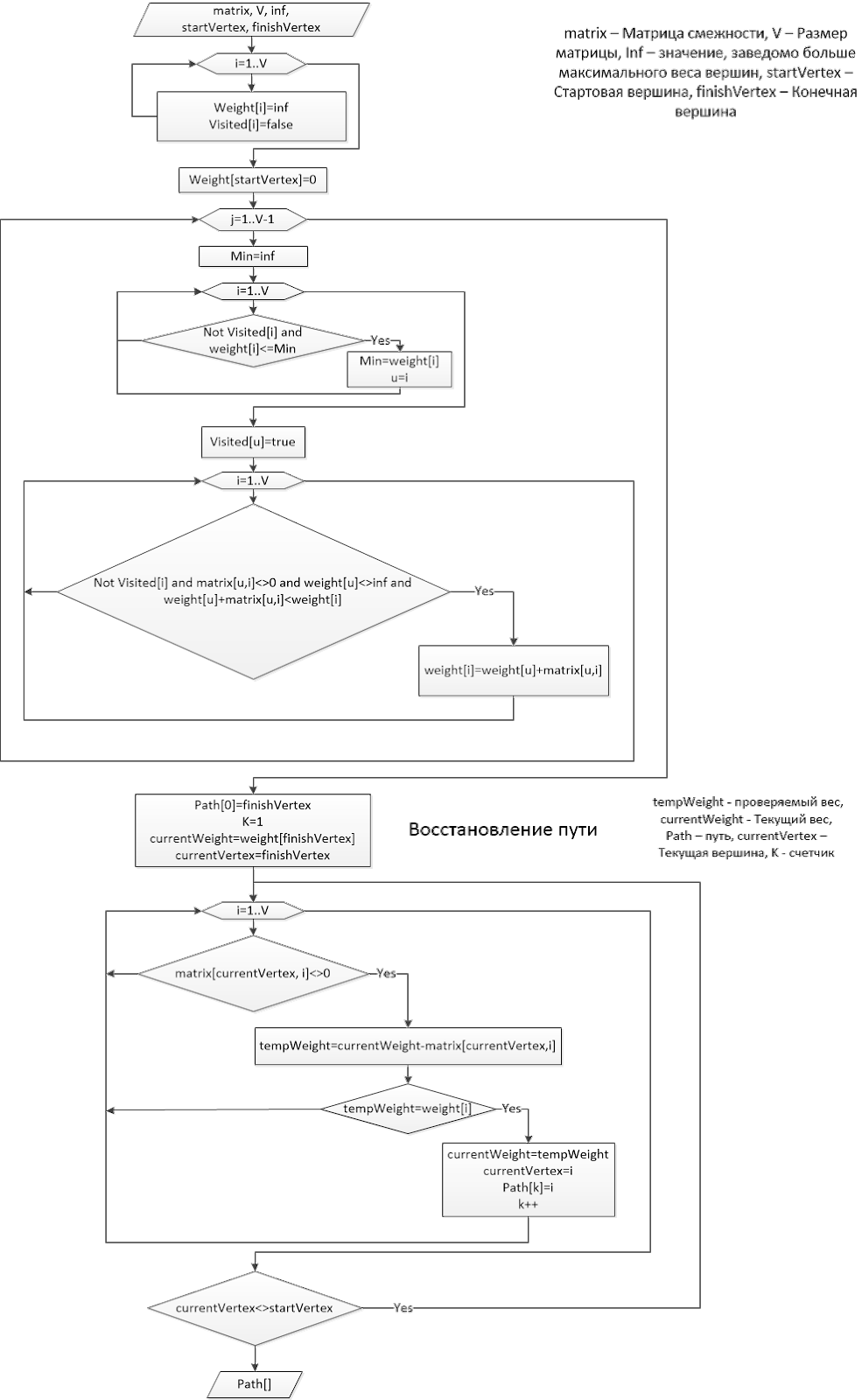
Según el algoritmo, y mejor según su modelo matemático, ya podemos crear un programa para el robot. La entrada será la matriz de adyacencia, los puntos inicial y final. Después de todas las acciones descritas, la búsqueda de la ruta más corta entre cualquier punto en el mismo mapa se puede encontrar rápidamente.
Por supuesto, además del algoritmo Dijkstra, nuestro robot basado en LEGO EV3 necesitará una serie de módulos de programa (subprogramas) más simples: moverse a lo largo de la línea hasta la intersección, contar las intersecciones, girar en ambas direcciones, determinar su ubicación en relación con el sistema de coordenadas absoluto X, Y, where, donde X, Y - coordenadas en la cuadrícula, Θ - dirección actual del robot (expresada a través del código, por ejemplo 1 - arriba, 2 - a la derecha, 3 - abajo, 4 - a la izquierda).
Y aquí hay una demostración en vivo de la solución al problema. Los datos de entrada son ligeramente diferentes, pero esto no cambia la esencia.Tema de bonificación: odometría
Las capacidades de odometría se pueden integrar en tareas para moverse en el suelo, por ejemplo, para que el robot en el laberinto comprenda dónde está y hacia dónde se mueve. Usando odometría, el movimiento del robot se estima en base a datos sobre el movimiento de los accionamientos (rotación de los motores). Conociendo el diámetro de las ruedas, podemos calcular la distancia que recorrió el robot en un tiempo determinado. Conociendo la velocidad angular de las ruedas, podemos determinar el ángulo por el cual el robot giró en relación con el original. Y al establecer diferentes velocidades angulares, podemos ajustar el movimiento del robot a lo largo del arco y al mismo tiempo determinar los "bucles" al mover el robot, como en el siguiente video:
En las escuelas, se presta mucha atención a la trigonometría, pero su aplicación práctica no está cubierta de ninguna manera. Los problemas de odometría resueltos con LEGO EV3 muestran por qué puede ser necesaria la trigonometría. En la práctica, la odometría se usa no solo en el transporte, sino también, por ejemplo, para rastrear la posición de una herramienta en máquinas CNC (control numérico).
¿Dónde puedo aprender todo esto?
Me permito un poco de publicidad. La tarea descrita anteriormente, y las tareas más complejas, bien pueden ser resueltas por niños de 7 ° a 9 ° grado que han sido entrenados en clubes de robótica. Dirijo uno de esos clubes, Robit, en Ekaterimburgo; este es nuestro
programa de entrenamiento . Filmamos el video de la demostración para la tarea anterior en una de las clases. Luego, un alumno de octavo grado de nuestro club en 6 horas estudió los conceptos básicos de la teoría de grafos y resolvió un problema similar.
Cómo elegir un entorno de programación LEGO EV3
La resolución de problemas es imposible sin elegir el entorno de programación adecuado para LEGO EV3. Hay
material separado sobre lo último en esta área. Intento enseñar a los niños a elegir un lenguaje de programación para la tarea, y no una tarea para ese lenguaje de programación, cuya sintaxis aprendieron. Pero en los grados inferiores es difícil trabajar de inmediato en un lenguaje de programación basado en texto, por lo que comenzamos a estudiar algoritmos en lenguajes gráficos, donde el umbral de entrada es más bajo. A partir de los 10 años, los estudiantes aprenden el entorno gráfico de EV3 Mindstorms. Algunas competiciones de robótica restringen los juegos de herramientas solo a este entorno.
A partir de los 12 años, los chicos comienzan a dominar el entorno EV3 Basic. El entorno es relativamente fácil de aprender, y Basic ofrece una potente funcionalidad para la plataforma LEGO EV3. Además, programamos en el entorno EV3Dev, donde puede instalar muchos idiomas diferentes: Python, Java, C. Con EV3Dev, los chicos obtienen su primera experiencia en idiomas populares y populares. El único inconveniente de EV3Dev es una tasa de sondeo del sensor relativamente más baja en comparación con otros entornos. Con el enfoque correcto, LEGO EV3 se convierte en una gran herramienta para conocer la programación. Cuando los estudiantes ven su código dando vida a un constructor, esta es una excelente motivación.
Que sigue
Después de estudiar tales algoritmos en la escuela secundaria, los niños podrán consolidar aún más sus conocimientos y, por ejemplo, participar en el diseño y asignaturas de las Olimpiadas que otorgan bonificaciones reales, por ejemplo, 100 puntos automáticamente en el examen al ingresar a las universidades.