Sobre la solvencia de los problemas de circunvalación en tiempo polinómico

Los estudiantes llegan a conocer el problema de la circunvalación al tomar cursos de bioinformática, en particular, uno de los más altos y de espíritu más cercano para los programadores es el curso de Bioinformática (Pavel Pevzner) en el curso de la Universidad de California en San Diego. El problema llama la atención por la simplicidad del enunciado, la importancia práctica y por el hecho de que todavía se considera no resuelto con la aparente capacidad de resolverlo con una codificación simple. El problema se plantea de esta manera. ¿Es posible restaurar las coordenadas de muchos puntos en el tiempo polinómico?$$ $ en línea $ X $ en línea $ si se conoce el conjunto de todas las distancias por pares entre ellos$$ $ en línea $ \ Delta X $ en línea $ ?

Esta tarea aparentemente simple todavía está en la lista de problemas no resueltos de geometría computacional. Además, la situación ni siquiera concierne a puntos en espacios multidimensionales, especialmente los curvos, el problema ya es la opción más simple, cuando todos los puntos tienen coordenadas enteras y están localizados en la misma línea.

En el último medio siglo, desde que los matemáticos reconocieron esta tarea como un desafío (Shamos, 1975), se obtuvieron algunos resultados. Consideramos dos casos posibles para un problema unidimensional:

1. los puntos se encuentran en línea recta (problema con la autopista de peaje)
2. los puntos están ubicados en un círculo (problema de circunvalación)

Estos dos casos recibieron nombres diferentes por una razón: se requieren diferentes esfuerzos para resolverlos. De hecho, la primera tarea se resolvió lo suficientemente rápido (en 15 años) y se construyó un algoritmo de retroceso, que restaura la solución en promedio en tiempo cuadrático$$ $ en línea $ O (n ^ 2 \ log n) $ en línea $ donde$$ $ en línea $ n $ en línea $ - el número de puntos (Skiena, 1990); para la segunda tarea, esto no se ha hecho hasta ahora, y el algoritmo mejor propuesto tiene una complejidad computacional exponencial$$ $ en línea $ O (n ^ n \ log n) $ en línea $ (Lemke, 2003). La imagen a continuación muestra una estimación de cuánto tiempo trabajará su computadora para obtener una solución para un conjunto con un número diferente de puntos.



Es decir, en un tiempo psicológicamente aceptable (~ 10 segundos), puede restaurar muchos$$ $ en línea $ X $ en línea $ hasta 10 mil puntos en un caso de autopista de peaje y solo ~ 10 puntos para un caso de circunvalación, lo que no tiene ningún valor para aplicaciones prácticas.

Un poco de aclaracion. Se cree que el problema de la autopista de peaje se resuelve en términos de uso práctico, es decir, para la gran mayoría de los datos encontrados. En este caso, las objeciones de los matemáticos puros al hecho de que hay conjuntos de datos especiales para los cuales se ignora el tiempo para obtener una solución exponencialmente$$ $ en línea $ O (2 ^ n \ log n) $ en línea $ (Zhang, 1982). A diferencia de la autopista de peaje, el problema de la circunvalación con su algoritmo exponencial no puede considerarse resuelto de ninguna manera.

Importancia de resolver problemas de circunvalación en términos de bioinformática

A finales del siglo XX, se descubrió una nueva vía para la síntesis de biomoléculas, llamada vía de síntesis no ribosómica. Su principal diferencia con la ruta de síntesis clásica es que el resultado final de la síntesis no está codificado en el ADN en absoluto. En cambio, solo el código de "herramientas" (muchas sintetasas diferentes) que pueden recolectar estos objetos está escrito en el ADN. Por lo tanto, la ingeniería de biomáquina se enriquece significativamente, y en lugar de un solo tipo de colector (ribosoma), que funciona con solo 20 partes estándar (aminoácidos estándar, también llamados proteinógenos), aparecen muchos otros tipos de colectores que pueden funcionar con más de 500 partes estándar y no estándar. (aminoácidos no proteinógenos y sus diversas modificaciones). Y estos ensambladores no solo pueden conectar partes en cadenas, sino que también obtienen estructuras muy complejas: cíclicas, ramificadas, así como estructuras con muchos ciclos y ramificaciones. Todo esto aumenta significativamente el arsenal de la célula para varios casos de su vida. La actividad biológica de tales estructuras es alta, la especificidad (selectividad de acción), también, una variedad de propiedades no está limitada. La clase de estos productos celulares en la literatura inglesa se llama NRP (productos no ribosómicos o péptidos no ribosómicos). Los biólogos esperan que sea precisamente entre tales productos del metabolismo celular que se puedan encontrar nuevas preparaciones farmacológicas que sean altamente efectivas y que no tengan efectos secundarios debido a la especificidad.

La única pregunta es, ¿cómo y dónde buscar NRP? Son muy efectivos, por lo tanto, la célula no tiene absolutamente ninguna necesidad de producirlos en grandes cantidades, y sus concentraciones son insignificantes. Por lo tanto, los métodos de extracción química con su baja precisión de ~ 1% y los enormes costos de reactivos y tiempo son inútiles. Siguiente No están codificados en el ADN, lo que significa que todas las bases de datos que se acumularon durante la decodificación del genoma, y ​​todos los métodos de bioinformática y genómica, también son inútiles. La única forma de encontrar algo es a través de métodos físicos, a saber, la espectroscopía de masas. Además, el nivel de detección de la materia en los espectrómetros modernos es tan alto que le permite encontrar cantidades insignificantes, un total> ~ 800 moléculas (rango atomolar o concentración$$ $ en línea $ 10 ^ {- 18} $ en línea $ )

"

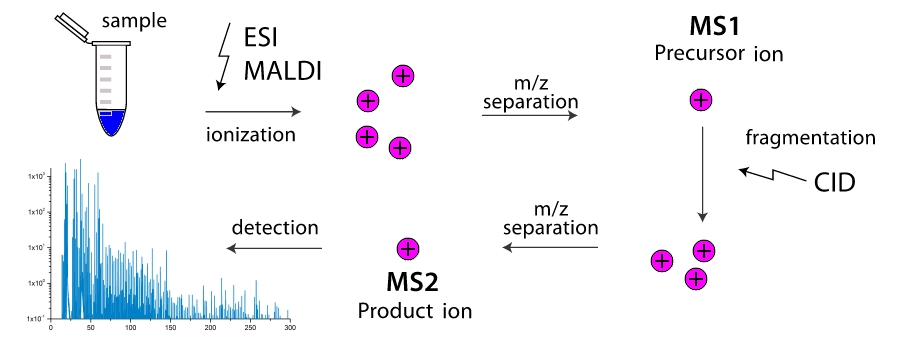
¿Cómo funciona un espectrómetro de masas? En la cámara de trabajo del dispositivo, las moléculas se descomponen en fragmentos (más a menudo a través de sus colisiones entre sí, con menos frecuencia debido a influencias externas). Estos fragmentos son ionizados y luego acelerados y separados en un campo electromagnético externo. La separación se produce cuando el detector alcanza o por el ángulo de giro en el campo magnético, porque la masa del fragmento es mayor y su carga es menor, cuanto más torpe sea. Así, el espectrómetro de masas "pesa" las masas de fragmentos. Además, el "pesaje" se puede hacer por etapas, filtrando repetidamente fragmentos con la misma masa (más precisamente, con un valor$$ $ en línea $ m / z $ en línea $ ) y llevarlos a través de la fragmentación con mayor separación. Los espectrómetros de masas de dos etapas están ampliamente distribuidos y se denominan espectrómetros de masas en tándem, los espectrómetros de masas de etapas múltiples son extremadamente raros y simplemente se designan como$$ $ en línea $ ms ^ n $ en línea $ donde$$ $ en línea $ n $ en línea $ - El número de etapas. Y aquí aparece la tarea, ¿cómo, conociendo solo las masas de todo tipo de fragmentos de cualquier molécula, conocer su estructura? Entonces llegamos a problemas de autopista y circunvalación, para péptidos lineales y cíclicos, respectivamente.

Explicaré con más detalle cómo la tarea de restaurar la estructura de una biomolécula se reduce a los problemas indicados utilizando el ejemplo de un péptido cíclico.



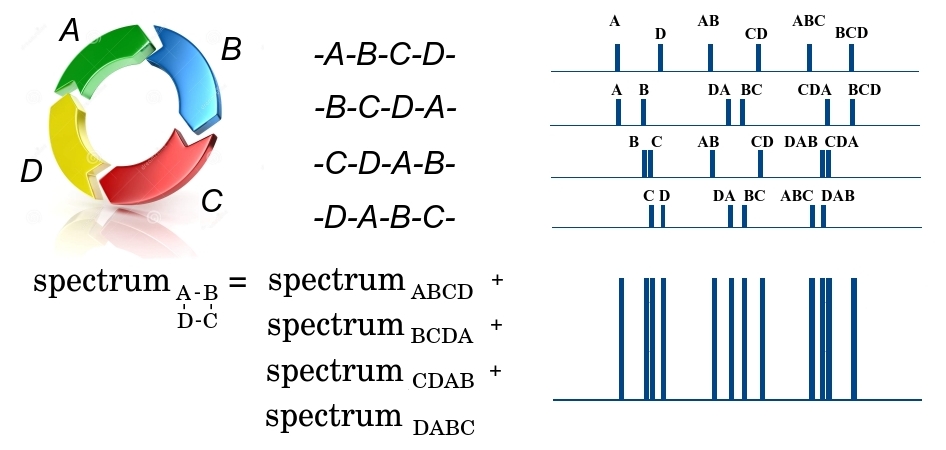
El péptido cíclico ABCD en la primera etapa de fragmentación puede romperse en 4 lugares, ya sea por enlace DA, o por AB, BC o CD, formando 4 péptidos lineales posibles, ya sea ABCD, BCDA, CDAB o DABC. Dado que una gran cantidad de péptidos idénticos pasan a través del espectrómetro, tendremos fragmentos de los 4 tipos en la salida. Además, observamos que todos los fragmentos tienen la misma masa y no se pueden separar en la primera etapa. En la segunda etapa, el fragmento lineal ABCD se puede romper en tres lugares, formando fragmentos más pequeños con diferentes masas A y BCD, AB y CD, ABC y D, y formando el espectro de masas correspondiente. En este espectro, la masa del fragmento se representa a lo largo del eje xy el número de fragmentos pequeños con una masa dada a lo largo del eje y. Del mismo modo, se forman espectros para los tres fragmentos lineales restantes de BCDA, CDAB y DABC. Como los 4 fragmentos grandes pasaron a la segunda etapa, se suman todos sus espectros. Total, el resultado es algo masivo$$ $ en línea $ \ {m_1 ^ {n_1}, m_2 ^ {n_2}, .., m_q ^ {n_q} \} $ en línea $ donde$$ $ en línea $ m_i $ en línea $ - algo de masa, y$$ $ en línea $ n_i $ en línea $ - la frecuencia de su repetición. Al mismo tiempo, no sabemos a qué fragmento pertenece esta masa y si este fragmento es único, ya que diferentes fragmentos pueden tener una masa. Cuanto más alejados están los enlaces en el péptido, mayor es la masa del fragmento de péptido entre ellos. Es decir, la tarea de restaurar el orden de los elementos en un péptido cíclico se reduce a un problema de circunvalación, en el que los elementos del conjunto$$ $ en línea $ X $ en línea $ son enlaces en el péptido y elementos de una multitud$$ $ en línea $ \ Delta X $ en línea $ - masas de fragmentos entre enlaces.

Anticipación de la existencia de un algoritmo con tiempo polinómico para resolver problemas de circunvalación

Por mi experiencia y por comunicarme con personas que intentaron o realmente hicieron algo para resolver este problema, noté que la gran mayoría de las personas trata de resolverlo en el caso general o para datos enteros en un rango estrecho, como este (1, 50) Ambas opciones están condenadas al fracaso. Para el caso general, se demostró que el número total de soluciones para problemas de circunvalación en el caso unidimensional$$ $ en línea $ S_1 (n) $ en línea $ limitado por valores (Lemke, 2003)

$$$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o (1)}} \ leq S_1 (n) \ leq \ frac {1} {2} n ^ {n-2} $$ display $$

lo que significa la presencia de un número exponencial de soluciones en los asintóticos$$ $ en línea $ n \ rightarrow \ infty $ en línea $ . Obviamente, si el número de soluciones crece exponencialmente, entonces el tiempo de su recepción no puede crecer más lentamente. Es decir, para el caso general, es imposible obtener una solución de tiempo polinomial. En cuanto a los datos enteros en un rango estrecho, todo se puede verificar experimentalmente, ya que no es demasiado difícil escribir código que busque una solución mediante una búsqueda exhaustiva. Para pequeños$$ $ en línea $ n $ en línea $ dicho código no llevará mucho tiempo. Los resultados de la prueba de dicho código mostrarán que, bajo tales condiciones de datos, el número total de soluciones diferentes para cualquier conjunto$$ $ en línea $ \ Delta X $ en línea $ ya en pequeño$$ $ en línea $ n $ en línea $ También crece extremadamente bruscamente.

Después de conocer estos hechos, puede aguantar y renunciar a esta tarea. Admito que esta es una de las razones por las cuales el problema de la circunvalación todavía se considera sin resolver. Sin embargo, existen lagunas. Recordemos que la función exponencial$$ $ en línea $ e ^ {\ alpha x} $ en línea $ Se comporta muy interesante. Al principio, crece terriblemente lento, aumentando de 0 a 1 en un intervalo infinitamente grande desde$$ $ en línea $ \ infty $ en línea $ a 0, entonces su crecimiento se acelera cada vez más. Sin embargo, cuanto menor sea el valor$$ $ en línea $ \ alpha $ en línea $ cuanto mayor sea el valor$$ $ en línea $ x $ en línea $ para que el resultado de la función supere algún valor establecido$$ $ en línea $ y = \ xi $ en línea $ . Como tal valor, es conveniente elegir un número$$ $ en línea $ \ xi = 2 $ en línea $ , ante él la única solución, después de él hay muchas decisiones. Pregunta ¿Y alguien verificó la dependencia del número de decisiones sobre qué datos llegan a la entrada? Sí lo hice Hay una maravillosa disertación de doctorado por la matemática croata Tamara Dakis (Dakic, 2000), en la que determinó qué condiciones deben cumplir los datos de entrada para que el problema se resuelva en tiempo polinómico. Los más importantes son la singularidad de la solución y la ausencia de duplicación en el conjunto de datos de entrada.$$ $ en línea $ \ Delta X $ en línea $ . El nivel de su tesis doctoral es muy alto. Es desafortunado que esta estudiante se haya limitado solo a un problema de la autopista de peaje, estoy convencido de que si hubiera vuelto su interés en el problema de la circunvalación, eso se habría resuelto por mucho tiempo.

Obtención de un algoritmo con tiempo polinómico para resolver problemas de circunvalación

Fue posible encontrar los datos para los cuales es posible construir el algoritmo deseado por casualidad. Tomó ideas adicionales. La idea principal surgió de la observación (véase más arriba) de que el espectro de un péptido cíclico es la suma de los espectros de todos los péptidos lineales que se forman en roturas de anillo individuales. Dado que la secuencia de aminoácidos en un péptido puede restaurarse a partir de cualquier péptido lineal de este tipo, el número total de líneas en el espectro es significativo (en$$ $ en línea $ n $ en línea $ tiempos donde$$ $ en línea $ n $ en línea $ - el número de aminoácidos en el péptido) es excesivo. La pregunta es solo qué líneas deben excluirse del espectro para no perder la capacidad de restaurar la secuencia. Dado que ambas tareas (restauración de la secuencia de péptidos cíclicos del espectro de masas y el problema de la circunvalación) son matemáticamente isomórficas, también es posible diluir muchas$$ $ en línea $ \ Delta X $ en línea $ .

Operaciones de adelgazamiento$$ $ en línea $ \ Delta X $ en línea $ fueron construidos usando simetrías locales del conjunto$$ $ en línea $ \ Delta X $ en línea $ (Fomin, 2016a).

• Simetrización La primera operación es seleccionar un elemento arbitrario del conjunto$$ $ en línea $ x _ {\ mu} \ in \ Delta X $ en línea $ y eliminar de$$ $ en línea $ \ Delta X $ en línea $ todos los elementos excepto aquellos que tienen pares simétricos con respecto a puntos$$ $ en línea $ x _ {\ mu} / 2 $ en línea $ y$$ $ en línea $ (L + x _ {\ mu}) / 2 $ en línea $ donde$$ $ en línea $ L $ en línea $ - circunferencia (recuerdo que en el caso de la circunvalación, todos los puntos se encuentran en el círculo).
• Solución parcial convolución. La segunda operación utiliza las conjeturas sobre la solución, es decir, el conocimiento de los puntos individuales que pertenecen a la solución, la llamada solución parcial. De muchos$$ $ en línea $ \ Delta X $ en línea $ todos los elementos también se eliminan, excepto aquellos que satisfacen la condición: si medimos la distancia desde el punto que se prueba a todos los puntos de una solución parcial, entonces todos los valores obtenidos están en$$ $ en línea $ \ Delta X $ en línea $ . Aclararé que si al menos una de las distancias obtenidas está ausente en$$ $ en línea $ \ Delta X $ en línea $ entonces el punto es ignorado.

Los teoremas demostraron que ambas operaciones debilitan el conjunto$$ $ en línea $ \ Delta X $ en línea $ , pero aún le quedan elementos suficientes para restaurar la solución$$ $ en línea $ X $ en línea $ . Usando estas operaciones, se construyó e implementó un algoritmo en c ++ para resolver el problema de circunvalación (Fomin, 2016b). El algoritmo difiere poco del algoritmo de retroceso clásico (es decir, tratamos de construir una solución enumerando las posibles opciones y regresamos si obtenemos un error durante la construcción). La única diferencia es que para reducir el conjunto$$ $ en línea $ \ Delta X $ en línea $ probarnos se vuelve significativamente menos opciones.

Aquí hay un ejemplo de cuántos$$ $ en línea $ \ Delta X $ en línea $ al adelgazar



Se realizaron experimentos computacionales para péptidos cíclicos de longitud generados aleatoriamente$$ $ en línea $ n $ en línea $ de 10 a 1000 aminoácidos (el eje de ordenadas en una escala logarítmica). La abscisa también muestra en una escala logarítmica el número de elementos en los conjuntos adelgazados por varias operaciones.$$ $ en línea $ \ Delta X $ en línea $ en unidades$$ $ en línea $ n $ en línea $ . Tal representación es absolutamente inusual, por lo tanto, descifraré cómo se lee en un ejemplo. Nos fijamos en el diagrama de la izquierda. Deje que el péptido tenga una longitud$$ $ en línea $ n = 100 $ en línea $ . Para él, la cantidad de elementos en el conjunto$$ $ en línea $ \ Delta X $ en línea $ es igual$$ $ en línea $ n ^ 2 = 10000 $ en línea $ (este es un punto en la línea discontinua superior$$ $ en línea $ y = n ^ 2 $ en línea $ ) Después de sacar del set$$ $ en línea $ \ Delta X $ en línea $ elementos repetidos, número de elementos en$$ $ en línea $ \ Delta X $ en línea $ disminuye a$$ $ en línea $ n_D \ aprox n ^ {1.9} \ aproximadamente 6300 $ en línea $ (círculos con cruces). Después de la simetrización, el número de elementos cae a$$ $ en línea $ n_S \ aprox n ^ {1.75} \ aprox 3100 $ en línea $ (círculos negros), y después de convolución por solución parcial a$$ $ en línea $ n_C \ aprox n ^ {1.35} \ aproximadamente 500 $ en línea $ (cruces) Total, el volumen total del conjunto$$ $ en línea $ \ Delta X $ en línea $ reducido solo 20 veces. Para un péptido de la misma longitud, pero en el diagrama de la derecha, la contracción proviene de$$ $ en línea $ n ^ 2 = 10000 $ en línea $ antes$$ $ en línea $ N_C \ aprox n \ aprox 100 $ en línea $ Es decir, 100 veces.

Tenga en cuenta que la generación de casos de prueba para el diagrama de la izquierda se realiza de modo que el nivel de duplicación$$ $ en línea $ k_ {dup} $ en línea $ en$$ $ en línea $ \ Delta X $ en línea $ estaba en el rango de 0.1 a 0.3, y para la derecha, menos de 0.1. El nivel de duplicación se define como$$ $ en línea $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ en línea $ donde$$ $ en línea $ N_u $ en línea $ - el número de elementos únicos en el conjunto$$ $ en línea $ \ Delta X $ en línea $ . Tal definición da un resultado natural: en ausencia de duplicados en el conjunto$$ $ en línea $ \ Delta X $ en línea $ su poder es igual$$ $ en línea $ N_u = n ^ 2 $ en línea $ y$$ $ en línea $ k_ {dup} = 0 $ en línea $ en la duplicación máxima posible$$ $ en línea $ N_u = n $ en línea $ y$$ $ en línea $ k_ {dup} = 1 $ en línea $ . Cómo hacer posible proporcionar un nivel diferente de duplicación, diré un poco más adelante. Los diagramas muestran que cuanto más bajo es el nivel de duplicación, más delgado es$$ $ en línea $ \ Delta X $ en línea $ a las$$ $ en línea $ k_ {dup} <0.1 $ en línea $ número de elementos en adelgazado$$ $ en línea $ \ Delta X $ en línea $ generalmente alcanza su límite$$ $ en línea $ O (n ^ 2) \ rightarrow O (n) $ en línea $ , ya que en el conjunto diezmado es menor que$$ $ en línea $ O (n) $ en línea $ no se pueden obtener elementos (las operaciones almacenan suficientes elementos para obtener una solución en la que$$ $ en línea $ n $ en línea $ elementos). El hecho de reducir el poder del conjunto$$ $ en línea $ \ Delta X $ en línea $ para el límite inferior es muy importante, es él quien conduce a cambios dramáticos en la complejidad computacional de obtener una solución.

Después de insertar operaciones de adelgazamiento en el algoritmo de retroceso y de resolver el problema de la circunvalación, se reveló un análogo completo de lo que habló Tamara Dakis con respecto al problema de la autopista de peaje. Déjame recordarte. Ella dijo que para problemas de autopista de peaje es posible obtener una solución en tiempo polinómico si la solución es única y no hay duplicación en$$ $ en línea $ \ Delta X $ en línea $ . Resultó que no es necesaria una completa ausencia de duplicación (apenas es posible para datos reales), es suficiente que su nivel sea bastante pequeño. La figura a continuación muestra cuánto tiempo se requiere para obtener una solución del problema de la circunvalación dependiendo de la longitud del péptido y el nivel de duplicación en$$ $ en línea $ \ Delta X $ en línea $ .



En la figura, tanto la abscisa como la ordenada se dan en una escala logarítmica. Esto le permite ver claramente si la dependencia del tiempo de conteo con la longitud de la secuencia$$ $ en línea $ T = f (n) $ en línea $ exponencial (línea recta) o polinomio (curva de forma logarítmica). Como se puede ver en los diagramas, con un bajo nivel de duplicación (diagrama de la derecha), la solución se obtiene en tiempo polinómico. Bueno, para ser más precisos, la solución se obtiene en tiempo cuadrático. Esto ocurre cuando las operaciones de adelgazamiento reducen la potencia del conjunto a un límite inferior.$$ $ en línea $ O (n ^ 2) \ rightarrow O (n) $ en línea $ , quedan pocos puntos, regresa cuando las opciones de enumeración se vuelven únicas, y en esencia el algoritmo deja de iterar sobre las opciones, pero simplemente construye una solución a partir de lo que queda.

PD: Bueno, revelaré el último secreto con respecto a la generación de sets en diferentes niveles de duplicación. Esto se debe a la precisión diferente de la presentación de datos. Si los datos se generan con baja precisión (por ejemplo, redondeando a enteros), entonces el nivel de duplicación se vuelve alto, más de 0.3.Si los datos se generan con buena precisión, por ejemplo, hasta 3 decimales, entonces el nivel de duplicación disminuye bruscamente, menos de 0.1. Y de aquí sigue el último comentario más importante.

Para datos reales, en condiciones de precisión cada vez mayor de las mediciones, el problema de la circunvalación se resuelve en tiempo real.


Literatura

1. Dakic, T. (2000). Sobre el problema de la autopista de peaje. Tesis doctoral, Universidad Simon Fraser.
2. Fomin. E. (2016a) Un enfoque simple para la reconstrucción de un conjunto de puntos del conjunto múltiple de n ^ 2 distancias por pares en n ^ 2 pasos para el problema de secuenciación: I. Teoría. J Comput Biol. 2016, 23 (9): 769-75.
3. Fomin. E. (2016b) Un enfoque simple para la reconstrucción de un conjunto de puntos del conjunto múltiple de n ^ 2 distancias por pares en n ^ 2 pasos para el problema de secuenciación: II. Algoritmo J Comput Biol. 2016, 23 (12): 934-942.
4. Lemke, P., Skiena, S. y Smith, W. (2003). Reconstrucción de conjuntos a partir de distancias entre puntos. Algoritmos de geometría discreta y computacional y combinatoria, 25: 597–631.
5. Skiena, S., Smith, W. y Lemke, P. (1990). Reconstrucción de conjuntos a partir de distancias entre puntos. En Actas del Sexto Simposio ACM sobre Geometría Computacional, páginas 332–339. Berkeley, CA
6. Zhang, Z. 1982. Un ejemplo exponencial para un algoritmo de mapeo de resumen parcial. J. Comp. Biol. 1, 235–240.