Implementación del algoritmo k-means (k-means) usando el ejemplo de trabajar con píxeles

Hola a todos! Recientemente, fue necesario escribir código para implementar la segmentación de imágenes usando el método k-means (inglés k-means). Bueno, lo primero que hace Google es ayudar. Encontré mucha información, como desde un punto de vista matemático (todo tipo de garabatos matemáticos complejos allí, comprenderá qué demonios está escrito allí), así como algunas implementaciones de software que están en Internet en inglés. Estos códigos son ciertamente hermosos, sin duda, pero la esencia de la idea es difícil de entender. De alguna manera, todo es complicado allí, confuso, y sin embargo, a mano, a mano, no escribirás el código, no entenderás nada. En este artículo quiero mostrar una implementación simple, no productiva, pero espero que sea comprensible de este maravilloso algoritmo. Ok, vamos!

Entonces, ¿qué es la agrupación en términos de nuestras percepciones? Déjame darte un ejemplo, digamos que hay una bonita foto con flores de la cabaña de tu abuela.



La pregunta es: para determinar cuántas áreas en esta foto se rellenan con aproximadamente el mismo color. Bueno, no es para nada difícil: pétalos blancos, uno, centros amarillos, dos (no soy biólogo, no sé cómo se llaman), tres verdes. Estas secciones se llaman grupos. Un clúster es una combinación de datos que tienen características comunes (color, posición, etc.). El proceso de determinar y colocar cada componente de cualquier dato en dichos grupos - secciones se denomina agrupamiento.

Hay muchos algoritmos de agrupamiento, pero el más simple de ellos es k - medio, que se discutirá más adelante. K-means es un algoritmo simple y eficiente que es fácil de implementar utilizando un método de software. Los datos que distribuiremos en grupos son píxeles. Como sabes, un píxel de color tiene tres componentes: rojo, verde y azul. La imposición de estos componentes y crea una paleta de colores existentes.



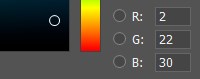
En la memoria de la computadora, cada componente de color se caracteriza por un número de 0 a 255. Es decir, combinando diferentes valores de rojo, verde y azul, obtenemos una paleta de colores en la pantalla.

Usando píxeles como ejemplo, implementamos nuestro algoritmo. K-means es un algoritmo iterativo, es decir, dará el resultado correcto, después de un cierto número de repeticiones de algunos cálculos matemáticos.

Algoritmo

1. Debe saber de antemano cuántos clústeres necesita para distribuir los datos. Esta es una desventaja significativa de este método, pero este problema se resuelve con implementaciones mejoradas del algoritmo, pero esto, como dicen, es una historia completamente diferente.
2. Necesitamos elegir los centros iniciales de nuestros grupos. Como? Si al azar. Por qué Para que pueda ajustar cada píxel al centro del clúster. El centro es como el Rey, alrededor del cual se reúnen sus sujetos: píxeles. Es la "distancia" desde el centro al píxel lo que determina a quién obedecerá cada píxel.
3. Calculamos la distancia desde cada centro a cada píxel. Esta distancia se considera como la distancia euclidiana entre puntos en el espacio y, en nuestro caso, como la distancia entre los tres componentes de color:

   $$$$ display $$ \ sqrt {(R_ {2} -R_ {1}) ^ 2 + (G_ {2} -G_ {1}) ^ 2 + (B_ {2} -B_ {1}) ^ 2} . $$ display $$

   Calculamos la distancia desde el primer píxel a cada centro y determinamos la distancia más pequeña entre este píxel y los centros. Para el centro, la distancia a la cual es el más pequeño, recalculamos las coordenadas como la media aritmética entre cada componente del píxel, el rey y el píxel, el sujeto. Nuestro centro cambia en el espacio según los cálculos.
4. Después de contar todos los centros, distribuimos los píxeles en grupos, comparando la distancia de cada píxel a los centros. Un píxel se coloca en un grupo, al centro del cual está más cerca que a los otros centros.
5. Todo comienza de nuevo, siempre y cuando los píxeles permanezcan en los mismos grupos. A menudo esto puede no suceder, ya que con una gran cantidad de datos los centros se moverán en un radio pequeño, y los píxeles a lo largo de los bordes de los grupos saltarán a uno u otro grupo. Para hacer esto, determine el número máximo de iteraciones.

Implementación

Implementaré este proyecto en C ++. El primer archivo es "k_means.h", en el que definí los principales tipos de datos, constantes y la clase principal para trabajar: "K_means".
Para caracterizar cada píxel, cree una estructura que consta de tres componentes de píxel, para los cuales elegí el tipo doble para cálculos más precisos, y también definí algunas constantes para que el programa funcione:

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_means clase en sí:

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

Repasemos los componentes de la clase:

vectorpixcel: un vector para píxeles;
q_klaster - número de clusters;
k_pixcel - número de píxeles;
vectorcentr - un vector para centros de agrupamiento, el número de elementos en él está determinado por q_klaster;
Identificar_centros (): un método para seleccionar aleatoriamente los centros iniciales entre los píxeles de entrada;
compute () y compute_s () son métodos integrados para calcular la distancia entre píxeles y centros de recálculo, respectivamente;
tres constructores: el primero es por defecto, el segundo es para inicializar píxeles desde una matriz, el tercero es para inicializar píxeles desde un archivo de texto (en mi implementación, el archivo se llena accidentalmente con datos al principio, y luego los píxeles se leen desde este archivo para que el programa funcione, ¿por qué no directamente en el vector? solo es necesario en mi caso);
agrupamiento (std :: ostream & os) - método de agrupamiento;
método y sobrecarga de la declaración de salida para publicar los resultados.

Implementación del método:

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

Este es un método para seleccionar los centros de agrupación iniciales y agregarlos al vector del centro. Se realiza una verificación para repetir centros y reemplazarlos en estos casos.

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

Una implementación de constructor para inicializar píxeles desde una matriz.

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

Pasamos un objeto de entrada a este constructor para poder ingresar datos tanto del archivo como de la consola.

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

El principal método de agrupamiento.

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

La salida de los datos iniciales.

Ejemplo de salida

Este ejemplo está planeado con anticipación, los píxeles se seleccionan específicamente para demostración. Dos iteraciones son suficientes para que el programa agrupe los datos en tres grupos. Mirando los centros de las dos últimas iteraciones, puede ver que prácticamente permanecieron en su lugar.

Más interesantes son los casos de píxeles generados aleatoriamente. Habiendo generado 50 puntos que deben dividirse en 10 grupos, obtuve 5 iteraciones. Habiendo generado 50 puntos que deben dividirse en 3 grupos, obtuve las 100 iteraciones máximas permitidas. Puede notar que cuantos más grupos, más fácil es para el programa encontrar los píxeles más similares y combinarlos en grupos más pequeños, y viceversa: si hay pocos grupos y hay muchos puntos, el algoritmo a menudo termina solo cuando se excede el número máximo de iteraciones, ya que algunos píxeles saltan constantemente de un grupo a otro. Sin embargo, la mayor parte aún se determina en sus grupos por completo.

Bueno, ahora verifiquemos el resultado de la agrupación. Tomando el resultado de algunos grupos del ejemplo de 50 puntos por cada 10 grupos, conduje el resultado de estos datos a Illustrator y esto es lo que sucedió:



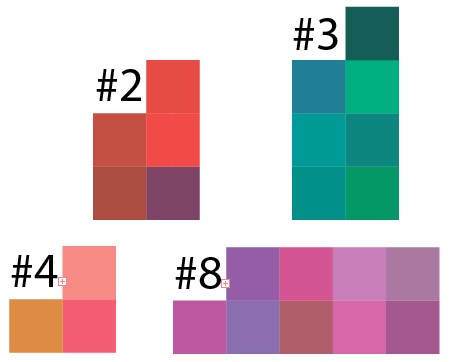
Se puede ver que en cada grupo prevalece cualquier tono de color, y aquí debe comprender que los píxeles se seleccionaron al azar, el análogo de dicha imagen en la vida real es algún tipo de imagen sobre la que se rociaron accidentalmente todos los colores y es difícil seleccionar áreas de colores similares.

Digamos que tenemos una foto así. Podemos definir una isla como un grupo, pero con un aumento vemos que consiste en diferentes tonos de verde.



Y este es el clúster 8, pero en una versión más pequeña, el resultado es similar:



La versión completa del programa se puede ver en mi GitHub .