Matemáticas entretenidas. El sistema de numeración más económico.

Todos sabemos por el curso escolar cuál es el sistema de números (SS). Pero no todos piensan en cuánto cuestan las SS. Es decir qué conjunto de números necesitamos para representar el número en este SS. Cuando tenemos un conjunto limitado de elementos únicos (piedras multicolores de diferentes tamaños) con los que podemos representar un número, ¿cuál es el número máximo que podemos representar con estos elementos? (todas las piedras rojas son cero, las verdes son una, las azules son dos, etc., las pequeñas son cero, las medianas son las primeras, las grandes son las segundas, etc.). ¿Dónde está la línea en la que la base del SS juega un papel más importante que la capacidad de dígitos del número?

Tomemos por ejemplo n - el número de elementos igual a 60. Habiendo dividido los elementos en 2 grupos (sistema de números binarios) obtenemos 30 dígitos. 30 unidades es el número más grande de 30 bits con una base de 2. Si le suma 1, obtendrá una unidad con 30 ceros, es decir 2 en el 30, ya que cada cero es una potencia de dos, y los dígitos comienzan en 0, y no se olvide de restar la unidad que se agregó.

Para otros SS, de manera similar $$$y = x ^ {60 / x} -1$donde y es el número máximo, x es la base del grado.

Puntos de construcción:

$$$2 ^ {30} -1 = 1 \, 073 \, 741 \, 823$.
$$$3 ^ {20} -1 = 3 \, 486 \, 784 \, 400$.
$$$4 ^ {15} -1 = 1 \, 073 \, 741 \, 823$
$$$5 ^ {12} -1 = 244 \, 140 \, 624$
$$$6 ^ {10} -1 = 60 \, 466 \, $ 17$
$$$10 ^ {6} -1 = 999 \, $ 99$
$$$12 ^ {5} -1 = 248 \, $ 83$

Gráfico de funciones:



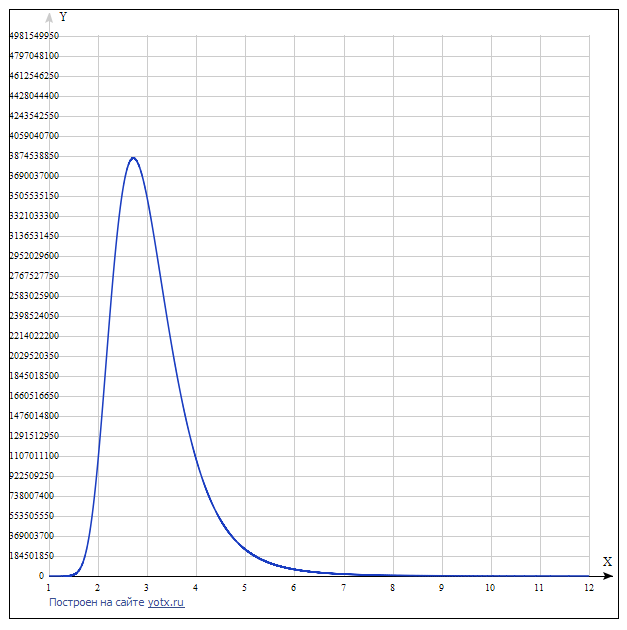
El gráfico muestra que con un aumento en la base de la SS, comenzando con tres, su costo aumenta y la función tiene un extremo superior. Llevándolo a una forma general, puede obtener $$$y = (\ sqrt [x] x) ^ {n} -1$y la función máxima $$$\ sqrt [x] x$logrado cuando $$$x = e$.



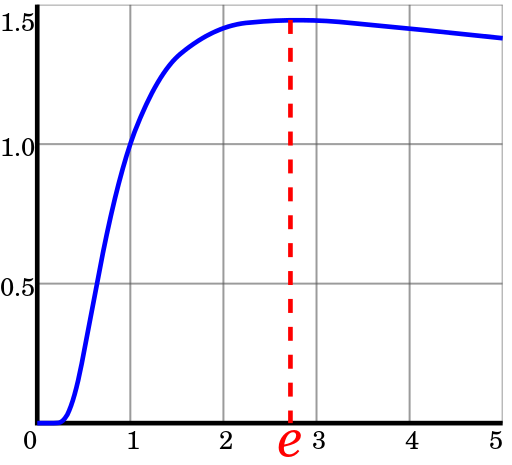
Gráfico de funciones $$$y = \ sqrt [x] x$

Es decir El SS más económico es un sistema lo más cercano posible a $$$e$o 3.

PD: Además, el SS con base 3 es impar, lo que significa que no tiene un problema de redondeo (llevar 0.5 a 0 o 1), y si los números se escriben simétricamente (-1.0.1 en lugar de 0.1.2), entonces aparece simplicidad representan números negativos (10-1 es 8, -101 es -8, donde menos no es un signo, sino parte de un dígito que se puede reemplazar con Z), pero esta es una aritmética completamente diferente)))