No hace mucho tiempo, se tradujo un artículo en Habr sobre cómo usar los tipos de datos algebraicos para garantizar que los estados incorrectos sean inexpresables. Hoy nos fijamos en una forma un poco más generalizada, escalable y segura de expresar lo inexpresable, y Haskell nos ayudará en esto.
En resumen, ese artículo analiza alguna entidad con una dirección postal y una dirección de correo electrónico, así como con la condición adicional de que debe haber al menos una de estas direcciones. ¿Cómo se propone expresar esta condición a nivel de tipo? Se propone escribir las direcciones de la siguiente manera:
type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo
¿Qué problemas tiene este enfoque?
Lo más obvio (y mencionado varias veces en los comentarios sobre ese artículo) es que este enfoque no es escalable en absoluto. Imagine que no tenemos dos tipos de direcciones, sino tres o cinco, y la condición de corrección parece ser "debe haber una dirección postal, o una dirección de correo electrónico y una dirección de oficina, y no debe haber varias direcciones del mismo tipo". Aquellos que lo deseen pueden escribir el tipo apropiado como ejercicio de autoevaluación. La tarea con un asterisco es reescribir este tipo en el caso de que la condición sobre la ausencia de duplicados haya desaparecido del TOR.
Compartir
¿Cómo resolver este problema? Tratemos de fantasear. Primero descomponemos y separamos la clase de dirección (por ejemplo, correo / correo electrónico / número de escritorio en la oficina) y los contenidos correspondientes a esta clase:
data AddrType = Post | Email | Office
Todavía no pensaremos en el contenido, porque no hay nada en el TK con la condición de validez de la lista de direcciones.
Si verificamos la condición correspondiente en el tiempo de ejecución de algún constructor de algún lenguaje OOP ordinario, entonces simplemente escribiríamos una función como
valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs
y lanzaría alguna ejecución si devuelve False .
¿Podemos verificar una condición similar con la ayuda de un temporizador, al compilar? Resulta que sí, podemos, si el sistema de tipos del lenguaje es lo suficientemente expresivo, y el resto del artículo elegiremos este enfoque.
Aquí los tipos dependientes nos ayudarán mucho, y dado que la forma más adecuada de escribir un código validado en Haskell es escribirlo primero en Agde o Idris, cambiaremos nuestros zapatos y escribiremos en Idris. La sintaxis idris está bastante cerca de Haskell: por ejemplo, con la función mencionada anteriormente, solo necesita cambiar ligeramente la firma:
valid : List AddrType -> Bool
Ahora recuerde que, además de las clases de dirección, también necesitamos sus contenidos y codificamos la dependencia de los campos en la clase de dirección como GADT:
data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office
Es decir, si se nos da un valor de fields tipo AddrFields t , entonces sabemos que t es una AddrType AddrType y que los fields contienen un conjunto de campos correspondientes a esta clase en particular.
Sobre esta publicaciónEsta no es la codificación más segura, ya que GADT no tiene que ser inyectiva, y sería más correcto declarar tres tipos de datos separados PostFields , EmailFields , EmailFields y escribir una función
addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields
pero esto es demasiada escritura, lo que para el prototipo no da una ganancia significativa, y en Haskell para esto todavía hay mecanismos más concisos y agradables.
¿Cuál es la dirección completa en este modelo? Este es un par de la clase de dirección y los campos correspondientes:
Addr : Type Addr = (t : AddrType ** AddrFields t)
Los fanáticos de la teoría de tipos dirán que este es un tipo dependiente existencial: si se nos da algún valor de tipo Addr , entonces esto significa que hay un valor t tipo AddrType y un conjunto correspondiente de campos AddrFields t . Naturalmente, las direcciones de una clase diferente son del mismo tipo:
someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762)
Además, si nos EmailFields , entonces la única clase de dirección que es adecuada es Email , por lo que puede omitirla, el temporizador la imprimirá usted mismo:
someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762)
Escribimos una función auxiliar que proporciona la lista correspondiente de clases de dirección de la lista de direcciones, y la generalizamos inmediatamente para trabajar en un functor arbitrario:
types : Functor f => f Addr -> f AddrType types = map fst
Aquí, el tipo de Addr existencial se comporta como una pareja familiar: en particular, puede solicitar su primer componente AddrType (tarea con un asterisco: ¿por qué no puedo pedir el segundo componente?).
Elevar
Ahora pasamos a una parte clave de nuestra historia. Entonces, tenemos una lista de direcciones de List Addr y algunos predicados valid : List AddrType -> Bool , cuya ejecución para esta lista queremos garantizar a nivel de tipos. ¿Cómo los combinamos? Por supuesto, otro tipo!
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst
Ahora analizaremos lo que escribimos aquí.
data ValidatedAddrList : List Addr -> Type where significa que el tipo ValidatedAddrList parametrizado, de hecho, por la lista de direcciones.
Veamos la firma del único constructor MkValidatedAddrList de este tipo: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst . Es decir, toma una lista de direcciones prf y otro argumento prf de tipo valid (types lst) = True . ¿Qué significa este tipo? Por lo tanto, significa que el valor a la izquierda de = es igual al valor a la derecha de = , es decir, valid (types lst) , de hecho, es verdadero.
Como funciona Firma = parece a (x : A) -> (y : B) -> Type . Es decir, = toma dos valores arbitrarios x e y (posiblemente incluso de diferentes tipos A y B , lo que significa que la desigualdad en el idris es heterogénea, y que es algo ambigua desde el punto de vista de la teoría de tipos, pero este es un tema para otra discusión). ¿Qué demuestra entonces la igualdad? Y debido al hecho de que el único constructor = - Refl con una firma de casi (x : A) -> x = x . Es decir, si tenemos un valor de tipo x = y , entonces sabemos que fue construido usando Refl (porque no hay otros constructores), lo que significa que x es realmente igual a y .
Tenga en cuenta que esta es la razón por la cual en Haskell siempre fingiremos, en el mejor de los casos, que estamos probando algo, porque Haskell tiene undefined que habita cualquier tipo, por lo que el argumento anterior no funciona allí: para cualquier x , y término de tipo x = y podría crearse a través de undefined (o a través de una recursión infinita, digamos que en general es lo mismo en términos de teoría de tipos).
También observamos que la igualdad aquí no se entiende en el sentido de Haskell Eq o algún operator== en C ++, sino que es mucho más riguroso: estructural, lo que, simplificando, significa que los dos valores tienen la misma forma . Es decir, engañarlo tan simplemente no funciona. Pero las cuestiones de igualdad se dibujan tradicionalmente en un artículo separado.
Para consolidar nuestra comprensión de la igualdad, escribimos pruebas unitarias para la función valid :
testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl
Estas pruebas son buenas ya que ni siquiera necesita ejecutarlas, es suficiente que el taypcher las verifique. De hecho, reemplacemos True con False , por ejemplo, en el primero de ellos y veamos qué sucede:
testPostValid : valid [Post] = False testPostValid = Refl
Typsekher jura

como se esperaba Genial
Simplificar
Ahora refactoricemos ValidatedAddrList poco nuestra ValidatedAddrList .
En primer lugar, el patrón de comparar un cierto valor con True bastante común, por lo que hay un tipo especial So en el idris para esto: puede tomar So x como sinónimo de x = True . Arreglemos la definición de ValidatedAddrList :
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst
Además, So tiene una conveniente función auxiliar para choose , que en esencia eleva la verificación al nivel de tipos:
> :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof
Nos será útil cuando escribamos funciones que modifiquen este tipo.
En segundo lugar, a veces (especialmente en el desarrollo interactivo) idris puede encontrar el valor prf apropiado prf sí solo. Para que en tales casos no fuera necesario construirlo a mano, hay un azúcar sintáctico correspondiente:
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst
Las llaves indican que este es un argumento implícito de que idris intentará salir de contexto, y auto significa que él también intentará construirlo él mismo.
Entonces, ¿qué nos da esta nueva ValidatedAddrList ? Y proporciona una cadena de razonamiento de este tipo: que val sea un valor de tipo ValidatedAddrList lst . Esto significa que lst es una lista de direcciones, y además, val se creó utilizando el constructor MkValidatedAddrList , al que pasamos este mismo prf y otro valor prf de tipo So (valid $ types lst) , que es casi valid (types lst) = True Y para que podamos construir prf , necesitamos, de hecho, demostrar que esta igualdad es válida.
Y lo más hermoso es que todo esto es comprobado por un tipeador. Sí, la verificación de validez tendrá que realizarse en tiempo de ejecución (porque las direcciones se pueden leer desde un archivo o desde la red), pero el temporizador se asegurará de que esta verificación se realice: sin ella, es imposible crear una ValidatedAddrList . Al menos en idris. En Haskell, por desgracia.
Insertar
Para verificar la inevitabilidad de la verificación, intente escribir una función para agregar una dirección a la lista. Primer intento:
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst)
No, el verificador de errores da en los dedos (aunque no es muy legible, el costo de la valid demasiado complicado):
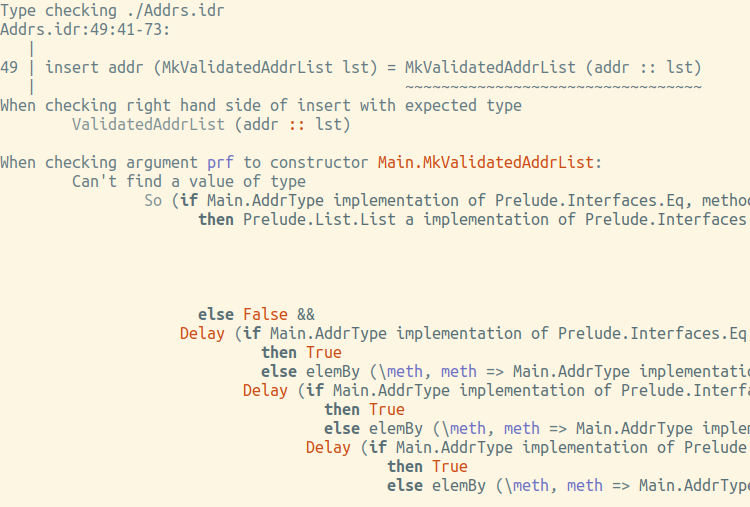
¿Cómo obtenemos una copia de esto? No de otra manera que la mencionada choose . Segundo intento:
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs
Casi typechetsya. "Casi" porque no está claro qué sustituir por rhs . Más bien, está claro: en este caso, la función debe informar de alguna manera un error. Por lo tanto, debe cambiar la firma y ajustar el valor de retorno, por ejemplo, en Maybe :
insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing
Esto está en mosaico y funciona como debería.
Pero ahora surge el siguiente problema no muy obvio, que fue, de hecho, en el artículo original. El tipo de esta función no deja de escribir una implementación de este tipo:
insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing
Es decir, siempre decimos que no podríamos crear una nueva lista de direcciones. Typhechaetsya? Si ¿Es correcto? Bueno, apenas ¿Se puede evitar esto?
Resulta que es posible, y tenemos todas las herramientas necesarias para esto. Si tiene éxito, insert devuelve una ValidatedAddrList , que contiene evidencia de este mismo éxito. ¡Agregue simetría elegante y solicite a la función que devuelva también una prueba de falla!
insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r
Ahora no podemos simplemente tomar y siempre devolver Nothing .
Puede hacer lo mismo para las funciones de eliminación de direcciones y similares.
Veamos cómo se ve todo al final.
Intentemos crear una lista de direcciones vacía:

Es imposible, una lista vacía no es válida.
¿Qué tal una lista de solo una dirección postal?

Bien, intentemos insertar la dirección postal en la lista que ya tiene la dirección postal:

Intentemos insertar el correo electrónico:
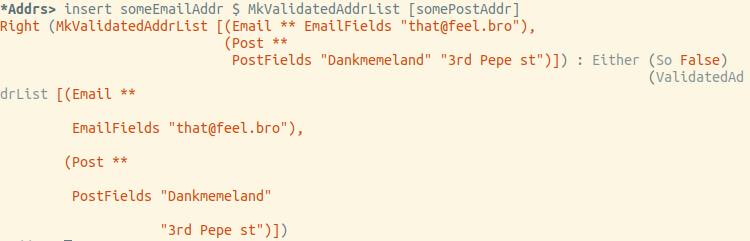
Al final, todo funciona exactamente como se esperaba.
Uf Pensé que serían tres líneas, pero resultó un poco más. Entonces, para explorar qué tan lejos podemos llegar en Haskell, estaremos en el próximo artículo. Mientras tanto, un poco
Reflexionar
¿Cuál es, al final, el beneficio de tal decisión en comparación con la que se da en el artículo, al que nos referimos al principio?
- De nuevo, es mucho más escalable. Las funciones de validación complejas son más fáciles de escribir.
- Está más aislado. El código del cliente no tiene que saber qué hay dentro de la función de validación, mientras que el formulario
ContactInfo del artículo original requiere que esté vinculado. - La lógica de validación se escribe en forma de funciones ordinarias y familiares, para que pueda verificarse de inmediato con una lectura reflexiva y probarse con pruebas de tiempo de compilación, en lugar de derivar el significado de validación de un formulario de tipo de datos que representa un resultado ya verificado.
- Es posible especificar con mayor precisión el comportamiento de las funciones que funcionan con el tipo de datos que nos interesa, especialmente en el caso de no pasar la prueba. Por ejemplo, la
insert escrita como resultado es simplemente imposible de escribir incorrectamente . Del mismo modo, uno podría escribir insertOrReplace , insertOrIgnore y similares, cuyo comportamiento está completamente especificado en el tipo.
¿Cuál es el beneficio en comparación con una solución OOP como esa?
class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } };
- El código es más modularizado y seguro. En el caso anterior, un cheque es una acción que se verifica una vez y que luego olvidaron. Todo se basa en la honestidad y el entendimiento de que si tiene un
ValidatedAddrListClass , su implementación una vez que se verificó allí. El hecho de esta verificación de la clase no puede seleccionarse como un cierto valor. En el caso de un valor de algún tipo, este valor puede transferirse entre diferentes partes del programa, usarse para construir valores más complejos (por ejemplo, nuevamente, negar esta verificación), investigar (ver el siguiente párrafo) y generalmente hacer lo mismo que solíamos hacer. con valores - Dichas comprobaciones pueden utilizarse en la coincidencia de patrones (dependientes). Es cierto que no en el caso de esta función
valid y no en el caso de idris, es dolorosamente complicado e idris es penosamente aburrido, de modo que la información útil para los patrones puede extraerse de la estructura valid . Sin embargo, valid puede reescribirse en un estilo de coincidencia de patrones un poco más amigable, pero esto está más allá del alcance de este artículo y generalmente no es trivial en sí mismo.
¿Cuáles son las desventajas?
Solo veo un defecto fundamental grave: valid es una función demasiado estúpida. Solo devuelve un bit de información, ya sea que los datos hayan pasado la validación o no. En el caso de los tipos más inteligentes, podríamos lograr algo más interesante.
Por ejemplo, imagine que el requisito de unicidad de direcciones ha desaparecido de TK. En este caso, es obvio que agregar una nueva dirección a la lista de direcciones existente no invalidará la lista, por lo que podríamos probar este teorema escribiendo una función con el tipo So (valid $ types lst) -> So (valid $ types $ addr :: lst) y úselo, por ejemplo, para escribir con seguridad de tipos siempre exitoso
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst)
Pero, por desgracia, teoremas como la recursividad y la inducción, y nuestro problema no tiene una estructura inductiva elegante, por lo tanto, en mi opinión, el código con roble booleano valid también valid bueno.