En este artículo, crearemos un modelo de controlador basado en la biblioteca estándar de modelado estructural (sin usar una biblioteca lista de bloques de regulación difusos).
Como objeto de control, un modelo de un motor de turbina de gas del libro de texto de V.I. Gosteva "Reguladores difusos en sistemas de control automático"
Hagamos una comparación con los reguladores PID y SDA.
Declaración del problema.
La diferencia entre un motor de turbina de gas (motor de turbina de gas) y un motor de turborreactor (motor de turborreactor) es que en un motor de turbina de gas toda la energía se elimina a través del eje. En los motores turborreactores, la energía se libera en forma de corriente en chorro.
Los motores de turbina de gas (GTE) se usan ampliamente en las industrias de gas y aviación, donde son la base de las unidades de bombeo de gas y las plantas de energía de los aviones, en los accionamientos de turbogeneradores eléctricos industriales de plantas de energía pico y móvil, en plantas de energía marina y otras instalaciones industriales donde se requiere el desarrollo de grandes capacidades individuales. (de 1 a 25 MW) en una unidad con su peso y dimensiones mínimas.
Se impone un conjunto de requisitos a los motores de turbina de gas relacionados con su confiabilidad, eficiencia energética, seguridad y respeto al medio ambiente durante la operación. Junto con estos requisitos, los requisitos para la calidad de los transitorios asociados con el lanzamiento de la unidad, un cambio brusco en la carga seleccionada (potencia) son relevantes. En muchos aspectos, la satisfacción de estos requisitos radica en el sistema de control automático (ACS) del motor de turbina de gas.
Un motor de turbina de gas típico utilizado en la industria es un motor de turboeje, cuyo circuito se muestra en la Figura 1.
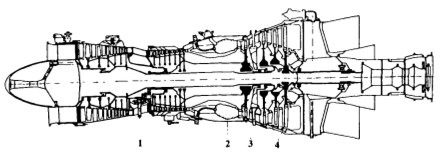
Figura 1. Esquema de un motor de turbina de gas industrial típico:
1- compresor; 2 - una cámara de combustión; 3 - turbina de compresor; 4 - turbina de potencia.
El motor es una máquina rotativa en la cual el aire se comprime en el compresor 1, el combustible suministrado al aire se quema en la cámara de combustión 2, parte de la energía se toma de los gases calientes en la turbina del compresor 3, consumida por el compresor 1, 4 gases en la turbina de potencia. expandiendo crear energía tomada del motor por el consumidor.
En la gran mayoría de los motores de turbina de gas, la velocidad del rotor es una cantidad controlada. Como factor de control en el ACS, la velocidad del rotor n se utiliza el consumo de combustible GT en la cámara de combustión. En diferentes modos de funcionamiento y en diversas condiciones externas, los parámetros del motor cambian significativamente.
Considere un motor de turbina de gas (GTE) como un objeto de control no estacionario para el que la velocidad del rotor es variable y el consumo de combustible G T es la acción de control. Linealizando la dependencia del momento de la turbina - M T y el momento del compresor - M K , de la velocidad del rotor y sin tener en cuenta la influencia de la capacidad térmica y de masa del motor para un modo de funcionamiento particular, escriba la función de transferencia del motor de la siguiente manera:
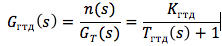
donde la ganancia y la constante de tiempo se definen como:
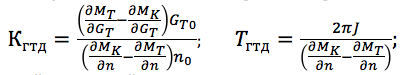
Además, las señales de entrada y salida se registran en desviaciones relativamente adimensionales del estado estacionario (n = Δn / n 0 ; G T = ΔG / G TO , donde los valores básicos de los parámetros se seleccionan para un modo de operación del motor específico, por ejemplo, nominal o máximo). En diferentes modos de operación y bajo diversas condiciones externas, la ganancia y la constante de tiempo del motor cambian significativamente, por lo tanto, para cada modo, es necesario determinar sus propios valores de K GTD y T GTD .
Tenga en cuenta que la función de transferencia G de los motores de turbina de gas para un objeto de control inestable, como un motor de turbina de gas, se obtiene mediante el método de coeficientes "congelados" bajo la condición de un cambio bastante lento en los parámetros del objeto.
En la Figura 2 se muestra el diagrama de bloques de un sistema electromecánico analógico para controlar automáticamente la velocidad del rotor de un motor.
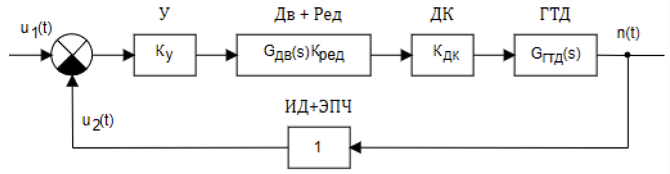
Figura 2. Diagrama de bloques de un SAR GTE analógico
La frecuencia de rotación se establece mediante el voltaje u 1 (t) y se cambia mediante un sensor de ID de pulso, cuya frecuencia de la señal de salida está determinada por la expresión:
f = kmn, donde n es el número de revoluciones del motor, m es el número de dientes del engranaje, k es la relación de engranaje. El voltaje alterno tomado de la salida ID usando el convertidor de frecuencia electrónico del EPC se convierte en una señal u2 (t), cuyo valor es proporcional al número de revoluciones del motor - n. El voltaje u2 (t) se compara con el voltaje de referencia y la señal de error después de que el amplificador U se suministra al motor asíncrono bifásico Dv, que regula la válvula de mariposa del CC a través de la caja de cambios Roja, cambiando el caudal de combustible que ingresa al motor de turbina de gas. Un sensor de pulso junto con un convertidor de frecuencia electrónico puede describirse mediante un enlace proporcional con una función de transferencia igual a la unidad. En este caso, el sistema en sí tiene una única retroalimentación.
Teniendo en cuenta la conexión en serie del amplificador, el motor de inducción, la válvula de mariposa, la unidad de turbina de gas y el sensor de frecuencia con un convertidor de frecuencia electrónico como un objeto de control común, y utilizando un regulador digital difuso, todo el diagrama de bloques de la Figura 2 se puede reducir al diagrama de bloques de la Figura 3. Además, todos Las funciones de transferencia de los enlaces se reducen a una función de transferencia común G 0 (s).
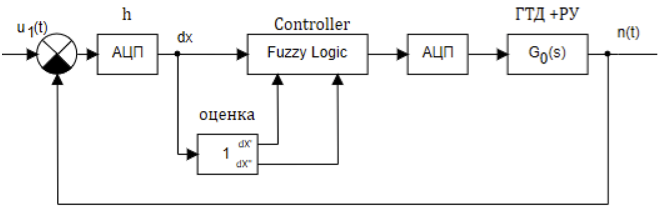
Figura 3. La estructura del sistema de control con un controlador difuso.
La función de transferencia general G0 (s) se puede escribir como:
G 0 (s) = G (s) K EDITAR A G (s) = α [s (s + a) (s + b)] -1 , donde
α = ab K K EDITAR EN K ,
a = 1 / T DW ,
b = 1 / T GTE
Por ejemplo, suponemos que las dependencias de la función de transferencia en el tiempo de operación toman los siguientes valores:
T GTD (t) = 0.9849 - 0.1188 × t + 0.0063 × t 2 - 0.00012 × t 3 ;
α (t) = 16.5475 - 4.4469 × t + 0.4843 × t 2 - 0.02315 × t 3 + 0.0004 × t 4 ;
T DW = 0.35 s.
En el estudio del sistema de control, suponemos que la función dada de cambiar la velocidad de rotación del rotor de un motor de turbina de gas está establecida por el voltaje de entrada u (t)
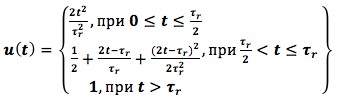
donde τ r es el tiempo de aceleración del motor. Tomamos τ r = 6 seg.
Creando un modelo dinámico
En la Figura 4 se presenta un modelo simplificado del motor. En este modelo, utilizamos parámetros variables de bloques típicos que cambian durante la simulación de la dependencia dada anteriormente.
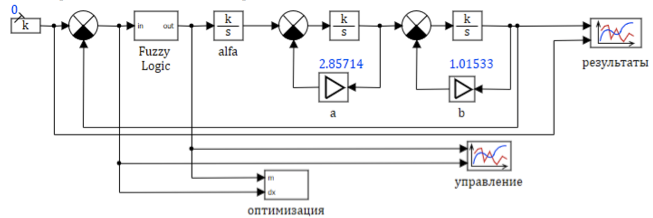
Figura 4. Diagrama estructural de un modelo de motor de turbina de gas.
Los coeficientes de los amplificadores alfa, a, b se calculan utilizando un lenguaje de script, el texto del programa a continuación:
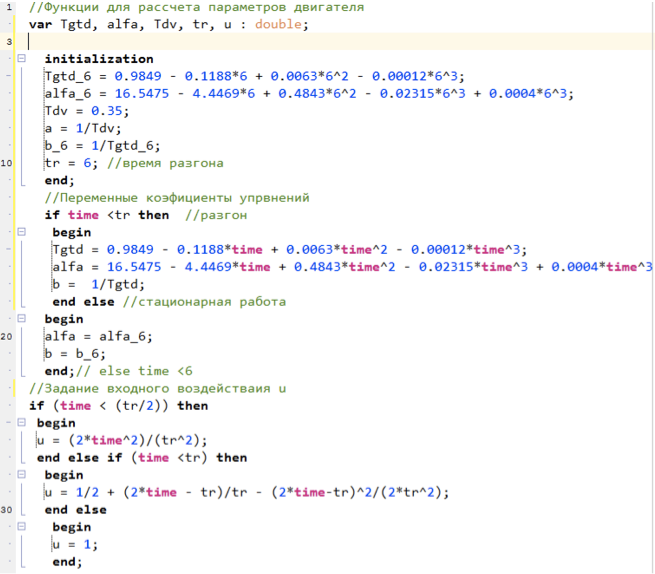
Figura 5. Script para calcular los parámetros del modelo.
Perilla de control de lógica difusa
El regulador de control toma la entrada del desajuste entre el valor establecido y el valor obtenido del modelo, y debe calcular la acción de control.
Intentemos ensamblar un controlador basado en lógica difusa, usando solo bloques matemáticamente estándar de modelado estructural, sin usar una biblioteca especializada.
Una descripción de los principios de control basada en la lógica difusa se puede encontrar en el artículo anterior sobre el centro, o en la descripción de cómo crear una biblioteca especializada de bloques aquí (cuidadosamente, blasfemias).
Cualquier controlador basado en lógica difusa realiza la siguiente secuencia de transformaciones:
- Fases de las variables de entrada. El valor de la variable se reemplaza por un conjunto de términos.
- Activación de las conclusiones de las reglas de la lógica difusa.
- Acumulación de conclusiones para cada variable lingüística.
- Desfazificación de variables de salida.
Para controlar el motor, utilizaremos tres variables continuas, que se calculan en función de una señal:
- desviación
- desviación derivada (desviación de la tasa de cambio);
- La segunda derivada de la desviación (aceleración de los cambios en las desviaciones).
El esquema de cálculo se presenta en la Figura 6:
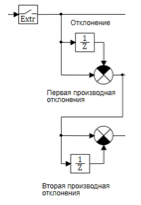
Figura 6. Cálculos de las desviaciones derivadas primera y segunda.
El bloque extrapolador cuantifica la señal que ingresa al controlador con un período de 0.01 segundos. La primera y segunda derivada se calculan usando fórmulas de diferencia:
 donde:
donde:
u (t) es la desviación actual en el tiempo t;
u (t-Δt) es la desviación en el tiempo t - Δt;
u '(t) es el valor actual de la derivada de la desviación en el tiempo t;
u '(t-Δt) es el valor de la derivada de la desviación en el tiempo t - Δt;
u '' (t) es el valor actual de la segunda derivada de la desviación en el tiempo t;
u '' (t-Δt) es el valor de la segunda derivada de la desviación en el tiempo t - Δt;
Δt es el período de cuantificación.
La división por Δt se lleva a cabo en la unidad de comparación.
Como resultado de este bloque, se crean tres variables lingüísticas: desviación, primera variable de desviación, segunda variable de desviación.
Para resolver el problema del control difuso, usaremos solo dos términos para cada variable lingüística.
Desviación: menos, más;
La primera derivada de la desviación está disminuyendo, aumentando;
La segunda derivada de la desviación: se ralentiza, se acelera.
Para calcular el valor de la función de pertenencia μ para cada término, utilizamos una función lineal con saturación. Esta función para el término es más de 0 cuando el valor de entrada es mínimo y 1 cuando el valor de entrada es máximo. Para un término menor, esta función toma el valor 1 cuando la variable es igual al mínimo y 0 cuando la variable es máxima. (ver figura 7)
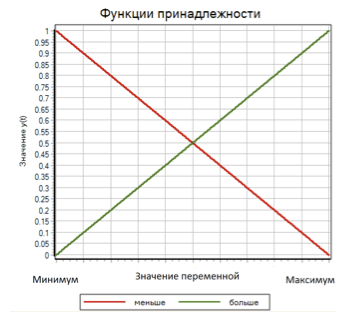
Figura 7. Funciones de membresía para términos cada vez menos.
Por lo tanto, para cada una de las tres variables de entrada (desviación, la primera derivada de la desviación, la segunda derivada de la desviación), hay dos términos más y menos, el valor de las funciones de membresía μ i que varían linealmente de 0 a 1 dependiendo del valor de la entrada variable.
Como la variable lingüística de salida, utilizamos el efecto de salida, que también tiene solo dos términos para reducir e incrementar.
Del diagrama modelo de la Fig. 4 es obvio que si la desviación es menor que 0, entonces el valor es mayor que el valor especificado y debe reducirse. Si la desviación es mayor que 0, entonces la función es menor que la especificada y debe aumentarse.
Las reglas lógicas para los dos términos se verán así:
- Si menos y disminuye y disminuye la velocidad => disminuir.
- Si más y aumenta y acelera => aumenta.
Para activar las reglas de inferencia difusa, utilizamos la función mínima para el difuso y el operador. Las fórmulas calculan el valor de las funciones de membresía para los términos de la función de salida:
μ
disminución = MIN (μ
menos , μ
disminuye , μ
disminuye la velocidad )
μ
aumentar = MIN (μ
más , μ
aumenta , μ
acelera )
Para garantizar la conversión de términos a valores de impacto específicos (acumulación y desnazificación), utilizamos el algoritmo Tsukamoto como centro de gravedad de los puntos.
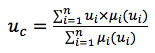 donde
donde
u c es la función resultante;
u i es el valor de la función para el término i;
μ i es el valor de la función de membresía para los términos de la función.
En nuestro caso, la función resultante para dos términos se calcula mediante la fórmula:
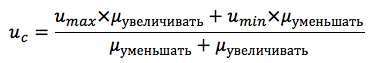
El esquema general del algoritmo de inferencia difusa se presenta en la Figura 8:
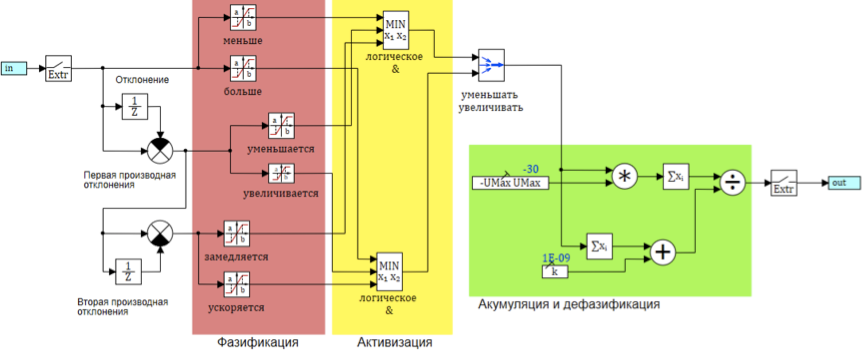
Figura 8. El esquema del algoritmo de inferencia difusa
Para que este algoritmo funcione, debemos establecer los valores mínimo y máximo para 6 términos de tres variables lingüísticas (desviación, primera derivada de la desviación, segunda derivada de la desviación). Para reducir los cálculos, suponemos que la desviación es simétrica con respecto a cero. Entonces es suficiente para nosotros encontrar 3 valores absolutos, uno para cada variable.
deltMax: desviación máxima. Establece los valores de los términos less, more (-deltMax, deltaMax);
divMax es la derivada máxima de la desviación. Establece los valores de los términos disminuye, aumenta (-divMax, divMax);
div2Max es la segunda derivada máxima. Establece los valores de los términos ralentiza, acelera (-div2Max, div2Max).
El impacto máximo y mínimo de umin y umax están determinados por las características de diseño y en este ejemplo se toman igual a +30 y -30.
Ajuste del regulador por optimización.
Para seleccionar los coeficientes, utilizamos el mismo esquema de optimización que utilizamos en experimentos anteriores con lógica difusa.
Como criterio de optimización, tomamos la desviación estándar de no más de 0.001 y el número de conmutaciones en la unidad de control no más de 25. Para la conmutación, tomamos un cambio en el signo de la acción de control.
El circuito del bloque de configuración del controlador se muestra en la Fig. 9)
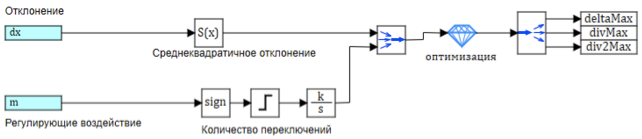
Figura 9. Configuración de parámetros de salida difusos.
Como resultado de la operación del bloque, se obtuvieron los siguientes parámetros
deltMax = 0.00746;
divMax = 0.2657;
div2Max = 25.13;
Los resultados de la transición se presentan en la Figura 10.
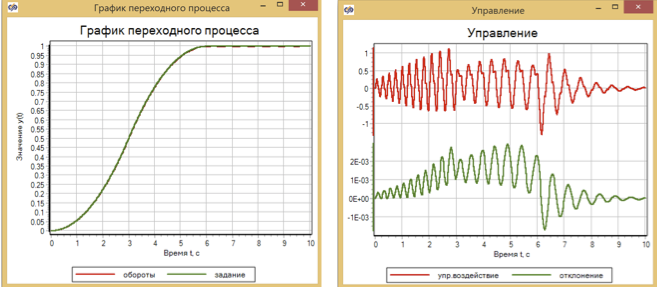
Figura 10. Control transitorio y motor utilizando lógica difusa.
La desviación máxima de las revoluciones del conjunto después de la optimización fue 2.5 × 10-3 . Lo cual, en principio, no es malo, pero en el libro de V.I. Las desviaciones de los huéspedes en el modelo después de la configuración fueron dos órdenes de magnitud más pequeñas: el máximo fue 5 × 10-5 .
A modo de comparación, presentamos los resultados de la operación del controlador PID Fig. 11 y las reglas de tráfico Fig. 12 para el mismo modelo de motor simplificado. Los parámetros de estos reguladores también fueron seleccionados por el método de optimización.
Como resultado, se obtiene una desviación mayor para el controlador PID que para un controlador basado en lógica difusa: aproximadamente 6 × 10-3 , y para un controlador de tráfico que usa la segunda derivada, la desviación es aproximadamente 3 × 10-3 (ver 13). Además, en todos los gráficos se puede ver que cuando cambia el impacto especificado (cambios en las secciones 3 segundos, 6 segundos), la calidad de la regulación cambia.
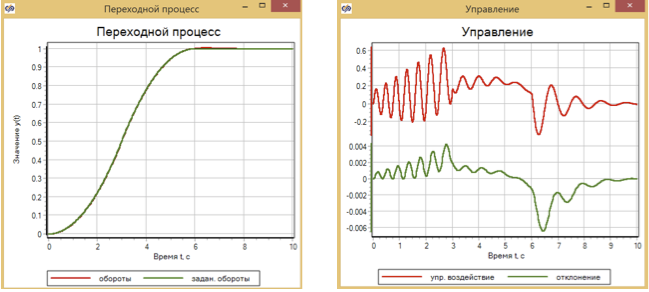
Figura 11. Control transitorio y motor utilizando un controlador PID.
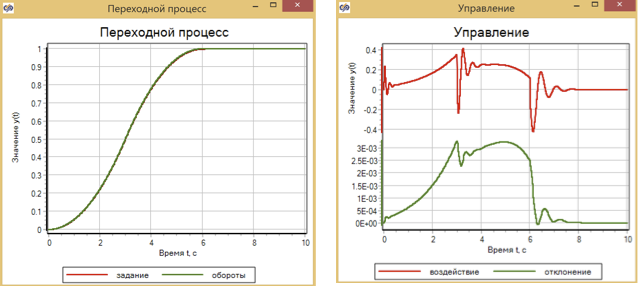
Figura 12. Proceso transitorio y control del motor con la ayuda del controlador de tráfico.
Para arrancar el motor, la función de transición se utiliza en forma de un cambio suave en la velocidad. También ajustamos los reguladores mediante el método de optimización para un control óptimo de acuerdo con esta ley. Tratemos de aplicar un efecto gradual y veamos cómo los reguladores, inicialmente optimizados para un proceso de transición sin problemas, pueden hacer frente.
Como efecto, usamos un paso de 0 a 1 a los 3 segundos del proceso.
Los resultados del experimento se presentan en las figuras 13-15.
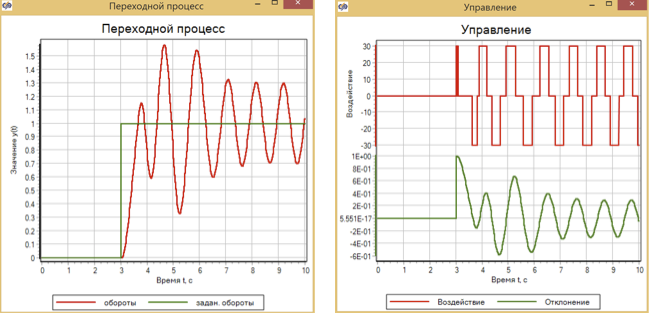
Figura 13. Proceso y control transitorios con una acción de control gradual con un controlador de lógica difusa.
Se puede ver que un regulador sintonizado para una aceleración suave del motor no hace frente al control durante una acción gradual, y el sistema entra en modo de oscilación automática.
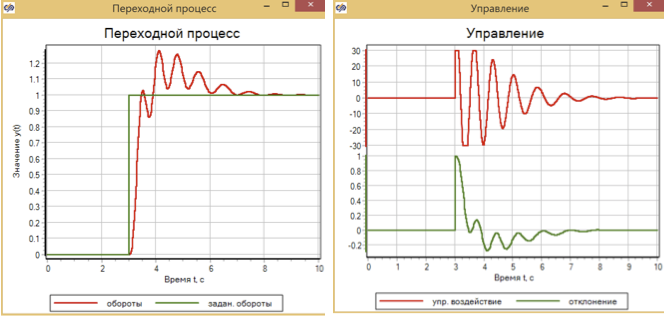
Figura 14. Proceso y control transitorio con acción de control de pasos con controlador PID.
Un controlador PID sintonizado a un proceso uniforme, con un efecto gradual, proporciona una transición a un tiempo predeterminado, pero al mismo tiempo hay un sobreimpulso del 30% y un proceso oscilatorio en 4 segundos.
El controlador de tráfico, configurado para una regulación suave, con un efecto gradual proporciona una transición suave sin sobreimpulso (Fig. 14)
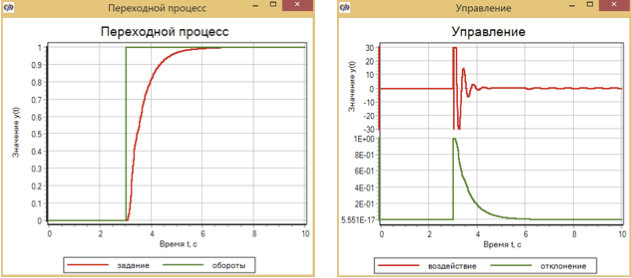
Figura 15. El proceso de transición y control con una acción de control escalonada con un controlador de tráfico.
Conclusiones
Estos experimentos numéricos mostraron que un controlador basado en lógica difusa proporciona un control más preciso de las revoluciones de un modelo de motor simple con un cambio suave en el valor establecido que el PID y SDA.
Sin embargo, tal configuración, como se vio después, no garantiza la estabilidad del regulador durante una acción gradual.
Al mismo tiempo, para un modelo simplificado del motor, un controlador basado en lógica difusa en el caso de una acción escalonada resultó ser peor que un controlador PID o SDA.
Enlace al archivo con los proyectos del artículo para el autoestudio