Introduccion
Han pasado cuatro meses desde la publicación del artículo sobre mi intento de una implementación de bajo nivel del
árbol de prefijos . A pesar de todos mis esfuerzos, el límite en el cual mi implementación previa del árbol de prefijos resultó ser capaz fue de ~ 80 mil palabras por segundo. Luego pasé mucho tiempo y energía, pero el resultado sería adecuado solo como trabajo de laboratorio en informática.
Muchos me dijeron: “¡No inventes una bicicleta que ya hemos inventado! Usa la solución llave en mano. La dificultad es que no podría usar algo que no entiendo al menos en términos generales.
Creo que entendí el árbol de prefijos, y esto es lo que logré lograr.
Principio de funcionamiento
No sé muy bien inglés, así que de los muchos artículos que leí sobre el tema de los árboles de prefijos, es probable que parte de la información no me haya llegado. Por lo tanto, se me ocurrió cómo organizar todo, entendiendo solo el principio básico del árbol de prefijos. Para aquellos que no saben, intentaré describirlo más claramente de lo que está escrito en Wikipedia. Entonces le expliqué lo que le estaba haciendo a mi esposa.
El árbol de prefijos es una estructura lógica para almacenar datos que se pueden representar como un índice de tarjeta de libros en una biblioteca. Cada caja tiene un número. Cada cuadro corresponde a una letra específica del alfabeto. En el interior se encuentran los números de los siguientes cajones, una apertura que puede encontrar a continuación y así sucesivamente. Cuando no hay nada dentro del cuadro, esto significa que la letra de este cuadro es la última en la palabra. El problema es que algunas cajas permanecen casi vacías, porque contienen 1 o 2 números, y el espacio restante está vacío.
Para resolver este problema, han aparecido muchas variedades de árboles de prefijos, que incluyen: HAT-trie, trie de doble matriz, trie de triple matriz. Fue precisamente el hecho de que no podía entender completamente el principio de su trabajo lo que me empujó a un árbol tan simple como un archivo de tarjeta de biblioteca.
La última vez logré implementar una implementación de consumo de memoria bastante económica de un árbol de prefijos simple. Continuando con esta metáfora con un índice de tarjeta de biblioteca, hice cajones en mi archivador de diferentes tamaños, para el alfabeto completo, el cuadro es el más grande, para 1 letra el más pequeño.
Logré implementar exactamente el mismo esquema PHP en C.
1. Cada letra de la palabra según la tabla establecida se codifica con un número del 2 al 95. Por ejemplo, la palabra "abv" se codifica con tres números: 11, 12, 13. Para obtener el máximo rendimiento,
uint8_t abc[256][256] = {}; una matriz bidimensional de números de 1 byte de
uint8_t abc[256][256] = {}; Para convertir un programa, lee una línea por 1 byte, trata de tomar el valor de cada byte en nuestra matriz. Por ejemplo, el código de dígitos es 1 = 49, por lo que buscamos
abc[49][0]; . Si hay un valor diferente a '\ 0', entonces este es el código de nuestra carta, recuérdelo y pase al siguiente byte. En nuestro caso, la palabra "abv" consiste en una secuencia de 6 bytes, dos bytes por letra: 208, 176, 208, 177, 208, 178. Dado que la codificación utf-8 está diseñada para que los primeros bytes de caracteres de un solo byte nunca coincidan con los primeros bytes de varios bytes. , en nuestra matriz
abc[208][0] = 0; .
Sin embargo, para los pares de bytes hay algunas coincidencias:
/* [11] */ abc[208][176] = 11; /* [12] */ abc[208][177] = 12; /* [13] */ abc[208][178] = 13;
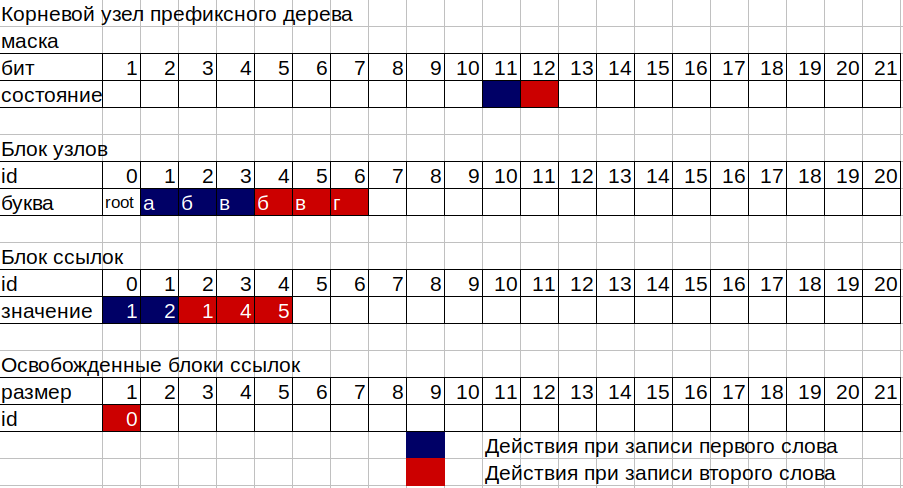
2. Ahora necesitamos escribir los números 11, 12 y 13 en las cajas de nuestro árbol. El árbol consta de 2 bloques de memoria no explosivos separados, el primero es un bloque de nodos, el segundo es un bloque de enlaces, así como dos contadores de nodos ocupados y celdas ocupadas de un bloque de enlaces. Cada nodo de árbol consta de 16 bytes, 12 bytes de una máscara de bits y 4 bytes para almacenar la identificación del bloque de enlace. La máscara le permite almacenar números de 2 a 96 bits. El primer bit de la máscara se usa para marcar el final de la palabra en este nodo. Cada nodo puede corresponder a la identificación del bloque de enlace si al menos 1 letra está escrita en este nodo, o no corresponde si el nodo es una "hoja" en términos de árboles, es decir, una palabra simplemente termina en él. Expresado en una biblioteca, un cajón vacío.
3. Tome la máscara del primer nodo (raíz). trie-> nodos [0] .mask; Contamos los bits generados en esta máscara, comenzando desde el segundo (el primero para el indicador de fin de palabra). Si no se levantan bits en la máscara, es decir Como el nodo está vacío, necesitamos un bloque de enlace de tamaño 1 para almacenar nuestro número 11, tome el número del contador de referencia de enlace del bloque y aumente el valor anterior en uno (porque necesitamos el tamaño 1). Tomamos el número del contador de nodos y también aumentamos el valor anterior en 1. Escribimos la identificación del bloque de enlace, que es el número obtenido del contador de bloque de enlace, en nuestro nodo raíz. Y en esta identificación del bloque de enlace, escriba la identificación del nuevo nodo, es decir, el número obtenido del contador de nodos. Ahora, además del nodo raíz (id 0), tenemos un nodo de la letra "a" (id 1). Para escribir el número 12 correspondiente a la letra "b", hacemos lo mismo, pero con el nodo de la letra "a".
4. En la última letra "c" no necesitamos un lugar en el bloque de enlaces, ya que tendremos el último nodo en la rama o la hoja de nodo. Tal nodo tiene solo 1 bit en la máscara elevada.
5. La parte más difícil del trabajo de un árbol ocurre cuando se escribe en un nodo en el que ya se han escrito algunas letras. En este caso, el esquema de operación es el siguiente:
Supongamos que queremos agregar la palabra "bvg" (12, 13, 14) a nuestro árbol, en el que la palabra "abv" (11, 12, 13) ya está escrita. Contamos los bits en la máscara del nodo raíz al bit de la carta que nos interesa. Tenemos la letra "b" con el código 12, lo que significa que el bit de esta letra es 12, en la máscara de 1 a 12 bits, el bit 11 de la letra "a" ya se ha elevado. Entonces, tenemos el tamaño actual del bloque de enlace para el nodo raíz 1. Escribimos la segunda letra, por lo que ahora necesitamos un bloque de enlace de tamaño 2. Aquí entra en juego el registro de bloques liberados, en el que los nodos ya no usan la identificación y el tamaño de las secciones en el bloque de enlace. arbol Nuestra antigua identificación del bloque de enlace para el nodo raíz de tamaño 1 solo ingresa al registro de secciones libres de tamaño 1, ya que nuestro nodo raíz necesita un tamaño mayor. Nuestro registro no tiene una sección adecuada de tamaño 2 y nuevamente tomamos el valor del contador del bloque de enlaces como la nueva identificación del bloque de enlaces, aumentando el contador en 2. En la nueva dirección del bloque de enlaces en el mismo orden en que se ubican los bits en la máscara de nodo, escribimos el valor de identificación nodo del antiguo bloque de enlaces para la letra "a" de la primera palabra y el valor del nodo recién creado de la letra "b" de la segunda palabra.
Velocidad de trabajo
Suena el tambor ... ¿Recuerdas el último resultado? Alrededor de 80 mil palabras por segundo. El árbol fue creado del diccionario de todas las palabras rusas OpenCorpora 3 039 982 palabras. Y aquí está lo que pasó ahora:
yatrie creation time: 4.588216s (666k wps) yatrie search time 1 mln. rounds: 0.565618s (1.76m wps)
ACTUALIZACIÓN 11/01/2018:En la versión 0.0.2, era posible aumentar la velocidad casi 2 veces reemplazando funciones completas con funciones macro, así como cambiando la estructura de la máscara de nodo a uint32_t mask [3], anteriormente era uint8_t mask [12].
También se agregaron macros LIKELY () UNLIKELY () para predecir los resultados esperados en esos bloques if (), donde sea posible.
ACTUALIZACIÓN 11/05/2018:Torcido un poco más. Me las arreglé para que funcionara bien incluso compilando -O3 y -Ofast. La velocidad de búsqueda en el árbol es ~ 0.2 μs o 0.2c por 1 millón de repeticiones. Aparentemente, esta velocidad se obtuvo debido a la transición a un formato diferente de la máscara. Anteriormente, había 12 bytes de 8 bits, y ahora 3 int32 y una función muy rápida para contar bits en int32.
¿Qué tan compacto es esto?
El diccionario OpenCorpora especificado toma ~ 84MB, que no es mucho peor que libdatrie, que da ~ 80MB.
→
Código fuenteBienvenido