Implementación del algoritmo Levenberg-Marquardt para optimizar redes neuronales en TensorFlow

Este es un tutorial de la biblioteca TensorFlow. Considérelo un poco más profundo que en los artículos sobre el reconocimiento de números escritos a mano. Este es un tutorial sobre métodos de optimización. Aquí no puedes prescindir de las matemáticas. Está bien si lo olvidaste por completo. Recordar. No habrá evidencia formal y conclusiones complejas, solo el mínimo necesario para la comprensión intuitiva. Para comenzar, algunos antecedentes sobre cómo este algoritmo puede ser útil para optimizar una red neuronal.

Hace seis meses, un amigo me pidió que le mostrara cómo hacer una red neuronal en Python. Su empresa produce instrumentos para mediciones geofísicas. Varias sondas diferentes durante la perforación miden un conjunto de señales asociadas con los parámetros del entorno que rodea el pozo. En algunos casos complejos, calcule con precisión los parámetros ambientales de las señales durante mucho tiempo, incluso en una computadora potente, y es necesario interpretar los resultados de las mediciones en el campo. Hubo una idea de contar varios cientos de miles de casos en un clúster y entrenar una red neuronal en ellos. Dado que la red neuronal es muy rápida, puede usarse para determinar parámetros que sean consistentes con las señales medidas, justo en el proceso de perforación. Los detalles están en el artículo:

Kushnir, D., Velker, N., Bondarenko, A., Dyatlov, G. y Dashevsky, Y. (29 de octubre de 2018). Simulación en tiempo real de la herramienta de resistividad azimutal profunda en modelo de fallas 2D utilizando redes neuronales (ruso). Sociedad de Ingenieros de Petróleo. doi: 10.2118 / 192573-RU

Una tarde, mostré cómo los keras podían implementar una red neuronal simple, y un amigo en el trabajo comenzó a entrenar sobre los datos contados. Después de un par de días, discutimos el resultado. Desde mi punto de vista, parecía prometedor, pero un amigo dijo que necesitaba cálculos con la precisión del dispositivo. Y si el error cuadrático medio resultó ser alrededor de 1, entonces se necesitaba 1e-3. 3 pedidos menos. Mil veces

Los experimentos con arquitectura de red neuronal, normalización de datos y enfoques de optimización no arrojaron casi nada. Un par de semanas después, un amigo llamó y dijo que instaló MatLab y resolvió el problema mediante el método Levenberg-Marquardt (en adelante llamaremos a LM ). Se optimizó durante mucho tiempo (varios días), no funcionó en la GPU, pero el resultado fue el correcto. Parecía un desafío.

Falló una búsqueda rápida de un optimizador LM listo para keras o TensorFlow. Me encontré solo con la biblioteca pyrenn, pero su funcionalidad me pareció pobre. Decidí implementarlo yo mismo. A primera vista, todo parecía simple, y dos noches deberían haber sido suficientes. Tomó más tiempo. Hubo dos problemas:

1. TensorFlow. Un montón de artículos, pero casi todos los niveles "pero escribamos hola mundo reconocimiento de dígitos escritos a mano".
2. Matemáticas Olvidé mucho, y a los autores de artículos matemáticos no les importan las personas como yo: fórmulas sólidas sin explicación, "¡obviamente!" Y así sucesivamente.

Como resultado, escribió un artículo para aquellos que olvidaron las matemáticas y quieren entender TensorFlow un poco más profundo, pero sin hardcore. El artículo tiene mucho texto y poco código. La opción opuesta, cuando hay poco texto y mucho código, es aquí Jupyter Notebook Levenberg-Marquardt .

Conozca la función Rosenbrock

Generaremos datos de entrenamiento mediante la función Rosenbrock , que a menudo se utiliza como punto de referencia para algoritmos de optimización:

$$ $$f (x, y) = (a-x) ^ 2 + b (y-x ^ 2) ^ 2$$

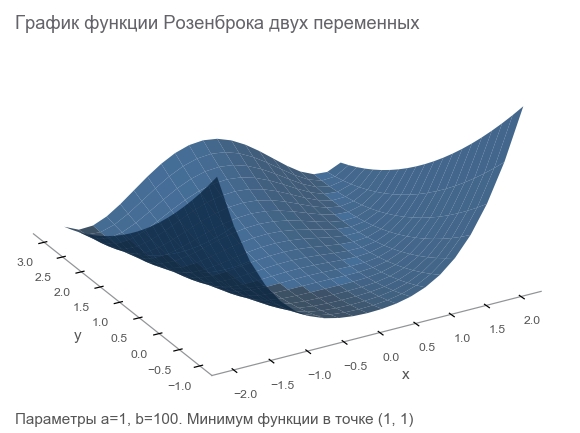
¿Por qué ella es buena?

• Hermoso horario. Se llama el valle de Rosenbrock y la función de banana de Rosenbrock no traducible .
• El mínimo global está dentro de un valle plano, parabólico, largo y estrecho. Encontrar un valle es trivial, y un mínimo global es difícil.
• Hay una opción multidimensional. No es tan fácil encontrar una buena función para muchas variables.

Comenzaremos a escribir código a partir de él conectando las bibliotecas necesarias para un trabajo posterior:

import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2 

Nosotros planteamos el problema

Como estábamos hablando de un dispositivo de medición, continuemos usando la analogía. Nuestro dispositivo en un mundo ficticio puede medir coordenadas $$$(x, y)$ y altura $$$z$ . Los físicos estudiaron el mundo y dijeron: " Sí, ¡esta es Rosenbrock! Conociendo las coordenadas, puede calcular con precisión la altura, no necesita medirla ". En otras palabras, los científicos nos dieron un modelo. $$$z = rosenbrock (x, y, a, b)$ que depende de los parámetros $$$(a, b)$ . Estos parámetros, aunque constantes en un mundo ficticio, son desconocidos. Necesitan ser encontrados.

Llevamos a cabo una serie de experimentos que dieron $$$m$ puntos $$$(x_1, y_1, z_1), (x_2, y_2, z_2), ..., (x_m, y_m, z_m)$ :

 # (2.5, 2.5) -   ,  ,     data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0] 

La primera forma de optimizar es intentar adivinar los parámetros. Usamos la biblioteca Numpy:

 x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] #   =5  b=5? a_guess, b_guess = 5., 5. #  -hat   ,   , #   ,   ,   .   #     ^   - # .    hat. z_hat = rosenbrock(x, y, a_guess, b_guess) 

¿Cómo entender lo equivocados que estamos? Contar residuos - tamaños de error. $$$m$ los puntos dan $$$m$ residuales: necesita un indicador integral. Cuadramos cada residuo en un cuadrado y calculamos el promedio:

$$ $$MSE (a, b) = \ frac {1} {m} \ sum_ {i = 1} ^ {m} (z_ {i} - \ widehat {z_ {i}}) ^ 2$$

Esta medida de proximidad se denomina error cuadrático medio (en lo sucesivo denominado mse ):

 # r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss) 

 [Out]: 3868.2291666666665 

Al minimizar mse , resolvemos el problema de los mínimos cuadrados ( minimización de cuadrados no lineales ):

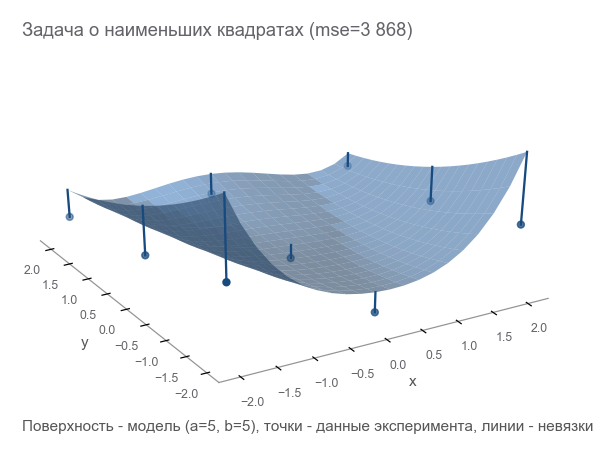
Se puede ver que los parámetros no adivinaron en absoluto.

Formulamos el problema en TensorFlow

El modelo tiene la forma $$$z = rosenbrock (x, y, a, b)$ . Lo traemos a la forma $$$y = f (x, p)$ (generalmente las matemáticas escriben $$$\ beta$ en lugar de $$$p$ pero los programadores no usan beta). Ahora el modelo tiene la forma $$$y = rosenbrock (x, p)$ donde $$$y$ - altura $$$x$ Es el vector de coordenadas de dos elementos (componente) y $$$p$ - vector de parámetros.

Los programadores a menudo piensan en los vectores como matrices unidimensionales. Esto no es del todo correcto. Una matriz de números es un medio de representar un vector. Puede representar un vector como una matriz de dimensión $$$N$ , matriz bidimensional $$$1 \ veces N$ e incluso una matriz $$$N \ por 1$ En los casos en que el hecho de que el vector sea un vector de columna (por ejemplo, para multiplicar una matriz por él) es importante:

$$ $$\ begin {bmatrix} x_1 \\\ vdots \\ x_N \ end {bmatrix}$$

TensorFlow utiliza el concepto de tensor . Un tensor , como una matriz, puede ser unidimensional (para representar un vector ), bidimensional (para un vector de matriz o columna ) y cualquier dimensión más grande.

 #    ('placeholder' ,    #      ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) #   ('variable' ,    ) #     (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) #  y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) #  r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2) 

El código de TensorFlow no es diferente en forma del código de Numpy. El contenido es enorme. El código Numpy calcula el valor mse. El código TensorFlow no realiza ningún cálculo en absoluto, forma un gráfico de flujo de datos que puede calcular . Un momento muy tolerante para el cerebro es el trabajo de la función rosenbrock . Lo usamos en ambos casos. Pero cuando pasamos las matrices de Numpy, realiza los cálculos de acuerdo con la fórmula y devuelve los números. Y cuando transferimos los tensores a TensorFlow, forma una subgrafía del flujo de datos y devuelve su borde en forma de tensor. Milagros de polimorfismo, pero no abuses de ellos:

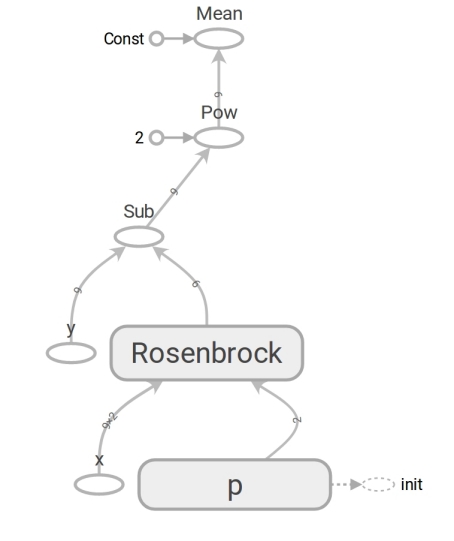
Gracias a la presencia de dicho gráfico de flujo de datos, TensorFlow en particular es capaz de calcular derivados automáticamente (utilizando la técnica de diferenciación automática en modo inverso ).

Un momento de matemática. Los bloques "para los que han olvidado" se esconderán en un spoiler.

Creamos un gráfico de flujo de datos, ejecutemos el cálculo de mse:

 #        #      placeholder (  ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} #       TensorFlow session = tf.Session() #     session.run(tf.global_variables_initializer()) #   ()  loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss) 

 [Out]: 3868.2291666666665 

El resultado es el mismo que con Numpy. Entonces no se equivocaron.

Comienza a optimizar

Desafortunadamente, no fue posible adivinar los parámetros. Pero luego nosotros:

1. Establecemos el criterio de optimización: el valor mínimo de mse.
2. Se determinaron parámetros variables: vector $$$p$ con componentes $$$a$ , $$$b$ Funciones de Rosenbrock.
3. Todavía no hemos pensado en las limitaciones, pero no están allí.

En el último paso, construimos un gráfico de flujo de datos con un tensor de pérdida finita ( función de pérdida ). El objetivo de la optimización es encontrar el valor del vector de parámetros $$$p$ en el cual el valor de la función de pérdida es mínimo. Tuvimos suerte, el gráfico de esta función es muy simple (cóncavo y sin mínimos locales):

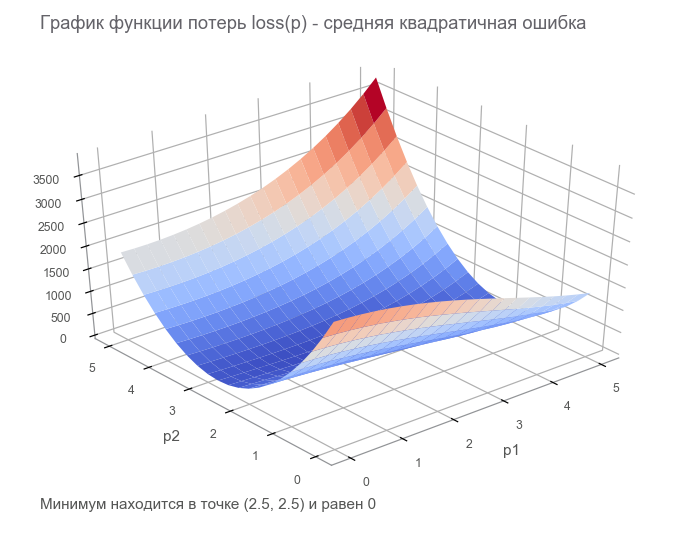
Comenzando con la optimización. Para comenzar, escribimos un ciclo generalizado:

 # :   mse,   ,  #   mse,        placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) #           while current_loss > target_loss and step < max_steps: step += 1 #    1, 2, 4, 8, 16...  if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') #    session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') 

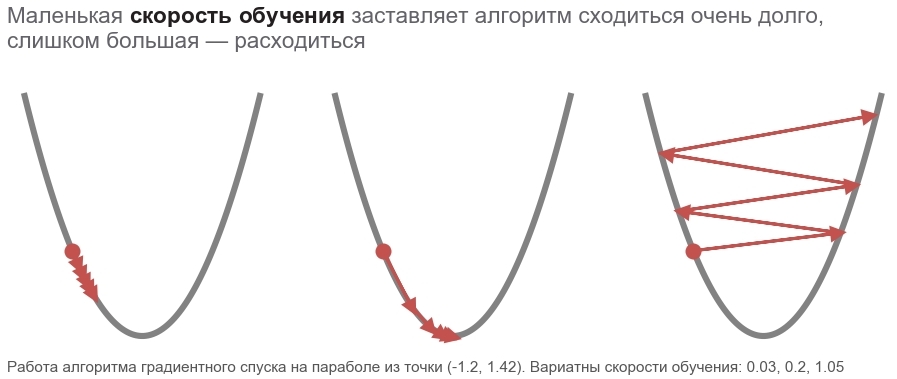
Optimizamos por el método del descenso de gradiente más rápido (SGD)

Las acciones de este método se pueden comparar con montar un esquiador atrevido, que siempre baja la pendiente (en la dirección más empinada). En este caso, solo se tiene en cuenta la pendiente en el punto de ubicación. Y si la pendiente es fuerte, el esquiador vuela una gran distancia antes del próximo cambio. Con una pendiente débil, se mueve en pequeños pasos. Tal vez como volar en un árbol (el algoritmo diverge ) y queda atrapado en un pozo ( mínimo local ).

Puedes escribir de la siguiente manera (cambiar $$$\ boldsymbol {p}$ en $$$\ boldsymbol {p} - ...$ ):

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - \ alpha [\ nabla_ {p} loss (\ boldsymbol {p})]$$

Grasiento $$$\ boldsymbol {p}$ enfatiza que este es el punto de ubicación real: el valor del vector de parámetros en el paso actual. En el primer paso, esta es nuestra suposición (5, 5). Hay dos puntos interesantes en la fórmula: $$$\ alpha$ - tasa de aprendizaje ( tasa de aprendizaje ), $$$\ nabla_ {p} pérdida$ - gradiente ( gradiente ) de la función de pérdida por el vector de parámetros.

 #        grad = tf.gradients(loss, p)[0] #   learning_rate = 0.0005 #   ,     apply_gradients - #         opt = tf.train.GradientDescentOptimizer(learning_rate=1) #           sgd = opt.apply_gradients([(learning_rate*grad, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959] 

Tomó 582 pasos:

Optimizamos por el método de Adam

No iremos más allá en los métodos de gradiente, pero hay muchas variaciones. Puede leer sobre ellos en el artículo Métodos para optimizar las redes neuronales . En TensorFlow, muchos optimizadores ya están implementados. Por ejemplo, Adam:

 #       , #      adm = tf.train.AdamOptimizer(15).minimize(loss) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008] 

Gestionado en 317 pasos. Mucho más rápido

Optimizamos por el método de Newton

Las acciones de los métodos de segundo orden se pueden comparar a montar en un snowboardista racional de freeride que reflexiona sobre el siguiente punto de su ruta durante mucho tiempo y tiene en cuenta no solo la pendiente en el lugar, sino también la curvatura.

De hecho, tanto los métodos de descenso de gradiente como los métodos de segundo orden intentan adivinar ( aproximar ) la función en el punto actual. Los métodos de gradiente se centran solo en la pendiente de la gráfica de la función en el punto, la primera derivada. Los métodos de segundo orden, además del sesgo, tienen en cuenta la curvatura , la segunda derivada: "si la curvatura persiste, ¿dónde estará el mínimo?" Calculamos y vamos allí:

Para construir tal aproximación y calcular el punto mínimo estimado, puede usar la serie Taylor . Para el caso unidimensional, la aproximación por un polinomio de segundo orden en el punto $$$a$ se ve así:

$$ $$f (x) \ aprox f (a) + \ frac {f '(a) (x-a)} {1!} + \ frac {f' '(a) (x-a) ^ 2} {2!}$$

El mínimo se alcanza a las $$$x = a - \ frac {f '(a)} {f' '(a)}$ . El caso multidimensional parece más serio:

Aproximación por un polinomio de segundo orden para una función de un vector a través de un gradiente y una matriz de Hesse en un punto $$$a$ se ve así:

$$ $$f (x) \ aprox. f (a) + (xa) ^ \ intercal [\ nabla_ {x} f (a)] + \ frac {1} {2!} (xa) ^ \ intercal [\ boldsymbol {H } f_ {x} (a)] (xa)$$

El mínimo se alcanza a las $$$x = a - [\ boldsymbol {H} f_ {x} (a)] ^ {- 1} [\ nabla_ {x} f (a)]$ . La forma casi coincide con el caso unidimensional: reemplazamos la primera derivada con un gradiente, la segunda con una matriz de Hesse e hicimos una corrección para trabajar con vectores. Es imposible dividir un vector por una matriz, por lo tanto, se usa la multiplicación por la matriz inversa . T significa transposición . La fórmula implica que, por defecto, un vector es una columna. Transponer convierte un vector de columna en un vector de fila . Al implementar en TensorFlow, esto debe tenerse en cuenta, pero en la dirección opuesta: por defecto, el vector es una cadena (tensor unidimensional). Por si acaso: la transposición no es una rotación de 90 grados, es la transformación de filas en columnas en el mismo orden.

Entonces, el paso del método Newton tiene la siguiente forma:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {H} loss_ {p} (\ boldsymbol {p})] ^ {- 1} [\ nabla_ {p} pérdida (\ boldsymbol {p} )]$$

TensorFlow tiene todo para implementar este método:

 #        hess = tf.hessians(loss, p)[0] #    - grad_col = tf.expand_dims(grad, -1) # ,      dp = tf.matmul(tf.linalg.inv(hess), grad_col) #  -  - dp = tf.squeeze(dp) #  p  dp    newton = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p)) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5] 

Suficientes 6 pasos:

Optimizado por el algoritmo de Gauss-Newton

El método de Newton tiene un inconveniente: la matriz de Hesse. Gracias a TensorFlow podemos contarlo en una línea de código. Según la wiki, Johann Karl Friedrich Gauss hizo la primera mención de su método en 1809. El cálculo de la matriz de Hesse para varios parámetros para el método de mínimos cuadrados podría llevar mucho tiempo. Ahora podemos suponer que el algoritmo de Gauss-Newton usa la aproximación de la matriz de Hesse a través de la matriz de Jacobi para simplificar los cálculos. Pero desde el punto de vista de la historia, esto no es así: Ludwig Otto Hesse (quien desarrolló la matriz que lleva su nombre) nació en 1811, 2 años después de la primera mención del algoritmo. Y Carl Gustav Jacobi tenía 5 años.

El algoritmo de Gauss-Newton no funciona con la función de pérdida. Funciona con la función residual. $$$r (p)$ . Esta función toma un vector de entrada de parámetros $$$p$ y devuelve un vector de residuos . En nuestro caso, el vector $$$p$ consta de 2 componentes (parámetros $$$a$ y $$$b$ Funciones de Rosenbrock) y el vector residual de $$$m$ componente (según el número de experimentos). Se obtiene la función vectorial del argumento vector. Su derivada:

Para no confundirse con la abundancia de personajes, asumimos que $$$\ boldsymbol {J} _ {r}$ - Matriz de funciones residuales de Jacobi en el punto actual $$$\ boldsymbol {p}$ . Entonces el algoritmo de Gauss-Newton se puede escribir de la siguiente manera:

$$ $$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}] ^ {- 1} \ boldsymbol {J} _ {r } ^ \ intercal r (\ boldsymbol {p})$$

La grabación en la forma coincide completamente con la grabación del método de Newton. Solo en lugar de la matriz de Hesse se usa $$$\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}$ en lugar del gradiente $$$\ boldsymbol {J} _ {r} ^ \ intercal r (\ boldsymbol {p})$ . A continuación, veremos por qué se puede usar tal aproximación. Mientras tanto, procedamos a la implementación en TensorFlow:

 #  ,  TensorFlow     , #   ,        #  .  ,   : # 1)       tf.unstack(r) # 2)      tf.gradients(r_i, p) # 3)       tf.stack #      ,     #       j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) #     - r_col = tf.expand_dims(r, -1) #      hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # ,      dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) #  -  - dp = tf.squeeze(dp) #  p  dp    ng = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict) 

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5] 

Suficientes 4 pasos. Menos que para el método de Newton.

Como se puede ver en el código, la función de pérdida no se usa en la optimización, solo para detener y registrar criterios. ¿Cómo sabe el algoritmo de optimización qué función minimizar? La respuesta es sorprendente: ¡de ninguna manera! Gauss-Newton minimiza solo el error cuadrático medio .

Repara la parte matemática del artículo

Repetimos todas las matemáticas que necesitábamos. Arreglemos un poco para enfocarnos más en la programación y TensorFlow. Es posible que necesite un lápiz para trazar la secuencia de acciones matemáticas.

Hay un modelo $$$y = f (x, p)$ donde $$$x$ - vector $$$p$ - vector de parámetros de dimensión $$$n$ y $$$y$ - escalar De los experimentos recibidos $$$m$ puntos $$$(x_ {1}, y_ {1}), ..., (x_ {m}, y_ {m})$ ( pares de datos ). La función residual del vector depende solo del vector de parámetros: $$$r (p) = (r_ {1} (p), ... r_ {m} (p))$ donde $$$r_ {k} (p) = y_ {k} - \ widehat {y_ {k}} = y_ {k} - f (x_ {k}, p)$ . , $$$p$ , $$$x_{k}, y_{k}$ ? , $$$x_{k}, y_{k}$ , .

$$$p$ , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , $$$m$ . . :

$$ $$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$$

$$$p$ $$$(p)$ .

, . — . — , $$$r^2$ $$$2r \frac{\partial r}{\partial p}$ . :

$$ $$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}})$$

. :

$$ $$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$$

. , , $$${(uv)}'={u}'v+u{v}'$.
Genial .

, , , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$. , , $$$r_{k}$, . — . , ? -.

:

$$ $$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$$

, , . Tenga en cuenta que:

$$ $$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$$

"" . ( ). , — $$$2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$, .
( ):

$$ $$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$$

, , - — , mse .

. , , . $$$m$$$$(x_{1}, y_{1}), ..., (x_{m}, y_{m})$, $$$y = rosenbrock(x, p)$. $$$p$, .

, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .

( multi-layer perceptron neural network mlp ). , , :

• ( starting values ) . Xavier'a, .
• ( overfitting ). — . , . — .
• ( scaling of the input ). , .

9 . 500:

 #    def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting   ,      validation_data_points = get_random_rosenbrock_data_points(m) 

500 . — ( learner ), ( outcome measurement ) ( features ) .

( network diagram ). MatLab:

( input ). $$$W$( weights ) 2x10, $$$b$( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).

, , ( $$$tanh$):

$$ $$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix}$$

:

$$ $$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2$$

. $$$W_{1}$"" $$$h_{1}$, - $$$W_{2}$. 41 . , .

$$$m \times 2$, . - $$$\widehat{y}$de $$$m$:

 #     10 "" n_hidden = 10 #      Xavier'a initializer = tf.contrib.layers.xavier_initializer() #    x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) #         W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) #   ,  tanh   h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) #        W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) #   y_hat = tf.matmul(h1, W2) + b2 #  r = y - y_hat #   mse     loss = tf.reduce_mean(tf.square(r)) #      placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]} 

Adam

Adam $$$rosenbrock$. mse :

 #    adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) #   ,    40000  train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866 

. : , , .

$$$rosenbrock$2 . :

• . 9 , 500. .
• . - $$$p$, .

:

 #      y   x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] #  -   #      _, jacobian = tf.while_loop( lambda i, _: i < m, #           #   (-),   x     lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) #       return jacobian.stack() #       r_flat = tf.squeeze(r) #        #       parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) #           hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r) 

$$$\boldsymbol{J}r_{p}$. , 4 $$$W_1, b_1, W_2, b_2$. 4 $$$\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$tf.concat .

. tf.while_loop , $$$r_i$, , stack .

$$$r_i$$$$W_1$: $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$. tf.reshape (-1,) $$$\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$.

. - . — TensorFlow . — - - $$$W_1, b_1, W_2, b_2$. -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .

-

hess_approx grad_approx -. $$$rosenbrock$, . :

1. : $$$\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
2. :
   $$$\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $$$\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$, $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$, $$$\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$.
3. , :
   $$$\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$, $$$\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
4. .

 # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       gn = opt.apply_gradients(zip(dps, parms)) #   session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict) 

 [Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible. 

- . , . - , .

, .

-

. Matlab trainlm . . MathWorks.

- : $$$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$. - :

$$ $$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$$

$$$\ mu$$$$I$$$$n$( ). $$$\ mu$, -. , . , LM -.

:

 mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       lm = opt.apply_gradients(zip(dps, parms)) 

$$$\ mu$? LM - . , . , $$$\ mu$, . — , mse . , :

 #       store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] #  TensorFlow       save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] #   mu    3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) #    mse current_loss = session.run(loss, feed_dict) #    100   while current_loss > 1e-10 and step < 100: step += 1 #  1, 2, 4...   if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') #    session.run(save_parms) # ,     mse while True: #    session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: #  -  mu  10     feed_dict[mu] *= 10 session.run(restore_parms) else: #  -  mu  10     feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict))) 

 [Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034 

100 LM mse 10 , 40 .

. , . , rosenbrock_train.py .

2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .

:

$$ $$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$$

rosenbrock_train.py get_rand_rosenbrock_points .

-

- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :

1. 10 000 6D .
2. 3 12, 10, 8 (311 ).
3. .
4. 3.5 .

. - 2 . LM . 20 .

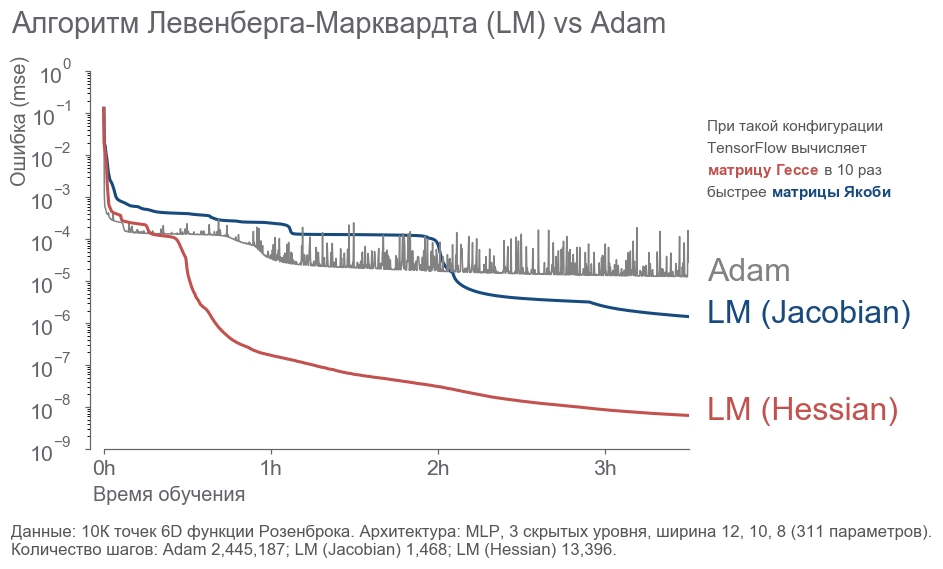
rosenbrock_train.py . . , .

Conclusión

, . " ", , . , . , 273 . - , .

, :

1. .
2. ( ) -:
   [1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
   [2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

, - . , . "".