Una de las tareas más importantes en el campo de la ciencia de datos no es solo la construcción de un modelo capaz de hacer predicciones de alta calidad, sino también la capacidad de interpretar tales predicciones.
Si no solo sabemos que el cliente está dispuesto a comprar un producto, sino que también entendemos qué influye en su compra, podremos construir una estrategia de la compañía en el futuro dirigida a mejorar la eficiencia de las ventas.
O el modelo predijo que el paciente enfermaría pronto. La precisión de tales predicciones no es muy alta, porque Hay muchos factores ocultos en el modelo, pero una explicación de las razones por las cuales el modelo hizo tal predicción puede ayudar al médico a prestar atención a los nuevos síntomas. Por lo tanto, es posible expandir los límites de aplicación del modelo si su precisión en sí misma no es demasiado alta.
En esta publicación quiero hablar sobre la técnica
SHAP , que le permite mirar bajo el capó de una variedad de modelos.
Si con los modelos lineales es cada vez menos claro, cuanto mayor sea el valor absoluto del coeficiente debajo del predictor, más importante es este predictor, entonces explicar la importancia de las características del mismo aumento de gradiente es mucho más difícil.
¿Por qué era necesaria una biblioteca así?

En la pila sklearn, en los paquetes xgboost, lightGBM, había métodos incorporados para evaluar la importancia de las características (importancia de las características) para los "modelos de madera":
- Ganar
Esta medida muestra la contribución relativa de cada característica al modelo. Para el cálculo, revisamos cada árbol, observamos cada nodo del árbol cuya característica conduce a la partición del nodo y cuánto disminuye la incertidumbre del modelo según la métrica (impureza de Gini, ganancia de información).
Para cada característica, se resume su contribución sobre todos los árboles.
- Cubierta
Muestra el número de observaciones para cada característica. Por ejemplo, tiene 4 características, 3 árboles. Suponga que la característica 1 en los nodos del árbol contiene 10, 5 y 2 observaciones en los árboles 1, 2 y 3, respectivamente. Luego, para esta característica, la importancia será 17 (10 + 5 + 2).
- Frecuencia
Muestra con qué frecuencia se produce esta característica en los nodos del árbol, es decir, se considera el número total de divisiones de árbol en nodos para cada característica en cada árbol.
El principal problema en todos estos enfoques es que no está claro cómo exactamente esta característica afecta la predicción del modelo. Por ejemplo, aprendimos que el nivel de ingresos es importante para evaluar la solvencia de un cliente bancario para pagar un préstamo. ¿Pero cómo exactamente? ¿Cuánto mayor sesgo de ingresos predicen los modelos?
Por supuesto, podemos hacer varias predicciones cambiando el nivel de ingresos. ¿Pero qué hacer con otras características? Después de todo, nos encontramos en una situación que necesitamos para comprender la influencia del ingreso
independientemente de otras características, con su valor promedio.
Hay una especie de cliente bancario promedio "en el vacío". ¿Cómo cambiarán las predicciones del modelo con los cambios en los ingresos?
Aquí la biblioteca
SHAP viene al rescate.
Calculamos la importancia de las características usando SHAP
En la biblioteca
SHAP , para evaluar la importancia de las
características, se calculan los valores de Shapley (por el nombre de un matemático estadounidense y se nombra la biblioteca).
Para evaluar la importancia de una característica, las predicciones del modelo se evalúan
con y
sin esta característica.
Un poco de prehistoria

Los significados de Shapley provienen de la teoría de juegos.
Considere el escenario: un grupo de personas juega a las cartas. ¿Cómo distribuir el fondo de premios entre ellos de acuerdo con su contribución?
Se hacen una serie de suposiciones:
- La cantidad de recompensa para cada jugador es igual al premio total
- Si dos jugadores hacen una contribución igual al juego, reciben una recompensa igual.
- Si un jugador no ha hecho ninguna contribución, no recibe una recompensa.
- Si un jugador ha gastado dos juegos, su recompensa total consiste en la cantidad de recompensas para cada uno de los juegos.
Presentamos las características del modelo como jugadores, y el premio acumulado como la predicción final del modelo.
Veamos un ejemplo.
La fórmula para calcular el valor de Shapley para la característica i-ésima:
$$ display $$ \ begin {ecation *} \ phi_ {i} (p) = \ sum_ {S \ subseteq N / \ {i \}} \ frac {| S |! (n - | S | -1) !} {n!} (p (S \ cup \ {i \}) - p (S)) \ end {ecuación *} $$ display $$
Aquí:
p (S \ cup \ {i \}) Es una predicción de un modelo con la característica i-ésima,
p(S) - esta es una predicción del modelo sin la función i-th,
n - número de características,
S - un conjunto arbitrario de características sin la característica i-ésima
El valor de Shapley para la característica i-ésima se calcula para cada muestra de datos (por ejemplo, para cada cliente de la muestra) en todas las combinaciones posibles de características (incluida la ausencia de todas las características), luego se suman los valores obtenidos módulo y se obtiene la importancia final de la característica i-ésima.
Estos cálculos son extremadamente caros, por lo tanto, debajo del capó, se utilizan varios algoritmos para optimizar los cálculos, para más detalles, consulte el enlace de arriba en el github.
Tome el ejemplo de vainilla de la
documentación de xgboost .
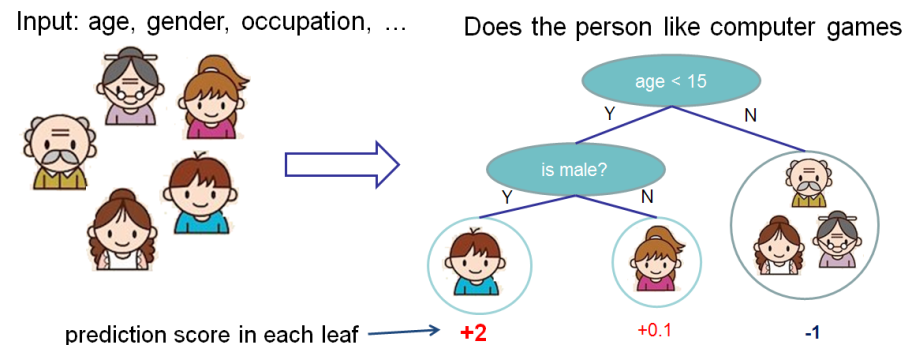
Queremos evaluar la importancia de las funciones para predecir si a una persona le gustan los juegos de computadora.
En este ejemplo, por simplicidad, tenemos dos características: edad (edad) y género (género). El género (género) toma los valores 0 y 1.
Tome Bobby (el niño pequeño en el nodo más a la izquierda del árbol) y calcule el valor de Shapley para la edad característica (edad).
Tenemos dos conjuntos de características S:
\ {\} - sin características
\ {gender \} - Solo hay una característica de género.
La situación cuando no hay valores de características
Los diferentes modelos funcionan de manera diferente con situaciones en las que no hay características para la muestra de datos, es decir, para todas las características, los valores son NULL.
En este caso, considerará que el modelo promedia las predicciones sobre las ramas de los árboles, es decir, la predicción sin características será
[(2+0.1)/2+(−1)]/2=0.025 .
Si agregamos conocimiento de la edad, entonces la predicción del modelo será
(2+0.1)/2=1.05 .
Como resultado, el valor de Shapley para el caso de la ausencia de características:
\ frac {| S |! (n - | S | -1)!} {n!} (p (S \ cup \ {i \}) - p (S)) = \ frac {1 (2-0 -1)!} {2!} (1.025) = 0.5125
La situación cuando conocemos el género
Para bobby para
gender predicción sin características de edad, solo con características de género es igual
[(2+0.1)/2+(−1)]/2=0.025 . Si conocemos la edad, entonces la predicción es el árbol más a la izquierda, es decir, 2.
Como resultado, el valor de Shapley para este caso:
$$ display $$ \ begin {ecation *} \ frac {| S |! (n - | S | -1)!} {n!} (p (S \ cup \ {i \}) - p (S) ) = \ frac {1 (2-1-1)!} {2!} (1.975) = 0.9875 \ end {ecuación *} $$ display $$
Resumir
El valor total de Shapley para las características age (age):
$$ display $$ \ begin {ecation *} \ phi_ {Age Bobby} = 0.9875 + 0.5125 = 1.5 \ end {ecation *} $$ display $$
Un verdadero ejemplo de negocios
La biblioteca SHAP tiene una rica funcionalidad de visualización que ayuda a explicar fácil y simplemente el modelo tanto para el negocio como para el analista mismo, a fin de evaluar la idoneidad del modelo.
En uno de los proyectos, analicé la salida de empleados de la empresa. Como modelo, se utilizó xgboost.
Código en python:
import shap shap_test = shap.TreeExplainer(best_model).shap_values(df) shap.summary_plot(shap_test, df, max_display=25, auto_size_plot=True)
El gráfico resultante de la importancia de las características:
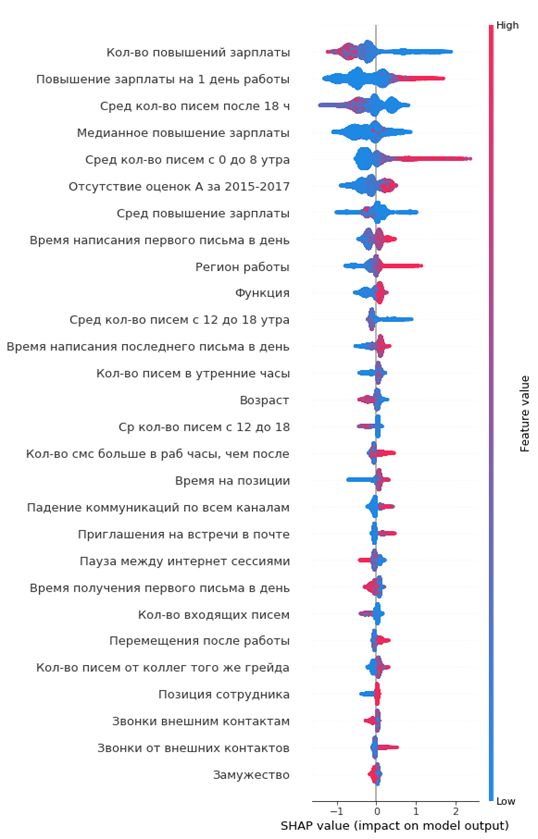
Cómo leerlo:
- los valores a la izquierda de la línea vertical central son la clase negativa (0), a la derecha - positiva (1)
- cuanto más gruesa es la línea en el gráfico, más puntos de observación
- cuanto más rojos son los puntos en el gráfico, mayor es el valor de las características en él
Del gráfico, puede sacar conclusiones interesantes y verificar su adecuación:
- cuanto menor sea el aumento salarial del empleado, mayor será la probabilidad de su partida
- hay regiones de oficinas donde el flujo de salida es mayor
- cuanto más joven es el empleado, mayor es la probabilidad de su partida
- ...
Puede formarse inmediatamente un retrato del empleado saliente: ella no recibió un aumento salarial, era lo suficientemente joven, soltero, durante mucho tiempo en el mismo puesto, no hubo aumentos de calificaciones, no hubo altas calificaciones anuales, comenzó a comunicarse poco con sus colegas.
Simple y conveniente!
Puede explicar la predicción para un empleado específico:

O vea la dependencia de las predicciones en una característica específica en forma de un gráfico 2D:
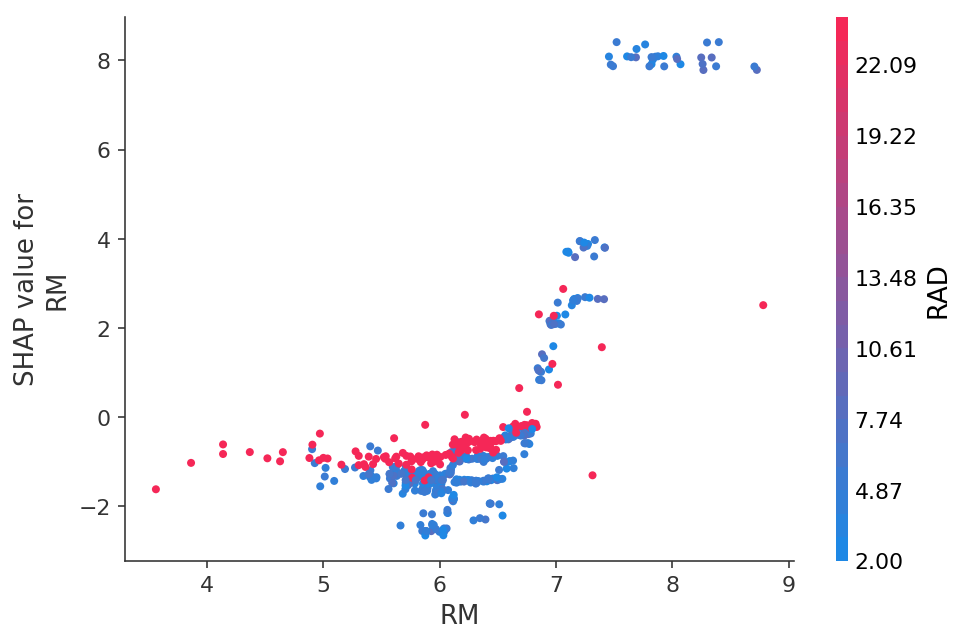
Incluso puede visualizar las predicciones de las redes neuronales en imágenes:

Conclusión
Yo mismo aprendí acerca de los valores SHAP hace unos seis meses y esto reemplazó por completo a otros métodos para evaluar la importancia de las características.
Las principales ventajas:
- visualización e interpretación convenientes
- Cálculo honesto de la importancia de las características
- La capacidad de evaluar características para una submuestra particular de datos (por ejemplo, cómo nuestros clientes difieren de otros clientes en la muestra) se realiza mediante un filtro simple del conjunto de datos en pandas y su análisis en shap, literalmente un par de líneas de código