Les presento la traducción de un capítulo del libro Ciencia práctica de datos con Anaconda.
"Análisis de datos predictivos: modelado y validación"
Nuestro objetivo principal al realizar diversos análisis de datos es buscar patrones para predecir lo que puede suceder en el futuro. Para el mercado de valores, los investigadores y expertos realizan varias pruebas para comprender los mecanismos del mercado. En este caso, puede hacer muchas preguntas. ¿Cuál será el nivel del índice del mercado en los próximos cinco años? ¿Cuál será el próximo rango de precios para IBM? ¿La volatilidad del mercado aumentará o disminuirá en el futuro? ¿Cuál podría ser el efecto si los gobiernos cambian sus políticas fiscales? ¿Cuáles son las posibles ganancias y pérdidas si un país comienza una guerra comercial con otro? ¿Cómo predecimos el comportamiento del consumidor analizando algunas variables relacionadas? ¿Podemos predecir la probabilidad de que un estudiante graduado se gradúe con éxito? ¿Podemos encontrar una conexión entre el comportamiento específico de una enfermedad en particular?
Por lo tanto, consideraremos los siguientes temas:
- Comprender el análisis predictivo de datos
- Conjuntos de datos útiles
- Pronosticar eventos futuros
- Selección de modelo
- Prueba de causalidad de Granger
Comprender el análisis predictivo de datos
Las personas pueden tener muchas preguntas sobre eventos futuros.
- Un inversor, si puede predecir el movimiento futuro de los precios de las acciones, puede obtener grandes ganancias.
- Las empresas, si pudieran predecir la tendencia de sus productos, podrían aumentar el precio de sus acciones y su participación en el mercado.
- Los gobiernos, si pudieran predecir el impacto del envejecimiento de la población en la sociedad y la economía, tendrían más incentivos para desarrollar mejores políticas en términos del presupuesto estatal y otras decisiones estratégicas relevantes.
- Las universidades, si pudieran comprender bien la demanda del mercado en términos de calidad y conjunto de habilidades para sus graduados, podrían desarrollar un conjunto de mejores programas o lanzar nuevos programas para satisfacer las necesidades futuras de la fuerza laboral.
Para un mejor pronóstico, los investigadores deberían considerar muchas preguntas. Por ejemplo, ¿los datos de la muestra son demasiado pequeños? ¿Cómo eliminar las variables que faltan? ¿Este conjunto de datos está sesgado en términos de procedimientos de recopilación de datos? ¿Cómo nos sentimos acerca de los extremos o las emisiones? ¿Qué es la estacionalidad y cómo la tratamos? ¿Qué modelos debemos usar? Este capítulo abordará algunos de estos problemas. Comencemos con un conjunto de datos útil.
Conjuntos de datos útiles
Una de las mejores fuentes de datos es el
Depósito de aprendizaje automático UCI . Después de visitar el sitio, veremos la siguiente lista:

Por ejemplo, si selecciona el primer conjunto de datos (Abulón), veremos lo siguiente. Para ahorrar espacio, solo se muestra la parte superior:

Desde aquí, los usuarios pueden descargar el conjunto de datos y encontrar definiciones de variables. El siguiente código se puede usar para cargar un conjunto de datos:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
La salida correspondiente se muestra aquí:

De la conclusión anterior, sabemos que en el conjunto de datos hay 427 observaciones (conjuntos de datos). Para cada uno de ellos, tenemos 7 funciones relacionadas, como
Nombre, Tipos de datos, Tarea predeterminada, Tipos de atributos, N_Instancias (número de instancias),
N_Attributes (número de atributos) y
Año . Una variable llamada
Default_Task puede interpretarse como el uso principal de cada conjunto de datos. Por ejemplo, un primer conjunto de datos llamado
Abalone se puede utilizar para la
Clasificación . La función
unique () se puede utilizar para buscar todas las posibles
Default_Task que se muestran aquí:
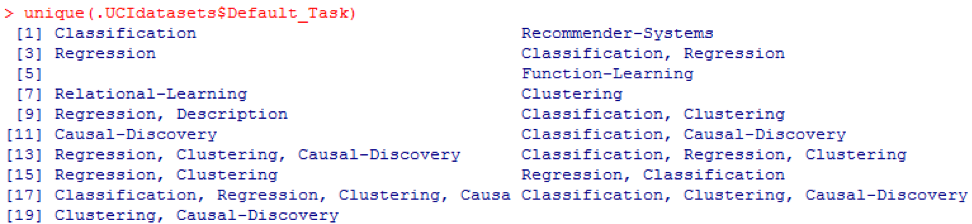
Paquete R AppliedPredictiveModeling
Este paquete incluye muchos conjuntos de datos útiles que se pueden usar para este capítulo y otros. La forma más fácil de encontrar estos conjuntos de datos es con la función de
ayuda () que se muestra aquí:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
Aquí mostramos algunos ejemplos de carga de estos conjuntos de datos. Para cargar un conjunto de datos, utilizamos la función
data () . Para el primer conjunto de datos llamado
abulón , tenemos el siguiente código:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
El resultado es el siguiente:

A veces, un conjunto de datos grande incluye varios conjuntos de subdatos:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
Para cargar cada conjunto de datos, podríamos usar las funciones
dim () ,
head () ,
tail () y
summary () .
Análisis de series temporales
Las series de tiempo pueden definirse como un conjunto de valores obtenidos en momentos consecutivos de tiempo, a menudo con intervalos iguales entre ellos. Hay diferentes períodos, como anual, trimestral, mensual, semanal y diario. Para las series temporales del PIB (producto interno bruto) usualmente usamos trimestralmente o anualmente. Para cotizaciones - frecuencias anuales, mensuales y diarias. Con el siguiente código, podemos obtener datos del PIB de EE. UU. Tanto trimestralmente como durante un período anual:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
Sin embargo, tenemos muchas preguntas para el análisis de series de tiempo. Por ejemplo, desde el punto de vista de la macroeconomía, tenemos ciclos económicos o comerciales. Las industrias o empresas pueden tener estacionalidad. Por ejemplo, utilizando la industria agrícola, los agricultores gastarán más en las temporadas de primavera y otoño y menos en el invierno. Para los minoristas, tendrían una gran afluencia de dinero al final del año.
Para manipular series temporales, podríamos usar las muchas funciones útiles incluidas en el paquete R, llamadas
timeSeries . En el ejemplo, tomamos los datos promedio diarios con una frecuencia semanal:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
También podríamos usar la función
head () para ver algunas observaciones:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
Pronosticar eventos futuros
Hay muchos métodos que podríamos usar al intentar predecir el futuro, como el promedio móvil, la regresión, la autorregresión, etc. Primero, comencemos con el más simple para el promedio móvil:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
En el código anterior, el valor predeterminado para el número de períodos es 10. Podríamos usar un conjunto de datos llamado MSFT incluido en el paquete R llamado
timeSeries (consulte el siguiente código):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
En modo manual, encontramos que el promedio de los primeros tres valores de
x coincide con el tercer valor de
y . En cierto modo, podríamos usar un promedio móvil para predecir el futuro.
En el siguiente ejemplo, mostraremos cómo evaluar los rendimientos esperados del mercado el próximo año. Aquí usamos el índice S & P500 y el valor promedio histórico anual como nuestros valores esperados. Los primeros comandos se usan para cargar un conjunto de datos relacionado llamado
.sp500monthly . El propósito del programa es evaluar el promedio anual promedio y el intervalo de confianza del 90 por ciento:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
Como puede ver en los resultados, el rendimiento anual promedio histórico para el S & P500 es del 9%. Pero no podemos decir que la rentabilidad del índice el próximo año será del 9%, porque puede ser del 5% al 13%, y estas son grandes fluctuaciones.
Estacionalidad
En el siguiente ejemplo, mostramos el uso de autocorrelación. Primero, descargamos un paquete R llamado
astsa , que significa análisis estadístico de series de tiempo aplicado. Luego cargamos el PIB de EE. UU. Con una frecuencia trimestral:
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
En el código anterior, la función
diff () acepta la diferencia, por ejemplo, el valor actual menos el valor anterior. Un segundo valor de entrada indica un retraso. Una función llamada
acf2 () se usa para construir e imprimir las series de tiempo ACF y PACF. ACF significa función de autocovarianza, y PACF significa función de autocorrelación parcial. Los gráficos relevantes se muestran aquí:
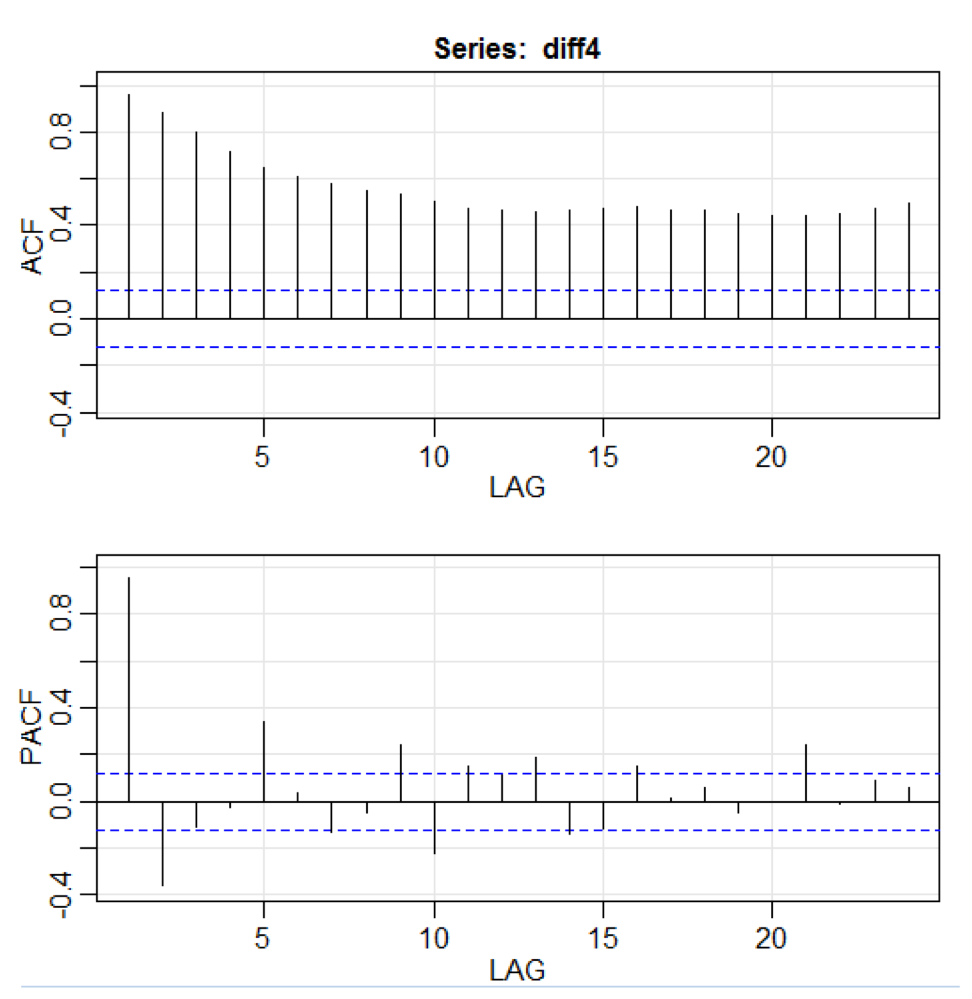
Visualización de componentes
Claramente, los conceptos y los conjuntos de datos serían mucho más comprensibles si pudiéramos usar gráficos. El primer ejemplo muestra fluctuaciones en el PIB de EE. UU. Durante las últimas cinco décadas:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
El horario correspondiente se muestra aquí:
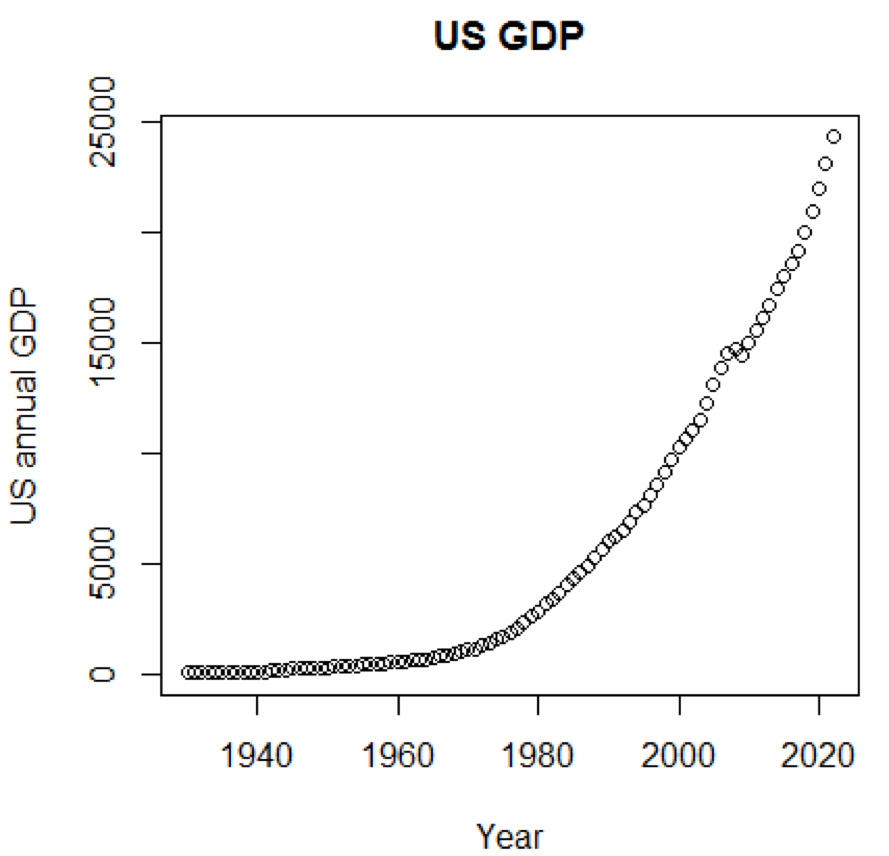
Si usáramos la escala logarítmica para el PIB, tendríamos el siguiente código y gráfico:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
El siguiente cuadro está cerca de una línea recta:
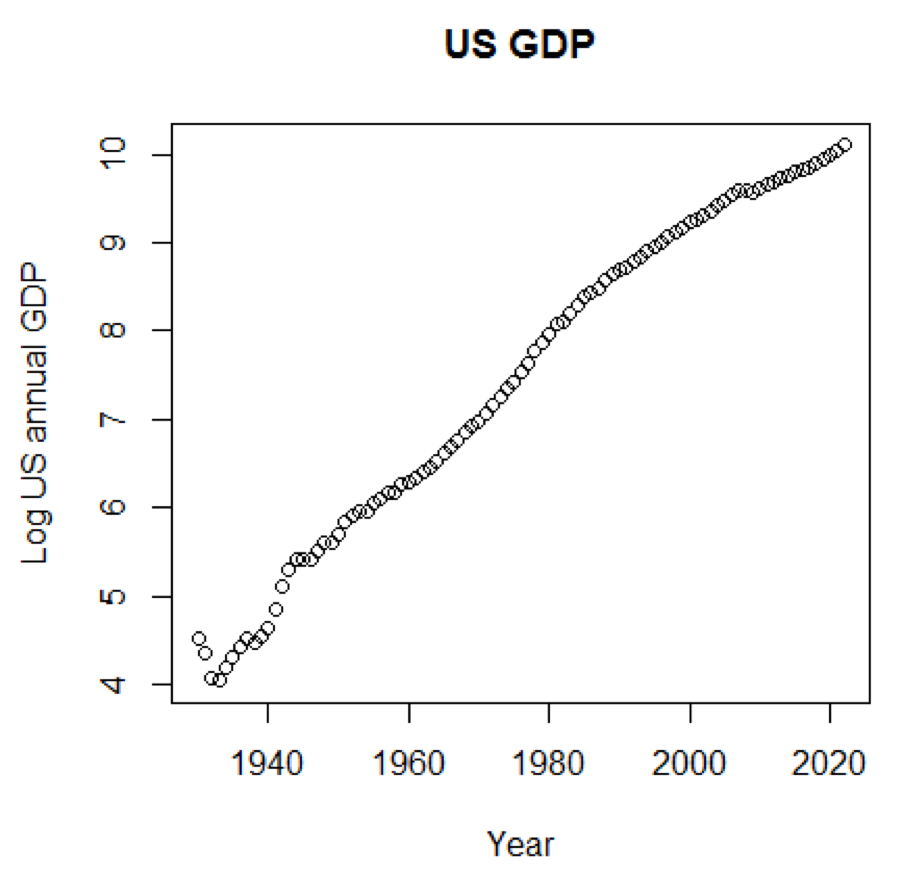
Paquete R - LiblineaR
Este paquete es un modelo predictivo lineal basado en la biblioteca LIBLINEAR C / C ++. Aquí hay un ejemplo del uso del conjunto de datos de
iris . El programa intenta predecir a qué categoría pertenece una planta utilizando datos de capacitación:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
La conclusión es la siguiente. BCR es una tasa de clasificación equilibrada. Para esta apuesta, cuanto mayor sea, mejor:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
Paquete R - eclust
Este paquete es una agrupación de orientación media para modelos predictivos interpretados en datos de alta dimensión. Primero, veamos un conjunto de datos llamado
simdata que contiene datos simulados para un paquete:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
La conclusión anterior muestra que la dimensión de los datos es de 100 por 502.
Y es el vector de respuesta continua y
E es la variable de entorno binario para el método ECLUST.
E = 0 para no expuesto (n = 50) y
E = 1 para expuesto (n = 50).
El siguiente programa R evalúa la transformación z de Fisher:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
Definimos la transformación z de Fisher. Suponiendo que tenemos un conjunto de
n pares
x i e
y i , podríamos estimar su correlación usando la siguiente fórmula:
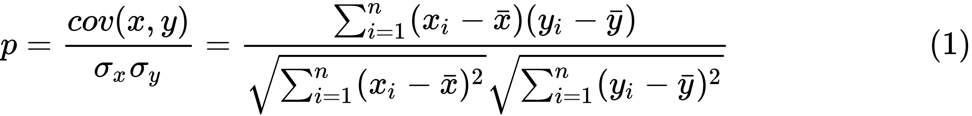
Aquí
p es la correlación entre dos variables, y

y
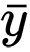
son medias de muestra para variables aleatorias
x e
y . El valor de
z se define como:
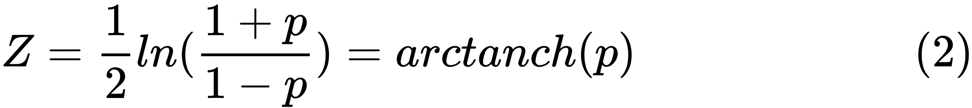 ln
ln es la función de logaritmo natural, y
arctanh () es la función tangente hiperbólica inversa.
Selección de modelo
Al encontrar un buen modelo, a veces nos enfrentamos a una falta / exceso de datos. El siguiente ejemplo está tomado
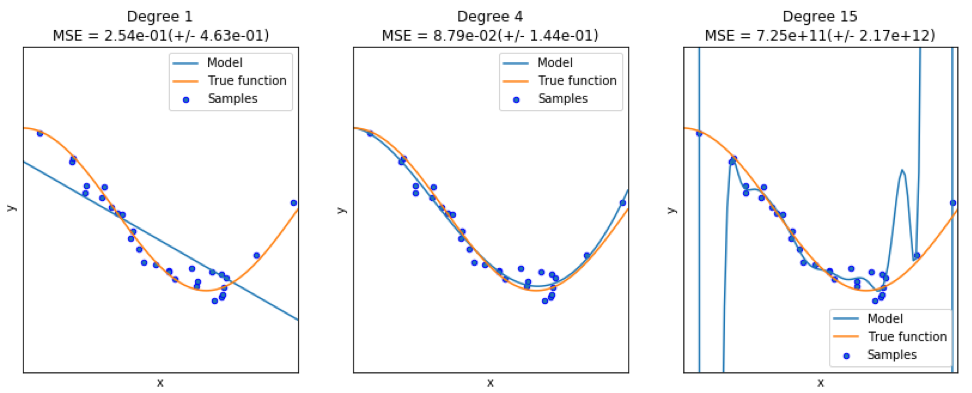
de aquí . Él demuestra los problemas de trabajar con esto y cómo podemos usar la regresión lineal con características polinómicas para aproximar funciones no lineales. Función especificada
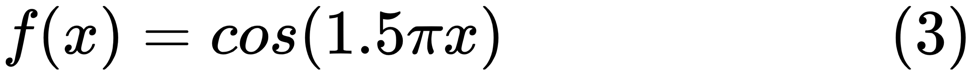
En el siguiente programa, intentamos usar modelos lineales y polinomiales para aproximar una ecuación. Aquí se muestra un código ligeramente modificado. El programa ilustra el efecto de la escasez / sobreoferta de datos en el modelo:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
Los gráficos resultantes se muestran aquí:
Paquete Python - modelo-pasarela
Un ejemplo se puede encontrar
aquí .
Las primeras líneas de código se muestran aquí:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
La conclusión correspondiente se muestra aquí. Para ahorrar espacio, solo se presenta la parte superior:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Paquete Python - sklearn
Dado que
sklearn es un paquete muy útil, vale la pena mostrar más ejemplos del uso de este paquete. El ejemplo dado aquí muestra cómo usar el paquete para clasificar documentos por tema usando el enfoque de la bolsa de palabras.
Este ejemplo usa la matriz
scipy.sparse para almacenar objetos y muestra varios clasificadores que pueden procesar eficientemente matrices dispersas. Este ejemplo utiliza un conjunto de datos de 20 grupos de noticias. Se descargará automáticamente y luego se almacenará en caché. El archivo zip contiene archivos de entrada y se puede descargar
aquí . El código está disponible
aquí . Para ahorrar espacio, solo se muestran las primeras líneas:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
La salida correspondiente se muestra aquí:
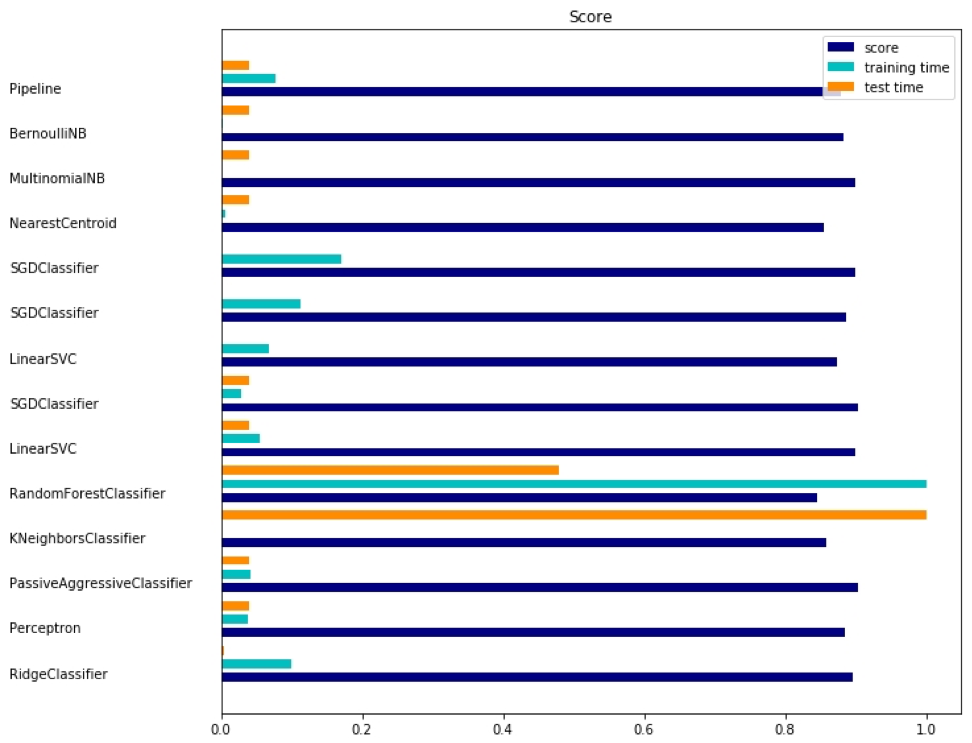
Hay tres indicadores para cada método: evaluación, tiempo de capacitación y tiempo de prueba.
Paquete Julia - QuantEcon
Tomemos, por ejemplo, el uso de cadenas de Markov:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
Resultado:
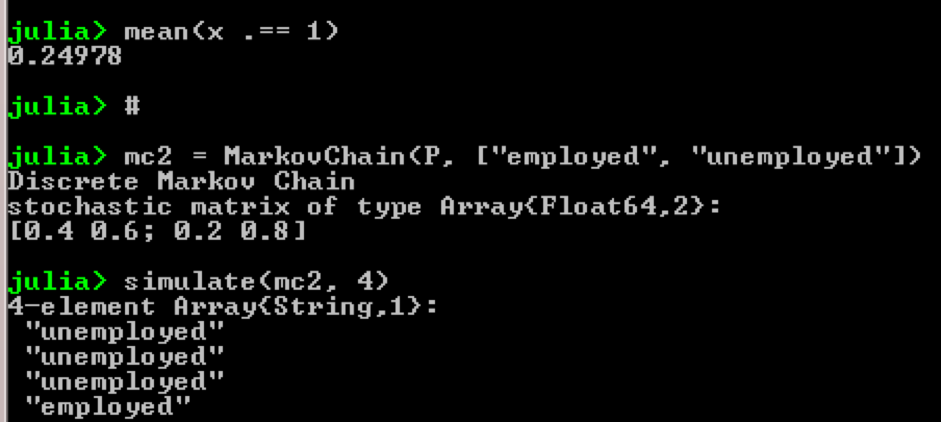
El propósito del ejemplo es ver cómo una persona de un estado económico en el futuro se transforma en otro. Primero, veamos el siguiente cuadro:
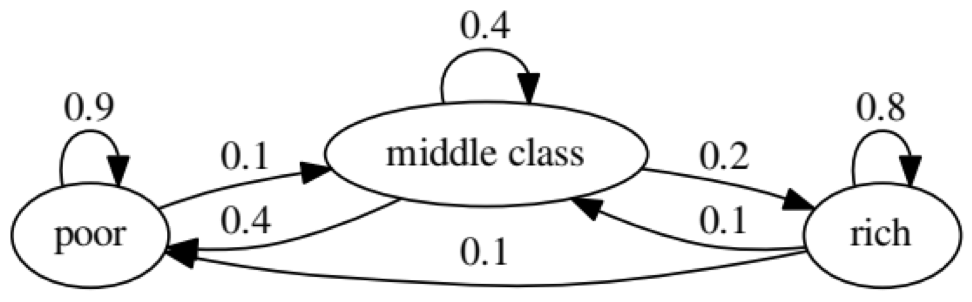
Miremos el óvalo más a la izquierda con el estado "pobre". 0.9 significa que una persona con este estado tiene un 90% de posibilidades de seguir siendo pobre, y el 10% ingresa a la clase media. Se puede representar mediante la siguiente matriz, los ceros son donde no hay borde entre los nodos:
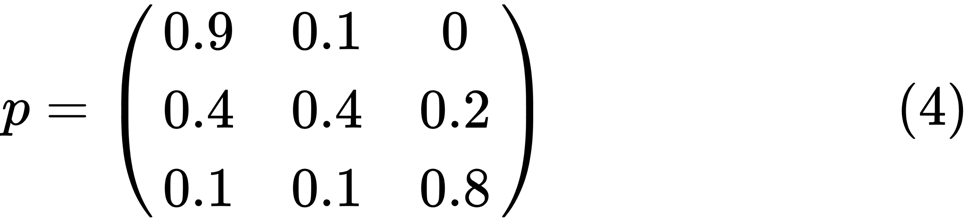
Se dice que dos estados, x e y, están relacionados entre sí si hay enteros positivos j y k, como:

Una cadena de Markov
P se llama irreducible si todos los estados están conectados; es decir, si
x e
y se informan para cada uno (x, y). El siguiente código confirmará esto:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
El siguiente gráfico representa un caso extremo, ya que el estado futuro de una persona pobre será 100% pobre:

El siguiente código también confirmará esto, ya que el resultado será
falso :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
Prueba de causalidad de Granger
La prueba de causalidad Granger se utiliza para determinar si una serie de tiempo es un factor y proporciona información útil para predecir la segunda. El siguiente código utiliza un
conjunto de datos llamado
ChickEgg como ilustración. El conjunto de datos tiene dos columnas, la cantidad de pollos y la cantidad de huevos, con una marca de tiempo:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
La pregunta es, ¿podemos usar la cantidad de huevos este año para predecir la cantidad de pollos el próximo año?
Si es así, entonces la cantidad de pollos será la razón Granger para la cantidad de huevos. Si este no es el caso, decimos que la cantidad de pollos no es una razón Granger para la cantidad de huevos. Aquí está el código relevante:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
En el modelo 1, tratamos de usar los retrasos de los pollitos más los retrasos de los huevos para explicar la cantidad de pollitos.
Porque el valor de
P es bastante pequeño (es significativo en 0.01), decimos que el número de huevos es la razón de Granger para el número de pollos.
La siguiente prueba muestra que los datos sobre pollos no pueden usarse para predecir el siguiente período:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
En el siguiente ejemplo, verificamos la rentabilidad de IBM y el S & P500 para descubrir que son motivo de Granger para otro.
Primero, definimos la función de rendimiento:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
Ahora se puede llamar a la función con valores de entrada. El objetivo del programa es probar si podemos usar los retrasos del mercado para explicar la rentabilidad de IBM. Del mismo modo, verificamos la explicación del retraso de IBM en los ingresos del mercado:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Los resultados muestran que el S & P500 se puede utilizar para explicar la rentabilidad de IBM para el próximo período, ya que es estadísticamente significativo al 0.1%. El siguiente código verificará si el retraso de IBM explica el cambio en el S & P500:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
El resultado sugiere que durante este período, los rendimientos de IBM pueden usarse para explicar el índice S & P500 para el próximo período.