Prólogo

En este artículo, exploraremos varios aspectos de SVM:
- componente teórico de SVM;
- cómo funciona el algoritmo en muestras que no se pueden dividir en clases linealmente;
- Ejemplo de Python e implementación del algoritmo en la biblioteca SciKit Learn.
En los siguientes artículos, trataré de hablar sobre el componente matemático de este algoritmo.
Como sabe, las tareas de aprendizaje automático se dividen en dos categorías principales: clasificación y regresión. Dependiendo de a cuál de estas tareas nos enfrentamos y qué conjunto de datos tenemos para esta tarea, elegimos qué algoritmo usar.
El método de máquinas de vectores de soporte o SVM (del inglés Support Vector Machines) es un algoritmo lineal utilizado en problemas de clasificación y regresión. Este algoritmo se usa ampliamente en la práctica y puede resolver problemas tanto lineales como no lineales. La esencia de las "máquinas" de los vectores de soporte es simple: el algoritmo crea una línea o hiperplano que divide los datos en clases.
Teoría
La tarea principal del algoritmo es encontrar la línea o hiperplano más correcta, dividiendo los datos en dos clases. SVM es un algoritmo que recibe datos en la entrada y devuelve dicha línea divisoria.
Considere el siguiente ejemplo. Supongamos que tenemos un conjunto de datos y queremos clasificar y separar los cuadrados rojos de los círculos azules (digamos positivo y negativo). El objetivo principal en esta tarea será encontrar la línea "ideal" que separará estas dos clases.
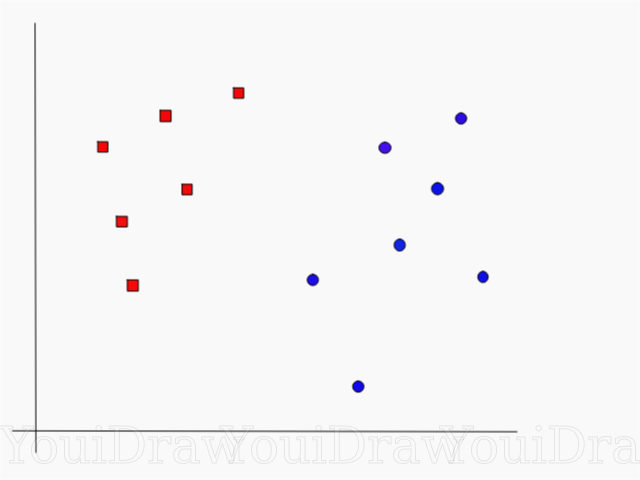
Encuentre la línea perfecta, o hiperplano, que divide el conjunto de datos en clases azul y rojo.
A primera vista, no es tan difícil, ¿verdad?
Pero, como puede ver, no hay una línea única que resuelva ese problema. Podemos recoger un número infinito de líneas que pueden separar estas dos clases. ¿Cómo exactamente SVM encuentra la línea "ideal" y qué es "ideal" en su comprensión?
Eche un vistazo al siguiente ejemplo y piense cuál de las dos líneas (amarilla o verde) separa mejor las dos clases y se ajusta a la descripción de "ideal".
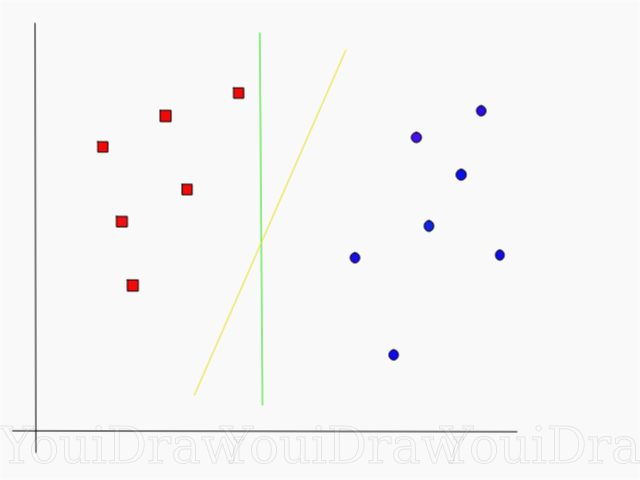
¿Qué línea separa mejor el conjunto de datos en su opinión?
Si elige la línea amarilla, lo felicito: esta es la línea que elegiría el algoritmo. En este ejemplo, podemos entender intuitivamente que la línea amarilla se separa y, en consecuencia, clasifica las dos clases mejor que la verde.
En el caso de la línea verde, se encuentra demasiado cerca de la clase roja. A pesar de que clasificó correctamente todos los objetos del conjunto de datos actual, dicha línea no se generalizará, no se comportará tan bien con un conjunto de datos desconocido. La tarea de encontrar una separación generalizada de dos clases es una de las tareas principales en el aprendizaje automático.
Cómo SVM encuentra la mejor línea
El algoritmo SVM está diseñado de tal manera que busca puntos en el gráfico que se encuentran directamente en la línea de separación más cercana. Estos puntos se denominan vectores de referencia. Luego, el algoritmo calcula la distancia entre los vectores de soporte y el plano divisorio. Esta es la distancia llamada brecha. El objetivo principal del algoritmo es maximizar la distancia de separación. Se considera que el mejor hiperplano es un hiperplano para el cual esta brecha es lo más grande posible.

Bastante simple, ¿verdad? Considere el siguiente ejemplo, con un conjunto de datos más complejo que no se puede dividir linealmente.
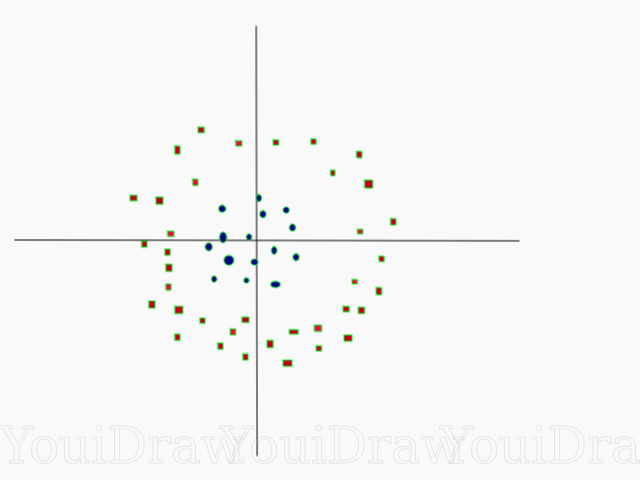
Obviamente, este conjunto de datos no se puede dividir linealmente. No podemos dibujar una línea recta que clasifique estos datos. Pero, este conjunto de datos se puede dividir linealmente agregando una dimensión adicional, que llamaremos eje Z. Imagine que las coordenadas en el eje Z están reguladas por la siguiente restricción:
z=x²+y²
Por lo tanto, la ordenada Z se representa desde el cuadrado de la distancia del punto hasta el comienzo del eje.
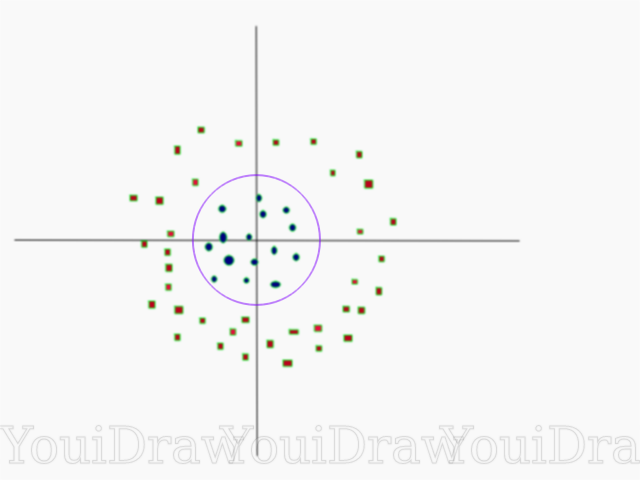
A continuación se muestra una visualización del mismo conjunto de datos en el eje Z.
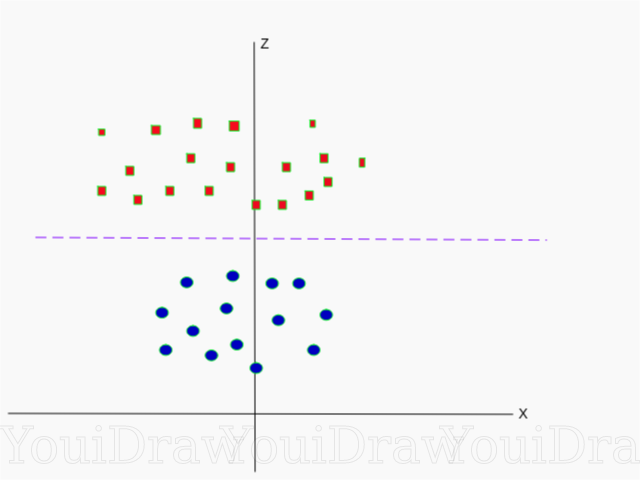
Ahora los datos se pueden dividir linealmente. Suponga que la línea magenta que separa los datos z = k, donde k es una constante. Si
z=x²+y²
entonces
k=x²+y²
- fórmula circular. Por lo tanto, podemos proyectar nuestro divisor lineal, de vuelta al número original de dimensiones de muestra, utilizando esta transformación.
Como resultado, podemos clasificar un conjunto de datos no lineal al agregarle una dimensión adicional y luego devolverlo a su forma original mediante transformación matemática. Sin embargo, no con todos los conjuntos de datos, es igual de fácil acelerar tal transformación. Afortunadamente, la implementación de este algoritmo en la biblioteca sklearn nos resuelve este problema.
Hiperplano
Ahora que nos hemos familiarizado con la lógica del algoritmo, pasamos a la definición formal de un hiperplano
Un hiperplano es un subplano n-1 dimensional en un espacio euclidiano n-dimensional que divide el espacio en dos partes separadas.
Por ejemplo, imagine que nuestra línea se representa como un espacio euclidiano unidimensional (es decir, nuestro conjunto de datos se encuentra en una línea recta). Seleccione un punto en esta línea. Este punto dividirá el conjunto de datos, en nuestro caso la línea, en dos partes. La línea tiene una medida y el punto tiene 0 medidas. Por lo tanto, un punto es un hiperplano de una línea.
Para el conjunto de datos bidimensionales que conocimos anteriormente, la línea divisoria era el mismo hiperplano. En pocas palabras, para un espacio n-dimensional hay un hiperplano n-1 dimensional que divide este espacio en dos partes.
CÓDIGO
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2])
Los puntos se representan como una matriz de X, y las clases a las que pertenecen como una matriz de y.
Ahora entrenaremos a nuestro modelo con esta muestra. Para este ejemplo, configuro el parámetro lineal del "núcleo" del clasificador (núcleo).
from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y)
Predicción de clase de un nuevo objeto.
prediction = clf.predict([[0,6]])
Ajuste de parámetros
Los parámetros son los argumentos que pasa al crear el clasificador. A continuación, proporcioné algunas de las configuraciones SVM personalizadas más importantes:
"C"Este parámetro ayuda a ajustar esa línea fina entre la "suavidad" y la precisión de la clasificación de los objetos en la muestra de entrenamiento. Cuanto mayor sea el valor de "C", más objetos en el conjunto de entrenamiento se clasificarán correctamente.

En este ejemplo, hay varios umbrales de decisión que podemos definir para esta muestra en particular. Preste atención al umbral de decisión directa (presentado en el cuadro como una línea verde). Es bastante simple, y por esta razón, varios objetos se clasificaron incorrectamente. Estos puntos que se han clasificado incorrectamente se denominan valores atípicos en los datos.
También podemos ajustar los parámetros de tal manera que al final obtengamos una línea más curva (umbral de decisión azul claro), que clasificará absolutamente todos los datos de muestra de entrenamiento correctamente. Por supuesto, en este caso, las posibilidades de que nuestro modelo pueda generalizar y mostrar resultados igualmente buenos en nuevos datos son catastróficamente pequeñas. Por lo tanto, si está tratando de lograr la precisión al entrenar el modelo, debe apuntar a algo más uniforme, directo. Cuanto mayor sea el número "C", más enredado estará el hiperplano en su modelo, pero mayor será el número de objetos clasificados correctamente en el conjunto de entrenamiento. Por lo tanto, es importante "torcer" los parámetros del modelo para un conjunto de datos específico con el fin de evitar el reentrenamiento pero, al mismo tiempo, lograr una alta precisión.
GammaEn la documentación oficial, la biblioteca SciKit Learn dice que la gamma determina hasta qué punto cada uno de los elementos del conjunto de datos influye en la determinación de la "línea ideal". Cuanto más baja sea la gama, más elementos, incluso aquellos que están lo suficientemente lejos de la línea divisoria, participan en el proceso de elegir esta misma línea. Si la gamma es alta, entonces el algoritmo "dependerá" solo de aquellos elementos que estén más cerca de la línea misma.
Si el nivel gamma se establece demasiado alto, solo los elementos más cercanos a la línea participarán en el proceso de toma de decisiones sobre la ubicación de la línea. Esto ayudará a ignorar los valores atípicos en los datos. El algoritmo SVM está diseñado para que los puntos ubicados más cerca uno del otro tengan más peso al tomar una decisión. Sin embargo, con la configuración correcta de "C" y "gamma", se puede lograr un resultado óptimo que construirá un hiperplano más lineal que ignore los valores atípicos y, por lo tanto, sea más generalizable.
Conclusión
Espero sinceramente que este artículo le haya ayudado a comprender la esencia del trabajo de SVM o el Método de vector de referencia. Espero de usted cualquier comentario y consejo. En publicaciones posteriores, hablaré sobre el componente matemático de SVM y los problemas de optimización.
Fuentes:
Documentación oficial de SVM en SciKit LearnBlog de TowardsDataScienceSiraj Raval: Máquinas de vectores de soporteIntroducción a Machine Learning Udacity SVM: video del curso GammaWikipedia: SVM