Fuente : Licencia de Wikipedia CC-BY-SA 3.0

Si viaja con frecuencia en transporte público, probablemente se haya encontrado con esta situación:

Te detienes. Está escrito que el autobús sale cada 10 minutos. Tenga en cuenta el tiempo ... Finalmente, después de 11 minutos, llega el autobús y piensa: ¿por qué siempre tengo mala suerte?

En teoría, si los autobuses llegan cada 10 minutos y usted llega a una hora aleatoria, la espera promedio debería ser de aproximadamente 5 minutos. Pero en realidad, los autobuses no llegan a tiempo, por lo que puede esperar más. Resulta que, con algunas suposiciones razonables, uno puede llegar a una conclusión sorprendente:

Cuando espere un autobús que llega en promedio cada 10 minutos, su tiempo de espera promedio será de 10 minutos.

Esto es lo que a veces se llama la paradoja del tiempo de espera .

Tuve una idea antes, y siempre me pregunté si esto es realmente cierto ... ¿cuánto corresponden esas "suposiciones razonables" a la realidad? En este artículo, examinamos la paradoja de la latencia en términos de modelos y argumentos probabilísticos, y luego echamos un vistazo a algunos de los datos reales del autobús en Seattle para (con suerte) resolver la paradoja de una vez por todas.

Inspección paradoja

Si los autobuses llegan exactamente cada diez minutos, el tiempo promedio de espera será de 5 minutos. Uno puede entender fácilmente por qué agregar variaciones al intervalo entre los autobuses aumenta el tiempo de espera promedio.

La paradoja del tiempo de espera es un caso especial de un fenómeno más general: la paradoja de la inspección , que se discute en detalle en el artículo sensible de Allen Downey, "La paradoja de la inspección en todas partes a nuestro alrededor" .

En resumen, la paradoja de la inspección surge cuando la probabilidad de observar una cantidad está relacionada con la cantidad observada. Allen da un ejemplo de cuestionar a los estudiantes universitarios sobre el tamaño promedio de sus clases. Aunque la escuela habla sinceramente del número promedio de 30 estudiantes por grupo, el tamaño promedio del grupo desde el punto de vista de los estudiantes es mucho mayor. La razón es que en clases grandes (naturalmente) hay más estudiantes, lo que se revela durante su encuesta.

En el caso de un horario de autobús con un intervalo de 10 minutos declarado, a veces el intervalo entre llegadas es mayor de 10 minutos y, a veces, más corto. Y si se detiene en un momento aleatorio, entonces es más probable que encuentre un intervalo más largo que uno más corto. Y, por lo tanto, es lógico que el intervalo de tiempo promedio entre intervalos de espera sea más largo que el intervalo de tiempo promedio entre buses, porque los intervalos más largos son más comunes en la muestra.

Pero la paradoja de la latencia hace una declaración más fuerte: si el espaciado promedio del bus es

$N$ minutos, el tiempo de espera promedio para pasajeros es

$2N$ minutos ¿Podría ser esto cierto?

Simulación de latencia

Para convencernos de lo razonable de esto, primero simulamos el flujo de autobuses que llegan en un promedio de 10 minutos. Para mayor precisión, tome una muestra grande: un millón de autobuses (o aproximadamente 19 años de tráfico de 10 minutos las 24 horas):

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N))

Verifique que el intervalo promedio esté cerca de

$\ tau = 10$ :

 intervals = np.diff(bus_arrival_times) intervals.mean()

9.9999879601518398

Ahora podemos simular la llegada de una gran cantidad de pasajeros a una parada de autobús durante este período de tiempo y calcular el tiempo de espera que cada uno de ellos experimenta. Encapsule el código en una función para su uso posterior:

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times

Luego simulamos el tiempo de espera y calculamos el promedio:

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean()

10.001584206227317

El tiempo de espera promedio es cercano a 10 minutos, como predijo la paradoja.

Profundizando: probabilidades y procesos de Poisson

¿Cómo simular tal situación?

De hecho, este es un ejemplo de una paradoja de inspección, donde la probabilidad de observar un valor está relacionada con el valor mismo. Denote por

$p (T)$ espaciamiento

$T$ entre los autobuses cuando llegan a la parada de autobús. En dicho registro, el valor esperado de la hora de llegada será:

$E [T] = \ int_0 ^ \ infty T ~ p (T) ~ dT$

En la simulación anterior, seleccionamos

$E [T] = \ tau = 10$ minutos

Cuando un pasajero llega a una parada de autobús en cualquier momento, la probabilidad de tiempo de espera dependerá no solo de

$p (T)$ pero también de

$T$ : cuanto mayor es el intervalo, más pasajeros hay en él.

Por lo tanto, podemos escribir la distribución del tiempo de llegada desde el punto de vista de los pasajeros:

$p_ {exp} (T) \ propto T ~ p (T)$

La constante de proporcionalidad se deriva de la normalización de la distribución:

$p_ {exp} (T) = \ frac {T ~ p (T)} {\ int_0 ^ \ infty T ~ p (T) ~ dT}$

Se simplifica a

$p_ {exp} (T) = \ frac {T ~ p (T)} {E [T]}$

Entonces el tiempo de espera

$E [W]$ será la mitad del intervalo esperado para los pasajeros, por lo que podemos registrar

$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T ~ p_ {exp} (T) ~ dT$

que se puede reescribir de una manera más comprensible:

$E [W] = \ frac {E [T ^ 2]} {2E [T]}$

y ahora solo queda elegir un formulario para

$p (T)$ y calcular las integrales.

La elección de p (T)

Habiendo recibido un modelo formal, ¿cuál es una distribución razonable para

$p (T)$ ? Dibujaremos una imagen de distribución

$p (T)$ dentro de nuestras llegadas simuladas trazando un histograma de los intervalos entre llegadas:

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density');

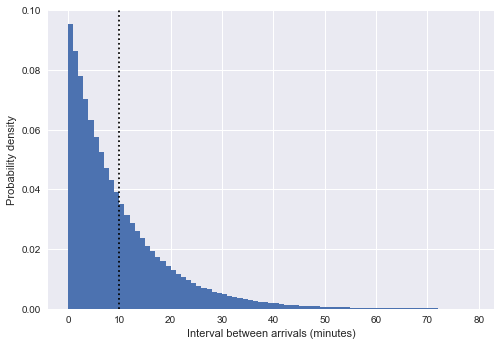
Aquí, la línea discontinua vertical muestra un intervalo promedio de aproximadamente 10 minutos. Esto es muy similar a una distribución exponencial, y no por accidente: nuestra simulación del tiempo de llegada del autobús en forma de números aleatorios uniformes está muy cerca del proceso de Poisson , y para tal proceso, la distribución de intervalos es exponencial.

(Nota: en nuestro caso, esto es solo un exponente aproximado; de hecho, los intervalos

$T$ entre

$N$ puntos uniformemente seleccionados dentro de un lapso de tiempo

$N \ tau$ coincidir con la distribución beta

$T / (N \ tau) \ sim \ mathrm {Beta} [1, N]$ que está en el gran límite

$N$ acercándose

$T \ sim \ mathrm {Exp} [1 / \ tau]$ . Para obtener más información, puede leer, por ejemplo, una publicación en StackExchange o este hilo en Twitter ).

La distribución exponencial de los intervalos implica que el tiempo de llegada sigue el proceso de Poisson. Para verificar este razonamiento, verificamos la presencia de otra propiedad del proceso de Poisson: que el número de llegadas durante un período de tiempo fijo es una distribución de Poisson. Para hacer esto, dividimos las llegadas simuladas en bloques de tiempo:

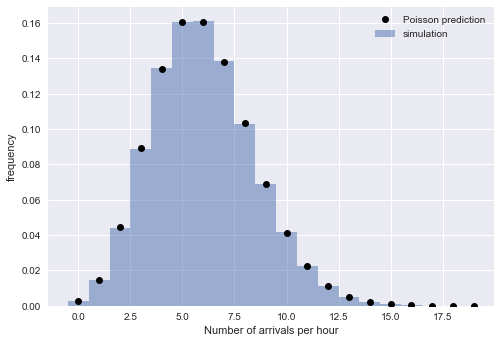
 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend();

La estrecha correspondencia de valores empíricos y teóricos nos convence de la exactitud de nuestra interpretación: para grandes

$N$ El tiempo de llegada simulado está bien descrito por el proceso de Poisson, que implica intervalos distribuidos exponencialmente.

Esto significa que la distribución de probabilidad se puede escribir:

$p (T) = \ frac {1} {\ tau} e ^ {- T / \ tau}$

Si sustituimos el resultado en la fórmula anterior, encontraremos el tiempo de espera promedio para los pasajeros en la parada:

$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2 ~ e ^ {- T / \ tau}} {2 \ int_0 ^ \ infty T ~ e ^ {- T / \ tau}} = \ frac {2 \ tau ^ 3} {2 (\ tau ^ 2)} = \ tau$

Para vuelos con llegadas a través del proceso de Poisson, el tiempo de espera esperado es idéntico al intervalo promedio entre llegadas.

Este problema se puede discutir de la siguiente manera: el proceso de Poisson es un proceso sin memoria , es decir, el historial de eventos no tiene nada que ver con el tiempo esperado del próximo evento. Por lo tanto, al llegar a una parada de autobús, el tiempo de espera promedio para un autobús es siempre el mismo: en nuestro caso, son 10 minutos, ¡independientemente de cuánto tiempo haya pasado desde el autobús anterior! No importa cuánto tiempo haya estado esperando: el tiempo esperado para el próximo autobús siempre es exactamente 10 minutos: en el proceso de Poisson no obtiene un "crédito" por el tiempo que pasó esperando.

Tiempo de espera de realidad

Lo anterior es bueno si las llegadas reales de autobuses se describen realmente por el proceso de Poisson, pero ¿es así?

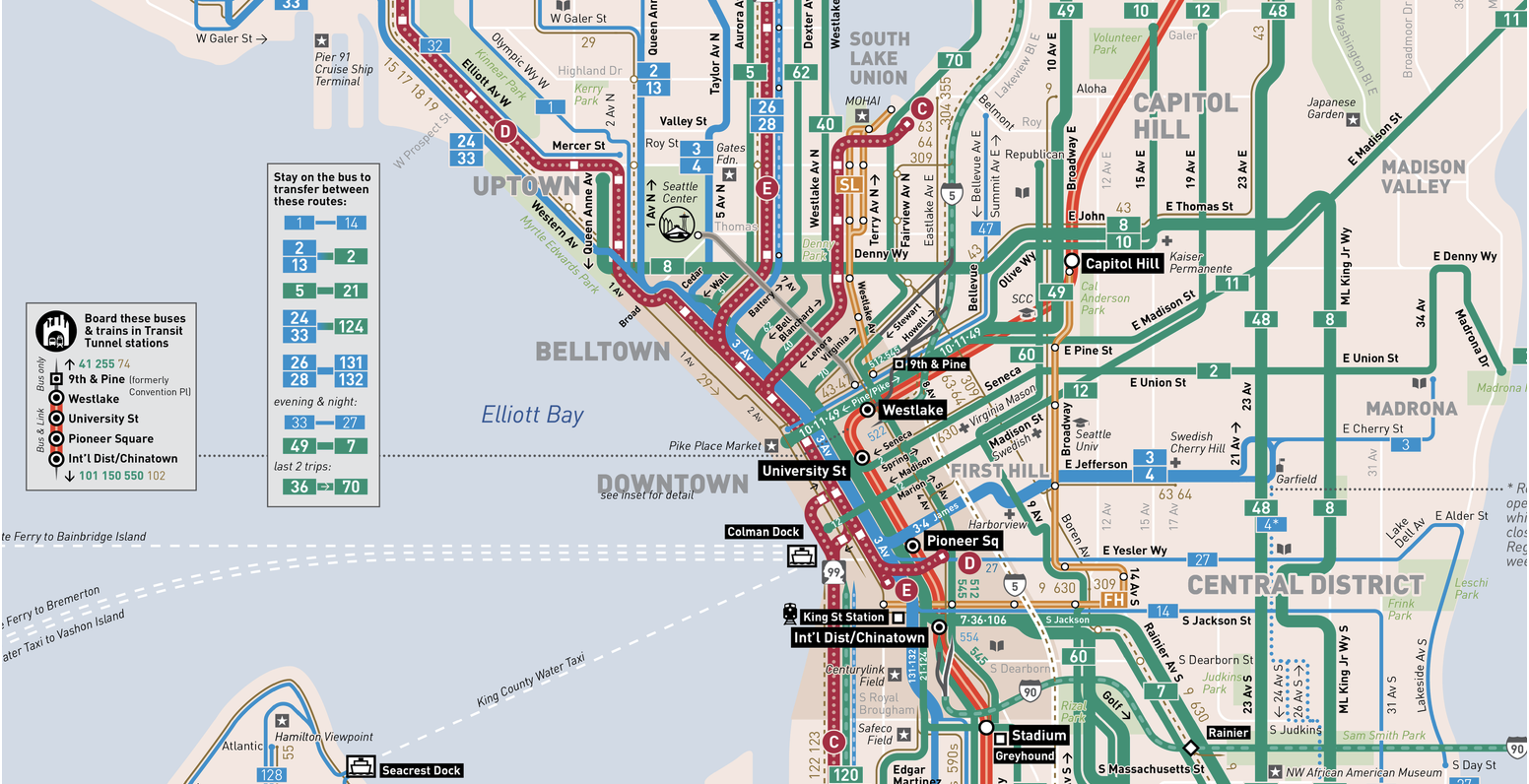Fuente: Esquema de transporte público de Seattle

Tratemos de determinar cómo la paradoja del tiempo de espera es consistente con la realidad. Para hacer esto, examinaremos algunos de los datos disponibles para descargar aquí: arrival_times.csv (archivo CSV de 3 MB). El conjunto de datos contiene los tiempos de llegada planificados y reales para los autobuses RapidRide C, D y E en la parada de autobús 3rd & Pike en el centro de Seattle. Los datos se registraron en el segundo trimestre de 2016 (¡muchas gracias a Mark Hallenback del Centro de Transporte del Estado de Washington por este archivo!).

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head()

	OPD_DATE	VEHÍCULO_ID	RTE	DIR	ID_TRIP	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0 0	2016-03-26	6201	673	S	30908177	431	3 ° AVE Y PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	S	30908033	431	3 ° AVE Y PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3 ° AVE Y PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3 ° AVE Y PIKE ST (431)	19:04:57	19:01:49
4 4	2016-03-26	6201	673	S	30908252	431	3 ° AVE Y PIKE ST (431)	16:42:57	16:42:39

Elegí los datos de RapidRide, incluso porque durante la mayor parte del día los autobuses circulan a intervalos regulares de 10-15 minutos, sin mencionar el hecho de que soy un pasajero frecuente de la ruta C.

Limpieza de datos

Primero, haremos un poco de limpieza de datos para convertirlo en una vista conveniente:

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head()

	Ruta	Dirección	Graph	Hecho llegada	Tardanza (min)
0 0	C	sur	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1	C	sur	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	sur	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	sur	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4 4	C	sur	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

¿Qué tan tarde son los autobuses?

Hay seis conjuntos de datos en esta tabla: direcciones norte y sur para cada ruta C, D y E. Para tener una idea de sus características, construyamos un histograma del tiempo real menos el tiempo de llegada planificado para cada uno de estos seis:

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses');

Es lógico suponer que los autobuses están más cerca del horario al comienzo de la ruta y se desvían más hacia el final. Los datos confirman esto: nuestra parada en la ruta sur C, así como en el norte D y E está cerca del comienzo de la ruta, y en la dirección opuesta, no lejos del destino final.

Intervalos programados y observados

Eche un vistazo a los intervalos de autobús observados y planificados para estas seis rutas. Comencemos con la función groupby en Pandas para calcular estos intervalos:

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses');

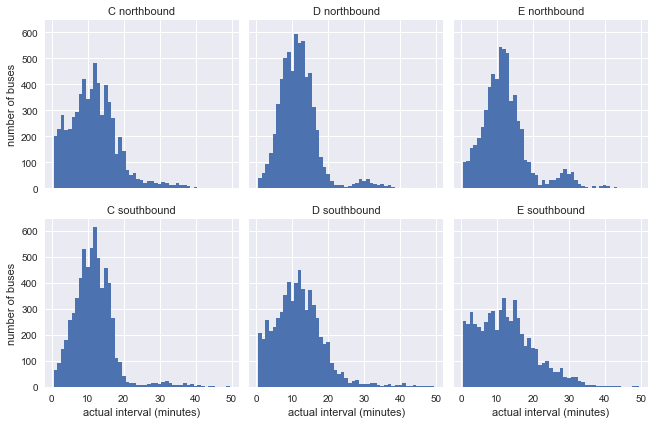
Ya es evidente que los resultados no son muy similares a la distribución exponencial de nuestro modelo, pero esto aún no dice nada: las distribuciones pueden verse afectadas por intervalos inconsistentes en el gráfico.

Repitamos la construcción de diagramas, tomando los intervalos de llegada planeados, en lugar de los observados:

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency');

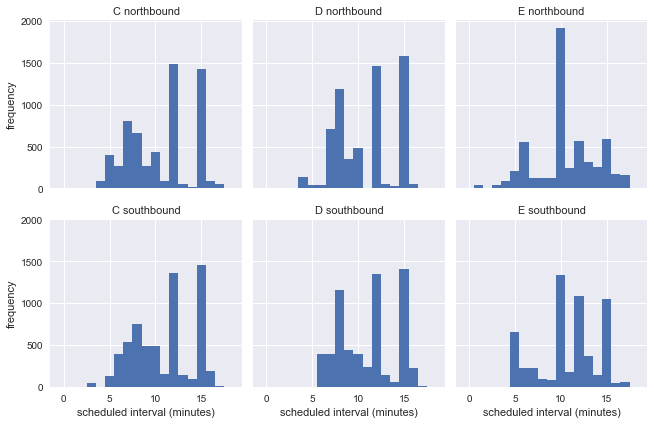
Esto muestra que durante la semana los autobuses circulan a diferentes intervalos, por lo que no podemos estimar la precisión de la paradoja del tiempo de espera utilizando información real de la parada del autobús.

Construyendo horarios uniformes

Aunque el horario oficial no proporciona intervalos uniformes, hay varios intervalos de tiempo específicos con una gran cantidad de autobuses: por ejemplo, casi 2000 autobuses de la ruta E hacia el norte con un intervalo planificado de 10 minutos. Para averiguar si la paradoja de la latencia es aplicable, agrupemos los datos en rutas, direcciones y el intervalo planificado, y luego volvamos a apilarlos como si hubieran sucedido secuencialmente. Esto debería preservar todas las características relevantes de los datos de origen, al tiempo que facilita la comparación directa con las predicciones de la paradoja de la latencia.

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head()

	Ruta	Dirección	Horario	Hecho llegada	Tardanza (min)	Hecho intervalo	Intervalo programado
0 0	C	norte	10,0	12.400000	2,400,000	NaN	10,0
1	C	norte	20,0	27.150000	7.150000	0.183333	10,0
2	C	norte	30,0	26.966667	-3.033333	14.566667	10,0
3	C	norte	40,0	35.516667	-4,483333	8.366667	10,0
4 4	C	norte	50,0	53,583333	3.583333	18.066667	10,0

En los datos borrados, puede hacer un gráfico de la distribución de la apariencia real de los autobuses a lo largo de cada ruta y dirección con una frecuencia de llegada:

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)

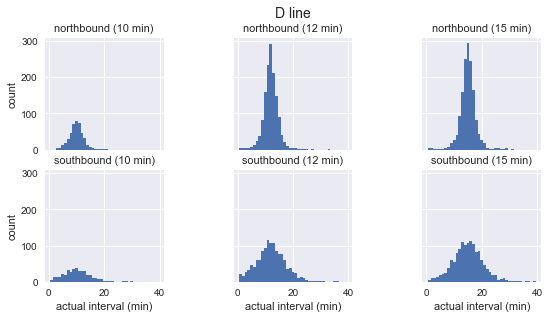
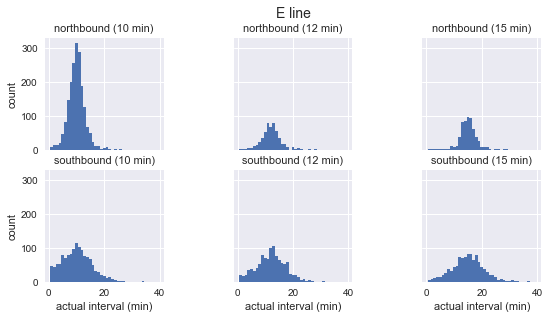
Vemos que para cada ruta la distribución de los intervalos observados es casi gaussiana. Pico cerca del intervalo planificado y tiene una desviación estándar que es menor al comienzo de la ruta (sur para C, norte para D / E) y más al final. Incluso a simple vista, los intervalos de llegada reales definitivamente no corresponden a la distribución exponencial, que es el supuesto principal en el que se basa la paradoja del tiempo de espera.

Podemos tomar la función de simulación del tiempo de espera que utilizamos anteriormente para encontrar el tiempo de espera promedio para cada ruta, dirección y horario del autobús:

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std()))

  Dirección de ruta Intervalo programado
 C norte 10.0 7.8 +/- 12.5
                       12.0 7.4 +/- 5.7
                       15.0 8.8 +/- 6.4
          sur 10.0 6.2 +/- 6.3
                       12.0 6.8 +/- 5.2
                       15.0 8.4 +/- 7.3
 D norte 10.0 6.1 +/- 7.1
                       12.0 6.5 +/- 4.6
                       15.0 7.9 +/- 5.3
          sur 10.0 6.7 +/- 5.3
                       12.0 7.5 +/- 5.9
                       15.0 8.8 +/- 6.5
 E norte 10.0 5.5 +/- 3.7
                       12.0 6.5 +/- 4.3
                       15.0 7.9 +/- 4.9
          sur 10.0 6.8 +/- 5.6
                       12.0 7.3 +/- 5.2
                       15.0 8.7 +/- 6.0
 Nombre: actual, dtype: objeto

El tiempo de espera promedio, quizás uno o dos minutos, es más de la mitad del intervalo planificado, pero no es igual al intervalo planificado, como implica la paradoja del tiempo de espera. En otras palabras, se confirma la paradoja de la inspección, pero la paradoja del tiempo de espera no es cierta.

Conclusión

La paradoja de la latencia fue un punto de partida interesante para una discusión que incluyó modelado, teoría de la probabilidad y comparación de supuestos estadísticos con la realidad. Aunque hemos confirmado que en el mundo real, las rutas de autobuses obedecen a algún tipo de paradoja de inspección, el análisis anterior muestra de manera bastante convincente: la suposición principal que subyace en la paradoja del tiempo de espera, que la llegada de autobuses sigue las estadísticas del proceso de Poisson, no está justificada.

Mirando hacia atrás, esto no es sorprendente: el proceso de Poisson es un proceso sin memoria, que supone que la probabilidad de llegada es completamente independiente del tiempo desde el momento de la llegada anterior. De hecho, un sistema de transporte público bien administrado tiene horarios especialmente estructurados para evitar este comportamiento: los autobuses no comienzan sus rutas en momentos aleatorios durante el día, sino que comienzan de acuerdo con el horario elegido para el transporte más eficiente de pasajeros.

La lección más importante es tener cuidado con las suposiciones que haga sobre cualquier tarea de análisis de datos. A veces, el proceso de Poisson es una buena descripción de los datos del tiempo de llegada. Pero el hecho de que un tipo de datos suene como otro tipo de datos no significa que los supuestos permitidos para uno sean necesariamente válidos para el otro. A menudo, las suposiciones que parecen correctas pueden llevar a conclusiones que no son ciertas.

La paradoja del tiempo de espera, o ¿por qué mi autobús siempre llega tarde?